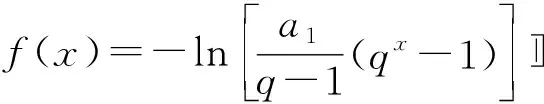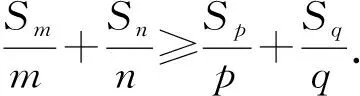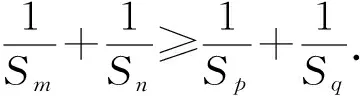由省賽題談數列“凸性”的簡單應用*
●
(嚴州中學新安江校區,浙江 建德 311600)
2018年浙江省高中數學競賽已經落幕,縱觀全卷,難度較2017年明顯下降.筆者對第13題的數列不等式題產生了興趣.
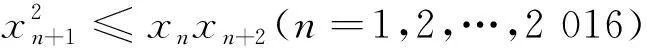
(2018年浙江省高中數學競賽試題第13題)
1 證法探究
本題的證明并不難,參考答案提供的是反證法,證法如下:

1)若x1 009,x1 010同為正數,由xn,xn+2同號可知:x1,x2,…,x2 018同為正.
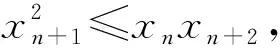
從而
即
x1 009x1 010≤x1 011x1 008,
于是
x1 011x1 008>1.
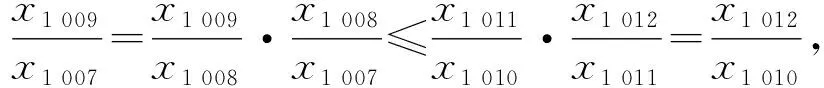
即
x1 007x1 012>1,
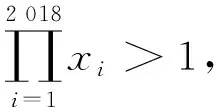
2)若x1 009,x1 010同為負數,由xn,xn+2同號可知:x1,x2,…,x2 018都為負數,故
即
由情形1)知不等式成立.
賽后跟學生交流,發現學生的想法也很不錯,筆者略作整理,得到如下兩種證法:

1)若x1 009·x1 010<0,則結論顯然成立.
2)若x1 009·x1 010>0,則x1,x2,…,x2 018全同號,不妨設全為正數(若為負數,則可用-xi代替xi,不影響結果).
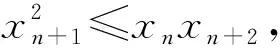
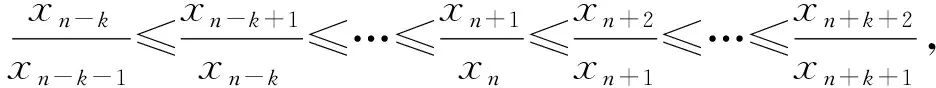
從而xn+k+1xn-k≤xn+k+2xn-k-1(其中0≤k≤n).
取n=1 009,得
x1 009x1 010≤x1 008x1 011≤x1 007x1 012≤…≤x1x2 018,
從而
即
x1 009x1 010≤1.

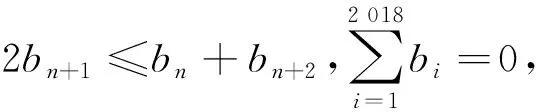
bn+2-bn+1≥bn+1-bn,
即數列{bn+1-bn}單調不減,則
其中k=1,2,…,1 009,即
b1 009+b1 010≤bk+b2 019-k,
對k求和得
即
故
b1 009+b1 010≤0.
2 題源探究
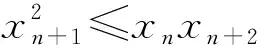
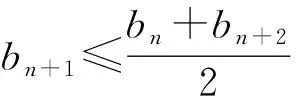
定義若實數列{an}滿足ak-1+ak+1≥2ak(其中k=1,2,…),則稱數列{an}為下凸數列,簡稱凸數列,當且僅當{an}為等差數列時,等號對所有k∈N*成立.
由定義可知,對于實數列{an},若Δan=an+1-an(其中n=0,1,2,…),則數列{an}為凸數列的充要條件是數列{Δan}為單調不減數列.
因為等差數列是特殊的凸數列,那么一般的凸數列是否具備類似等差數列的性質呢?從證法3可得到凸數列的一個重要性質:
性質1若數列{an}為凸數列,滿足1≤m 證明因為n>q≥p>m≥1,又{an+1-an}單調不減,所以 即 an-aq≥ap-am, 結論成立. 此外還有一些類似等差數列的性質,在此不再一一例舉.在一些大型的考試中,也屢見凸數列的“身影”,下面試舉兩例來說明. 真題1設實數x1,x2,…,x30滿足x1=1,x30=88,2xn+1≤xn+xn+2(其中n=1,2,…,28),求x10的最大可能值. (2018年中國女子數學奧林匹克浙江省選拔試題第3題) 解由題意知數列{xn}為凸數列,故{xn+1-xn}是單調不減數列,令Δxn=xn+1-xn,則 Δx1≤Δx2≤…≤Δx29, 且 Δx1+Δx2+…+Δx29=87, 即 Δx1+Δx2+…+Δx9≤27, 故 x10=x1+(Δx1+Δx2+…+Δx9)≤28. (2008年上海市春季數學高考試題第21題) 證明易知 bn=(1,an+1-an)·(0,1)=an+1-an, bn+1=an+2-an+1, 因為bn+1>bn,所以 an+2-an+1>an+1-an, 即數列{an}為“下凸數列”.要證 即證 aq-ap>an-am. 由于q-p=n-m,將所證不等式改寫為 由{an+1-an}的遞增性,知結論顯然成立. 在研究完兩個真題后,筆者感到意猶未盡,在翻閱文獻時,發現在文獻[1]中給出等差、等比數列的一些統一性質,其論證過程比較麻煩.經過嘗試,筆者發現若利用凸數列的性質來證明,可以極大地簡化證明過程. 性質2正項等差數列或等比數列{an}中,當m+n=p+q,m 證明1)若{an}為等比數列,則顯然有 aman=apaq. 2)若{an}為正項等差數列,設an=pn+q(其中p>0),則令bn=-lnan,考慮 f(x)=-ln (px+q)(其中x>0), p,q為常數,則 從而f(x)為凸函數,故數列{bn}是凸數列,則 bm+bn≥bp+bq, 即 -lnam-lnan≥-lnap-lnaq, 亦即 aman≤apaq. 性質3正項等差數列或等比數列{an}中,當m+n=p+q,m 證明1)若{an}為等差數列,則顯然有 am+an=ap+aq. 2)若{an}為正項等比數列,設an=a1qn-1(其中a1>0,q>0),顯然數列{a1qn-1}是凸數列,則am+an≥ap+aq. 性質4設正項等差數列或等比數列的前n項和為Sn,則當m+n=p+q,m 從而f(x)為凸函數,故數列{-lnSn}是凸數列,于是 -lnSm-lnSn≥-lnSp-lnSq, 即 SmSn≤SpSq. 則 從而f(x)為凸函數,故{-lnSn}是凸數列,即 -lnSm-lnSn≥-lnSp-lnSq, 于是 SmSn≤SpSq. 性質5設正項等差數列或遞增等比數列的前n項和為Sn,則當m+n=p+q,m 2)若{an}為正項等比數列且q=1,則顯然有 Sm+Sn=Sp+Sq. 此外通過性質2~5的證明,筆者還發現了與凸數列有關的等差、等比的其他一些性質: 由于性質6~8的證明過程和性質1~5類似,故在此不再贅述.在性質2~8中對于等差、等比數列還有一定的限制,那么對于更一般的等差、等比數列,上述性質還成立嗎?由于筆者能力有限,未能給出結果,請同行幫忙證明.3 用“凸性”研究真題
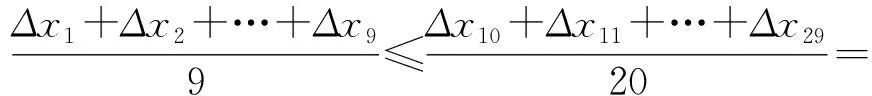
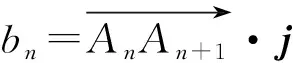
4 由“凸性”研究等差、等比數列的統一性質