一題多維“細”探究 零點反思“化”歸根*
——一道高考函數壓軸題的解法探究與反思

●

(天水市第一中學,甘肅 天水 741000)

1 試題呈現

題目已知函數f(x)=ex-ax2．

1)若a=1，證明：當x≥0時，f(x)≥1；

2)若f(x)在(0,+∞)上只有一個零點，求a．

(2018年全國數學高考卷Ⅱ理科試題第21題)

2 表征解讀

本題條件只是一個含e的函數解析式，蘊藏著一個參數a和兩類基本函數(指數函數和二次函數)，第1)小題屬于不等式的證明；第2)小題通過零點求參數，結構與形式凸顯了數學之美：簡單、簡潔、簡捷.結構如此經典之美的數學題，就會激發學生對解法作深入研究的動力.

3 解法探究

3.1 第1)小題剖析

視角1函數角度.

從證明的目標“當x≥0時，f(x)≥1”成立入手，將目標直譯為在條件“x≥0”下，不等式“f(x)min≥1”成立即可.

解法1若a=1，則函數f(x)=ex-x2，求導可得f′(x)=ex-2x，此時不好判斷該導數f′(x)的正負，故設g(x)=ex-2x，則

g′(x)=ex-2，

令g′(x)=0，解得x=ln 2，列表1.

表1 導函數對應值

從表1可知g(x)≥g(ln 2)=2-2ln 2>0，從而f′(x)>0，因此函數f(x)在區間[0，+∞)上單調遞增，故f(x)>f(0)=1.

視角2等價轉化角度.

對所要證明的不等式，如果直接不好證明，可以先進行等價變形，然后再證明其成立即可.

解法2當a=1時，不等式f(x)≥1等價變形為(x2+1)e-x-1≤0．設函數g(x)=(x2+1)e-x-1，求導可得

g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x．

當x≠1時，g′(x)<0，函數g(x)在區間(0,+∞)上單調遞減．而g(0)=0，故當x≥0時，g(x)≤0，即f(x)≥1．

易知在[0,+∞)上g′(x)≥0恒成立，因此g(x)在x=0處取到最小值，即g(x)≥g(0)=1,故不等式f(x)≥1成立．

評注本題是一道常規不等式的證明題，既考查了學生對簡單問題的轉化能力，又考查了數學思想.學生在考試中容易從函數角度思考，思路如果清晰，就能夠很快解決問題.若對此題進行深入研究，就會發現此題中對函數f(x)直接求導，不容易確定函數的走勢，需要靈活處理：等價變形為

(x2+1)e-x-1≤0,

或

或對導函數f′(x)=ex-2x二次求導才能夠解決問題，有利于對導數與函數關系的深刻理解.

3.2 第2)小題剖析

本小題是零點問題，屬于高考的熱點問題，求解時常將零點問題轉化為方程解的問題，或轉化為兩個新函數的圖像交點問題.一旦參數參與其中，問題就會變得復雜一些.

視角1直接分離參數.

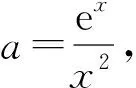
令h′(x)=0，解得x=2，列表2如下：

表2 導函數對應值

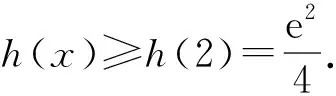
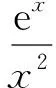
視角2直接對參數討論.

上述視角1的直接分離參數是常用方法，但有時也可以對參數直接進行分類討論.本題中函數f(x)的導函數f′(x)的正負無法直接判斷，因此需要對導函數f′(x)進行二次求導，當x∈(0,+∞)時，對參數a進行分類討論.

解法2對函數f(x)=ex-ax2(其中x>0)求導可得f′(x)=ex-2ax，設g(x)=ex-2ax，對函數g(x)求導可得g′(x)=ex-2a.

由于x∈(0,+∞)，下面對參數a進行分類討論：

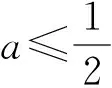
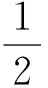
此時需要討論1-ln 2a的正負：

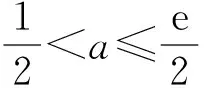
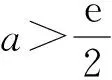
聯立

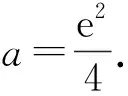
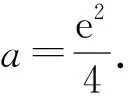
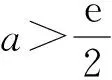
視角3直線與曲線相切.

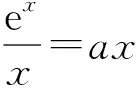
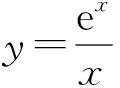
從而

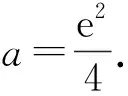
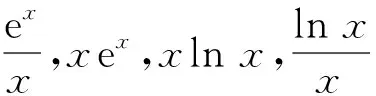
視角4兩條曲線相切.

借助常見的函數y=ex和y=ax2(其中a>1)的圖像與性質，將“方程ex-ax2=0只有一個根”，變形為“方程ex=ax2只有一個根”，等價轉化為“函數y=ex的圖像和函數y=ax2(其中a>1)的圖像相切”，從而求得a的值.

解法4f(x)=ex-ax2=0變形得ax2=ex.設函數g(x)=ex，h(x)=ax2,易知g(x)在(0,+∞)上單調遞增.

由第1)小題ex>x2可知，參數a一定滿足a>1.又函數y=ax2(其中a>1)在(0,+∞)上單調遞增.結合題意“方程ex-ax2=0只有一個根”，即“方程ex=ax2只有一個根”，下面討論的對象是指數函數y=ex與二次函數y=ax2的交點問題.

結合題設條件，易知“函數y=ex的圖像”和“函數y=ax2(其中a>1)的圖像”具有上升的特征，兩條曲線只有相切時才能夠符合題意.也就是兩個函數的圖像只有一個公共切點(有一條共同的切線)，不妨設該切點M的坐標為(m,em).易知第一個關系式

em=am2(其中a>1,m>0),

兩條曲線在公共點M處的斜率相等，可得第二個關系式

em=2am(其中a>1,m>0).

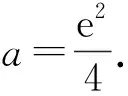
評注兩條曲線相切的研究形式多樣，曲線的走勢多變，研究其相切的難度比較大.

視角5先等價轉化，再分類.

本題中的“f(x)在(0,+∞)上只有一個零點”等價于“函數h(x)=1-ax2e-x在(0,+∞)上只有一個零點”，再討論函數h(x)的單調性，結合h(x)的最小值分類討論得到a的值.

解法5設函數h(x)=1-ax2e-x,則f(x)在(0,+∞)上只有一個零點當且僅當h(x)在(0,+∞)上只有一個零點．

1)當a≤0時，h(x)>0，h(x)沒有零點.

2)當a>0時，h′(x)=ax(x-2)e-x．

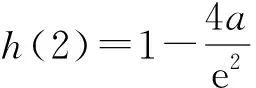
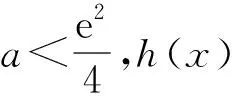
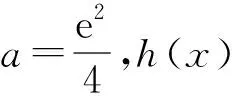
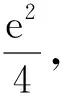
故h(x)在(2,4a)上有一個零點，因此h(x)在(0,+∞)上有兩個零點．

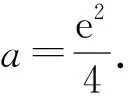
評注對參數a分類討論，需要判斷各種情況下得到的參數a的范圍是否符合題意，把各種符合題意的范圍取并集，即為參數a的取值范圍.但有一些不等式恒成立問題需要對自變量x進行分類討論，對各種情況下的a的取值范圍取交集，即為參數a的取值范圍.

4 解后反思

4.1 審題立足數學概念，思悟規律回歸教材

函數零點(或方程根的個數)問題是近幾年高考的熱點.在函數的定義域內，探究函數單調性和極值，需要弄清函數的走勢，以及函數的零點個數或零點近似值范圍.本題第2)小題涉及“函數只有一個零點”，強調了“零點”的個數和唯一性等特征下，“確定”對應的參數a的值.

第2)小題解法剖析中的幾種思維視角，不外乎分離參數、分離函數和等價轉化等三大審題、解題策略.本題的分離參數只有視角1，分離函數有視角3和視角4，等價轉化有視角2和視角5，不論哪一種策略，都會立足數學中的函數、導數等概念，如視角2中，對導函數又采用了二次求導，此時一定要切記“導函數正負決定了原函數的增減”這一根本點，在此基礎上討論極值問題或最值問題就會顯得自然和舒坦.

4.2 挖掘審題視角，深究通性通法

高度重視導數、函數之間的關系(解析式、圖像等)，掌握函數走勢(單調性、周期性、對稱性等)的確定方法與技巧，既可以提高解題效率，又可以提升學生審題的自信心.近幾年數學高考常常以函數為載體，在導數、方程、不等式等知識點的交匯處命制壓軸題，要求學生要重視運算能力和運算速度的提高，特別是涉及參數取值范圍的確定，平時訓練一定要注重算理、算法和正確地分類，否則轉化方式方法中的邏輯性就會混亂，簡捷的思維就難以形成.

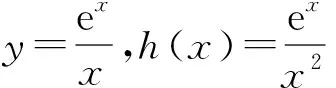
4.3 注重數學思想方法，積淀解題經驗

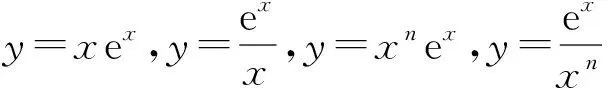
總之，還要掌握一些典型函數問題的解題策略：判斷函數的單調性、求函數的極值(或最值)、證明不等式、討論函數的零點或函數的圖像等審題、解題常用的方法技巧，力爭做到討論不遺漏、分析要全面、計算要精準、思路要簡捷，從而提高借用數學思想方法確定最優解題方法的選擇能力,縮短解題長度和提升解題能力，有利于學生思維層次的提升，同時也積淀了多方位、多視角探究解題的經驗，更加有利于學生數學核心素養的養成與提升.