注重基礎 突出通法 聚焦素養*
——2018年浙江省高考數學試卷評析

●

(學軍中學，浙江 杭州 310012)

2018年是浙江省實施高考改革后的第二年，又是實行文理合卷的第二年，針對“2018年浙江省數學高考試卷的特點，命題有哪些不足，對高中數學教學有何導向”，筆者談談自己的認識，以求拋磚引玉．

1 命題的特點

試卷嚴格遵循《普通高中數學課程標準(2017年)》(以下簡稱《課程標準》)、《浙江省普通高中學科教學指導意見(數學)》及《2018年浙江省普通高考考試說明(數學)》，系統、全面地考查了高中數學的基礎知識、基本技能、基本方法和基本數學思想．依然保持浙江數學試卷的鮮明特色，同時克服試題的模式化，難度較2017年有所下降，受到了考生、教師的普遍認同．有利于高校選拔人才，有利于引導高中數學教學，可謂“注重基礎、突出通法、聚焦素養”，主要體現了以下3個特點：

1．1 層次分明，難度降低

充分考慮到文理合卷的特點，2018年命題依然采用2017年的命題策略——文科韻味、理科深度，與2017年試卷相比，再次增加了簡單試題的數量，如選擇題第1～4題和填空題第11～14題，這些題為課本練習題的難度，起點較低，只要仔細做，就能做對；選擇題、填空題最后一題及最后兩個解答題為全卷壓軸，控制高分人數；設置中檔題和分步設問，這些題接近課本習題或復習參考題難度，讓基礎薄弱的學生爭取及格成為可能，同時使一些優秀學生脫穎而出．從閱卷信息反饋看，全省平均分比2017年提高了5分，但高分人數比2017年減少了，基本符合命題專家的預期．

1.2 突出通法，注重本質

數學教學總是從概念開始，由此引出定理、公式等相關運算，所得的解題方法即是所謂的“通性通法”，這是教學中首先應該強調的“一般法則”.2018年試卷充分考慮了解題方法的大眾化與常規化，不在冷僻的技巧上設置問題，努力貼近學生，在通性通法上下功夫，試題熟悉而不脫俗，材料背景熟悉，設問方式常規，解題方法基本，凸顯數學本質，在考基礎、通性、通法上體現得淋漓盡致.

例1已知四棱錐S-ABCD的底面是正方形，側棱長均相等，E是線段AB上的點(不含端點)．設SE與BC所成的角為θ1，SE與平面ABCD所成的角為θ2，二面角S-AB-C的平面角為θ3，則

( )

A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1

C.θ1≤θ3≤θ2D.θ2≤θ3≤θ1

(2018年浙江省數學高考試題第8題)

此題將空間3個角植入特定的四棱錐中，比較3個角的大小，解答此題只需線線角、線面角、面面角的概念清晰，作出3個角，轉化為比較3個角正切值的大小，便可得出結論．

試卷對函數與方程思想、分類討論思想、數形結合思想、轉化思想等進行了全面的考查.試題呈現“簡約而不簡單”，入口寬，解題途徑比較多.選擇的切入點不同，解題過程的簡捷程度也不同，可以檢測不同層次學生的思維水平．如：

( )

(2018年浙江省數學高考試題第9題)

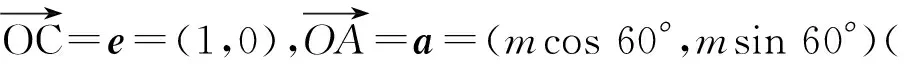
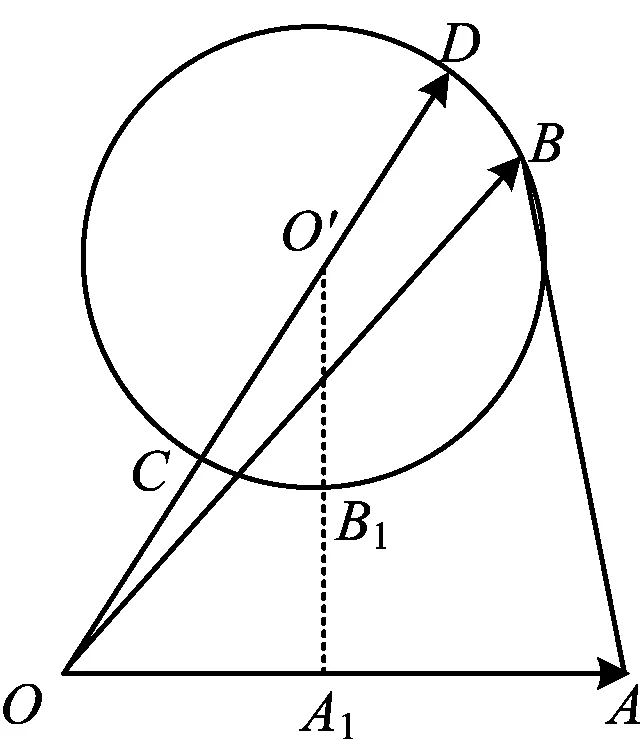
圖1

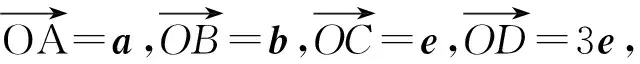
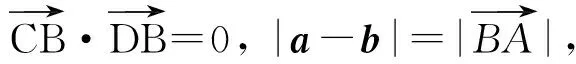
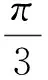
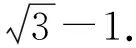
點評本題考查平面向量的數量積、模等基本知識及數形結合思想、轉化思想．解法1比較容易想到，但有一定的運算量，解法2比較簡潔．這兩種解法都把原問題轉化為射線上的點與圓上的點的距離的最小值問題．

1.3 創新設計，聚焦素養

數學核心素養是具有數學基本特征、適應個人終身發展和社會發展需要的必備品格與關鍵能力．數學核心素養包括：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析．

試卷對基礎知識、基本方法考查的同時，突出對數學核心素養的考查．試卷充分體現以知識為載體、方法為依托、能力為導向的命題特點，突顯試題的選拔功能．如：

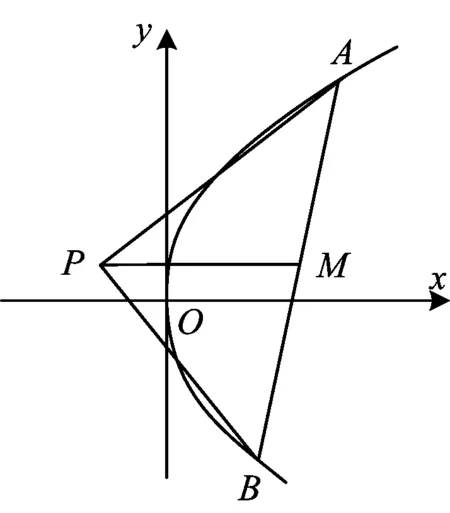
圖2

例3如圖2，已知點P是y軸的左側(不含y軸)一點，拋物線C:y2=4x上存在兩個不同的點A,B滿足PA,PB的中點均在C上．

1)設AB的中點為M,證明:PM⊥y軸；

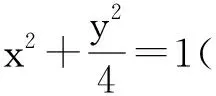
(2018年浙江省數學高考試題第21題)

本題考查拋物線、橢圓的簡單幾何性質及解析幾何的基本思想方法和直觀想象、數學運算、邏輯推理等數學核心素養，避開了平時學生大量操練的“聯立直線與圓錐曲線方程，然后進行消元”的解題模式．

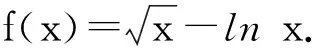
1)若f(x)在x=x1,x=x2(其中x1≠x2)處的導數相等，證明：f(x1)+f(x2)>8-8ln 2；

2)若a≤3-4ln 2，證明：對于任意k>0，直線y=kx+a與曲線y=f(x)有唯一的公共點．

(2018年浙江省數學高考試題第22題)

此題是以人教A版教材《數學(必修1)》第88頁的例1“求函數f(x)=lnx+2x-6的零點個數”為藍本改編而來，命題組給出的第2)小題的解答與課本的此例方法是相同的，從而體現了“題在書外，根在書中”．

第1)小題與以下例5屬于相關題：

例5已知函數f(x)=x2+aln(x+2)存在兩個極值點x1,x2.

1)求實數a的取值范圍；

2)記S=f(x1)+f(x2)，求S的取值范圍．

第2)小題與以下例6屬于相關題：

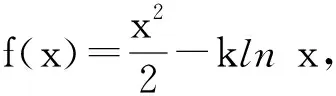
1)求f(x)的單調區間和極值；

(2015年北京市數學高考文科試題第19題)

例4中兩個小題的解答與上述兩個相關題的解答也相似．

試卷改變前3年以數列不等式作為壓軸題，函數與導數重返壓軸題位置，此題設計的函數有唯一的駐點(4,2-2ln 2)與拐點(16,4-4ln 2).命題組通過挖掘幾何性質精心設計問題，體現了導數的基本運用，考查了學生綜合運用知識分析問題、解決問題的能力，及直觀想象、數學抽象、邏輯推理、數學運算等數學核心素養．

命題組給出本題的參考答案為：第1)小題將f(x1)+f(x2)表示為關于x1x2的函數，利用已知條件及基本不等式確定x1x2的取值范圍，從而解決問題；第2)小題先構造符號相反的函數值，再運用函數零點存在定理證明零點的存在性，然后運用函數的單調性證明零點的唯一性．構造符號相反的函數值，學生很難想到，實質是極限思想下的構造．

限于篇幅，本文僅給出例4的另外一種解法．

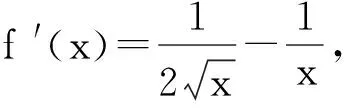
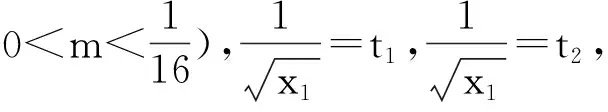
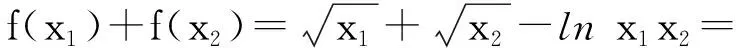
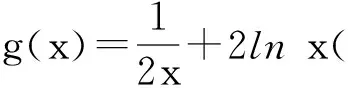
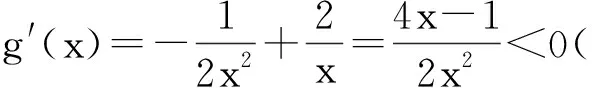
從而g(x)為減函數.因此

即

f(x1)+f(x2)>8-8ln 2．

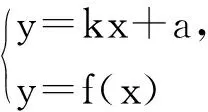
f(x)-kx=a.

記F(x)=f(x)-kx，則

當x→0+時，F(x)→+∞；當x→+∞時，F(x)→-∞．

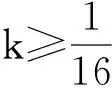
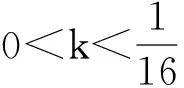
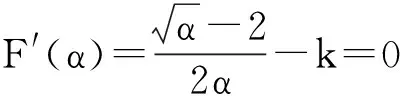
故

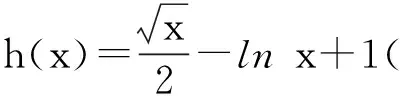
從而h(x)單調遞減，于是

h(x)>h(16)=3-4ln 2,

即

F(α)>3-4ln 2≥a,

亦即

F(α)>a,

故方程F(x)=a必有唯一的實數解，即直線y=kx+a與曲線y=f(x)有唯一的公共點．

點評第1)小題的參考答案選擇t=x1x2為自變量，需運用基本不等式，而筆者所給出的解法選擇m為自變量，回避了基本不等式；第2)小題的參考答案分離參數k，而筆者所給出的證法分離參數a，利用極值解決問題，入手比較容易．

2 試卷的不足

試卷第18題第2)小題考查配角法；第20題第2)小題考查錯位相減法，配角法與錯位相減法都屬于解題技巧，“是否屬于中學數學的基本方法、是否應該作為重點考查”有待商榷.

從閱卷結果看，中檔學生的數學水平拉不開檔次，原因是中檔題目偏少了些，低檔題目偏多了些，低、中、高檔題需要合理配置．

3 對教學的啟示

文理合卷后，命題的風格發生了改變，我們的教學也應作相應的改變．

在新授課教學中，研究《課程標準》，基于《課程標準》，立足教材，重視教材的使用，揭示概念的發生、發展過程，建構數學概念，理解數學本質，突出思維能力和運算能力的培養．

在復習課教學中，把課本上的知識、方法重組與概括，揭示其內在聯系與規律，形成網絡，克服盲目做題、重復操練，訓練學生思維的深刻性和批判性，培養獨立思考能力．這樣才能把基礎知識、基本技能、基本思想方法落到實處．

學習數學，除了獲取必要的數學知識和掌握必要的數學技能之外，更重要的是獲得基本的數學素養.為培養學生的數學核心素養，教師要了解學生核心素養的習得規律．在教學過程中，培養學生對問題一種分析的態度、一種探究的目光，對課堂上的某些問題適當加以延伸、推廣等，并引導學生加以解決，使學生的數學關鍵能力和學習力獲得提升，實現有意義的深度學習．