基于事件驅動的容積卡爾曼濾波定位算法

，，，*

1.火箭軍工程大學，西安 710025 2.火箭軍駐7103廠軍事代表室，西安 710100

網絡化控制系統(Networked Control System, NCS)憑借其分布式和模塊化的特點在傳感器網絡、微機電系統以及多智能體控制等領域得到廣泛的應用[1]。網絡化狀態估計系統(Networked State Estimation System, NSES)作為NCS的重點技術組成之一，憑借其傳感器和估計器通過無線網絡連接的優勢，極大地增加了傳感器的監測范圍，因此該技術被廣泛應用于目標跟蹤定位、工業設備的狀態監控以及搜救危險區域等領域[2]。

NSES中負責感知探測的傳感器和負責濾波計算的估計器往往分布在不同的空間領域，因此存在以下問題：

1)傳輸網絡的不穩定性和傳輸環境的復雜性往往會導致量測信息的丟失和延遲。

2)傳感器每次向估計器傳輸量測信息都要消耗一定的能量，然而傳感器往往攜帶的能量有限。

3)在傳感器較多的網絡化濾波系統中，信道資源有限，限制了傳感器向估計器傳輸量測信息。

國內外眾多學者對NSES中的通信問題進行了研究，文獻[3-8]對系統中的數據丟包問題展開了深入研究，文獻[9]進一步在數據丟包的基礎上進一步研究了信息傳輸延時問題。文獻[6]和文獻[8]均通過獨立同分布的Bernoulli過程描述了NSES中的丟包問題，文獻[8]重點分析了固定丟包概率對系統穩定性的影響，而文獻[6]則在最小均方誤差條件下推導了次優估值器(包括濾波、平滑和預報)。文獻[9]則設計了線性最小方差意義下的最優線性估計器，并給出了穩態估計器存在的充分條件。為研究信息丟失率對濾波性能的影響，文獻[10]給出了濾波器收斂的臨界丟包條件。

上述文獻均采用隨機過程來描述NSES中的數據被動丟包過程，但為了在有限的通信資源條件下達到最佳的估計性能，一種基于事件驅動的思想在NSES中成為了當前研究的熱點[11-12]。文獻[13]證明了相比于傳統的等間隔采樣方式，基于事件驅動的采樣方式能有效降低系統輸出的方差。文獻[14]提出了基于隨機事件驅動的網絡化狀態估計技術，主要研究了線性系統主動舍棄量測信息條件下的卡爾曼濾波方法。文獻[15]研究了在NCS中如何設計基于事件驅動的控制方法，設計了一種基于連續觀測自身狀態變化率的事件驅動模式。文獻[16]則設計了一種基于當前真實狀態和估計狀態差值的自發事件驅動模式。因此，在事件驅動問題的研究中，如何設計“最優”的事件是關鍵問題之一。

上述研究大多是基于線性系統的，而對非線性系統的研究通常基于EKF算法進行簡單的線性化處理，EKF算法的核心是通過泰勒展開的方式進行線性化處理，因此通常存在求雅克比矩陣過程過于復雜和舍棄誤差較高的問題[17]，不適用于高維度的強非線性系統。

容積卡爾曼濾波(CKF)方法是一種新興的非線性濾波器，CKF通過容積積分規則對Bayes框架下的預測和更新公式進行數值近似，文獻[18]將CKF與傳統的擴展卡爾曼濾波(Extended Kalman Filter,EKF)和無跡卡爾曼濾波(Unscented Kalman Filter,UKF)進行了比較，對其穩定性和性能進行了對比分析，證明了CKF算法在高維度強非線性的系統中效果更好。

本文的研究重點分為兩個方面:一是在隨機事件驅動的基礎上建立了檢測事件驅動模式；二是將事件驅動的思想引入CKF算法框架，推導事件驅動條件下CKF算法的更新方式。最后以天基空間目標跟蹤為背景，建立高維度強非線性的跟蹤系統，分析了同等通信率條件下，不同事件驅動方式下的CKF算法的性能，仿真結果表明，基于檢測事件驅動的CKF算法對空間目標的跟蹤性能良好，具有一定的研究意義和實用價值。

1 問題描述及預備知識

1.1 網絡化狀態估計系統結構

考慮如圖1所示的網絡化最優估計系統。該系統中傳感器和估計器是分離的，傳感器的信息能否成功傳輸到估計器取決于決策器輸出的信號，信息到達與否是決定網絡化濾波系統精度高低的關鍵因素之一。

1.2 非線性濾波系統

考慮如下非線性濾波系統：

(1)

式中：f(·)為狀態的非線性函數，描述了系統狀態量xk的變化過程；h(·)為量測非線性函數，由傳感器的觀測方式決定；vk,wk分別為量測噪聲和系統噪聲，且均為獨立的高斯白噪聲，其方差分別為Rk,Qk。

2 事件驅動建模

2.1 事件驅動的數學描述

定義1：事件驅動模型。

假設決策器中存在某種決策機制p，當滿足該條件時γk=1，否則γk=0，即：

通過對變量γk的建模，可以描述不同類型的事件驅動模型。

2.2 隨機事件驅動

定義2：隨機事件驅動模型。

假設決策器輸出的變量γk服從伯努利分布，其概率分布為p{γk=1}=λ，p{γk=0}=1-λ。λ表示驅動率，當λ=1時，量測信息能全部成功傳輸到估計器；而當λ=0時，所有的量測信息均不能到達估計器，通過控制λ的大小可以對傳感器和估計器的通信率f進行控制。

理論上f=λ，其中f=NΔt/ttotal，N表示量測信息到達估計器的總次數，Δt表示傳感器的采樣間隔，ttotal表示系統工作的總時長。

此時，非線性濾波系統(1)中的量測噪聲vk滿足[1，14]：

(2)

式中，σ→∞，即當量測信息未到達估計器時，觀測系統的觀測噪聲方差趨于無窮大。

隨機事件驅動模型有效降低了通信率，但無法同時兼顧濾波精度，因此本文定義了新的驅動模型。當λ=1時，通信率為100%，隨機事件驅動退化為傳統的無驅動模式。

2.3 檢測事件驅動

定義3：檢測事件驅動模型。

變量γk的取值為：

式中：C為先驗閾值，根據實際情況對精度需求的不同，C的取值不同。此時，非線性濾波系統(1)中的量測噪聲vk仍然滿足式(2)。

檢測事件驅動通過計算量測數據的殘差，當殘差小于閾值C時，表示估計器的跟蹤精度在可接受范圍內，可暫時不接收新的量測數據；而當殘差大于閾值C時，則表示估計器的跟蹤精度已經不能滿足精度要求，需要引入新的量測值對估計器進行修正。當C=0時，檢測事件驅動退化為傳統的無驅動模式。

通過檢測事件驅動，可在滿足精度要求的前提下，最大限度的降低通信率，通過調整閾值C便能達到調整精度標準和間接控制通信率的目的。

3 事件驅動條件下的CKF算法

3.1 事件驅動條件下的線性濾波器

針對如下線性系統：

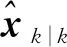
(3)

結論1：將定義1中的事件驅動模型引入線性濾波器后，當γk=1時，估計器保持原有更新過程進行預測和外推；而當γk=0時，估計器進入等待狀態，其量測更新過程如式(4)所示，直至新的驅動指令到達。

(4)

3.2 事件驅動條件下的CKF算法推導

文獻[19]給出了標準CKF算法的詳細推導過程以及算法流程。由于引入事件驅動條件后，僅改變了其量測更新的過程，為簡化表述，下面僅給出了標準CKF算法的量測更新過程：

(5)

(6)

其中預測誤差協方差矩陣Pzz,k|k-1以及互協方差矩陣Pxz,k|k-1的具體求解過程如下：

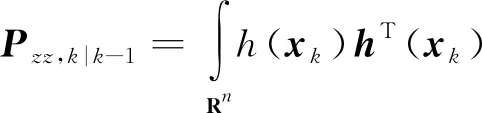
(7)

(8)

其中N(x;μ,P)表示變量x服從均值為μ協方差陣為P的正態分布，式(7)和式(8)的計算可根據容積積分規則[20]進行計算。

假設1：以CKF算法為基礎，引入定義1中的事件驅動模型，估計器的量測更新過程與結論1相同。

證明：當量測值zk是否進入估計器受決策模型(4)控制時，協方差矩陣

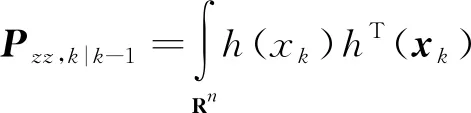
(1-γk)σ2I

(9)

(10)

狀態協方差矩陣Pk|k的更新過程則可以表示為：

(11)

按照式(9)計算Pzz,k|k-1并帶入式(10)和式(11)后可得到：

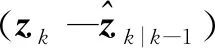
(12)

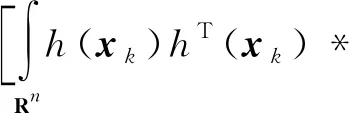
γkRk+(1-γk)σ2I]*Pxz,k|k-1

(13)

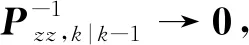
證畢。

結論2：將定義1中的事件驅動模型引入CKF算法后，當γk=1時，估計器根據標準CKF算法更新過程進行預測和外推；而當γk=0時，估計器進入等待狀態，其量測更新過程如公式(4)所示，直至新的驅動指令到達。

3.3 事件驅動條件下的CKF算法框架設計

根據結論2，設計如圖2所示的算法框架。

當圖2中決策事件驅動模塊根據定義2中的隨機事件驅動模型進行工作時，此時算法為隨機事件驅動CKF(Stochastic Event-triggered Cubature Kalman Filter, SECKF)算法；當圖2中決策事件驅動模塊根據定義3中的檢測事件驅動模型進行工作時，此時算法轉變為檢測事件驅動CKF(Detected Event-triggered Cubature Kalman Filter, DECKF)算法。

4 空間目標無源定位系統

4.1 狀態模型

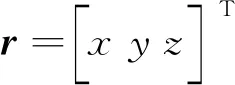
根據二體運動規律[1，21]，目標的運動方程為：

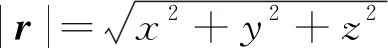
4.2 觀測模型

假設高軌的觀測衛星可通過光學手段獲取空間目標的角度信息。目標在觀測衛星軌道坐標系下測得的俯仰角βk和方位角δk定義如下[22]：

式中：φ=[φxφyφz]T為目標衛星在觀測衛星質心軌道坐標系下的坐標。

定義觀測量z(k)=[βkφk]T，則觀測方程可表示為：

z(k)=H[x(k)]+vk

其中H(·)表示量測非線性函數。

5 仿真結果及分析

5.1 場景設定

某高軌觀測衛星攜帶光電載荷，實時獲取低軌非合作空間目標角度信息，通過將量測信息傳遞給計算中心實現對目標的跟蹤，假設非合作空間目標為某偵察衛星。天基觀測平臺和非合作空間目標在任務開始時刻的軌道6要素[21]如表1所示。

表1 平臺與目標的軌道6要素

通過Matlab仿真得到空間目標與天基觀測平臺的星歷數據，并選取連續可見時間為3 000 s的弧段進行仿真(見圖 3)。

5.2 評價指標建立

為了準確描述算法的性能，便于后續算法性能的比較，建立如下比較標準。

1)均方根誤差RMSE：定義一次濾波仿真試驗中k時刻的均方根誤差

(14)

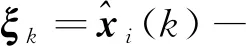
2)位置收斂精度：以仿真最后100 s的位置均方根誤差的平均值作為位置收斂精度。

3)速度收斂精度：以仿真最后100 s的速度均方根誤差的平均值作為速度收斂精度。

5.3 算法參數設置

地面站對空間目標能實現高精度的定軌，但地面站的分布限制了對空間目標的觀測窗口，當空間目標離開地面站的觀測區域后可能存在軌道機動的行為，結合地面站的定軌精度和空間目標的機動能力，本文設定初始位置誤差和初始速度誤差分別為[100 100 100]Tkm、[0.1 0.10.1]Tkm/s。空間目標被動無源定位的角度測量可達到4″～7″的精度，因此假設量測噪聲和系統噪聲是相互獨立的高斯白噪聲，并假設噪聲的方差為先驗信息，其中方位角的方差為σβ=1mrad，俯仰角的方差為σε=1mrad。設定濾波周期T=5 s，而仿真總時長為1 500 s。

5.4 仿真結果分析

在檢測事件驅動條件下，根據上述場景想定以及參數設置，采用DECKF算法對空間目標進行跟蹤，當先驗閾值C取8×10-6時，空間目標理論軌道和估計軌道的對比如圖4所示。

可以看出DECKF算法對目標位置的估計誤差逐步縮小，跟蹤性能穩定。當C分別取8×10-6，5×10-7，3×10-7，0時(其中當C=0可視為傳統無驅動模式下的CKF算法)，進行100次蒙特卡洛仿真，計算得到不同閾值條件下的通信率f分別為0.639，0.793 6，0.873 7和1，圖5為不同閾值條件下的位置和速度的均方根誤差。

從圖5中可以看出，DECKF算法通過檢測事件驅動的形式，在有效降低通信率的同時，濾波精度損失較小，當先驗閾值C取8×10-6時，DECKF算法較之傳統的CKF算法雖然在跟蹤精度上有所下降，但其收斂過程更為平穩，不同閾值條件下DECKF算法的具體跟蹤性能如表2所示。

通過性能分析可以看出，通過調整閾值C，DECKF算法在有效降低通信率的同時能保證濾波精度維持在較高水平。當通信率損失達到20%時，算法的跟蹤精度的損失在10%以內，誤差的數量級未發生改變。

在同等通信率的條件下，即驅動率λ分別取0.173 9、0.793 6和0.873 7時，根據上述的場景想定以及參數設置，采用SECKF算法，進行100次蒙特卡洛仿真，并與DECKF算法進行橫向對比。

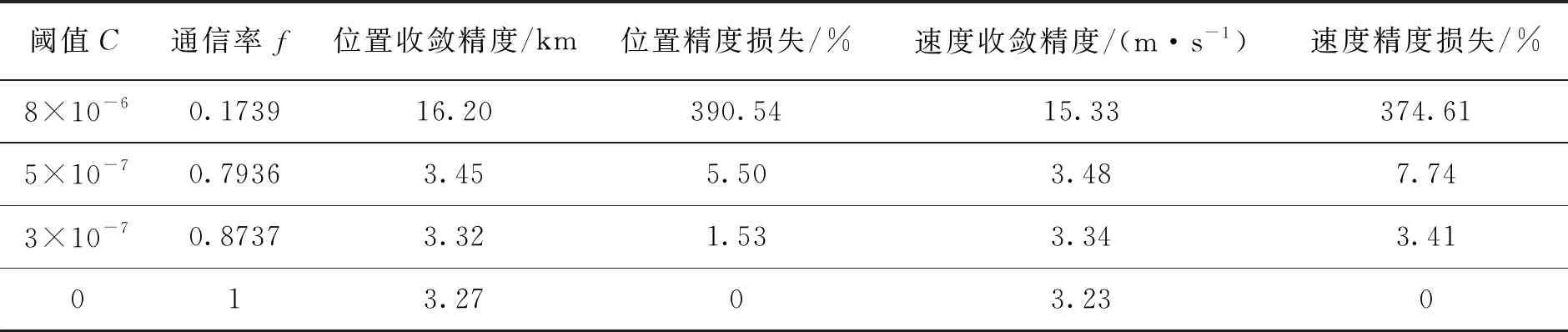
表2 不同閾值條件下DECKF算法性能比較

圖6僅給出了λ=0.173 9時兩種算法的性能比較結果，可以看出，在同等通信率條件下，檢測事件驅動的濾波精度明顯高于隨機事件驅動。不同通信率條件下，DECKF算法的具體性能優勢如表3、表4所示。

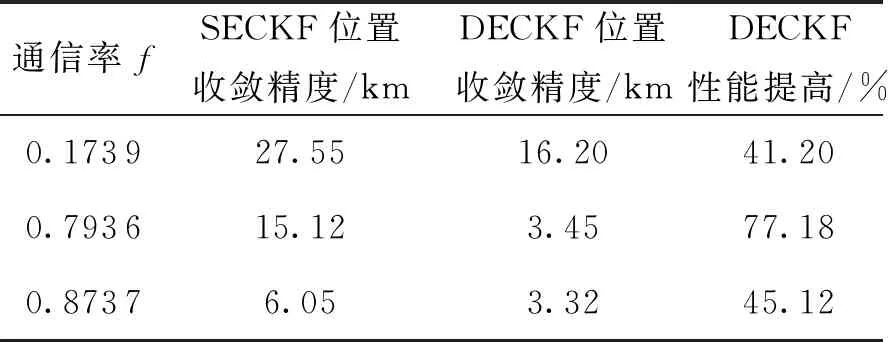
通信率fSECKF位置收斂精度/kmDECKF位置收斂精度/kmDECKF性能提高/%0.173927.5516.2041.200.793615.123.4577.180.87376.053.3245.12

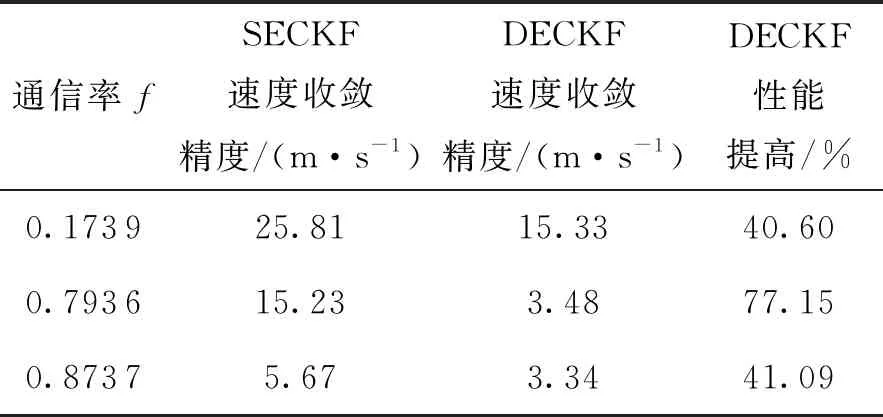
表4 DECKF與SECKF的算法速度收斂精度比較

6 結束語

以基于事件驅動的網絡化非線性濾波系統為研究對象，本文的主要工作和研究結論如下：

1)為了在網絡化濾波系統低通信率的條件下達到較高的跟蹤精度，在隨機事件驅動的基礎上建立了一種基于殘差檢測的事件驅動模式。

2)針對非線性系統，將兩種事件驅動模式引入CFK，設計了事件驅動條件下的CKF算法框架，并推導了事件驅動條件下的CKF更新過程，得到了DECKF和SECKF兩種算法。

3)以天基僅測角的空間目標跟蹤問題為背景，分析了不同檢測閾值對DECKF算法性能的影響，通過與標準CKF的比較發現，DECKF在減少20.64%的通信率的情形下，位置跟蹤精度和速度跟蹤精度僅下降了5.50%和7.74%。

4)橫向比較了DECKF算法與SECKF算法的性能，在同等通信率條件下，DECKF算法的濾波精度相比SECKF提高40%以上。

5)本文通過調整閾值達到了調整通信率的目的，但不能直接根據通信率的臨界值設置直接指導算法的參數設置，因此如何根據通信率約束自適應的調整參數還有待于進一步的研究。