與XY雙自旋鏈耦合的雙量子比特系統的關聯性與相干性?

楊陽 王安民 曹連振 趙加強 逯懷新

1)(濰坊學院物理與光電工程學院,山東省多光子糾纏與操縱實驗室,濰坊 261061)2)(中國科學技術大學近代物理系,合肥 230026)(2018年4月25日收到;2018年5月20日收到修改稿)

1 引 言

量子相干性源于量子力學的疊加原理,在量子信息處理中扮演著重要的角色.比如在糾纏產生[1,2]、量子計量學[3?5]、量子熱力學[6?8]以及量子生物學[9?11]中都有著廣泛的應用.

Baumgratz等[12]提出了一個量化量子相干性應滿足的條件.多個量子相干度量方法隨之被提出,比如相對熵相干度量和l1范數相干度量,二者都是基于所考察量子態與非相干態集合間的某種最小距離而定義的.基于凸頂方法的生成度量[13,14]、基于操作[15,16]以及基于量子糾纏[2]的相干度量也相繼被提出.在準確度量相干態相干性的基礎上,人們對量子相干性的多個方面展開研究,比如量子相干性與量子糾纏的轉化[17,18].量子關聯在量子算法[19,20]、遠程量子態制備[21]等量子信息任務處理中同樣扮演著重要的作用,因此量子相干性與量子關聯的關系也引起了人們的關注[22?24].

現實中,量子系統不可避免地要與環境發生相互作用而丟失相干性,進而不能有效地執行量子信息處理任務.量子關聯在實際處理任務中,也遭到環境噪聲的破壞,但是無論是Markovian還是非Markovian環境,人們對量子關聯的破壞研究相對較多[25?28].量子關聯可以不受某些具體噪聲的影響而保持不變,同時量子關聯與經典關聯之間存在突變效應[29?34].Bromley等[35]首先發現對于某些特定的量子系統,當體系處于某些特殊的初態時,基于距離的量子相干度量保持不變,即會發生相干凍結現象.Yu等[36]給出了量子系統的相干性完全凍結的條件.相干性一旦遭到破壞,量子系統處理量子信息任務的能力也隨即被破壞.所以環境作用下量子系統相干性演化規律吸引了眾多學者進行研究[37?44].本文主要研究自旋鏈環境作用下,系統相干性與關聯性的演化規律.

本文將具有Dzyaloshinsky-Moriya(DM)相互作用的XY自旋鏈作為量子系統所處的環境,考慮雙量子比特系統的量子態的演化規律,推導出某些初態的相干性演化公式,并與系統的關聯相比較.我們發現量子相干性在不同的時間段有不同的對應,在tt0時,則與量子關聯完全相同.同時,我們考慮了DM相互作用對量子相干性的影響.

2 雙XY自旋鏈中雙量子比特的演化

由兩個無相互作用的自旋組成的雙量子比特A,B構成的系統在具有DM相互作用的獨立XY自旋鏈環境下的哈密頓量為

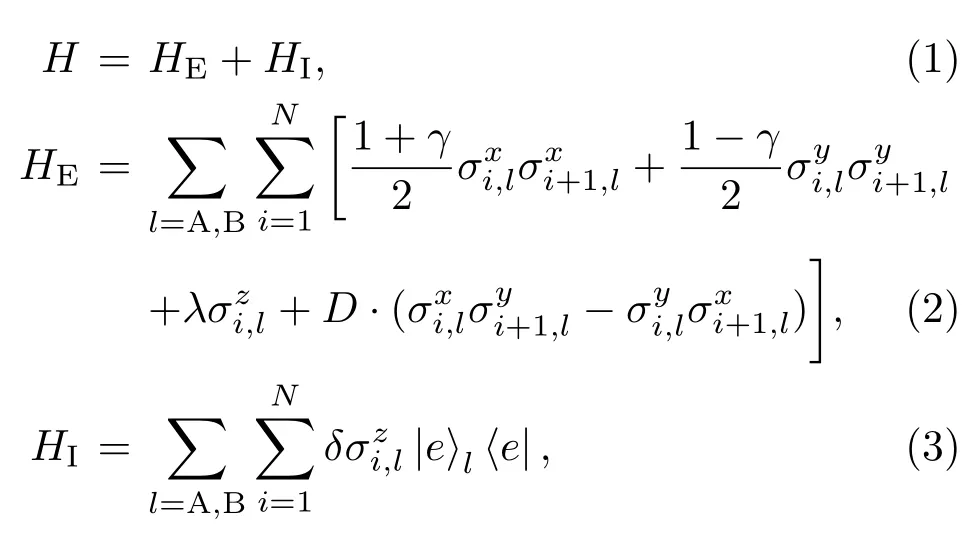
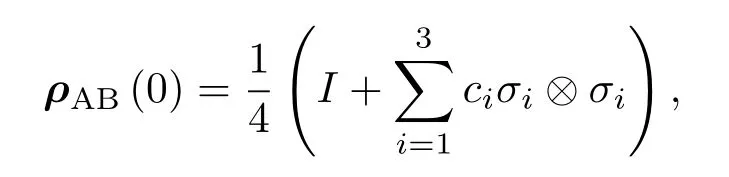
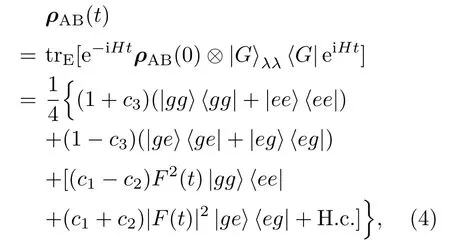
σi(i=x,y,z)為泡利算符.系統的密度算符演化為其中,λg= λ.利用Jordan-Wigner與Bogoliubov變換,可以被對角化為[45?47]

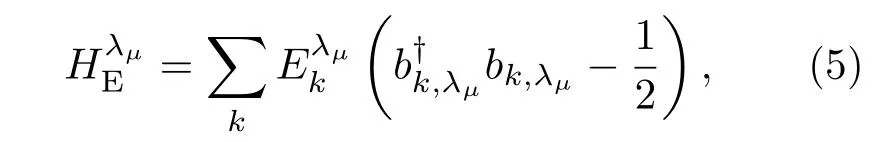
其中

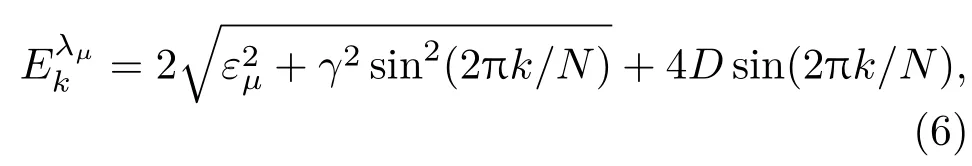
εμ= λμ? cos(2πk/N),k= ?M,···,M, 且M=(N ?1)/2.HλμE對應的基態

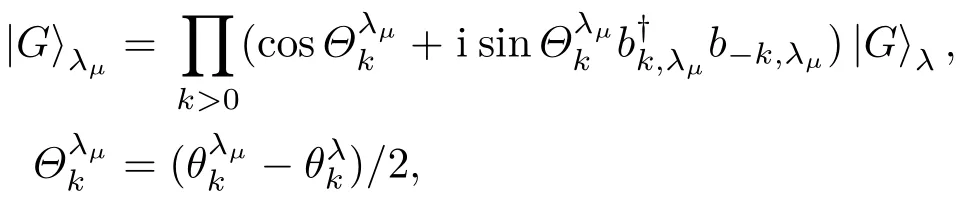
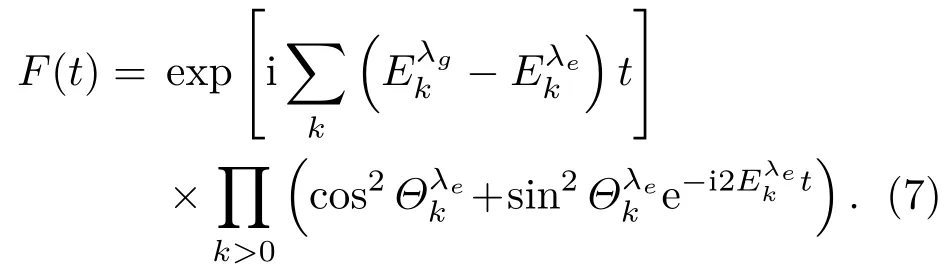
與XY自旋鏈相比較,具有DM相互作用的XY自旋鏈有明顯的區別,一是能譜中含有相互作用強度D,二是中含有Bogoliubov變換角度因此DM相互作用可能對量子相干性產生影響,其影響將由|F(t)|的具體表達式

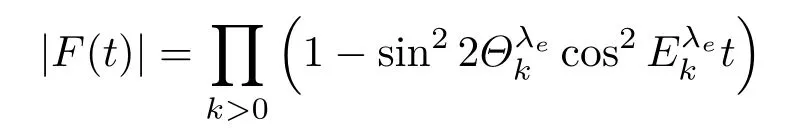
來決定.

3 量子失協與量子相干度量

量子失協被用來量化量子關聯,是由經典互信息過渡到量子情形下所產生的差異而來[48].對雙量子系統,其定義為

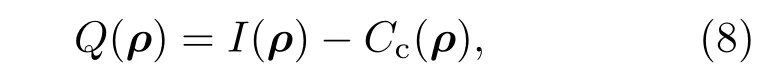
其中I(ρ),Cc(ρ)分別為總關聯、經典關聯;

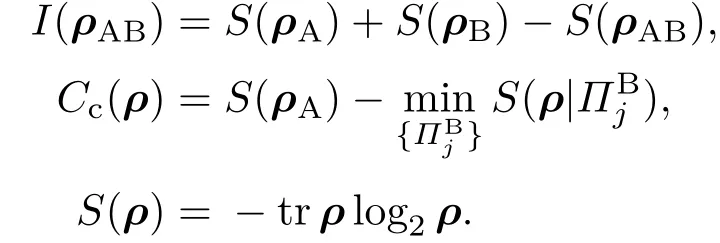
Baumgratz等[12]給出了嚴格量化量子相干性所應滿足的條件:(i)非負性,C(ρ)>0,只有非相干態才等于零;(ii)單調性,C(ρ)>C(Λ(ρ)),Λ為非相干操作;(iii)強單調性,其中λ為非相干操作,(iv)凸性,C(qρ+(1?q)τ)6 qC(ρ)+(1?q)C(τ).基于此,相對熵相干度量被提出,其定義為

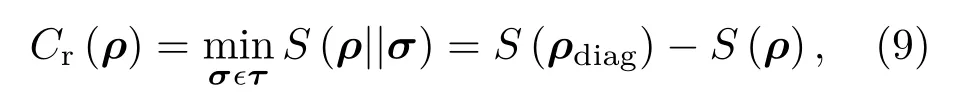
其中τ為非相干態集合,ρdiag為ρ的對角元組成的矩陣.

4 量子相干動力學

不失一般性,選取c1=1,c2=?c3,由(8)式得雙量子比特系統的總關聯為

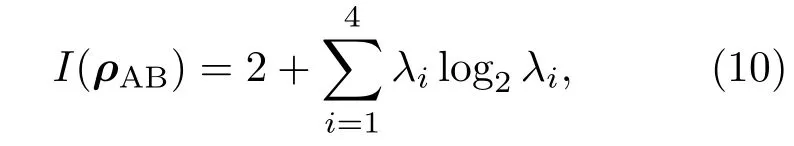
其中

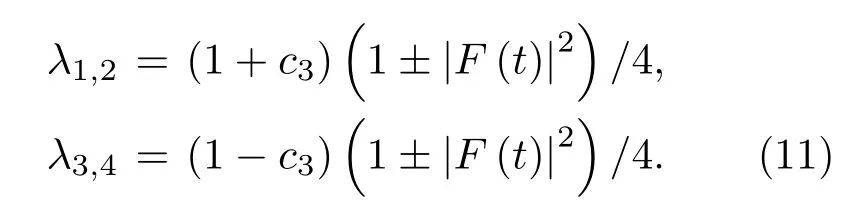
系統的量子關聯為

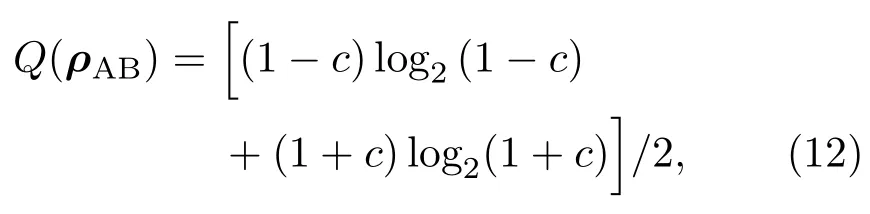
由(9)式得系統的相對熵相干度量為

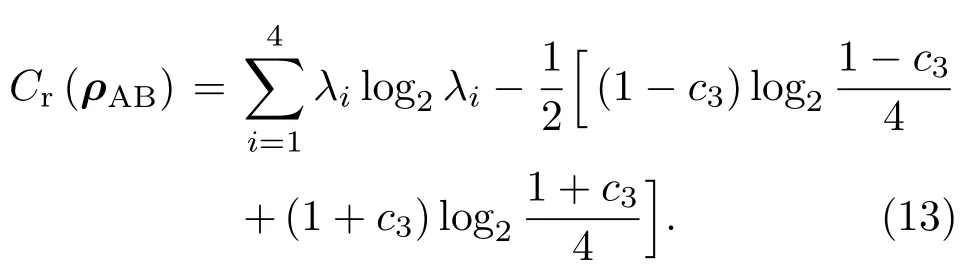
利用量子關聯或者相干性都可以探測到XY自旋鏈在λ=1處存在相變點[33].現在主要考慮相變點λ=λc=1附近的關聯以及相干性的演化情況.選取δ=0.1,γ=0.5,c3=0.8,N=401時,圖1(a)展示了D=0時關聯與相對熵相干度量的演化.發現在t=t0處量子關聯與經典關聯存在突變,突變時刻t0滿足|F(t0)|2=c3.當tt0時,經典關聯不隨時間而改變,量子關聯發生演化.有趣的是,當tt0時,則與量子關聯完全相同.說明tt0時,(12)式中的c由c3變為|F(t)|2,此時可將(13)式整理為(12)式,因此量子關聯與相干性的演化完全相同.現在我們從物理上進行分析,量子相干性的測量依賴于具體基矢的選擇,(9)式的相對熵測量中子系統B所選擇的測量基為{|g?,|e?};而量子關聯的測量則必須選擇最優基來進行測量.當t>t0時,測量量子關聯所選擇的最優基為{|g?,|e?},與量子相干性的測量基相同,所以量子關聯與量子相干性完全相同,這與文獻[37,38]中所論述的最優基理論相一致.同時,雙量子比特系統獨自與廣義自旋鏈環境相耦合,與系統中量子比特分別與玻色環境和Ising自旋鏈環境相耦合的情形相比,關聯與相干性的等價關系相似[49].DM相互作用的影響可以從圖1(b)和圖1(c)展現出來,DM相互作用并不改變相干性與關聯性的特點,而是加快相干性與關聯的衰變,轉變時刻隨著D的增加而提前.

圖2展現了不同各向異性參數γ對量子相干性與關聯的影響,其中δ=0.1,D=0,c3=0.8,N=401.隨著各向異性參數γ的增加,退相干效應加快,這與中心雙量子比特系統與一條XY自旋鏈的耦合情形相似[45,46].而當選取γ=0.5,D=0,c3=0.8,N=401時,圖3展示了不同耦合強度δ下的量子關聯與退相干的演化.我們發現耦合強度δ同樣能使相干性與量子關聯的衰變加快.

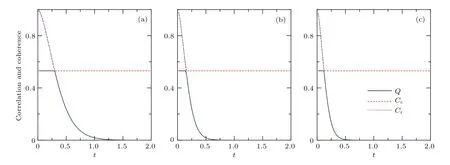
圖1 不同DM相互作用下關聯性與相干性的演化規律 (a)D=0;(b)D=0.4;(c)D=0.6Fig.1.The evolution of correlations and coherence for dif f erent values of the DM interaction:(a)D=0;(b)D=0.4;(c)D=0.6.

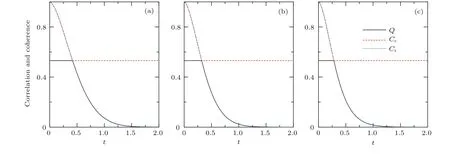
圖2 不同各向異性參數下關聯性與相干性的演化規律 (a)γ=0.2;(b)γ=0.4;(c)γ=0.6Fig.2.The evolution of correlations and coherence for dif f erent values of the anisotropy parameter:(a)γ=0.2;(b)γ=0.4;(c)γ=0.6.

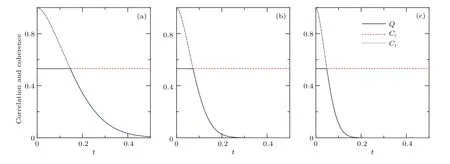
圖3 不同耦合常數下關聯性與相干性的演化規律 (a)δ=0.2;(b)δ=0.4;(c)δ=0.6Fig.3.The evolution of correlations and coherence for the dif f erent coupling constants:(a)δ=0.2;(b)δ=0.4;(c)δ=0.6.

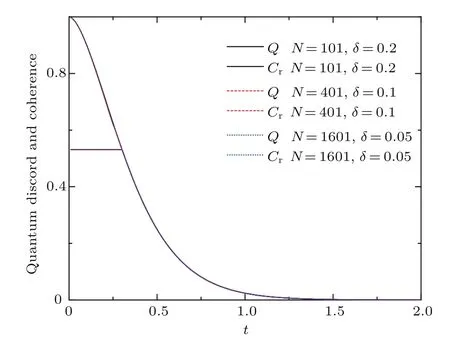
圖4 γ=0.5,D=0,c3=0.8時不同自旋鏈粒子數與耦合常數下量子關聯與量子相干的演化規律Fig.4.The evolution of quantum correlation and quantum coherence for dif f erent values of size of the chain and coupling constants at γ=0.5,D=0,c3=0.8.

5 結 論

本文研究了雙量子比特系統分別獨自與具有DM相互作用的XY自旋耦合下的量子相干性與關聯動力學.量子相干性與量子關聯分別采用相對熵、量子失協來度量.推導出了相干性與關聯性的演化規律.發現在自旋鏈的臨界點附近,系統相干性的演化與關聯的演化存在統一性.在量子關聯未衰變階段,相干性的演化與經典關聯的演化完全相同,而后則與量子關聯的演化完全相同.此外,還發現各向異性參數γ、DM相互作用強度D以及耦合強度δ并不改變量子相干性以及關聯的演化特點,但隨著參數增加會使相干性及關聯性的衰變加快.