調諧質量阻尼器對漂浮式風力機穩定性的影響

黃致謙， 郝文星， 李 春，2， 葉 舟

(1.上海理工大學 能源與動力工程學院，上海 200093； 2.上海市動力工程多相流動與傳熱重點實驗室，上海 200093)

隨著陸上風電場可開發資源的減少，海上風能因能量密度高、湍流度低等優勢逐漸被世界各國重視，“由陸地向海洋”也已成為未來風電場發展的必然趨勢[1-2]。目前，海上風電場主要集中在淺水區域，對于風資源更豐富、風況更優的深水區域，使用漂浮式風力機更加經濟。與陸上風力機不同，海上風力機在運行過程中始終承受波浪載荷作用，因此其載荷特性更加復雜。與固定式風力機相比，漂浮式風力機底部基礎不固定，其始終處于不平衡受力、非定常運動狀態，此非線性載荷不僅會影響機艙內傳動系統的正常工作，也會降低風力機的發電效率，甚至可能發生塔架屈曲、傾覆等事故[3-5]。與傳統海工平臺相比，漂浮式風力機平臺重心位置更高、水線面更小，波浪載荷加劇了平臺的運動，劇烈的運動甚至會導致平臺傾覆。因此，探究如何保障漂浮式風力機在復雜多變的海洋環境中安全穩定地運行具有重要意義。

目前，國內外學者針對漂浮式風力機的穩定性展開了諸多研究。文獻[6]中提出將螺旋側板應用于漂浮式風力機Spar平臺的結構設計中，并采用勢-黏結合的方法研究螺旋側板對Spar平臺動態響應的影響。針對漂浮式風力機對風載荷和波浪載荷響應過大的問題，文獻[7]中提出共用系泊的大型漂浮式風電場概念，并基于水動力軟件Aqwa研究其運動響應特性，發現共用系泊可明顯提高平臺穩定性。以上研究的不足之處在于將葉片、塔架和平臺等結構簡化為剛體，風載荷簡化為軸向推力，這種簡化無法精確描述非定常氣動載荷，更無法揭示在風、波浪載荷下塔架、葉片等結構的變形、屈曲等非線性動態響應過程。部分學者通過控制葉片變槳和電機變扭矩來降低葉片氣動載荷，進而提高漂浮式風力機的穩定性。Namik等[8]研究了獨立變槳對平臺運動的控制效果。Fischer等[9]提出一種基于加速度反饋的非線性控制方法，在理論上分析漂浮式風力機的穩定性。以上研究雖然在一定程度上提高了漂浮式風力機的穩定性，但會加劇葉片根部的疲勞載荷。

調諧減振裝置作為結構控制技術被廣泛應用于高聳柔性結構設計中，實驗和數值計算表明其對于高樓、電視塔等高聳柔性結構具有明顯的減振效果[10]。調諧減振阻尼器主要包括調諧質量阻尼器(TMD)和調諧液體阻尼器(TLD)。文獻[11]中將TMD應用于海上風力機塔架中，并采用有限元方法研究其對風力機塔架振動的減振效果。Stewart等[12]、Lackner等[13]和Sethuraman等[14]研究了TMD對漂浮式風力機穩定性的影響，但未考慮外載荷作用，僅為自由振動分析。關于提高漂浮式風力機穩定性的研究雖在TMD結構控制方面取得了諸多成果，但均做了適當簡化。

因此，筆者采用在機艙配置TMD的控制方法，研究其對海上漂浮式風力機塔頂位移和平臺搖蕩特性穩定性的控制效果，以期為海上漂浮式風力機的穩定性控制提供一定的理論參考。

1 研究對象

研究對象為基于ITI Barge平臺的NREL 5 MW風力機，其參數如表1所示[15]，平臺參數如表2所示[16]。漂浮式風力機模型如圖1所示。

表1 NREL 5 MW風力機參數

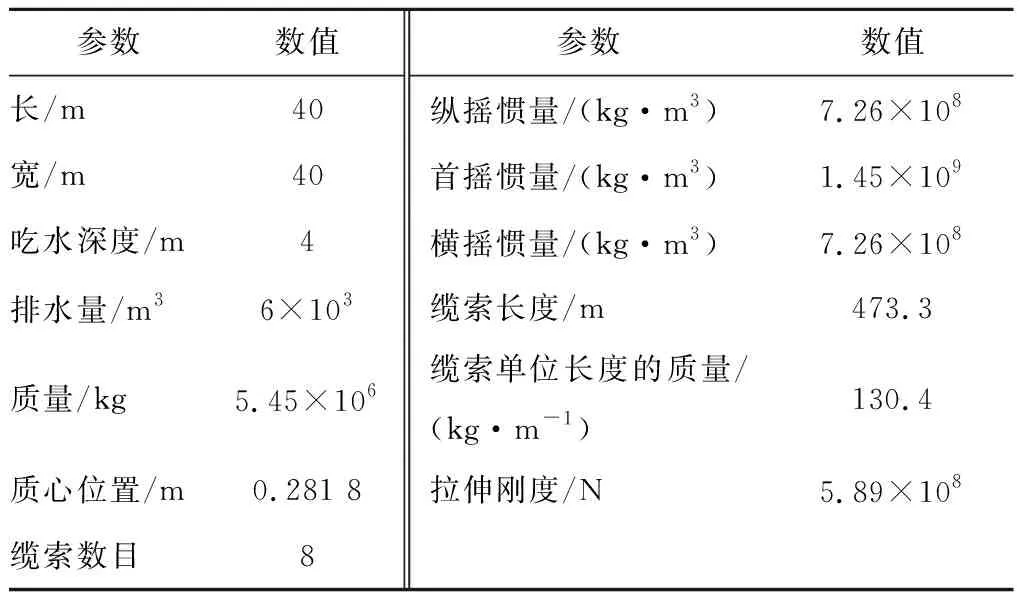
表2 ITI Barge平臺參數

圖1 漂浮式風力機和Barge平臺示意圖

Fig.1 Schematic diagram of the floating wind turbine and Barge platform

2 研究方法

利用基于NREL開發的氣動彈性結構動力學仿真軟件FAST研究TMD對漂浮式風力機結構動力學響應的影響。FAST軟件中考慮氣動-水動-結構-控制耦合并基于時間推進方法實現對非線性運動方程的求解[17-18]。在氣動模塊中，考慮軸向及切向風誘導影響的情況下基于Pitt-Peters動態入流理論求解風輪平臺誘導速度;基于葉素-動量理論，在考慮葉尖損失及輪轂損失的情況下求解風輪氣動力，并采用Beddoes-Leishman動態失速模型進行修正。利用水動模塊計算漂浮式風力機平臺的水動力載荷，包括水線面的面積慣性矩和浮力；漂浮式風力機平臺屬于大尺度結構物，可采用輻射/繞射理論求解波浪力；系泊系統采用懸鏈線模型。在彈性模塊中，結合Kane方法和模態法，在考慮子結構剛柔特性的條件下建立風力機多體動力學模型，其中葉片、塔架和低速傳動軸為具有分布質量、剛度和模態等屬性的柔性體模型，將輪轂、高速傳動軸和機艙等視為剛性體模型。以氣動模塊求解所得氣動力和水動模塊求解所得水動力作為輸入載荷，得到該時間步長下的結構動力學響應，并反饋至控制模塊、水動模塊和氣動模塊，控制模塊會根據結構模塊的反饋信息進行相應的控制，如變槳控制、偏航控制和TMD控制等。仿真流程如圖2所示。

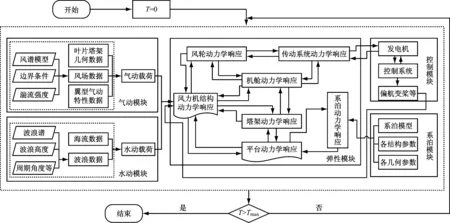
圖2 仿真流程

3 TMD及其動力控制方程

TMD由質量系統、彈簧系統、阻尼系統和支撐系統組成，TMD通過改變自身質量或剛度來達到調整自振頻率的目的，使其接近被減振結構的固有頻率或外部載荷頻率。當被減振結構在外部載荷下產生振動時，會帶動TMD振動，TMD產生的調諧慣性力反作用于被減振結構，并通過阻尼系統將能量耗散，以達到結構穩定性控制的目的。將TMD布置在機艙內部，如圖3所示。

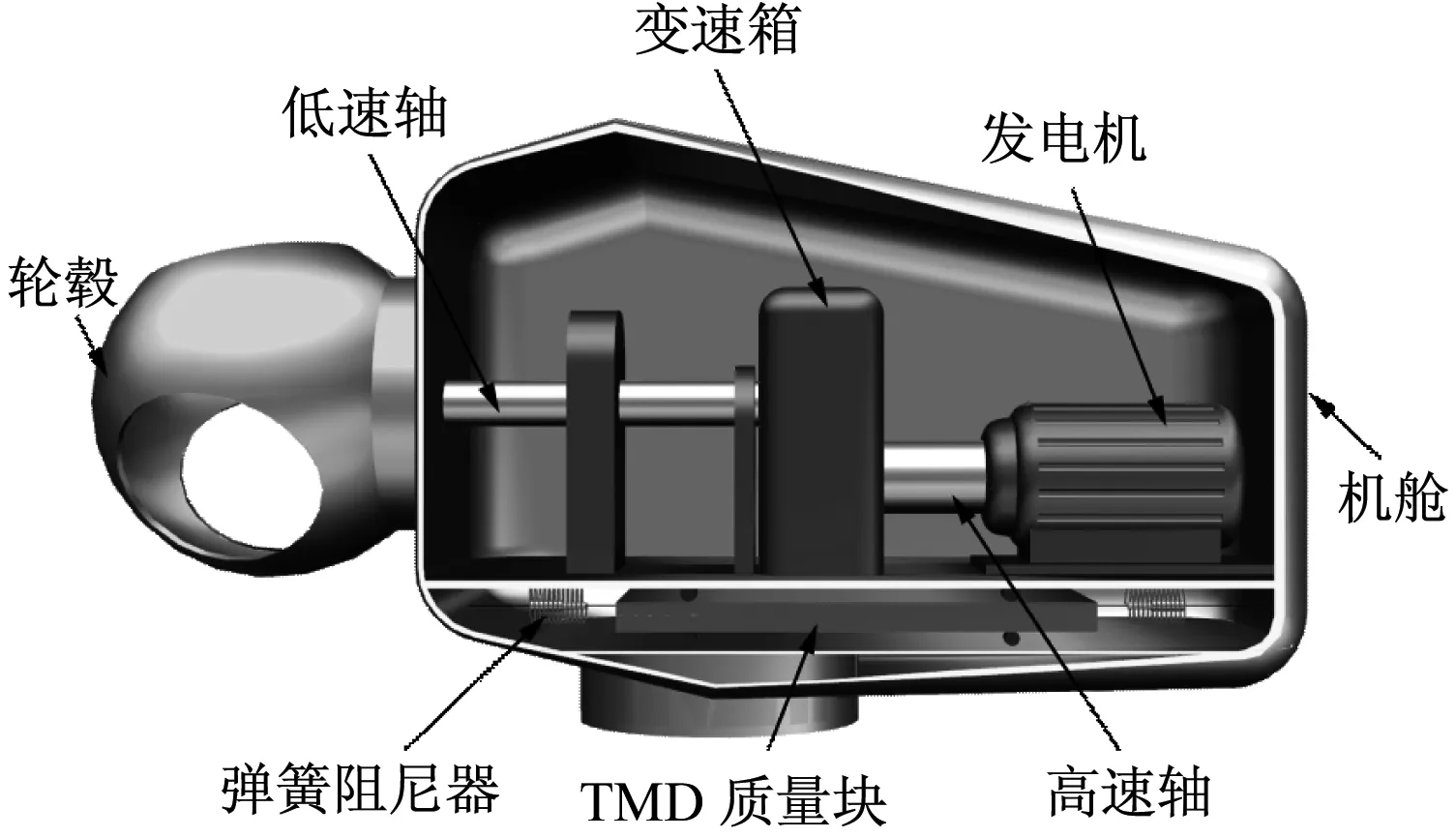
圖3 機艙布置TMD示意圖

4 湍流風場及不規則波浪建模

4.1 風場模型建立

為模擬時歷高風速湍流風作用下漂浮式風力機的結構動力學響應特性，需建立隨時間和空間變化的湍流風模型。常見的風場建模方法分別為基于測風塔的實測數據，即通過模糊邏輯預測、神經網絡預測等方法得到一定空間范圍內的風速分布，適用于小空間風場建模；基于大渦模擬方法(LES)，即在考慮大氣邊界層效應等條件下實現風場建模，所需計算資源極大；基于風電場實測數據，即通過氣象分析方法獲得風場風速數據，適用于小尺度空間風場建模。鑒于此，筆者基于Kaimal風譜并考慮空間相干性建立了三維時歷風場模型。

根據風力機的幾何參數，設定風場覆蓋區域尺寸(水平和垂直方向)為195 m×195 m。由于漂浮式平臺有6個自由度，導致葉片存在垂蕩和橫蕩運動，為保障三維風場始終完全覆蓋葉片，故風場布置較大，風場區域遠超過風輪的掃略區域。設定網格節點為15×15，如圖4所示。考慮空間相干性，通過Kaimal風譜獲得每一節點的風速分布，通過空間相干模型獲得整個風場的風速分布。空間相干模型如下:

(1)

式中：Si,j(f)為節點i、j的互功率譜；C(Δr,f)為空間相干大小；Δr為節點間距離；Si,i(f)和Sj,j(f)分別為節點i、j的功率譜。

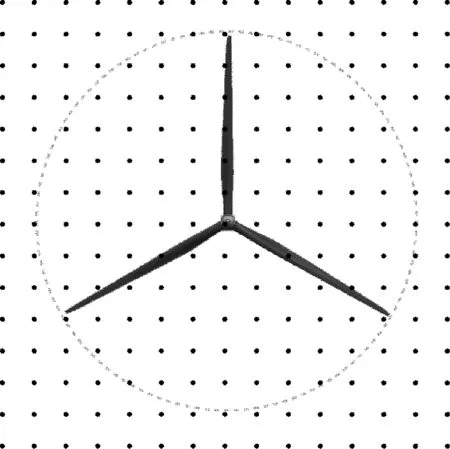
圖4 風場計算區域及網格

以輪轂中心為參考點，以時歷平均風速11.4 m/s為參考風速，仿真時間為600 s，建立三維時歷湍流風風場，輪轂高度處三維風速分布如圖5所示。輪轂點時歷風速分布如圖6所示。由圖6可知，湍流風在u方向的風速波動范圍為10.52～12.55 m/s，v方向的風速波動范圍為-1.052 0～0.993 2 m/s，w方向的風速波動范圍為-0.637 8～0.664 8 m/s。

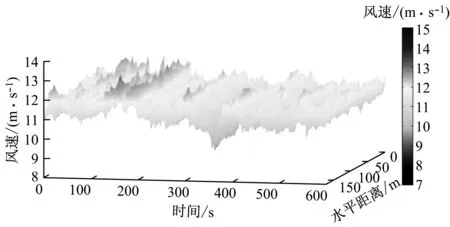
圖5 輪轂高度處的風速分布

4.2 波浪譜及不規則波浪建模

波浪譜以風和波浪為參量，通過定義有義波高、波浪周期和有限風區等參數，即可得到波浪的大致形式。波浪譜是隨機波浪的重要統計信息，可直接給出波能相對頻率和方向的分布。國內外學者研究海洋結構時對波浪載荷幾乎均采用波浪譜方法[19-23]。目前，常見的波浪譜有P-M譜、Jonswap

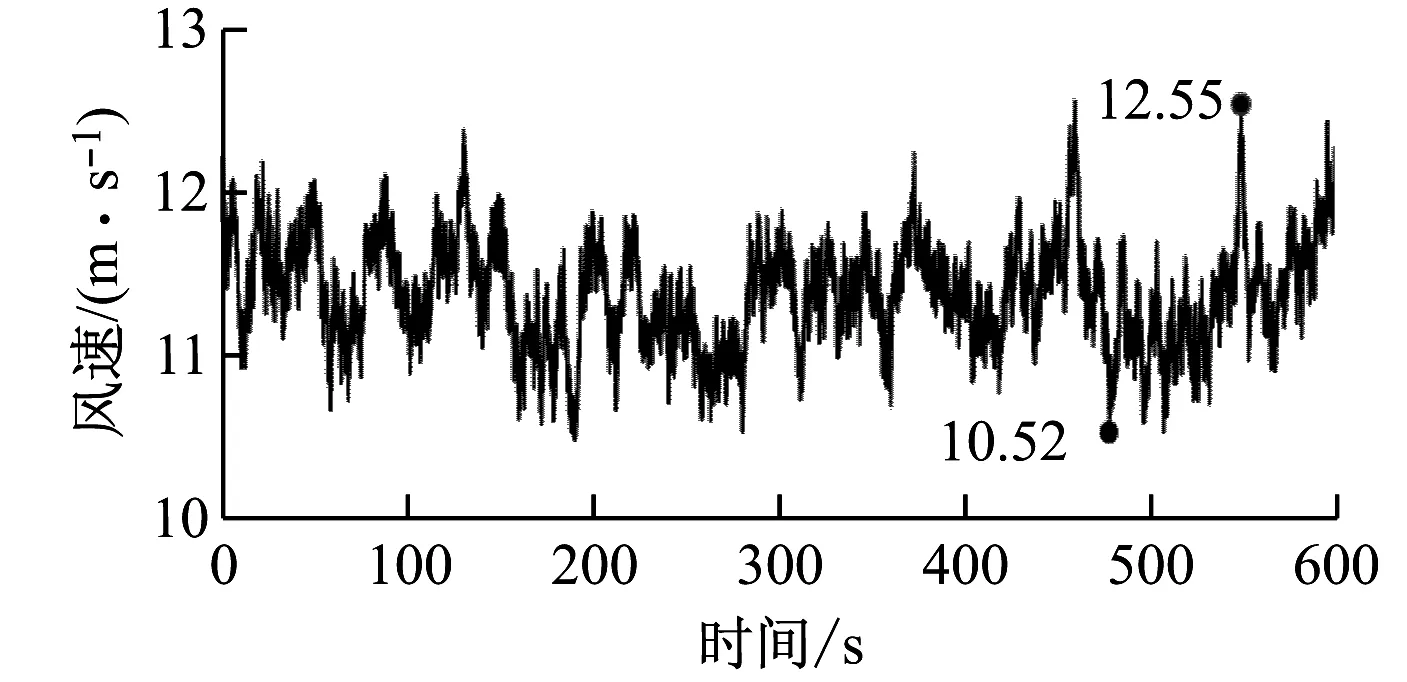
(a) u方向風速分布

(b) v方向風速分布

(c) w方向風速分布

譜和布氏譜等[24]。其中，可由大西洋波浪統計數據分析得出P-M譜，其適合描述充分發展的波浪[25]，可表示為

(2)

式中：Sζ(ω)為功率譜；U為某參考高度處的平均風速；g為重力加速度；ω為波浪圓頻率。

選取P-M波浪譜生成的有義波高為5 m，波浪譜峰周期為12.4 s，基于設定參數建立不規則波浪場，如圖7所示。

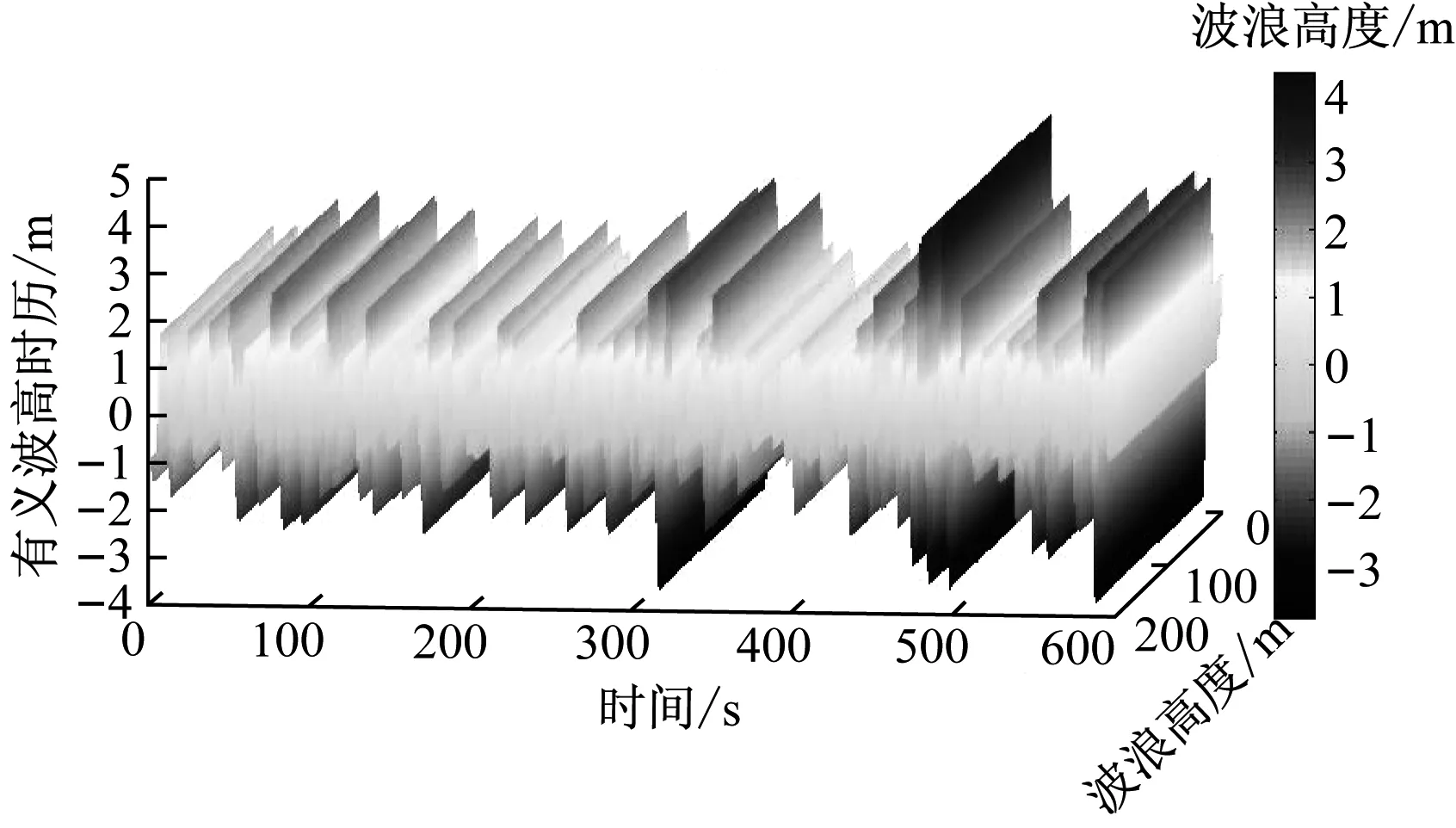
圖7 不規則波浪模型

5 TMD對漂浮式風力機穩定性的影響

在風載荷和波浪載荷作用下,漂浮式風力機的穩定性主要表現為塔頂位移特性和平臺的搖蕩特性。塔頂位移過大會引起風輪葉片在旋轉過程中不穩定，誘發塔架大幅振動并導致失穩，而平臺搖蕩特性與漂浮式風力機整機結構的強度及疲勞載荷有關，對風力機的安全性有很大影響。故筆者主要研究在風、波浪載荷作用下TMD對漂浮式風力機塔架塔頂位移和平臺搖蕩特性的影響。

5.1 TMD對平臺搖蕩特性的影響

漂浮式風力機在TMD控制下平臺搖蕩特性的時歷曲線如圖8所示，橫坐標為時間，縱坐標為平臺各自由度的運動響應。

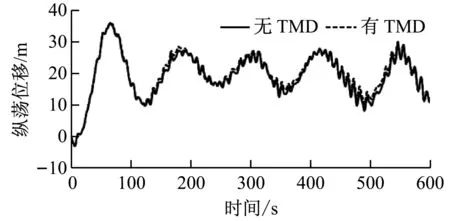
(a) 縱蕩

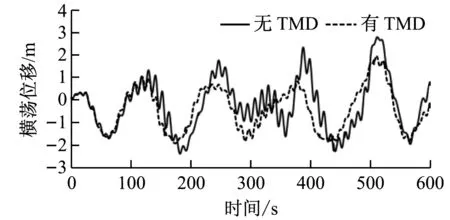
(b) 橫蕩

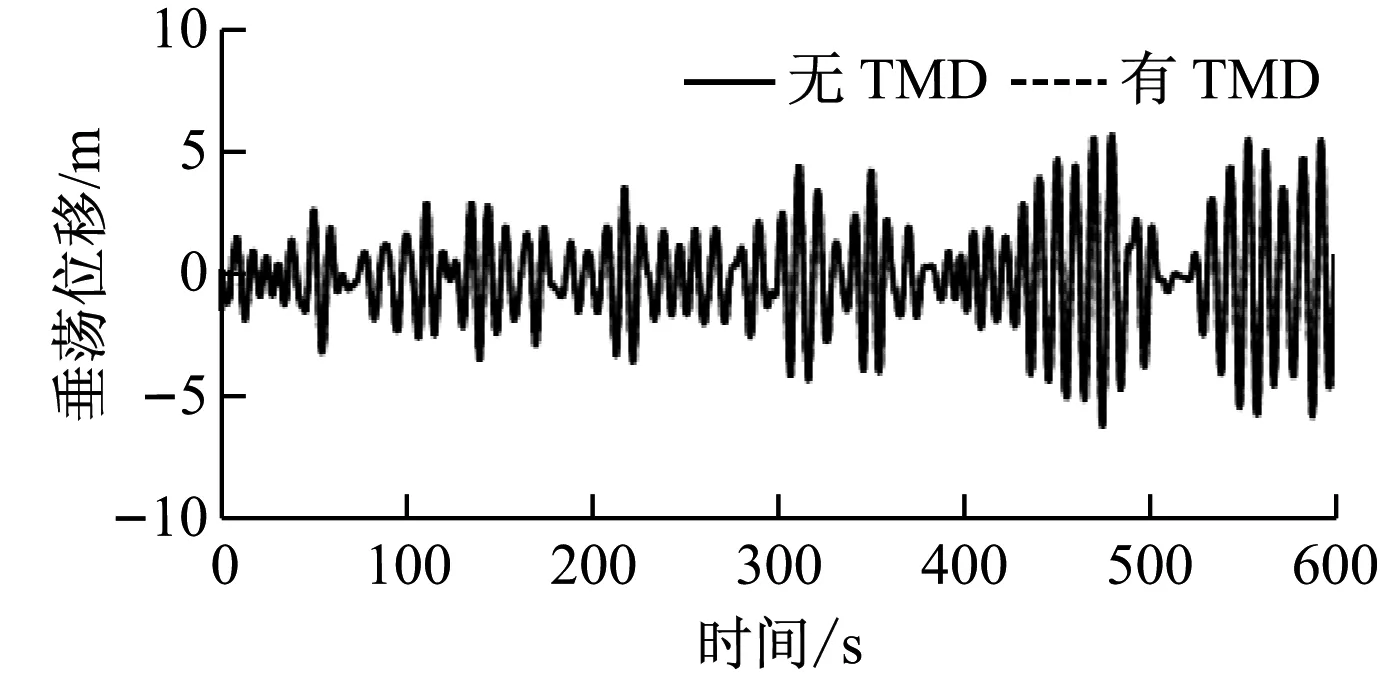
(c) 垂蕩

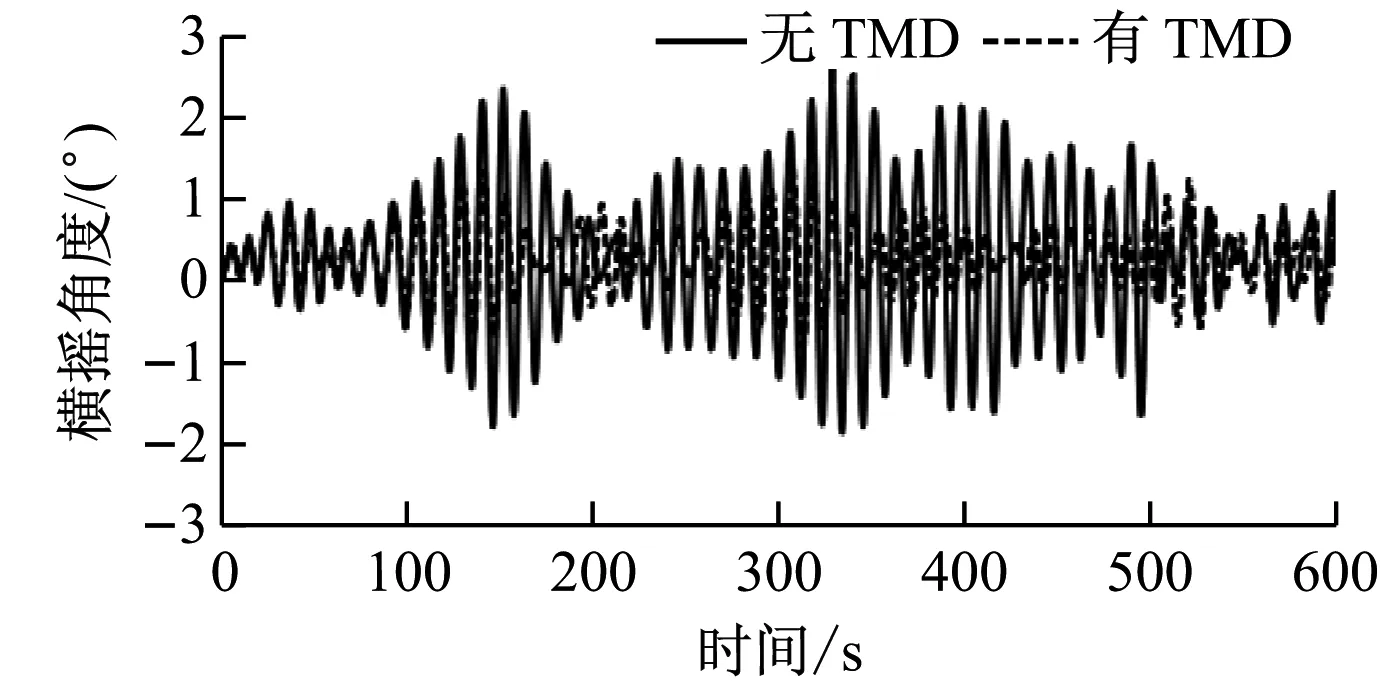
(d) 橫搖

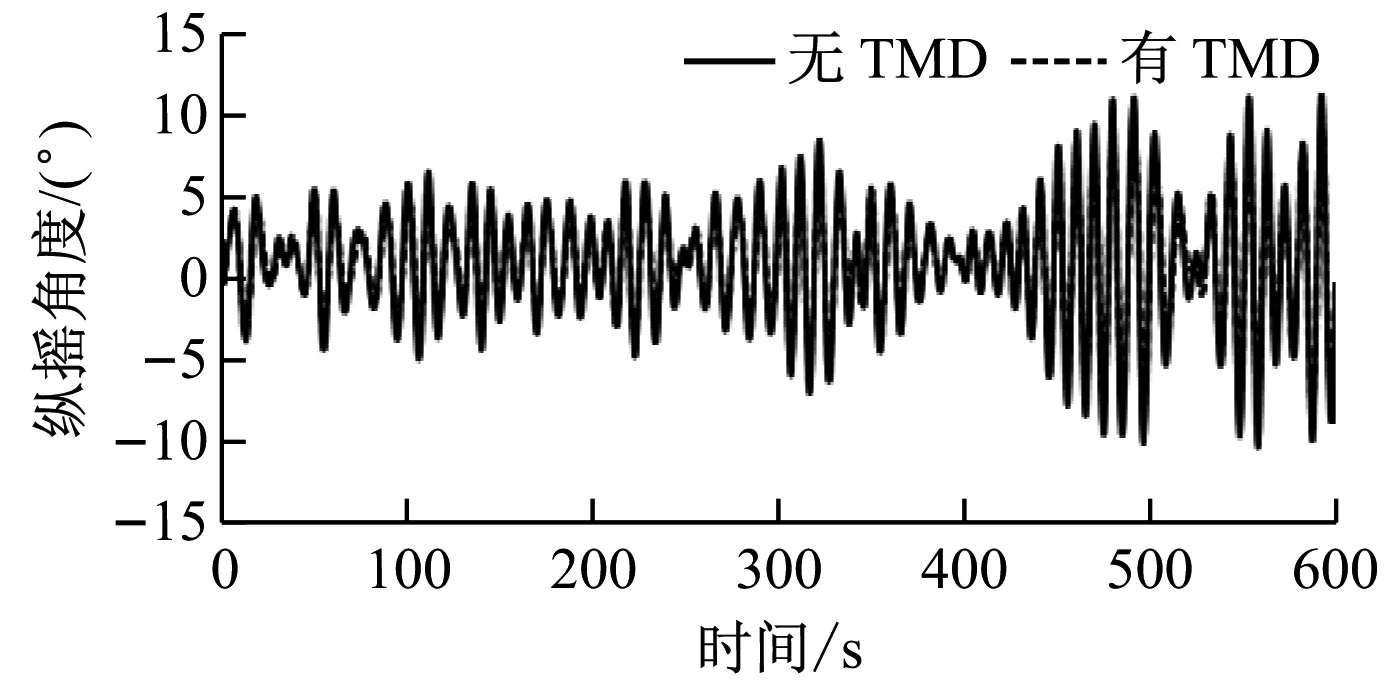
(e) 縱搖

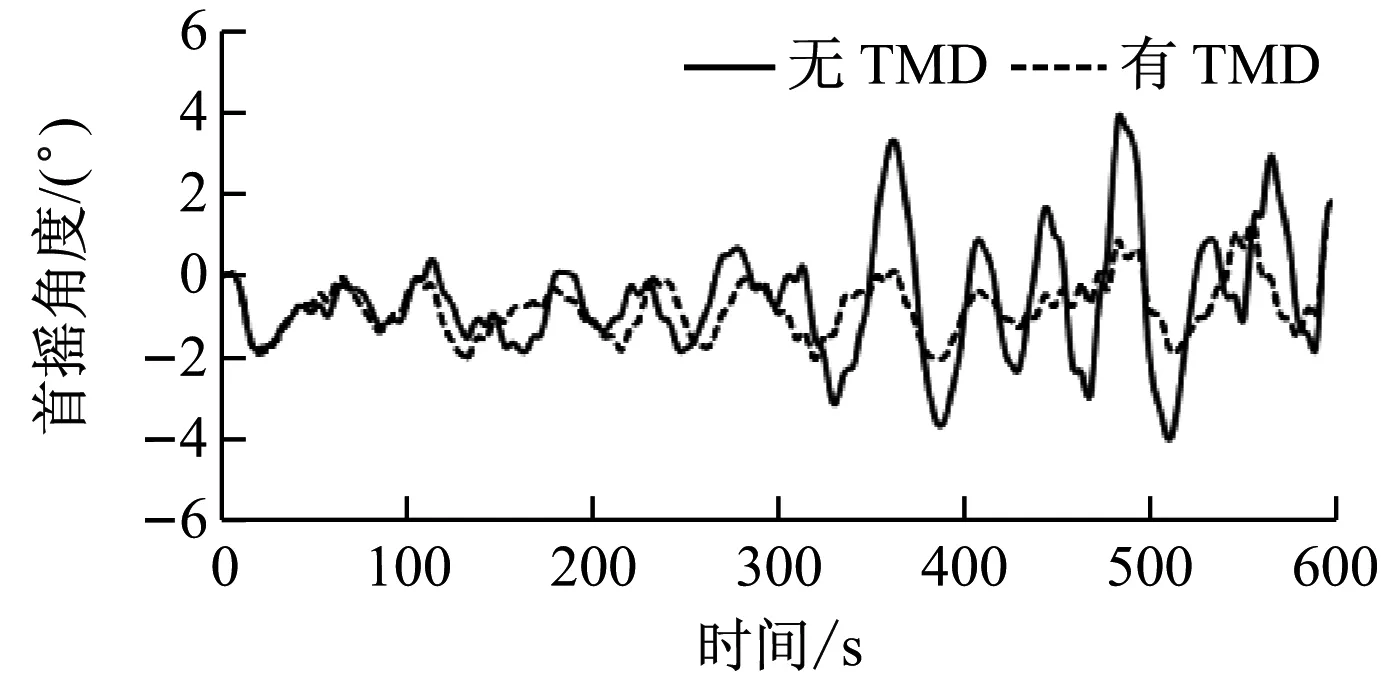
(f) 首搖

由圖8可知，加入TMD控制后，平臺的縱蕩位移、垂蕩位移和縱搖角度變化較小，而橫蕩位移、橫搖角度和首搖角度變化較為明顯。在TMD控制下，平臺的最大橫蕩位移由2.78 m減小至1.96 m，降低了29%，橫蕩位移波動范圍由-2.35～2.78 m減小至-1.92～1.96 m；橫搖最大角度由2.38°減小至1.32°，降低了45%，橫搖角度波動范圍由-2°～2.38°減小至-1°～1.32°，減幅明顯；首搖角度的變化規律不明顯。有、無TMD控制時平臺橫蕩位移標準差分別為0.851和1.034，在TMD控制下穩定性提高了18%；有、無TMD控制時平臺橫搖角度標準差分別為0.541和0.917，在TMD控制下穩定性提高了41%。由于平臺縱蕩、垂蕩和縱搖的變化不明顯，且首搖變化規律不明顯，故僅給出橫蕩與橫搖的幅值譜，如圖9所示。

由圖9可知，平臺橫蕩和橫搖的頻譜峰值對應的頻率分別為0.01 Hz和0.09 Hz;加入TMD控制后平臺的橫蕩幅值從0.23減小至0.14，降低了39%；加入TMD控制后橫搖幅值從0.19減小至0.12，降低了36%，減幅均較明顯，說明TMD控制對平臺橫蕩和橫搖的控制效果顯著。

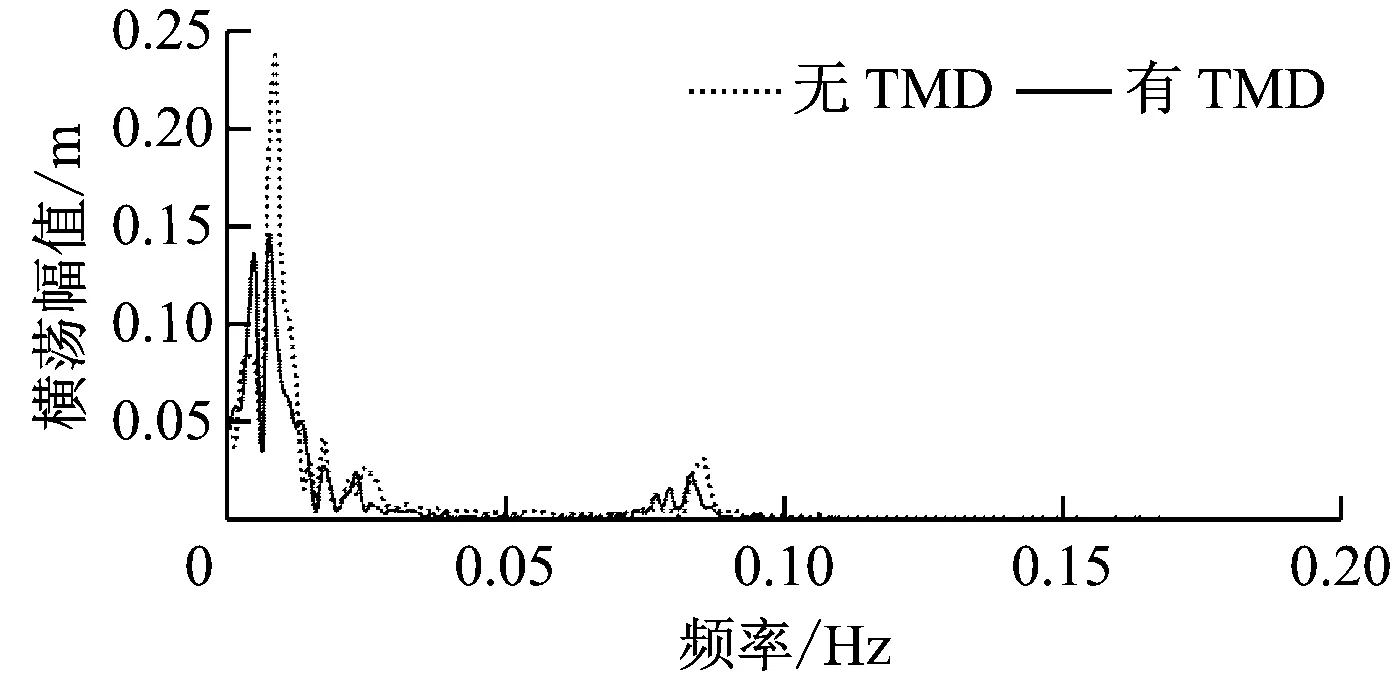
(a) 橫蕩

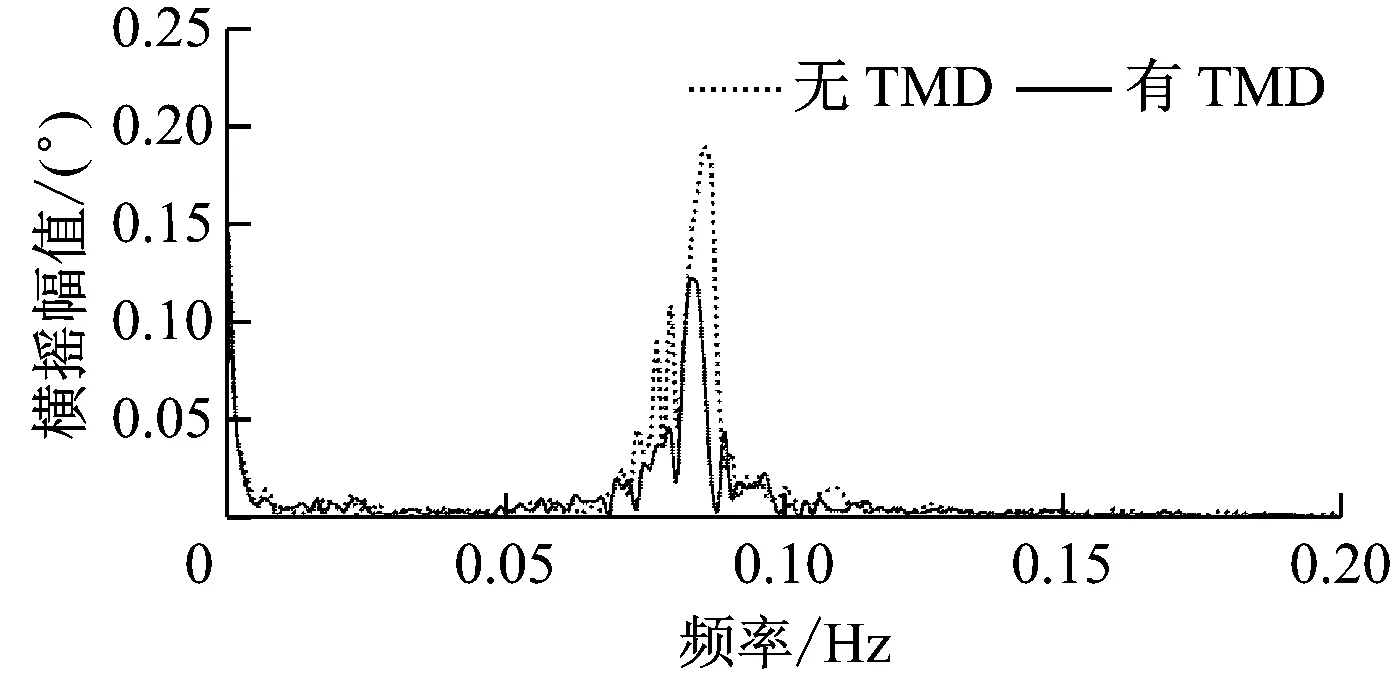
(b) 橫搖

5.2 TMD對塔頂位移的影響

漂浮式風力機在TMD控制下的塔頂位移時歷曲線如圖10所示。由圖10可知，漂浮式風力機在無TMD控制情況下，開機前塔頂前后位移在-1～1 m內較為規律地波動；在開機(大約70 s)后，塔頂側向位移以約150 s的周期運動。在TMD控制下，塔頂前后位移基本不變。在無TMD控制下，塔頂側向位移在-0.09～0.06 m之間波動，在TMD控制下僅在-0.06～0.02 m之間波動，側向位移明顯減小，其最大值降低了66%。在有、無TMD控制下塔頂側向位移的標準差分別為0.030和0.048，即有TMD控制后塔頂側向位移標準差降低了38%。塔頂位移幅頻特性曲線如圖11所示。塔頂前后及側向位移的頻譜峰值分別在0.06 Hz和0.08 Hz附近。無TMD控制時塔頂前后及側向位移幅值均大于有TMD控制時的幅值，但塔頂前后位移幅值變化較小，而側向位移幅值減小明顯。

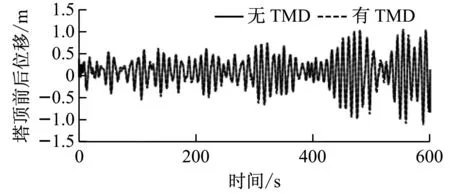
(a) 塔頂前后位移

(b) 塔頂側向位移

Fig.10 Time-history curve of back-and-forth displacement of the tower top

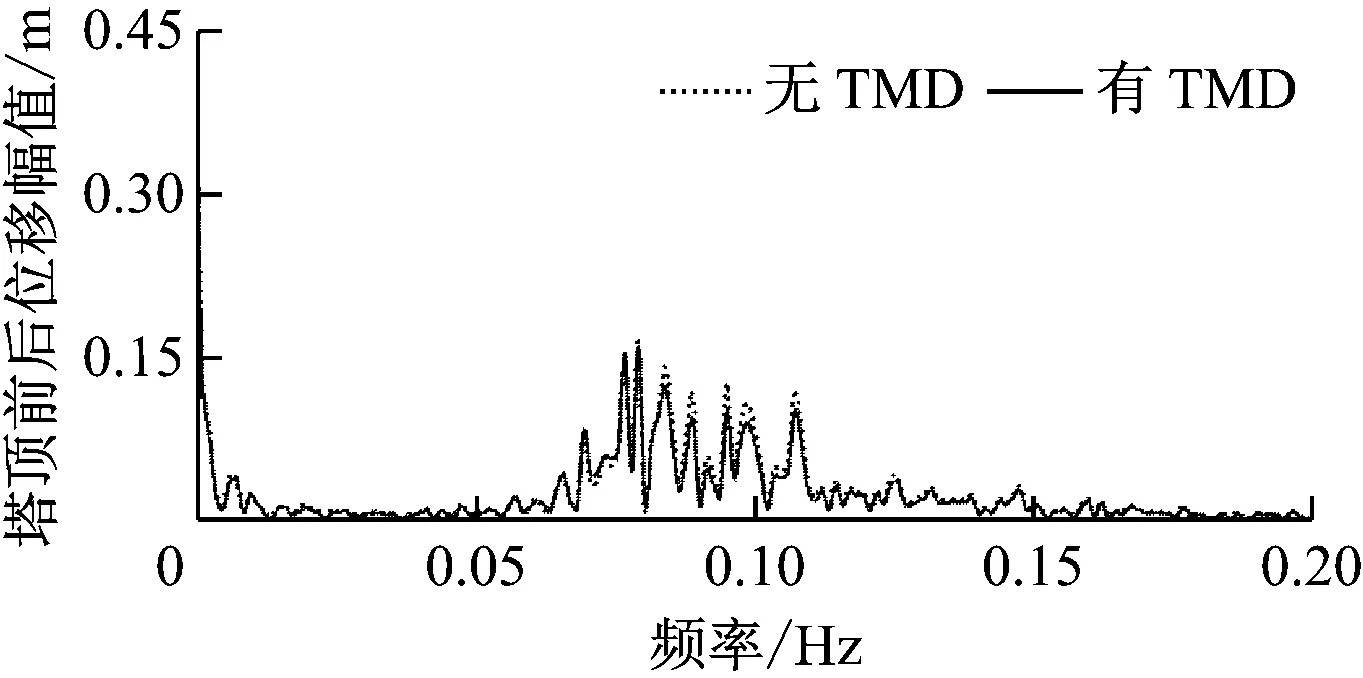
(a) 塔頂前后位移

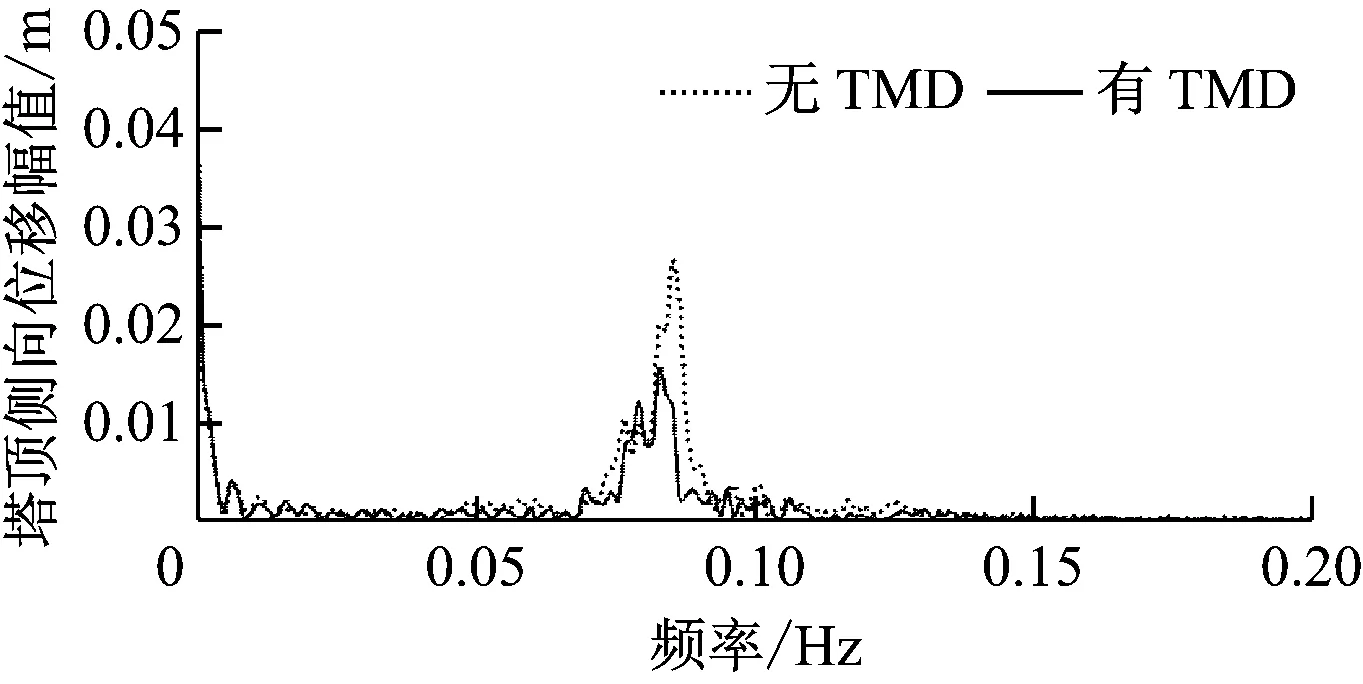
(b) 塔頂側向位移

Fig.11 Amplitude-frequency response curve of back-and-forth and lateral displacement of the tower top

6 結 論

(1) 在TMD控制下，漂浮式風力機平臺橫蕩和橫搖降幅明顯，其最大值分別降低了29%和45%，穩定性分別提高了18%和41%。

(2) TMD控制對漂浮式風力機塔頂前后位移的控制效果不明顯，對塔頂側向位移的控制效果較明顯，其最大值降低了66%，穩定性提高了38%。