基于小波能譜熵和集成經驗模態分解的傳感器故障診斷耦合算法研究
史歷程, 趙 驍, 趙群飛, 王玉璋
(1. 上海交通大學 機器人視覺與圖像測控實驗室, 上海 200240; 2. 中國航空發動機集團沈陽發動機設計研究所, 沈陽 110015; 3. 上海交通大學 燃氣輪機研究院, 上海 200240)
燃氣輪機是各類航空噴氣發動機及其衍生燃氣輪機、重型發電燃氣輪機、車輛與工業驅動燃氣輪機、艦船動力燃氣輪機及各種微型燃氣輪機的總稱[1],具有啟動快、效率高、運行平穩的特點,在航空、航海和發電系統等領域得到了廣泛的應用。航空和艦船用燃氣輪機具有啟停頻繁、運行工況復雜和運行環境復雜等特點。而發電系統用燃氣輪機要求長時間穩定運行、長壽命、低維護成本等。
為了保證燃氣輪機安全穩定運行,需要使用各種類型的傳感器進行監控,而傳感器輸出信號的實時性、準確性和可靠性直接影響發動機的控制和安全,一旦傳感器發生故障,后果十分嚴重。燃氣輪機結構復雜,工作環境惡劣,所需要的傳感器種類很多,其敏感元件容易受到各種干擾,其非平穩性、非線性度很高[2],所需測量的參數(如溫度、壓力等)范圍大,傳感器信號具有維度高、穩定性差和非線性度高等特點。由此可見,研究高效、可靠、快速的傳感器故障診斷算法,對于燃氣輪機高效可靠運行、降低檢修維護成本具有重要的意義。
傳統的信號分析方法如傅里葉變換,很難對這種非平穩特征的數據進行分析,而且也很難對數據在時域和頻域進行精確分析。針對傳統方法對傳感器故障診斷方面的不足,近年來國內外學者進行了大量的研究。Zhao等[3-5]提出了基于小波變換的故障診斷方法,通過小波變換來實現傳感器的故障檢測,雖然一定程度上解決了傳感器故障診斷問題,但也存在局限性。小波變換一旦選定基函數,轉換特性固定,其適應性較差,對多種類型傳感器信號的診斷有一定的局限性。為了得到適應性更好的故障診斷算法,一些學者嘗試利用人工智能領域的思想來解決問題。朱嶸嘉等[6]采用模糊邏輯來實現燃氣輪機氣路單一故障診斷,通過建立故障診斷的模糊數學模型和模糊診斷矩陣,依據模糊診斷矩陣和最大隸屬原則進行燃氣輪機的故障診斷,在故障表征與原因之間建立模糊關系,由隸屬度大小來檢測燃氣輪機故障,在實際的燃氣輪機故障檢測中有可靠合適的檢測精度,但其自學習、自更新能力不強,很難應用到更廣泛的范圍內。神經網絡[7-9]作為近年來人工智能領域的研究熱點,廣泛應用于故障類型的分類,但其存在易陷入局部最小點和過學習等問題。支持向量機(SVM)作為一種特殊的單層神經網絡非線性分類模型,劉靜雅等[10-11]將其應用在信號故障診斷領域,針對不同故障類型的監測數據建立不同的分類器模型,實現對燃氣輪機部件傳感器信息的故障診斷,但SVM分類器需要多個二分類器組合實現多分類,且需要優化合適的核參數與懲罰因子才能獲得滿意效果。上述基于殘差的分類模型,其殘差物理本質反映不明顯,往往不具有客觀性。為了獲取信號的本質特征,增強診斷算法的客觀性, Dang等[12-13]通過經驗模態分解(EMD)對信號進行分解,獲得固有模態函數(IMF)和殘余分量,并將其能量及信號削減比組成等特征構成特征向量進行故障診斷。但由于EMD存在模態混淆現象,使分解的穩定性降低,在一定程度上影響了后續特征提取效果。陳寅生等[14]介紹了一種利用噪聲輔助方法來抑制EMD的模態混淆現象,引入表示信號產生新信息的速率的樣本熵(SE)來反映信號本質的特征向量,并采用通過稀疏表示分類(SRC)進行信號故障的分類方法,成功提高了故障診斷的準確率,并在一定程度上增強了算法的自適應性。不過由于需要對信號進行預處理,且增加了信號復雜度,這種方法比原始EMD的分解時間更長,有時不能滿足燃氣輪機的實時性要求。
筆者提出一種基于多特征提取與故障分類診斷的耦合算法,并建立燃氣輪機狀態監測及故障診斷系統,可通過振動、位移、轉速、溫度和壓力傳感器所集成的傳感器監測網絡進行實時采集及信息提取,運用集成經驗模態分解(EEMD)計算樣本熵,利用小波分解來計算小波熵等方法進行故障提取。同時根據故障模式與傳感器類型的不同,采用不同的故障分類識別方法進行燃氣輪機故障的綜合診斷,使燃氣輪機健康管理系統具有精確的實時狀態監測和全面準確的故障診斷功能。
1 基本原理
1.1 小波函數形式
小波分析的核心是利用小波變換對信號作出分解并進行分析,其基本思想是用一簇函數來表示或逼近一信號或函數。

(1)
式中:Cψ為ψ(t)的允許性條件。
則ψ(t)為一個基本小波函數,簡稱為小波。
通過伸縮和平移,該函數可生成一簇小波函數,稱為小波序列:
(2)
式中:a為尺度參數;b為定位參數。
ψa,b(t)的離散小波變換定義為:
(3)
式中:a0、b0分別為a和b的離散值;k為離散變換系數;j∈Z。
1.2 小波能譜熵(WEE)
小波能譜熵是小波分析理論與熵原理的結合,充分發揮了二者的優點,既能達到信息融合的目的,又能更有效地分析突變信號,能更好地適應信號的特征提取。小波能譜熵的計算步驟如下。
將任意信號x(t)向不同尺度的小波空間投影,則可得到不同尺度下的細節信號:
(4)
式中:Cj(k)和dj(k)分別為低頻分量系數和高頻分量系數。
設時間序列長度為N,則信號x(t)在第j層k時刻各小波變換的結果可表示為:
D={Dj(k)},k=1,…,N,j=1,…,J
(5)
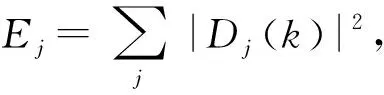
根據小波變換系數在不同尺度內的能量分布情況,可計算出信號在不同尺度的小波能譜熵:
(6)
1.3 集成經驗模態分解
EEMD方法從本質上講是對一個信號進行平穩化處理,其結果是將信號中不同尺度的波動或趨勢逐級分解開來,產生一系列具有不同特征尺度的數據序列(即IMF)。
EEMD方法的計算步驟[14]如下:
(1) 將一定幅度的高斯白噪聲n(t)疊加到原始信號x(t)上,生成新信號:
x(t)=x(t)+n(t)
(7)
(2) 對信號反復進行EMD分解,得到IMF集合:
x(t)=[{c1(t)}, {c2(t)}, …, {cJ(t)}]
(8)
式中:cJ(t)為第J次EMD分解得到的IMF分量。
(3) 將該集合進行總體平均,獲得EEMD分解得到的IMF分量,原始信號x(t)經過EEMD 分解后的結果為:
(9)
式中:r(t)為經過EEMD分解后的剩余分量。
IMF分量反映了原始信號的特征尺度,代表著非線性、非平穩數據序列的本征模態特征,通過分析IMF分量的特征,便可推知原數據序列的特征信息。樣本熵是一種時間序列復雜性測度方法,表示時間序列產生新信息的速率,這與傳感器故障信號的產生形式一致,一般來說,信號越復雜,樣本熵越大。樣本熵的計算步驟如下:
(1) 將N點時間序列x(i)按序號組成一組m維矢量:
x(i)=[x(i),x(i+1), …,x(i+m-1)],
i=1,2,…,N-m+1
(10)
(2) 定義矢量x(i)與x(j)之間的距離為最大坐標差,按序號組成一組n維矢量:
d[x(i),x(j)]=max[|x(i+k)-x(j+k)|],k=1,2,…,m-1,i=1,2,…,N-m+1
(11)
(3) 對于給定相似容限r,統計第i個向量與其他N-m個向量之間的距離小于r的數目,并計算其與N-m的比值,記為:
(12)
式中:Θ為Heaviside函數。

(13)
(5) 增加矢量維數為m+1,通過重復上述計算步驟,得到Cm+1(r)。
(6) 時間序列x(n)的樣本熵為:
(14)
當時間序列長度N為有限值時,上式可轉化為:
(15)
2 2種算法的比較與融合
2.1 操作系統與數據集
基于LabVIEW平臺,實現了各路傳感器性能狀態參數在線采集、綜合分析和整機診斷的功能。以某燃氣輪機機組為研究對象,得到其17路傳感器運行數據,每路傳感器有51 055個數據,將80%的運行數據作為訓練樣本,20%的運行數據作為測試樣本。圖1給出了幾路具有代表性的傳感器信號的波形圖。由圖1可以看出,各傳感器由于測量部件的工作原理、位置及工況的不同,無論其量綱、信號大小還是模式都有很大差異,憑借傳統的故障診斷算法很難對各類傳感器進行統一診斷。
傳感器輸出信號主要存在以下幾種典型故障形式:開路故障、短路故障、階躍故障、脈沖故障、周期故障、漂移故障和噪聲干擾等[10],信號具體特征如圖2所示。將故障信號分別疊加到各傳感器模擬采集的原始信號中,即可得到最終采樣信號。

(a) 燃油反饋

(b) 導葉電流

(c) 大氣溫度

(d) 滑油供油溫度

(e) 計量閥控制前油壓

(f) 壓氣機出口壓力
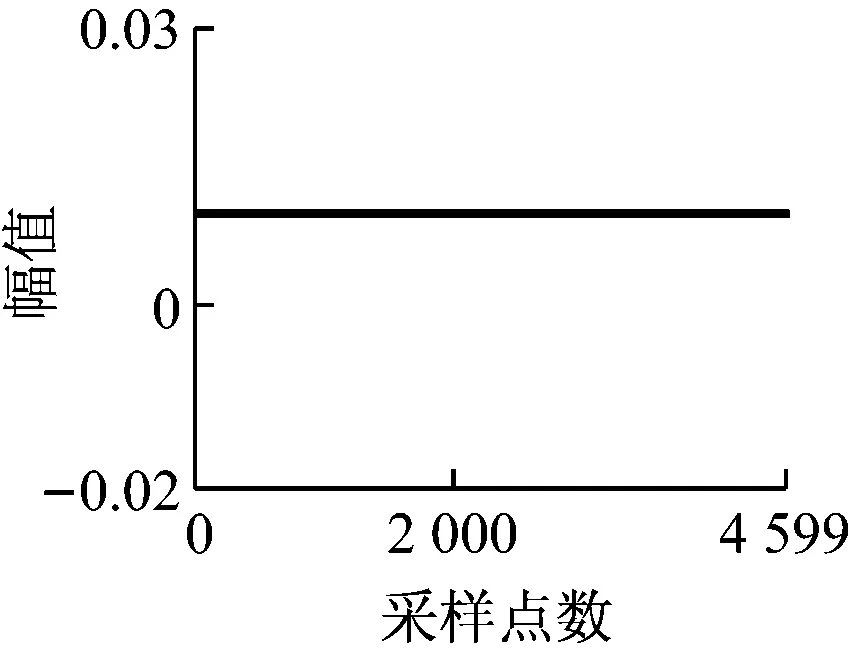
(a) 無故障

(b) 開路故障
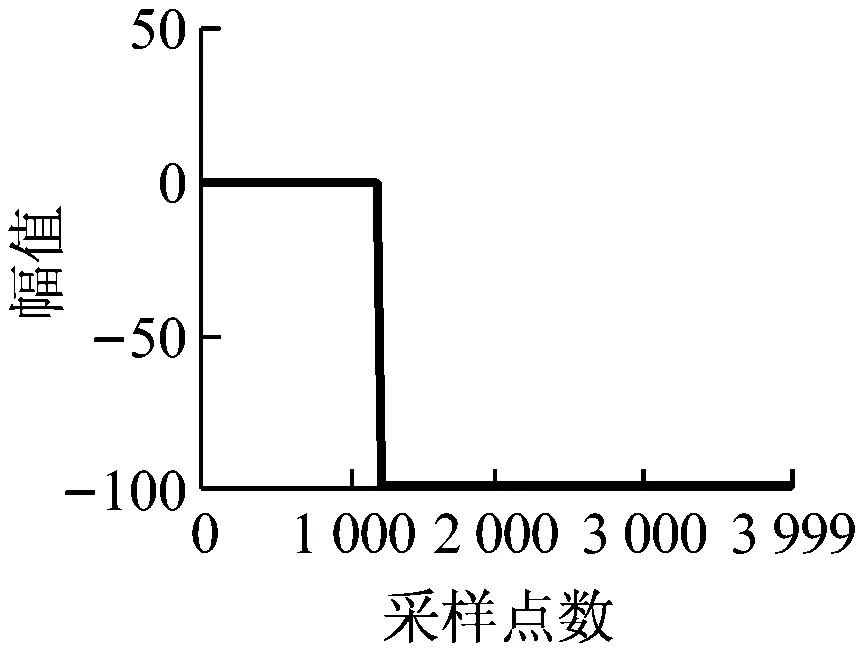
(c) 短路故障

(d) 階躍故障

(e) 脈沖故障

(f) 周期故障

(g) 方差突變故障
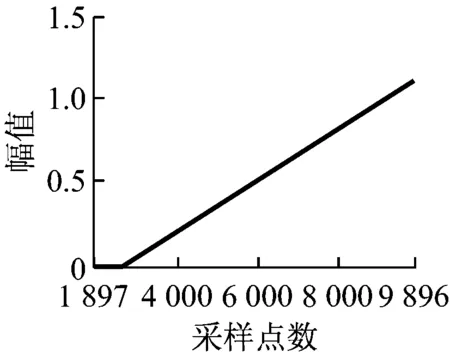
(h) 漂移故障
2.2 特征提取
為了評估所提取的特征向量對各故障類型的可分性,筆者提取了傳感器各種故障狀態下采用不同算法得到的特征向量。表1給出了油壓傳感器處于正常狀態及各種故障狀態下通過WEE方法得到的特征向量。首先構造第1~第5層小波低頻系數與高頻系數,計算其相應的小波能譜熵WEE,并選取各級小波分量的方差σ、均值μ與小波能譜熵WEE組成的向量來構成最終的特征向量。由表1可知,傳感器在不同狀態下經小波熵計算得到的各小波分量包含的故障信息不同,所對應的特征值同樣具有明顯的差異。
將信號樣本進行EEMD 分解。根據總體平均次數選擇方法和加入高斯白噪聲準則,加入高斯白噪聲的幅度A=0.28,期望誤差e設為1%,集成平均次數為100。利用樣本熵分析可以求得每個IMF分量和殘余分量的信號復雜度,從而獲得傳感器故障信號特征向量,用來描述傳感器故障信號的特征。

表1 油壓傳感器不同故障類型下的WEE特征向量
表2給出了油壓傳感器處于正常狀態及各種故障狀態下的EEMD特征向量。信號經EEMD分解后得到4個IMF分量和1個殘余分量。特征值d1~d4為IMF1~IMF4經樣本熵分析得到的樣本熵。特征值d5為EEMD分解后得到的殘余分量樣本熵。由于傳感器在不同狀態下經EEMD分解得到的各IMF分量包含的故障信息不同,所對應樣本熵的特征值具有明顯的差異,展示了良好的故障可分性。

表2 油壓傳感器不同故障類型下的EEMD特征向量
為了更好地分析各類算法的優缺點,考慮到燃氣輪機的應用背景,分別以脈沖信號作為典型的突變型故障,以漂移故障作為典型的緩變型故障,并考慮到不同傳感器信號的測量范圍差異,分別進行信號的傅里葉變換、小波變換、小波熵和EEMD分解仿真實驗,結果如圖3~圖7所示。圖3為平穩脈沖信號的特征提取仿真實驗結果。由圖3可以看出,傅里葉變換后的信號出現了特征值上下振蕩,而小波變換的各層分量則在故障點處出現了特征值的突變,而EEMD同樣在第一層IMF分量中出現了特征值突變,可以認為這些方法在處理平穩脈沖信號時都可以進行準確的診斷。


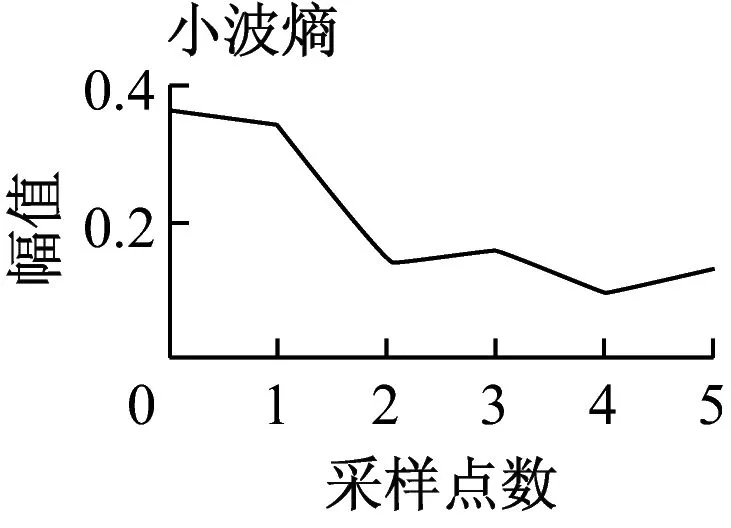









圖3 幅值為40的平穩脈沖信號的特征提取
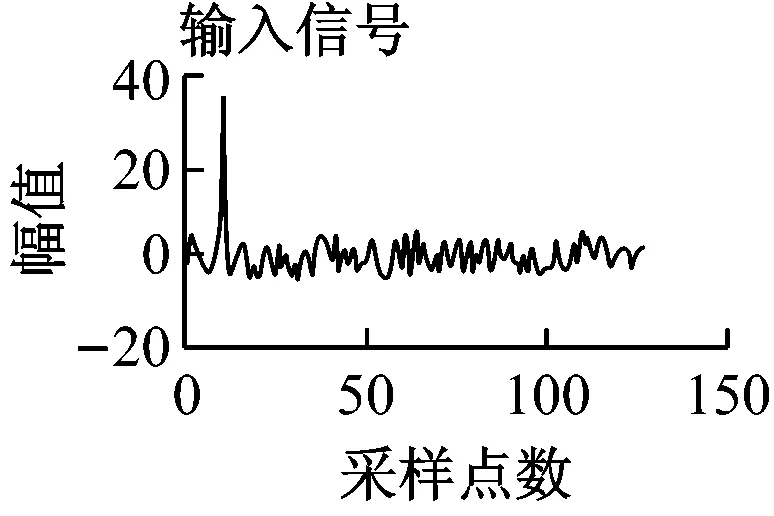



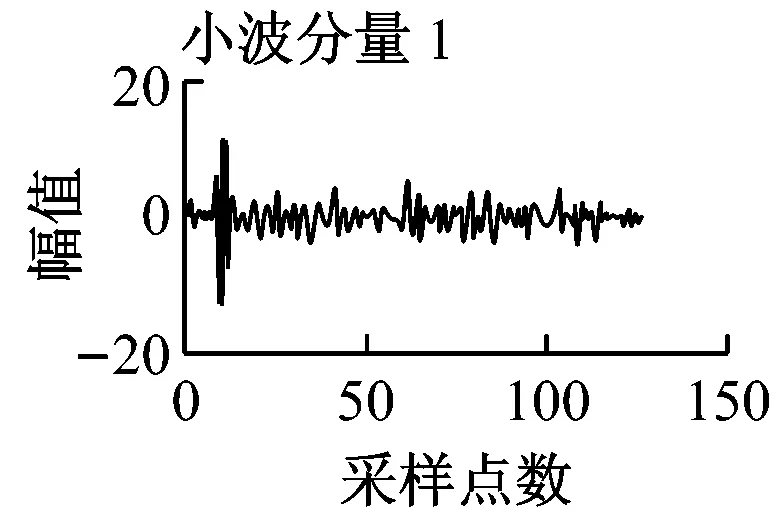

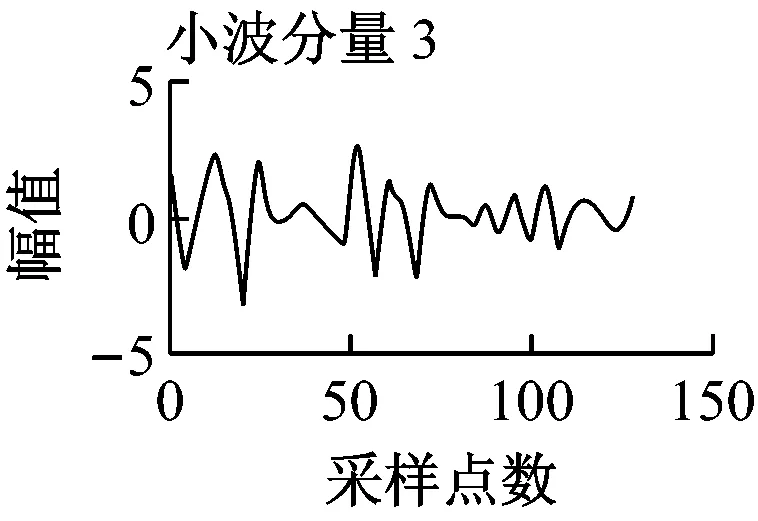





圖4 幅值為40的非平穩脈沖信號的特征提取




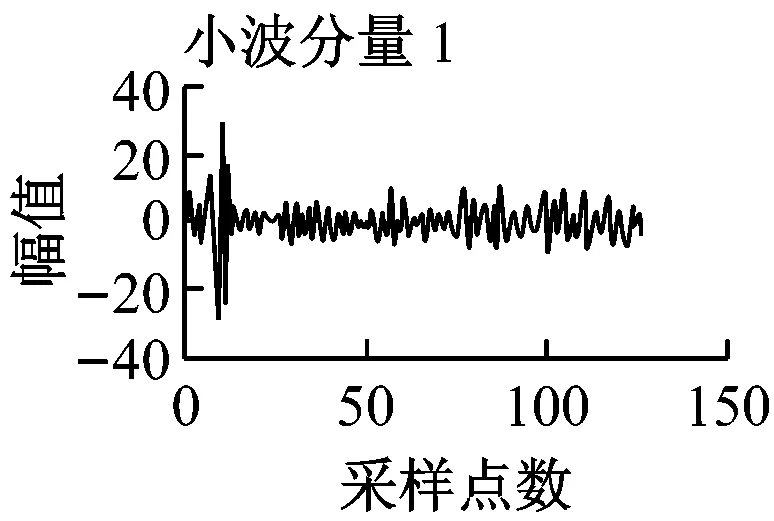
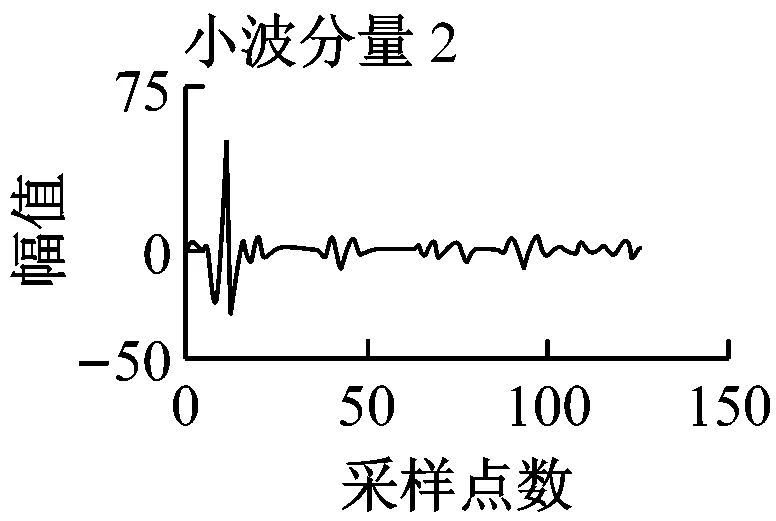






圖5 幅值為100的非平穩脈沖信號的特征提取




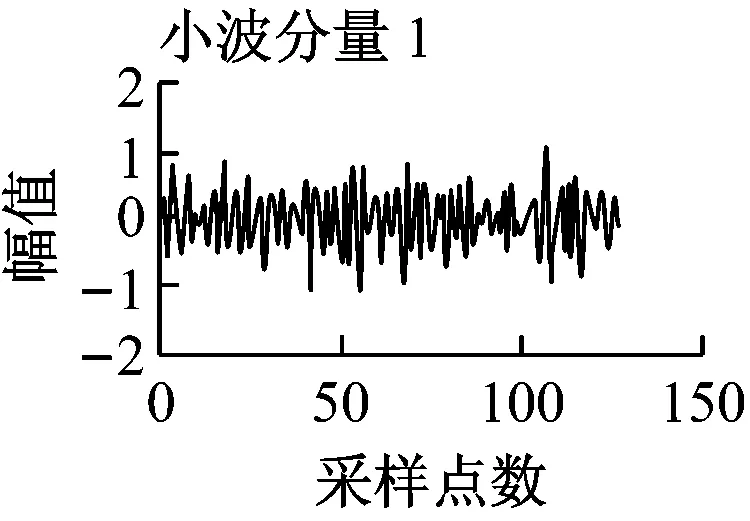







圖6 幅值為10的非平穩漂移信號的特征提取




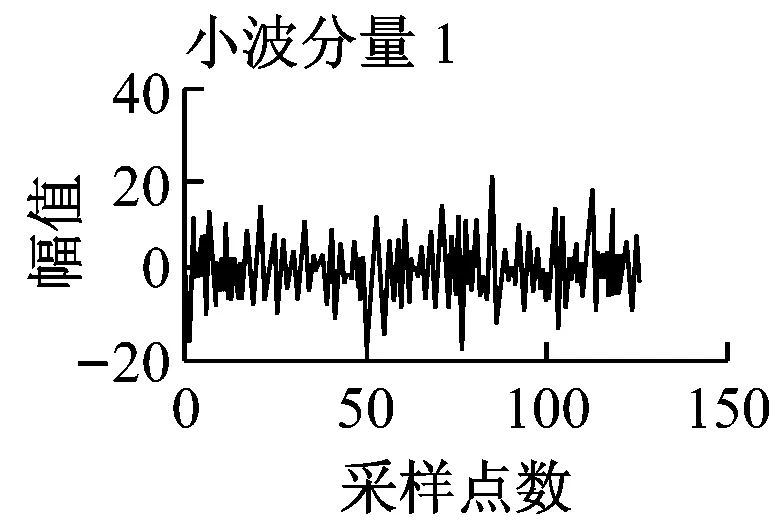





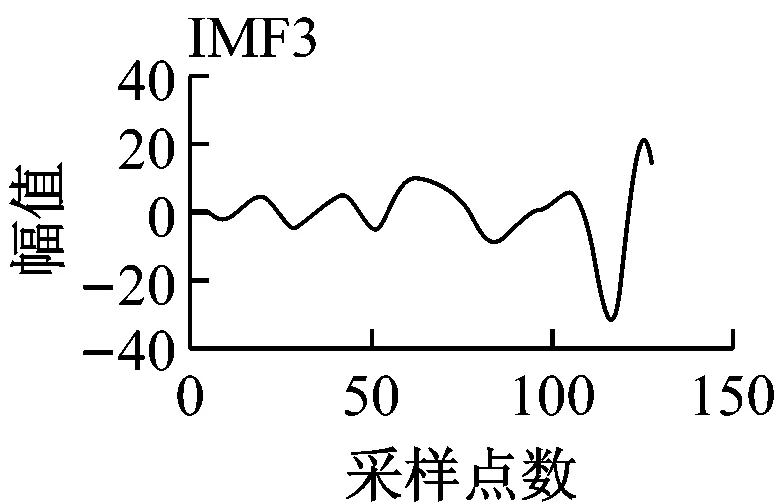
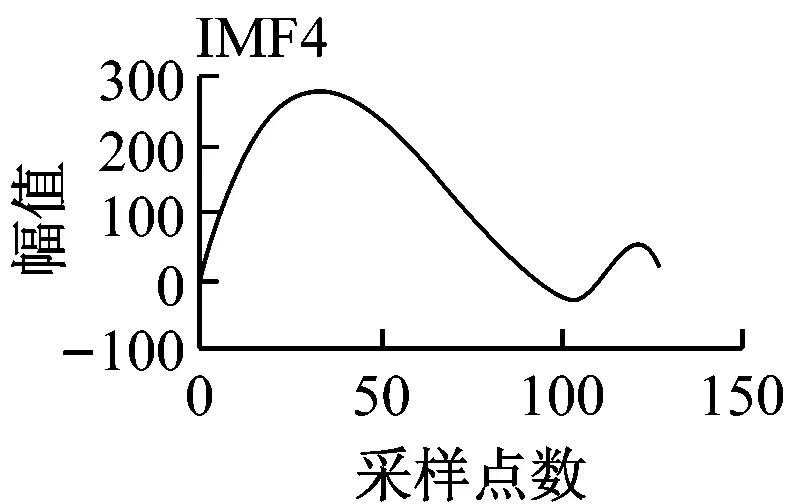
圖7 幅值為100的非平穩漂移信號的特征提取
圖4為非平穩脈沖信號的特征提取仿真實驗結果,圖4在圖3中信號的基礎上增加了均值為0、幅值為4的均勻白噪聲。由圖4可以看出,傅里葉變換后的特征值變得雜亂無規律,而其余2種方法都出現了特征值的突變,因而傅里葉變換不適用于非平穩脈沖信號的故障分類。
圖5為幅值為100的非平穩脈沖信號的特征提取仿真實驗結果。由圖5可以看出,在信號測量范圍變大之后,雖然特征值變化曲線與圖4相似,但各層小波分量的尺度大小隨之發生了明顯變化,而利用小波能譜熵提取的小波熵值并未發生明顯變化。這說明利用小波能譜熵進行不同尺度信號的故障分類可以建立一個統一的閾值進行診斷,而傳統的小波變換則不適用。
圖6為幅值為10的非平穩漂移信號的特征提取仿真實驗結果。由圖6可以看出,各層小波特征值并無明顯變化規律,而利用EEMD分解得到的第4層IMF出現了特征值周期性的變化,因此EEMD分解比小波變換更適合于漂移故障的診斷。
圖7為幅值為100的非平穩漂移信號的特征提取仿真實驗結果。由圖7可以看出,雖然信號的尺度變大了,利用EEMD得到的樣本熵值變化并不明顯,因此進一步證明該方法在同種漂移故障不同幅值的識別上具有統一性。
2.3 診斷實驗結果及分析
將數據集中各類傳感器信號作為輸入,并疊加7類故障,樣本熵相似容限r設為0.2,SRC稀疏層參數設為20,每類故障分別診斷20次,統計各類算法平均準確率與所需時間。
表3給出了基于不同特征提取方法和K近鄰(K-Nearest Neighbor,KNN)分類器的傳感器故障診斷的識別準確率結果。由表3可以看出,采用文獻[8]的方法在處理緩變型故障時得到了較好的準確性結果:EEMD有效抑制了模態混疊,其抗噪能力和魯棒性強,可以對傳感器輸出信號進行穩定分解,減少了對特征提取的影響;而相比于小波熵,樣本熵特征提取的物理意義與傳感器故障產生形式一致,更適合對故障信號進行特征提取;SRC分類器自適應能力更強,也更適合對多目標進行分類,因此產生了更高的識別準確率。
表4給出了基于不同特征提取方法和分類器的傳感器故障診斷的實時性結果。由表4可知,小波熵結合KNN分類器得到了最快的診斷時間,這是由于K近鄰分類決策上只依據最鄰近的一個或幾個樣本的類別來決定待分樣本所屬的類別,而SRC分類器需要大量故障信號的原始樣本來建立完備字典,求取稀疏解并計算最小殘差值的類別,其計算量相對較大。另外采用EEMD對信號進行分解時需疊加噪聲信號,這也增大了計算復雜度。

表3 各類算法識別準確率比較

表4 各類算法識別速度比較
2.4 耦合算法實驗結果
耦合算法采用混合式的結構模型,結合傳感器信號參數閾值,對采集到的傳感器數據進行初步診斷,診斷結果正常則再輸入到耦合算法模型中,緩變型故障如周期故障等按照EEMD方法進行故障診斷;而突變型故障如短路故障等則采用WEE方法進行診斷。為了保證2種算法判定的可靠性,引入綜合判定參數,當傳感器滿足一段時間且連續多次診斷為同一類型故障時,算法會判定其發生了該種類型故障,如果不滿足該條件時則不輸出故障結果,其診斷流程如圖8所示。
利用綜合判定模塊獲得2種算法的診斷結果后,再根據不同類型的燃氣輪機傳感器需求,劃分不同的診斷優先級,對于診斷優先級較高的傳感器,采用較快的診斷方法優先處理,而診斷優先級較低的傳感器則隨后處理,并且根據故障類型的不同采用不同的診斷算法,兩者結合最終綜合分析出對應故障結果。耦合算法診斷結構框圖如圖9所示。

圖8 綜合判定故障流程
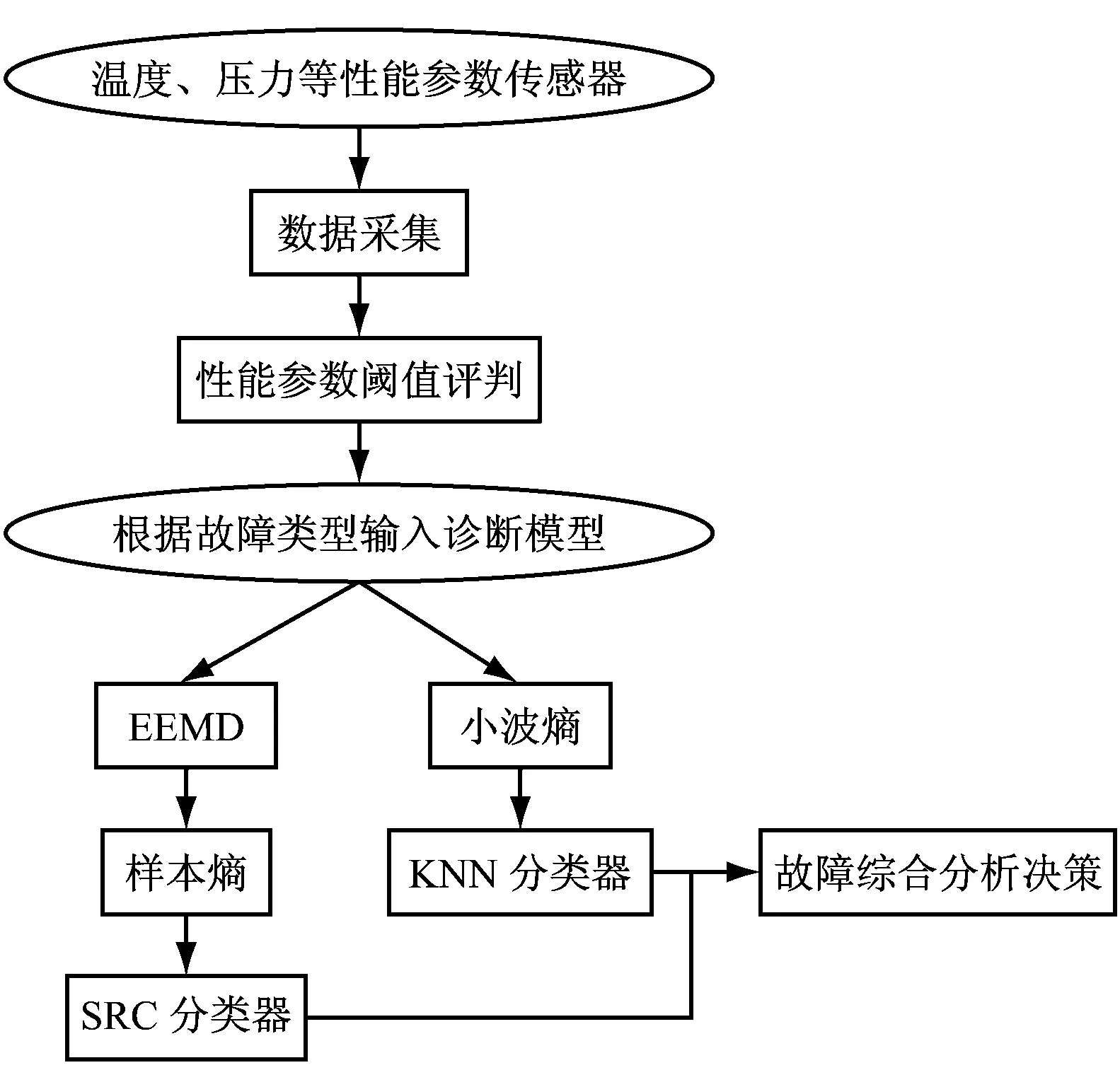
圖9 耦合算法結構框圖
為了驗證耦合算法的診斷效果,選擇所有傳感器信號作為輸入并疊加各類故障各10次,統計平均診斷時間與識別準確率,如表5所示。其中,模擬開路故障診斷檢測結果如圖10所示。
由表5可以看出,將EEMD與小波熵2種算法進行融合,再結合各傳感器工作特性,建立參數閾值輔助進行診斷,與前文提到的算法相比,所提出的耦合算法既提高了故障的識別準確率,同時降低了診斷時間,具有更可靠、快速的診斷效果。

表5 耦合算法識別準確率和診斷時間結果

圖10 模擬開路故障檢測結果
3 結 論
(1) 耦合算法克服了單一或單源傳感器對于機構故障診斷分類的局限性,為燃氣輪機傳感器故障診斷提供了更可靠而全面的結果。
(2) 耦合算法提高了各類故障的識別準確率,其中漂移故障的識別準確率達到97%,其余各類故障的識別準確率最低也達到了91%。
(3) 耦合算法提高了故障診斷的識別效率,對速度要求高的故障類型(如短路故障和脈沖故障等)所需診斷時間降低至0.4 s以下;對需要長時間、多樣本識別的故障類型(如周期故障等)的診斷時間降低至3.07 s,達到了實際過程中控制系統對故障診斷的實時性要求。

