風電機組串聯系統維修方法的研究
謝魯冰, 芮曉明, 林瑜茜, 霍明慶
(華北電力大學 能源動力與機械工程學院,北京 102206)
工業技術的發展在帶來經濟繁榮的同時,也引發了能源革命,清潔新能源的開發和利用迫在眉睫。風能作為一種可再生、綠色清潔能源越來越受到全世界的關注[1]。隨著風電機組單機容量的不斷增大,維修費用率的占比呈現逐漸上漲趨勢[2]。風力發電機組變得越來越復雜,故障率隨之提高,所以在追求風力發電的同時,必須考慮其可靠性和可維護性[3]。基于風力發電機可靠性分析的維護決策研究不僅在安全性方面至關重要,而且從經濟效益的角度看也很重要。
多部件預防維修的原理大致可以分為3類:基于時間的計劃型維修、基于狀態的視情型維修和隨機狀態下的機會型維修[4]。
對于陸上風電機組,由于起步較早,運維已經趨于成熟化。Mathew等[5]針對風力機壽命監測系統的優化,通過基于狀態維修與基于機會維修的優化策略相結合的方式,論證了優化策略的選擇對于壽命監測系統準確性的有效作用;Baidya等[6]基于模糊層次分析法,構建了風電機組狀態監測模型;Serrano-Gonzlez等[7]在研究風電機組市場化發展方式的過程中,也同樣提出針對關鍵部件的預防性機會維修策略對于降低運維成本以及后續大型風電場的建設和融資可行性分析均具有借鑒意義。
對于海上風電機組,由于海上風能資源豐富,不受陸上風電棄風限電的影響,海上風電開發已經成為全球新能源開發的熱點與前沿[8]。但海上風電開發難度大、建設成本高和技術不成熟等因素已成為限制海上風電發展的主要因素,同時海上惡劣多變的風浪條件、備品備件的管理優化和技術人員的資質水平等諸多因素均加劇了海上風電維修的困難性和復雜性。Sarker等[9]建立了基于海上風機組件的多層次機會維修費用率模型,采用機會更換、機會維修以及故障維修同時進行機會維修的方式來降低維護費用率;劉璐潔等[10]考慮到海上風電機組所處的特殊運行環境,針對其運行維護時的等待問題,提出了基于可靠性和維護優先級的預防性維護策略;Shafiee等[11]考慮海上備品備件的后勤管理,并結合海上風浪條件,提出了基于運行狀態與預防性機會維修策略;Ambuehl等[12]以降低海上風電機組風險度和提高可利用度為目標,引入海上風電天氣因素的靈敏度分析,提出了基于狀態維修的優化策略。
上述研究提出了諸多關于風電機組預防維修的方法,但是在對風電機組進行實地考察后,發現具體實施過程中,存在一些不夠完善的方面:(1)在選擇維修方式時出現偏差,導致錯過最佳維修時機;(2)維修過程中存在 “維修欠缺”和“維修過度”的現象;(3)維修過程系統將出現可用度偏小而維修費用率偏大的情況[13]。
針對以上問題,筆者以風電機組串聯系統為研究對象,分別以維修費用率最小、可用度最大及綜合考慮兩方面因素建模,對風電機組的計劃型和機會型預防維修方法進行對比研究。
1 模型建立
將雙饋異步式風電機中齒輪箱和高速軸簡化為一個串聯系統。假設預防維修周期間隔變化,利用可靠度表征隨機故障,同時保證串聯系統存在可靠度下界,分以下3個部分來建模[14]:(1) 以風電機組串聯系統維修費用率最小為目標進行建模;(2) 以風電機組串聯系統可用度最大為目標進行建模;(3)綜合考慮維修費用率最小、可用度最大進行建模。
2 計劃型預防維修模型
計劃型預防維修是指無論系統是否正常工作,基于系統的運行特性直接進行維修的行為。早期的計劃型預防維修以周期性維修[15]為主,近年來隨著維修理論的發展與完善,不完全維修[16-18]開始被引入實踐。
以下分別建立基于維修費用率最小的計劃型預防維修模型(C模型)、基于可用度最大的計劃型預防維修模型(A模型)和綜合考慮維修費用率最小、可用度最大的多目標預防維修模型(U模型)并進行計算分析。
2.1 C模型
2.1.1 模型建立
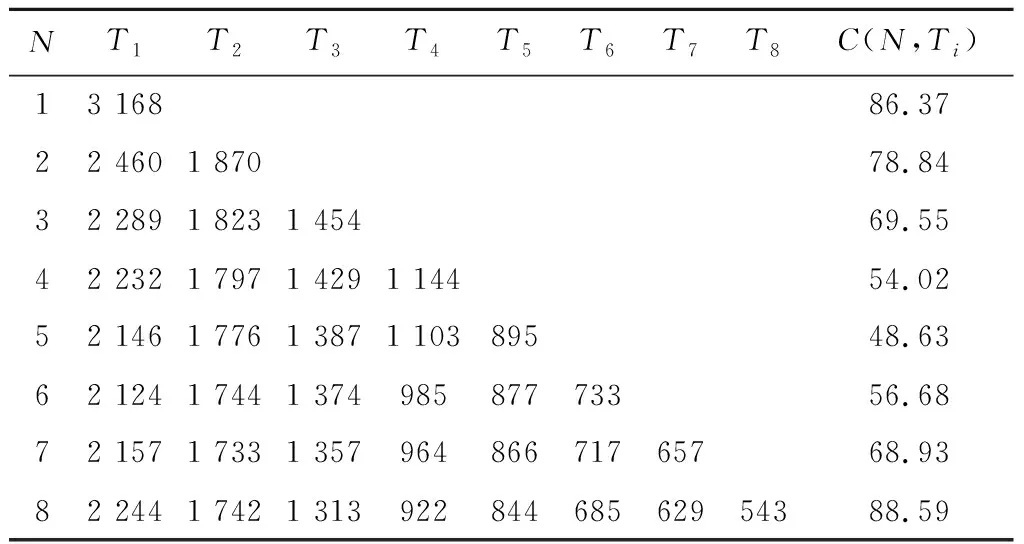
齒輪箱F1在進行第i次預防維修時出現故障問題的平均次數為初始故障率函數對預防維修周期長度的積分:
(1)
高速軸F2在進行第i次預防維修時出現故障問題的平均次數為故障率對預防維修周期長度的積分:
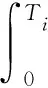
(2)
一個周期內維修費用率為:
(3)
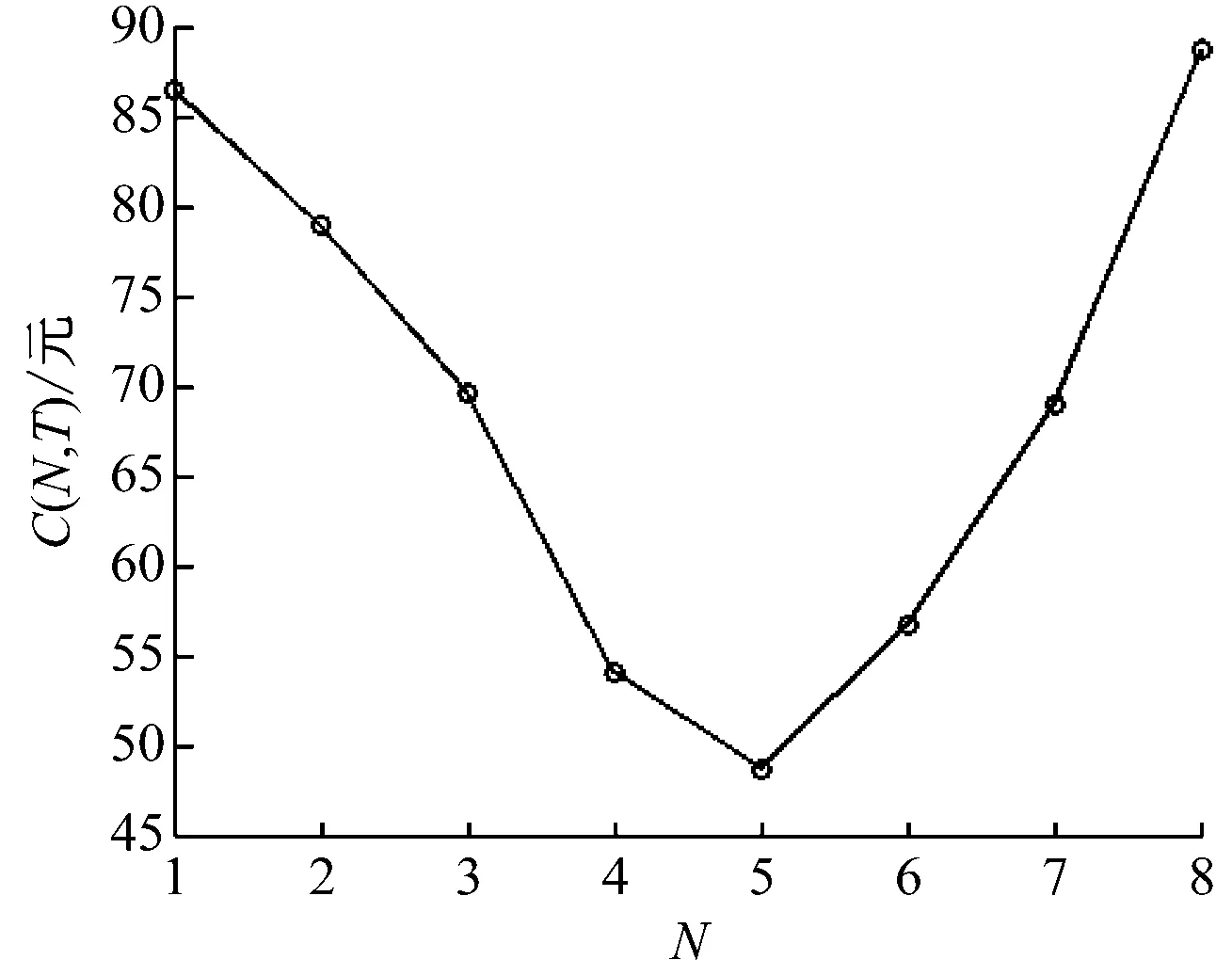
齒輪箱F1在第i次預防維修周期結束時的可靠度為:
(4)
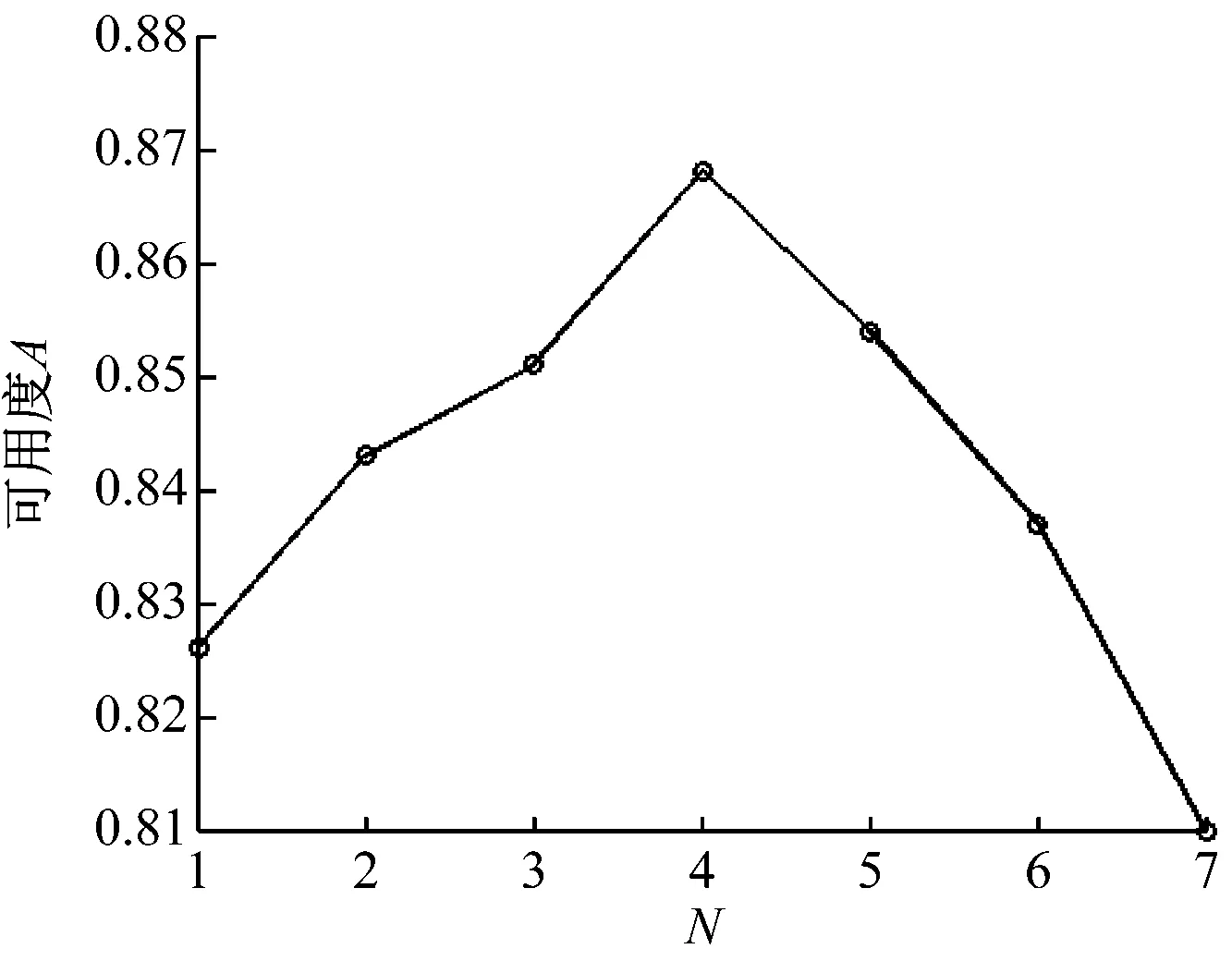
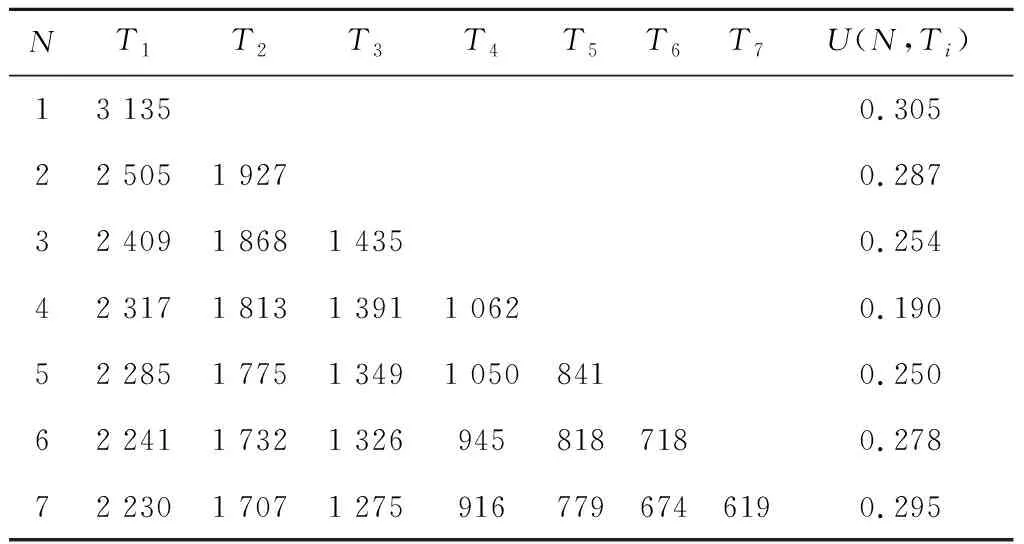
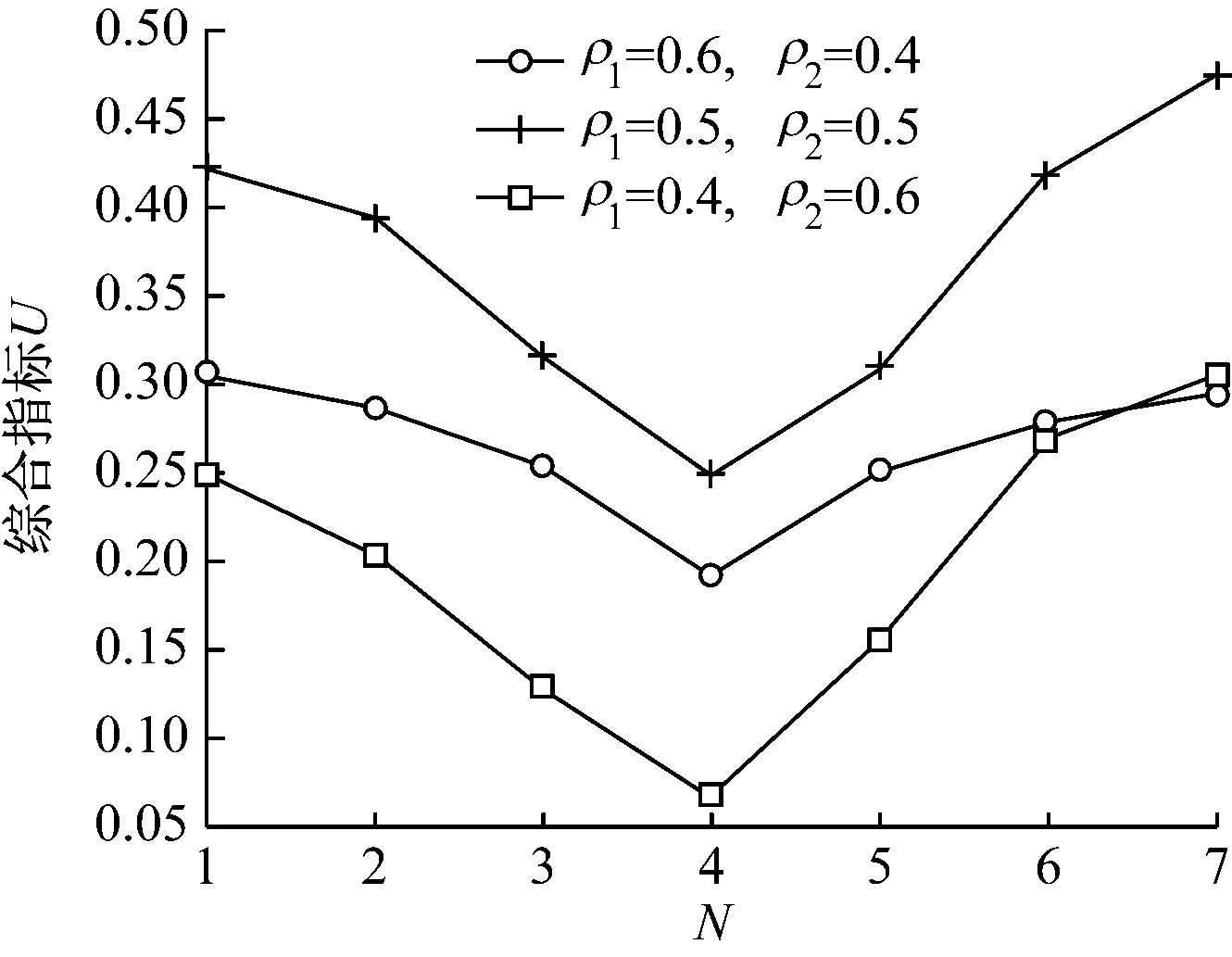
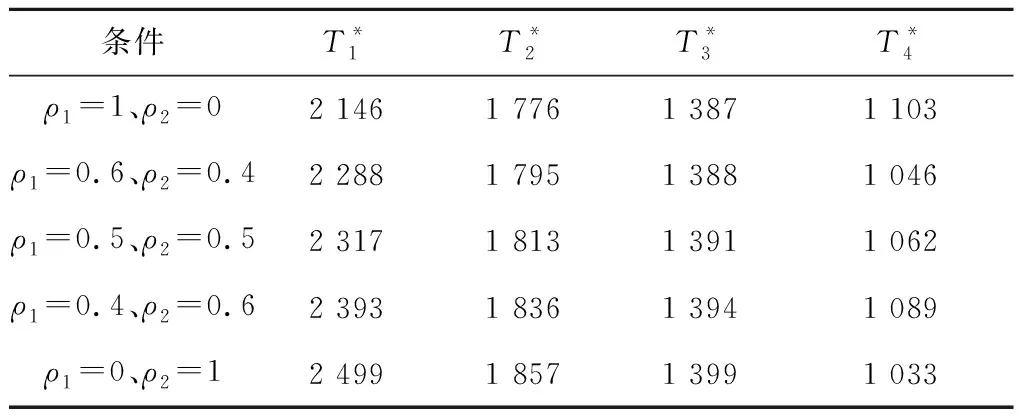
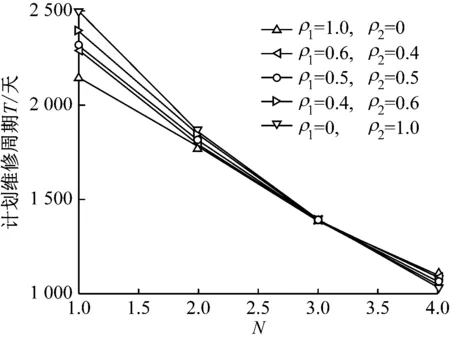
其中:0 串聯系統維修費用率最小的計劃型預防維修模型為: (5) (6) 式中:c1為對F1進行一次故障小修所需費用;c2為對F2進行一次故障維修所需費用;c3為對F2進行一次故障維修時,給F1帶來的額外費用;c4為對F1進行一次計劃預防維修所需費用;c5為對F1進行維修的同時對F2檢修一次所需費用;t1為對F1進行一次故障小修時機組的停機時間;t2為對F2進行一次故障維修時系統停機時間;t3為對F2進行一次故障維修時,拆裝F1花費的停機時間;t4為對F1進行一次計劃預防維修時機組的停機時間;r(t)為F1的初始故障率函數;ω為F2的故障率;x為組件的役齡回退因子[19],0 2.1.2 分析求解 風電機組選型參考江蘇中廣核某風場[21]。齒輪箱F1的壽命為威布爾分布,其形狀參數τ和尺度參數ζ分別為2.3和310,因此平均設計壽命為15a。高速軸F2的壽命為指數分布,因此故障率ω=4。其余參數可假設為:c1=3,c2=5,c3=3,c4=12,c5=7;t1=48,t2=72,t3=96,t4=192;x=0.35,y=1.1,RL=0.9。 計算結果如表1所示。由表1和圖1可知,串聯系統的維修次數N隨維修方式的改變而變化。當N<5時,串聯系統的維修費用率C隨維修次數的增大而減小;當N=5時方程達到最小值,維修費用率為48.63元,此時串聯系統最滿意的計劃型預防維修周期間隔為T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h;當N>5時,維修費用率隨維修次數的增大而增大。因此,當N=5時,可對風電機組相關部件進行預防性更換。當N=8、T8=543 h時,計劃型預防維修周期間隔接近風場常規的計劃檢修周期,如果再繼續增大N,系統停機過于頻繁,會增大維修成本,因此為了不增加額外成本開銷,不再增大N。 表1 C模型計算結果 圖1 C模型優化結果 2.2.1 模型建立 建立系統可用度最大的計劃型預防維修模型如下: (7) (8) 該模型適用于同時考慮可用度最大化和確保串聯系統工作時可靠度下界正常的情況。 2.2.2 分析求解 利用Matlab進行數值模擬,得到表2結果。由表2和圖2可知,當N<4時,系統可用度A隨N的增大而增大;當N=4時,A達到最大值0.869,此時串聯系統最滿意的計劃型預防維修周期為T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h。即當N=4后便可對系統進行相應部件的更換,這樣可確保串聯系統的可用度最大。相比C模型,A模型的N減小,但對部件的更換頻率增加,因此采用A模型雖然可以保證系統處于較高的可用度,但是多次更換部件將增加維修成本。 表2 A模型計算結果 圖2 A模型優化結果 為協調維修費用率和可用度之間的矛盾,建立一個以維修費用率最小、可用度最大為目標的可調節模型。 2.3.1 模型建立 綜合考慮維修費用率最小、可用度最大的多目標方程為: U(N,Ti)=C(N,Ti)-A(N,Ti) (9) 統一量綱并引入權重系數ρ1和ρ2: (10) 通過調節ρ1和ρ2的大小可以反映出不同可靠性指標的權重,ρ1+ρ2=1。 可調節的多目標預防維修模型為: (11) 該模型同時考慮了計劃型預防維修中的維修費用率和可用度,稱之為U模型。 2.3.2 分析求解 當ρ1=0.5、ρ2=0.5時,Matlab計算結果如表3所示。由表3可知,當N<4時,模型計算結果隨維修周期的增大而減小;當N=4時,達到最小值0.190,此時對應的風電機組齒輪箱的最滿意預防維修周期為T1=2 317 h、T2=1 813 h、T3=1 391 h、T4=1 062 h,繼續增加N,計算結果增大。 表3 U模型計算結果 ρ1=0.6、ρ2=0.4,ρ1=0.5、ρ2=0.5和ρ1=0.4、ρ2=0.6這3種情況下U隨N的變化情況如圖3所示。由圖3可知,即使模型選取不同的權重系數,當N=4時,U(N,Ti)的計算結果都取得最小值。即在第4次計劃型預防維修周期結束后對串聯系統中的相應部件進行更換,不僅維修費用率小,同時還能保證系統可用度較高。 圖3 不同權重下U模型的優化結果 將不同模型的最優解進行對比,結果見表4。 表4 不同模型計算結果的對比 由圖4不同模型的優化結果可知: (12) 圖4 不同模型的優化結果 機會型維修是指維修系統中的某一部件時,同時維修或更換短時間內需要維修的其他部件。該方式將減少系統的預防維修總次數,從而縮短系統停機時間,達到降低機組維修成本的目的[22-23]。 以維修費用率最小為目標函數,建立機會型預防維修模型(OC模型);以可用度最大為目標函數,建立可用度最大的模型(OA模型);以維修費用率最小、可用度最大為雙目標,建立可調節模型(OU模型)。將上述3種模型的計算結果與風電機組計劃型預防維修模型的計算結果進行對比。 3.1.1 模型建立 齒輪箱壽命l的分布函數為F(X),密度函數為f(X),高速軸壽命分布函數為G(X),密度函數為g(X)。M時刻高速軸的壽命分布函數表示為: (13) 密度函數為: (14) 平均維修費用率為: (15) 式中:c0為對齒輪箱進行一次機會維修消耗的費用;L1為串聯系統在第1個預防維修周期內進行機會型維修的閾值;M為當齒輪箱的壽命超過L時,高速軸第一次出現故障的時刻。 對平均維修費用率的期望函數進行求導,分析其在(0,T1)區間內是否存在最小值點,該最小值點即最優機會維修閾值L*。 (16) 已知單周期平均維修費用的期望E[C(L)]在區間上是連續函數,因此當-c0+c2+c3+c4>0時,期望函數的導數可取得最小值。將導數方程的根代入進行比較,可以得到最優機會維修閾值L*,即為OC模型。 3.1.2 分析求解 由前文計算結果可知,風電機組齒輪箱最滿意的計劃型預防維修周期間隔為T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h。 各計劃型預防維修周期內的最優機會維修閾值見表5。 表5 OC模型各計劃型預防維修周期內的最優機會維修閾值 第一個計劃型預防維修周期T1內其他參數計算結果見表6。 表6 OC模型計算結果 由表6可知,風電機組齒輪箱在T1=2 146 h內的L*是1 155 h,換言之,對齒輪箱進行機會維修的最佳時間是運行1 155~2 146 h,此時維修時間雖然相較于原計劃提前了,但是系統的維修費用率減少了22.74%。這與Sulabh的模擬結果一致。 3.2.1 模型建立 系統可用度為: (17) 平均維修費用率在區間(0,T1)2個端點處的導數為: (18) 3.2.2 分析求解 基于可用度最大時的最滿意計劃型預防維修周期來確定最優機會預防維修策略。 由第2.2節的計算結果可知,風電機組齒輪箱最滿意的預防維修周期間隔為T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h。通過計算可獲得各計劃型預防維修周期內的L*,如表7所示。 表7 OA模型各計劃型預防維修周期內的最優機會維修閾值 第一個計劃型預防維修周期T1內其他參數計算結果見表8。 表8 OA模型計算結果 由表8可知,風電機組齒輪箱在T1=2 499 h內的L*是1 388 h,即對齒輪箱進行機會維修的最佳時間是運行1 387~ 2 498 h之間,此時維修雖然在時間上相較于原計劃提前了,但是系統的維修費用率減小了6.09%,符合Sulabh的模擬結果。 3.3.1 模型建立 基于前文計算構造一個新的混合目標函數: U(LU)=E[C(LU)]-E[A(LU)] (19) 統一量綱并引入權重系數ρ1、ρ2: (20) 該模型即為OU模型。 3.3.2 模型求解 由上文計算結果可知,風電機組齒輪箱在ρ1=0.5、ρ2=0.5,ρ1=0.6、ρ2=0.4和ρ1=0.4、ρ2=0.6這3種情況下最滿意的T1分別是2 317 h、2 288 h和2 393 h。通過計算可得L*,如表9所示。 表9 OU模型最優機會維修閾值 選取不同權重系數ρ1、ρ2,得到不同權重系數下U模型的計算結果,如表10所示。 表10 OU模型計算結果 由表10可知,通過調整ρ1、ρ2的大小,風電機組齒輪箱在第1個計劃型預防維修周期內,在表10所示的機會維修閾值時,對齒輪箱進行機會維修,均可使目標函數維修費用率減小,可用度增大。可見,風電機組在維修過程中可多考慮OU模型的機會型預防維修。 無論ρ1、ρ2的數值如何變動,始終滿足如下關系式: (21) 這表明風電機組串聯系統的計劃維修中,如果著重于減小維修費用率,綜合模型更接近OC模型;如果追求系統可用度大時,綜合模型更接近OA模型。 (1)在風電機組串聯系統的計劃型預防維修模型的研究中,以串聯系統的維修費用率最小為目標函數,得出最滿意的計劃型預防維修周期間隔為T1=2 146 h、T2=1 776 h、T3=1 387 h、T4=1 103 h、T5=895 h;以系統的可用度最大為目標函數,得出系統最滿意的計劃型預防維修周期為T1=2 499 h、T2=1 857 h、T3=1 399 h、T4=1 033 h;綜合考慮兩方面因素構建了多目標的計劃型預防維修模型,如果維修費用率方面分配的權重更大,則綜合模型更接近基于維修費用率最小模型,如果可用度方面分配權重更大,則綜合模型更接近基于可用度最大模型。 (2)與計劃型預防維修模型的計算結果進行比較,發現采用機會型維修決策后,系統在單周期內的維修費用率節省了22.74%,可用度提高了6.10%。因此,機會型維修決策可以進一步減小單周期內系統的維修費用率,并提高系統可用度。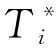
2.2 A模型

2.3 U模型
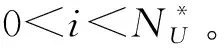
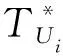
3 機會型預防維修模型
3.1 OC模型
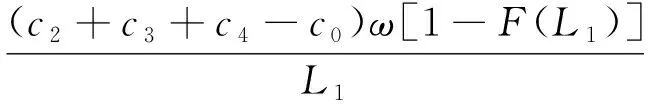


3.2 OA模型
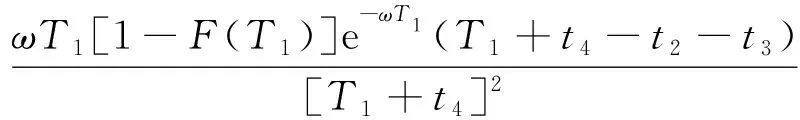
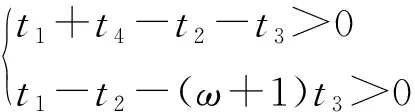



3.3 OU模型


4 結 論

