面向小型產品裝配系統的決策支持系統

丁祥海，田吉蓮

（杭州電子科技大學 管理學院，浙江 杭州 310018）

一、引言

裝配作為增值鏈中最后的分支必須能夠在經濟可行的方案的基礎上滿足市場變化的需求量。針對大規模定制批量化與定制化的生產組織要求，文獻[1]建立了以重構成本最小為目標函數的動態單元裝配系統重構的規劃模型。針對生產過程中的訂單不確定等因素，文獻[2]建立了一個魯棒調度模型，并提出了對模型進行求解的混合優化算法。針對面向資源的工程訂貨生產方式下柔性裝配生產系統的設備配置問題，文獻[3]建立了具有雙重約束的優化模型。朱劍剛[4]在面向裝配的設計基礎上對虛擬裝配技術進行系統的研究，開發了基于AutoCAD環境的定制家具虛擬裝配系統（VASCF）。此外，高度自動化的裝配系統在這個背景下，特別是在低投入和短安裝時間的人員密集型裝配中的表現并不理想。手工裝配系統因其具有較高的柔性和較低的投入的特點，更加適用于此種類型的裝配。

大批量產品的裝配基本采用完全自動的，可以選擇的范圍很窄。對于中小批量的小型產品的裝配，有許多可供選擇的手工裝配系統。但系統的多樣性并沒有在很多企業中得到應用。主要原因是決策者在尋找最佳裝配系統上會耗費太多的時間和精力。決策者傾向于現存的裝配系統。因此，如何敏捷高效地針對特定目標，選擇合適的裝配系統，是企業急需解決的難題。

二、裝配時間估算的研究背景

準確地估算裝配時間是選擇合適的裝配系統的基礎，是在大規模定制和變動的生產環境中取得競爭優勢的關鍵。所以對于裝配時間的確定國內外有很多相關的研究。

國內，劉濱等人[5]提出了產品相似實例檢索規則和算法。該算法應用神經網絡獲取實例產品的工時規律，并按此預測當前產品的裝配作業工時。最后開發了船舶裝配作業工時智能估算系統（IMHEAS）。楊青海等人[6]提出零件工時估算的相似性機理與過程模型。并在此基礎上，提出一種基于案例推理和事物特性表的零件工時估算方法。魯香珍等人[7]研究了柔性參數水平對產品族加工時間的影響機理，構建了產品族各工時模塊加工時間模型，以柔性參數水平的匹配搜索算法實現定制產品加工時間的估算。陳友玲等人[8]應用粗糙集的方法對企業現有產品的配置進行分析，定義了一個時間系數，并用回歸分析的方法建立起該系數與裝配時間的數學關系模型。此模型可通過新產品的時間系數對其裝配時間進行估算。

國外，Pedro，Pérez V.等人[9]通過使用模糊進化方法改進產品設計，以預測和優化新產品的裝配時間。文獻[10-11]提出了基于系統結構的復雜度度量的系統裝配時間預測模型。Miller，Michael.等人[12]考慮到車輛的組裝取決于產品的信息和描述過程的信息。提出將安裝流程步驟說明作為自動化裝配時間的估算工具。Miller,Michael G.等人[13]根據組件的結構復雜性創建了基于神經網絡的裝配時間預測模型。Erohin，O.等人[14]利用數據挖掘技術來預測產品的裝配時間。Namouz，Essam Z.等人[15]將兩種不同的圖形生成方法（干涉檢測方法和裝配配對方法）用于復雜連通性方法的輸入，以估計產品的裝配時間。

以上文獻都是從產品的角度進行考慮，而沒有考慮到裝配系統之間的聯系。德國弗勞恩霍夫研究所根據裝配系統的特征，并基于近似計算的方法，實現快速確定各裝配系統的裝配時間[16]。本文參考該研究所的近似計算的思想，建立了各時間組件的計算模型，并通過編程實現了基于Web的決策支持系統的開發。

三、介紹

（一）八種手工裝配系統

本文涉及的裝配系統主要是表1所示的八大基礎裝配系統，同時對這八種裝配系統的特征信息進行了簡略的描述。

（二）時間組件

單工位的裝配時間（以單工位為基準），因為軟件的目標，不是確定輸入非常精確或詳細的信息，而是快速估算所需的裝配時間作為經濟效率計算的基礎，以便選擇最佳的裝配系統。所以，使用各時間組件的標準工時來進行粗略計算。

為了以盡可能少的時間和精力為每個特定的裝配任務快速獲得所有裝配系統的裝配時間。文獻[17]在“簡化的裝配時間計算”模型中做出了一組假設，實現了只需少量的必要的數據即可計算裝配時間。它根據一個員工在單工位中裝配一個產品的假定的裝配時間作為參照，其值即為每件產品的預設時間。其他裝配系統的裝配時間根據與參照系統的時間組件的差異來間接獲得。時間組件模型如表2所示，時間組件分為積極的（-）和消極的（+）。根據相應的裝配系統，列中標有“+”的時間組件將被添加，例如，手工U型生產線需要傳輸單個半成品到下一工位，這個時間就需要加上；標有“-”的時間組件需要減去，例如，轉位工作臺對一個工件載體上的待裝配對象只用抓取一次物料，對照單工位節省的時間就需要減去。

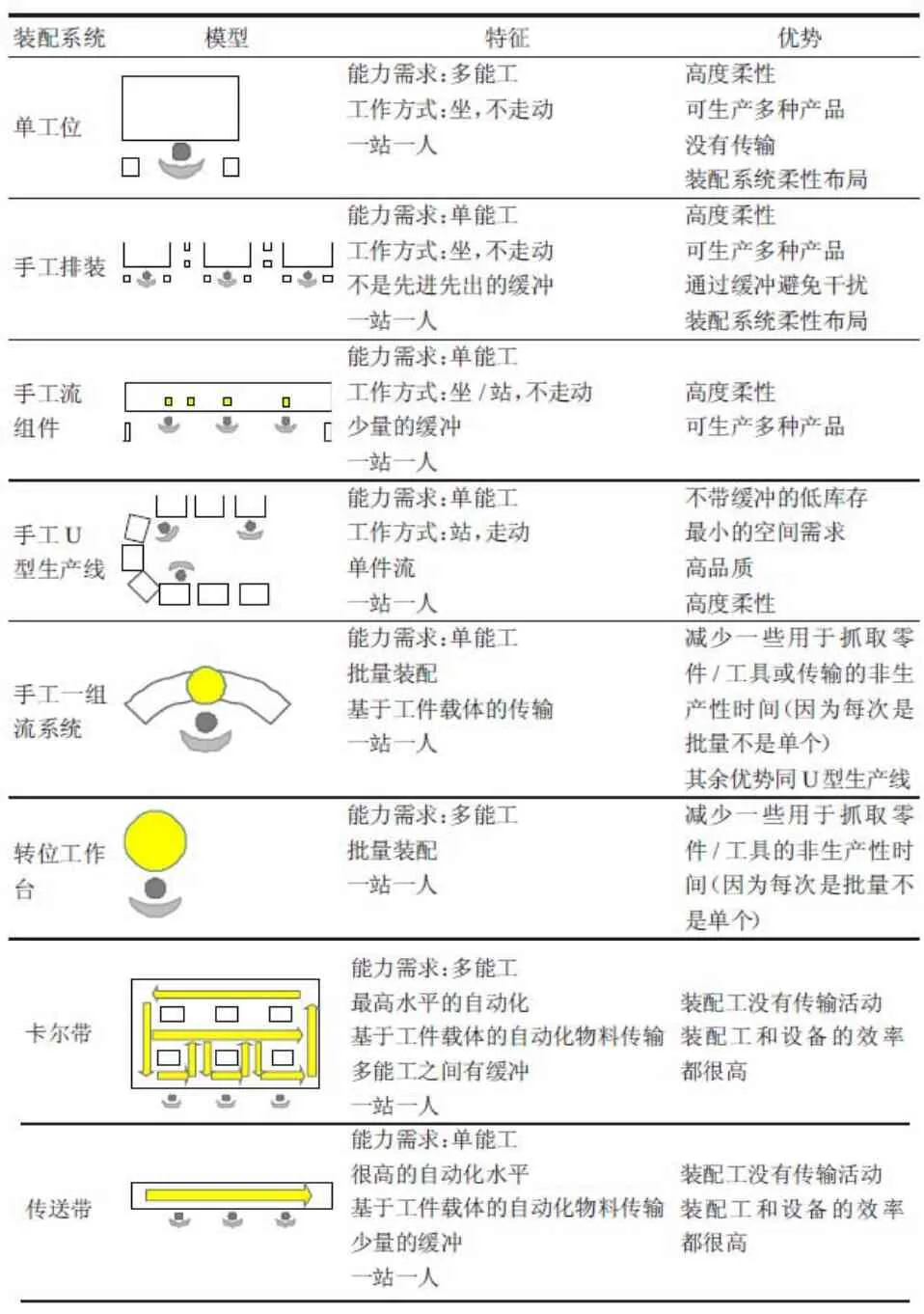
表1 八種裝配系統特征信息表

表2 計算裝配時間的時間組件模型

四、決策支持系統的設計

由于企業以盈利為目的。因此，本文對各裝配系統的決策目標是時間成本和經濟效率，其中經濟效率由設備成本和工資成本組成。針對上述目標，本文的重點是建立各裝配系統的時間組件計算模型，以下就對各模型進行論述。

（一）模型假設

裝配系統的選擇是個復雜的過程，考慮過多的因素會使模型的建立難度加大。而合理的模型假設可以抓住主要因素拋開次要的因素，既能很好地簡化模型又能得到需要的結果，從而準確反映決策的本質問題。具體假設如下：（1）工位數與人員需求量相等，即一站一人；（2）產品可由其中一種裝配系統裝配完成；（3）時間均為標準工時（工位的安排一定，各種物料工具的所放位置確定）；（4）采用固定聯結；（5）設備和人員都能滿足生產能力需求；（6）不考慮廢品率（沒有廢品，都是合格品）；（7）只加工一樣產品，即不用進行作業排序；（8）工位之間均進行翻轉，則在單工位上裝配一件產品的翻轉次數為（工位數-1）次；（9）裝配一件產品只抓取一次工具；（10）裝配一件產品需拿取物料的次數與工位數相等。

（二）符號體系

模特法相較于其他PTS法有2點優勢：（1）模特法將動作歸納為21種，不像其他方法有幾十種，甚至100多種；（2）采用模特法不需要測時，也不用進行評比，就能根據其動作決定正常時間。因此，使用它來分析動作和制定標準時間。

1.標記。對系統決策過程中涉及的員工需求量、1MOD的時間、模特法的動作記錄方式和寬放率進行標記，具體如下：m為員工需求量；mod為1MOD的時間，mod=0.1431秒；模特法的動作記錄方式如：M3G1表示伸手抓取；k為寬放率，k=0.17。

2.輸入參數。對決策過程中涉及時間成本計算的相關參數進行標記，包括產品日需量、系統使用度、每件產品的預設時間、員工每日出席時間、員工每日自由時間、員工負載率、工件載體容量和緩沖容器容量，具體如下：n為產品應以n件/天的速度生產；Sn為系統使用度；Te為每件產品的預設時間；Ta為員工每日出席時間；Tp為員工每日自由時間；Lg為員工負載率；p為工件載體容量；b為緩沖容器容量。

3.決策變量。裝配系統的決策變量為：各裝配系統在相應的時間組件的裝配時間，用Ti表示，其中i=1，2，…，7。各裝配系統的裝配時間表示具體如下：Tsj為單工位的裝配時間；Tram為手工排裝的裝配時間；Tfam為手工流組件的裝配時間；Topm為手工U型生產線的裝配時間；Tosm為手工一組流系統的裝配時間；Tit為轉位工作臺的裝配時間；Tca為卡爾帶的裝配時間；Tco為傳送帶的裝配時間。

（三）數學模型

通過以上假設、輸入參數和決策變量的設定，建立了如下數學模型：

式（1）為手工流組件傳輸單個半成品到下一工位的時間，也表示手工排裝將半成品取出和放入緩沖容器的時間；式（2）為手工U型生產線傳輸單個半成品到下一工位的時間；式（3）為手工排裝傳輸緩沖容器到下一工位的時間；式（4）為手工U型生產線的員工從最后一個工位回到第一個工位的時間；式（5）為手工排裝、手工流組件、手工U型生產線、卡爾帶和傳送帶這幾個裝配系統由于不用在傳輸過程中翻轉產品而節省的時間；式（6）為手工一組流系統和轉位工作臺由于對一個工件載體上的待裝配對象只需抓取一次工具而節省的時間；式（7）為手工一組流系統和轉位工作臺由于對一個工件載體上的待裝配對象只需抓取一次物料而節省的時間。表3給出了八種基礎裝配系統的裝配時間模型。

表3 八種裝配系統的裝配時間模型

五、系統開發與演示

該系統操作流程圖如圖1所示，系統軟件環境客戶端選擇了Windows 10操作系統，用IntelliJ IDEA 2017.3.5x64為開發平臺，以mysql-connectorjava-5.1.36為后臺數據庫管理系統。

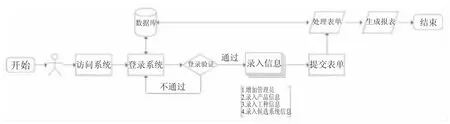
圖1 系統操作流程圖

（一）數據庫完整設計圖

圖2為該系統的數據庫設計圖，主要由四張表構成。

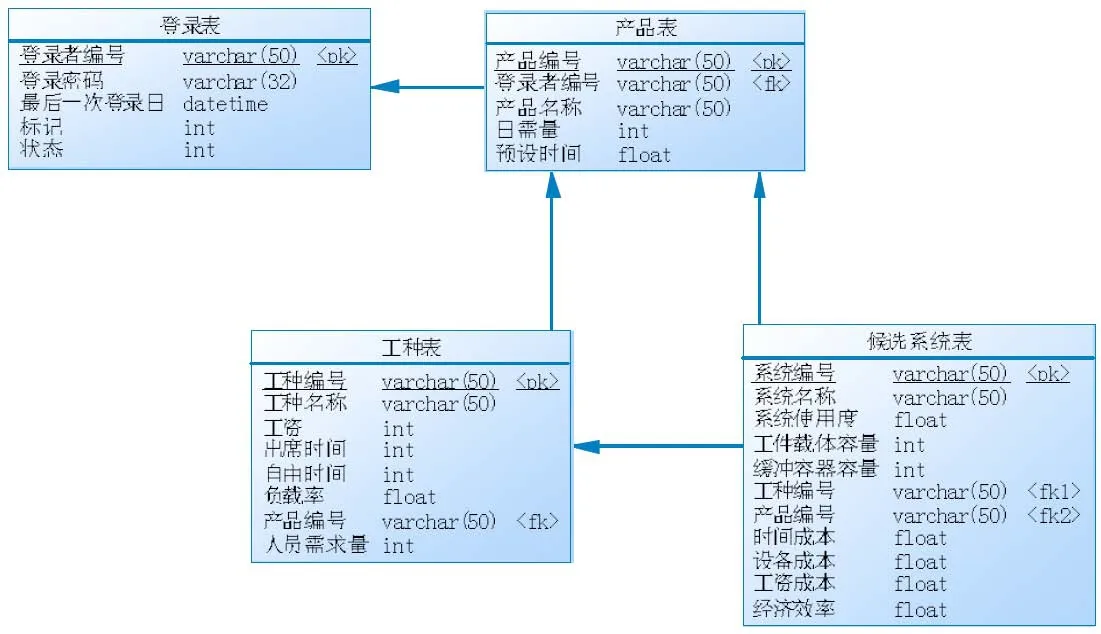
圖2 數據庫完整設計圖

（二）演示

現以生產筆記本電腦為例，有以下信息如表4和表5所示。

表4 輸入信息

根據這些信息生成的報表如圖3所示，可以看出針對該目標產品，八種裝配系統的時間成本差別不大，但經濟效率差別明顯。決策者可以根據實際情況，選擇合適的裝配系統。

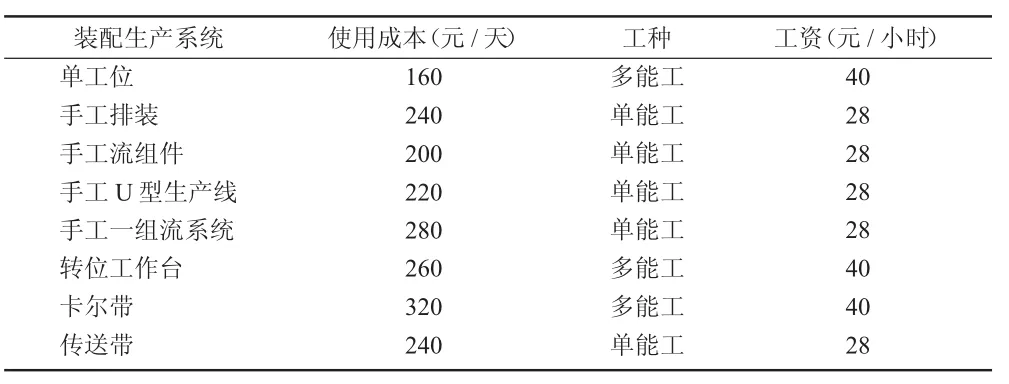
表5 數據庫信息

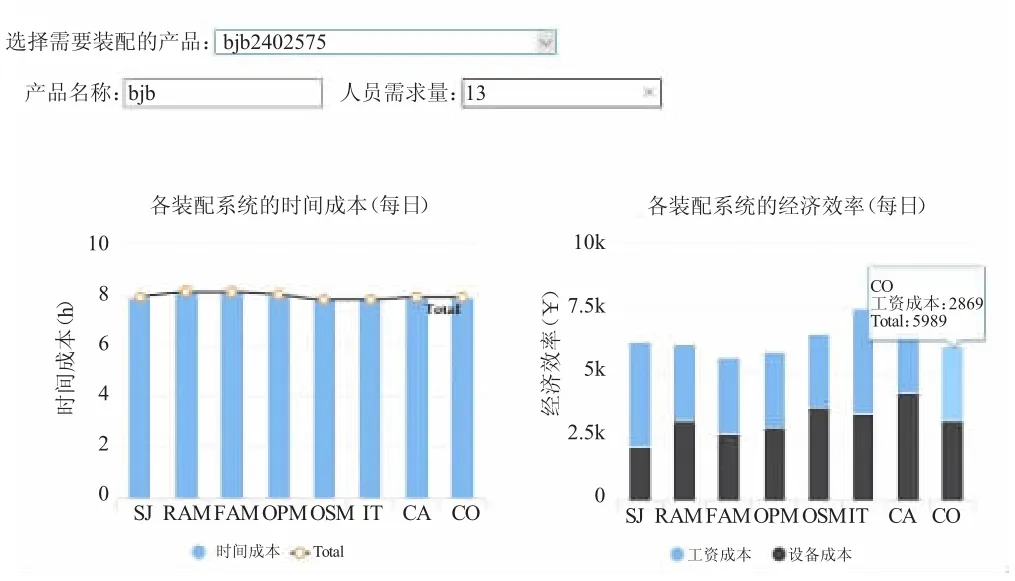
圖3 報表管理界面

六、結語

企業面臨著越來越大的價格壓力，產品生命周期的縮短，每種產品數量的減少和銷量的難以預測。生產環境的這些變化增強了智慧規劃和選擇合適的裝配系統的重要性。小型產品的手工裝配系統的多樣性提供了足夠的范圍來尋找經濟的解決方案。通過本文的決策支持系統，能夠輕松地比較各裝配系統。即使用戶對裝配系統只了解一點點也能使用該系統。其可以幫助決策者在早期規劃階段選擇合適的裝配系統，來應對快速變化的產品需求量，并確保選擇的裝配系統是有效的。本文的假設前提是產品可由一種裝配系統裝配完成，在后續的研究中，將對八種裝配系統進行組合，并快速生成更加滿足決策者需求的候選裝配方案。此外，本文在決策目標中沒有考慮面積成本，在接下來的研究中需要將決策目標進行完善。