多元表征，讓數學學習深度發生——以“乘法分配律”為例

江蘇省常熟市塔前小學 顧培華

【問題描述】

《乘法分配律》是蘇教版四年級下冊探索運算規律的內容之一。每每教完這一內容，發現總有一部分學生陷于與乘法分配律的對錯糾纏，對乘法分配律的本質內涵與外在形式的對接時而清晰，時而模糊。老師就不得不再次強調乘法分配律的意義、特征、注意點等，再不然就通過大量的題海訓練來解決問題。可事實上，用這樣的方式沒法讓學生徹底擺脫與乘法分配律的尷尬相遇。

【內涵解讀】

多元表征學習是基于學生認知規律，組織引導學生進行數學深度學習的學習方式，其本質內涵是將數學學習對象進行心理多元認知編碼并與之建立對應、建構意義聯系，是建構“內化—聯系—外化”的數學深度學習生態循環系統。因此，多元表征學習是學習數學的一種重要策略。

【創新設計】

一、設計初心

教師：教學過程要遵循學生的認知規律，為學生創設與教材文本深度對話的多元表征方式，外顯知識的形成過程，溝通知識的內在聯系，讓學生通過多種不同的表征感悟統一的數學模型。

學生：學習過程中要學會選擇和跟進合適的表征方式，經歷知識的“個性化”過程，從而對嚴密抽象的數學知識注入自己的密碼，留下自己的痕跡，能夠在自主表征的過程中講述自己的數學故事。

二、設計策略

1．多元表征學習設法激活、喚醒已知，找準深度學習的邏輯起點

學習即聯系，關乎學生已有的個體經驗，這里的經驗包括孩子積累的生活經驗和學習經驗。在學習過程中，教師可以通過創設情境等方式，給學生一個自主攝取原有相關經驗的有效通道，實現對新知學習所需經驗的激活與喚醒，為獲取新知提供思考的基礎和支撐，進而讓學生進行自主解釋和表征，敞亮知識生成發展的邏輯。

（1）鏈接已有經驗中乘法分配律的“原點”

基于乘法分配律算式表征的本質內涵是含有相同的幾個幾，那選擇怎樣的情境表征能夠有效引領孩子深度學習呢？

蘇教版教材之所以從原先的“求校服總價”改編成現在的“求跳繩總數”，究其原因是為了便于學生調取原有經驗中最適切的“生長種子”。

原校服問題：（60+40）×3=60×3+40×3

3個60加40的和=3個60加3個40

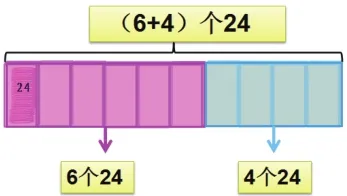
現跳繩問題：（6+4）×24=6×24+4×24

6+4即10,10個24=6個24加4個24

引導學生結合已有經驗，可以用言語表征和算式表征解決問題的方法。

方法一：先求四、五年級一共有多少個班？（6+4）×24；

方法二：先分別求出四、五年級各領多少根跳繩？6×24+4×24。

（2）鏈接已學知識中乘法分配律的“原型”

等學生自主探究出乘法分配規律后，及時引導學生回顧已學知識中這種規律的存在“身影”，讓學生經歷剝離乘法分配律存在的不同“外衣”，進一步去理解其本質內涵。

鏈接1：口算、筆算方法的角度

出示：12×3=36，引導學生可以看作（10+2）個3。

方法一：口算 方法二：筆算

即：（10+2）×3=10×3+2×3。

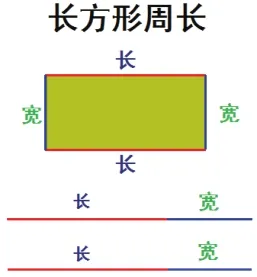
鏈接2——長方形周長的角度

出示：長方形有2條長、2條寬。

即：長×2+寬×2=（長+寬）×2。

2．多元表征學習引發探究、建構模型，夯實深度學習的多元外化

學習即建模，關乎孩子當下的自主狀態。學生在數學課堂上是亦步亦趨地依葫蘆畫瓢，還是積極探究后的自主建構，答案無可厚非，但過程卻值得為師者用心探索。在數學學習的過程中，讓孩子們通過自主操作、觀察比較、互動交流后自主表征出個體對知識的理解樣態，然后在集體交流中進一步辨析糾偏、厘清本質、歸納完善，從而真正為數學學習建構屬于自己的數學理解。

（1）根據“含有幾個幾”列出等式

課堂上，首先根據給出的實際問題引導學生畫圖表征出解題過程，明確兩種方法結果相等的本質含義和內在聯系——都含有10個24。

（2）緊扣“含有幾個幾”進行圖式互換表征。

①圖的表征→式的表征：根據動態圖形表征寫出得到的等式。

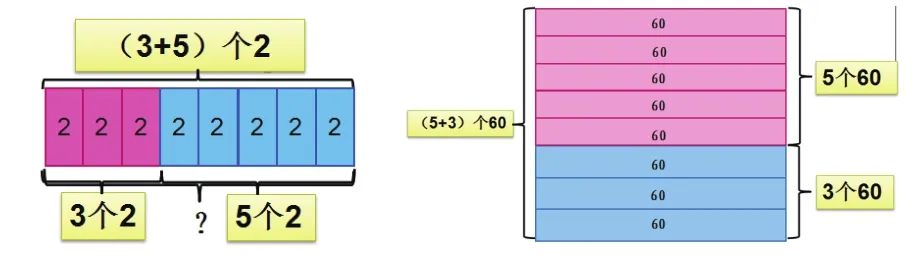
（3+5）×2 = 3×2+5×2 （5+3）×60 = 5×60+3×60

②式的表征→圖的表征：根據等式用圖形進行表征。（4+2）×10=4×10+2×10

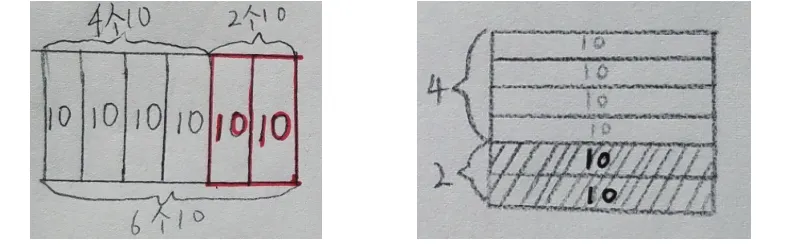
（3）經歷“觀察比較、猜想驗證”的探究過程

將學習過程中得到的幾個等式作為后續研究的學習素材：

（6+4）×24 = 6×24+4×24

（3+5）×2 = 3×2+5×2

（5+3）×60 = 5×60+3×60

（4+2）×10 = 4×10+2×10

通過觀察等式，比較異同——引發猜想，舉例驗證——抽象本質，總結規律的深入學習，引導學生用言語表征出這個規律的內涵，并鼓勵學生自主用符號表征出發現的規律，用一個等式表示出來：

在交流內化的基礎上表示出乘法分配律：（a+b）×c=a×c+b×c。

3．多元表征學習溝通關聯、激勵想象，達成深度學習的思維拓展

（1）溝通關聯

①抽取面積模型解釋乘法分配律

對原來圖式進行轉換轉譯，鋪上對應小長方形。通過計算大長方形面積，發現和原來求幾個幾的題目表面上看完全不同，但實質是完全相通的。

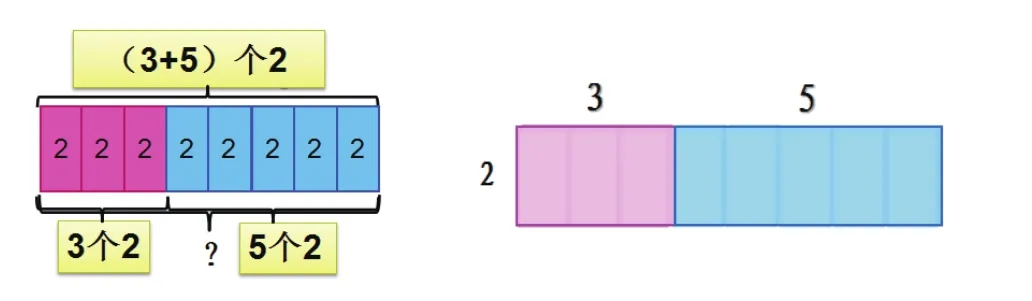
大長方形面積=兩個小長方形面積之和

（3+5）×2=3×2+5×2

②幾個幾的另一種解釋及兩種方法的溝通

從（60+40）×3=60×3+40×3這個等式，既能看出（60+40）個3=60個3+40個3，等式兩邊都表示有100個3。還可以換個角度看到不同的幾個幾（見下圖）：

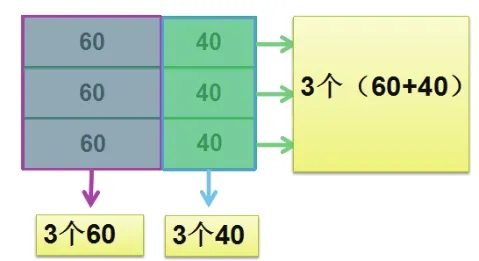
從圖形表征來分析，橫看是3個（60+40），豎看是3個60與3個40的和。不管看到幾個幾，都可以用乘法分配律來解釋。

（2）拓展想象

課末，將“兩個數的和”拓展到“兩個數的差”，將“兩個數的和”拓展到“三個數的和”，進而引發孩子展開新一輪的自主猜想、舉例驗證……在獨立的個性解讀與表征過程中，進一步豐富對乘法分配律的認識。

現在孩童在數學課堂上的想象與創造就是將來數學學習中的嚴密推理和發現的前身，故此讓我們堅定地堅持吧！

【后續思考】

將多元表征滲透到數學課堂教學中，一方面可以調動學生多感官的認知因素，促進知識的理解，培養學生的數學思維以及促進學生數學智慧的生長；另一方面，通過對問題進行多元化的表征，為學生解決數學問題提供了新的平臺，從而有助于提高學生對問題多角度的解釋能力和創新能力。數學中多元表征的教學策略為：深度對話文本，找準深度學習的邏輯起點；運用教育機智，夯實深度學習的多元外化；引導關聯想象，達成深度學習的思維拓展。讓我們正確運用并發揮多元表征的“正能量”，讓學生在數學課堂上的深度學習真正發生。