基于標簽傳播的重疊社區發現算法

吳 春 國， 李 艷 振， 李 瑛， 高 瑞， 時 小 虎*

(1.吉林大學 符號計算與知識工程教育部重點實驗室， 吉林 長春 130012；2.吉林大學 計算機科學與技術學院， 吉林 長春 130012；3.吉林大學珠海學院 計算機學院， 廣東 珠海 519041 )

0 引 言

現實世界中的許多問題都可以簡化為復雜網絡進行研究.因此，越來越多的研究者熱衷于研究復雜網絡，挖掘其隱藏價值.復雜網絡擁有很多特性，如小世界性(small world)[1]、無標度性(scale-free)[2]和高聚集特性等.此外，復雜網絡還呈現出明顯的社區結構[3-4].社區結構也可稱作網絡簇結構.在社區結構中，同一個社區內邊數很多，節點之間連接稠密，而跨社區相連的邊相對比較稀疏.那些具有相似功能或屬性的節點組成相同的社區，而不同的社區相互連接構成完整的復雜網絡.相對于整個系統，社區就像人體結構中的一個器官或者組織，為了更好地解釋和了解復雜系統功能，需要對社區的結構進行分析和研究.自從Girvan等[3]提出了社區發現的概念以來，復雜網絡社區發現的研究成果不斷涌現，主要可以分為譜方法、模塊度優化方法、層次聚類方法和邊預測方法等[5].

在實際生活中，復雜網絡中的節點可以同時存在于多個社區中，因此這些社區之間會有重疊部分.在社交網絡中，每個個體通常具有多個不同的社區屬性，可能同時屬于多個社會團體，如家庭、朋友圈、同事圈.同樣，社區重疊現象廣泛存在于生物分子網絡中.比如在基因調控網絡或者蛋白質相互作用網絡中，單個基因或者蛋白質往往參與多個生物功能表達過程.因此，研究復雜網絡的重疊社區或者重疊節點具有非常重要的意義.又比如在網絡謠言的傳播中，那些處于重疊節點位置的個體對于謠言的擴散傳播起了決定性的作用.研究重疊節點的性質有助于深入理解謠言的傳播機制.在生物網絡中，不同的生物功能之間相互關聯，并非完全割裂，重疊節點往往預示著關鍵信息，對于人類疾病的治療、農作物抗病性的研究都具有重要意義.

近年來，重疊社區發現算法研究取得了很大進展，典型的算法大致可以分為5類[6]：派系過濾算法、邊劃分算法、局部擴展與優化算法、模糊發現算法、標簽傳播算法.Palla等于2005年提出了派系過濾算法的代表方法——CPM(clique percolation method)[7]，其基本思想是復雜網絡中多個派系(完全子圖)之間相互重疊，構成了復雜網絡中的社區.派系過濾算法通過尋找相互連通k-派系的方法確定社區結構.派系過濾算法也可以實現重疊節點的社區發現，因為在派系過濾算法中的單個節點可能屬于不同k-派系.邊劃分算法將復雜網絡中的邊進行劃分，從而對復雜網絡中的社區結構進行挖掘.如果一個節點連接在一條邊上，而且這條邊被劃分到多個邊聚簇中，則此節點被判定為重疊節點[8-9].局部擴展與優化算法的社區發現過程是利用局部擴展與優化算法完成的.在社區發現的過程中，這種算法使用局部社區或者已發現社區組成種子社區，而節點之間連接的緊密程度往往通過局部密度函數進行度量[10-11].模糊發現算法在每一個節點上計算歸屬因子向量(belonging factor)[12]，以此來計算社區與社區的聯系強度和節點對的聯系強度.標簽傳播算法的主要思想是用標簽傳播的方式來確定每一個節點所屬的社區，這是比較流行的一類算法.Gregory等在非重疊節點社區發現的標簽傳播算法LPA基礎上將每個節點的標簽用多個類標簽標識，并引入隸屬度的概念，提出了COPRA算法進行重疊節點社區發現[13-14].SLPA算法也是一種標簽傳播的重疊社區發現算法，它通過模擬演講者-收聽者來完成標簽傳播過程[15].在LPA算法中，復雜網絡中的節點不會記住在某一時刻接收到的標簽信息.與之不同的是，SLPA算法會保存節點曾經收到的所有標簽，為每一個節點設立一個用于存儲對應標簽概率分布的存儲區，其中的存儲概率分布表示了當前節點的歸屬強度.文獻[16]介紹了一種完全不一樣的標簽傳播算法SpeakEasy.該算法運行速度快，適合不同種類的網絡，但存在的問題是在識別重疊節點過程中可能出現重疊節點比重過大的現象.

本文借鑒SpeakEasy算法的思想，首先通過標簽傳播算法得到初始的無重疊社區劃分，然后通過設計新的節點識別算法確定重疊節點，最后再對社區進行合并，提出OCPLP(overlapping community partitioning based on label propagation)算法.通過在LFR人工數據集、3個標準公開測試集以及真實的大豆基因共表達網絡上對本文提出的算法與已有算法進行對比.

1 SpeakEasy算法簡介

SpeakEasy與COPRA、SLPA等算法一樣，都是以標簽傳播為基礎，通過標簽傳播把每個節點劃分到對應的社區中.不同的是，SpeakEasy同時考慮整個網絡的全局標簽分布情況與局部標簽分布情況，結合了自頂而下策略與自底而上策略對標簽進行傳播.自頂而下策略主要是依據當前復雜網絡中的全局標簽分布情況來決定標簽的傳播，自底而上策略則主要考慮當前節點與鄰居節點組成的局部子圖中的標簽分布信息.

SpeakEasy算法可以分為兩個階段：第1個階段是非重疊社區劃分，首先進行標簽傳播過程，待標簽傳播收斂以后，可以提取到一個完整的非重疊社區劃分結果，重復此過程Nt次，得到Nt個非重疊劃分，從Nt個劃分中篩選出一個最優劃分.如果不考慮重疊節點的話，此時已經得到了社區劃分的結果.第2個階段是重疊節點識別，即在最優劃分基礎上識別重疊節點.首先根據得到的Nt個劃分結果計算共生矩陣A，A中的元素aij表示節點vi和vj在Nt次劃分中被聚為同一個社區的次數.如果最優劃分某個社區C之外的某個節點v與C中的節點的共生次數大于給定閾值，則可以認定v為C的重疊節點.定義節點v和社區C的平均權值為

(1)

當Wv C大于給定閾值γ時，認定v為C的重疊節點.

SpeakEasy算法的優勢在于較少人工設定參數，適合不同種類的網絡圖，快速完成擁有大量節點的網絡圖的處理任務.不足之處是此算法在識別重疊節點時會有重疊節點比重過大的現象.

2 OCPLP算法

SpeakEasy算法存在兩個問題.首先，當網絡圖規模較大且圖中重疊節點較多時，兩個社區之間會有大量的重合區域.其次，小社區對大社區內的節點吸引力過大，會存在“蛇吞象”現象.為了解決這兩個問題，本文分別設計了新的重疊社區發現算法，并在最后增加了社區合并過程，提出了OCPLP算法，具體如下：

(1)隨機初始化網絡圖

設整個網絡圖G包含n個節點，以每個節點的ID作為社區的標簽信息.首先為每個節點i建立大小為Nb的緩沖區，記為bi，用以保存最近Nb次更新的標簽.初始化時從該節點的鄰居節點中隨機抽取Nb次，將選中的鄰居節點ID填入緩沖區，如圖1所示.

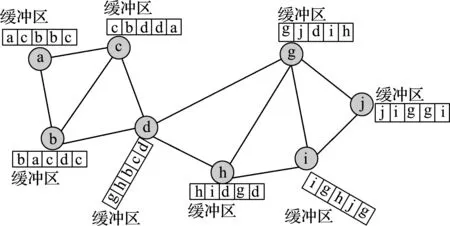
圖1 隨機初始化網絡圖

(2)標簽傳播

①計算標簽的全局概率分布，即計算所有標簽在圖G中全部節點緩沖區中的概率分布：

(2)

其中ni為第i個標簽在圖G中所有節點緩沖區出現的次數總和.

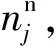
(3)

③計算每個節點的標簽局部特異性，即該節點的鄰居節點緩沖區中標簽的實際分布與期望分布之差.記第i個標簽在第j個節點的局部特異性為sji，則其計算公式為

(4)

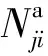
④更新節點的緩沖區.對于第j個節點的緩沖區bj，選擇最大的sji所對應的標簽作為該節點的新增標簽，即刪除bj中的第1個元素，在隊尾插入所選擇的標簽.

⑤重復②～④，遍歷圖G中所有節點.

⑥重復①～⑤，直到所有節點的緩沖區收斂.

例如在圖1中一共有8個標簽a、b、c、d、g、h、i、j，其全局概率分布依次為3/40、5/40、6/40、7/40、7/40、4/40、5/40、3/40.以節點d為例，其鄰居節點的緩沖區的標簽a、b、c、d、g、h、i、j的實際數量分布為2、2、3、6、2、2、2、1，總數為20.而按照全局概率分布，這8個標簽的期望數分別為1.5、2.5、3.0、3.5、3.5、2.0、2.5、1.5.因此8個標簽的特異程度分別為0.5、-0.5、0、2.5、-1.5、0、-0.5、-0.5，最大的為標簽d的2.5.因此對節點d的緩沖區進行更新時首先刪除其第1個位置的d，其余4個位置的c、b、h、g分別前移1位，末尾補充特異性最大的標簽d.

(3)抽取社區劃分結果

根據上述得到的標簽分布結果進行社區劃分，具體過程如下：

①統計第j個節點所有鄰居緩沖區中的標簽數.將數目最多的標簽作為該節點的所屬社區ID.該社區若已經存在，則將第j個節點劃分到此社區中；若不存在，則以該ID新建社區，并添加第j個節點為該社區元素.

②重復①，遍歷圖中所有節點，假設共建立了k個社區，也就是說得到了一個包含k個社區的劃分結果P={C1，C2，…，Ck}.

(4)選擇最優劃分

(5)

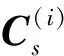
(6)

選擇最大評價一致性的劃分為最優劃分.如果不考慮重疊節點的話，該劃分就是最終社區劃分的結果.

(5)識別重疊社區節點

計算Nt個劃分的共生矩陣A，元素aij表示節點vi和vj在Nt次劃分中被聚為同一個社區的次數.定義節點v和社區Ci的平均權值為

(7)

若Wv Ci>γ1，則節點v為社區Ci的重疊節點，γ1為設定的閾值.需要指出的是，式(7)中不僅考慮了社區Ci的規模，而且也考慮了社區Cj的規模，這樣就在很大程度上避免了將大量大類節點計入小類的重疊節點，從而導致重疊節點比例過大的問題.識別重疊社區節點算法的偽代碼如下：

OCPLP-識別重疊社區節點

： 重疊節點的閾值γ1，共生矩陣A

： 最優劃分C，圖中全部節點集合G

1： function FindOverlapNodes(γ1，A，G，C)

2： forv∈Gdo

3： forci∈Cdo

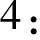
5： ifWv Ci>γ1then

6：Ci←Ci∪{v}

7： end if

8： end for

9： end for

10： end function

(6)社區合并

如果兩個社區之間重合部分占比達到設定閾值，則合并這兩個社區，即

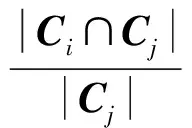
其中γ2為設定的閾值.算法偽代碼描述如下：

OCPLP-社區合并算法

： 合并社區的閾值γ2，共生矩陣A

： 最優劃分C，圖中全部節點集合G

1： function MergeCommunities(γ2，A，C，G)

2： forCi∈Cdo

3： forCj∈CandCj≠Cido

4： if |Ci∩Cj|/|Cj|>γ2then

5： forv∈Cjdo //合并Cj到Ci

ifv?Cithen

Ci←Ci∪{v}

6： end if

7： end for

8： deleteCj

9： end if

10： end for

11： end for

12： end function

3 實 驗

為驗證本文算法的有效性，共設計了3個實驗.首先利用LFR benchmark算法[17]生成虛擬的重疊網絡，在人工數據集上將本文提出的OCPLP 與SLPA[15]、SpeakEasy[16]兩種當前主流重疊社區劃分算法進行對比.在第2個實驗中選擇幾種常用的公開標準測試集，比較OCPLP與兩種比較算法的性能.最后一個實驗選擇了實際的大豆基因共表達網絡，分別使用SpeakEasy和OCPLP算法對基因共表達網絡進行重疊社區劃分，并且比較兩種算法的結果.

3.1 LFR benchmark數據集對比

LFR benchmark引入網絡度分布和社區大小分布的指數等參數來生成重疊網絡，所生成的網絡能夠模擬現實網絡中的重要性質[17].LFR benchmark中提供了多種參數以控制生成網絡的拓撲結構.本文利用LFR benchmark工具生成了3個人工網絡圖：LFR1、LFR2、LFR3.表1列出了生成3個網絡圖時所使用的參數，各個參數的定義如下：N為節點數，m為邊數，k為平均度，kmax為最大度，μ為混合程度，non為重疊節點數，noc為每個重疊節點從屬的社區個數.

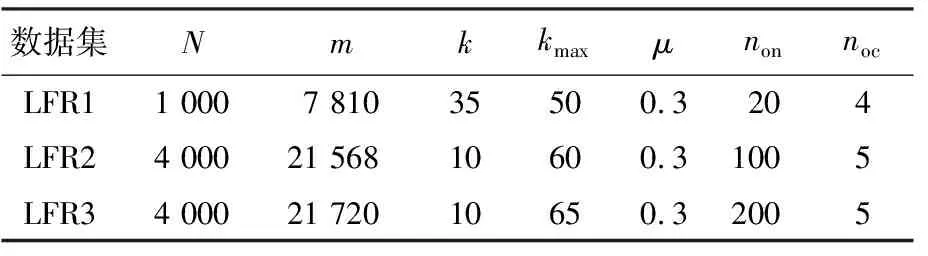
表1 生成LFR benchmark網絡圖的參數

復雜網絡重疊社區發現算法的性能常用模塊度Q[18]作為評價指標，其定義如下：

(8)

式中：m為網絡中總的邊數；Oi表示節點i所屬社區個數；Nij=1代表節點i和節點j之間存在連邊，否則不存在連邊；ki為節點i度數；li為節點i屬于某個社區的標號；δ(li，lj)=1當且僅當li=lj.

評價復雜網絡重疊社區發現算法的性能的另一個常用指標為標準化互信息，對兩個劃分P(i)和P(j)，其標準化互信息為[11]

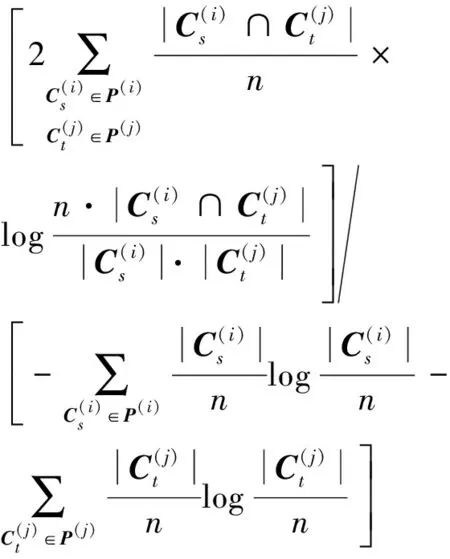
(9)

OCPLP與兩種比較算法的模塊度Q和標準化互信息In的對比結果如表2所示.緩沖區大小對結果整體影響不大，在本文實驗中該參數取值為5.從表2可以看出，在人工數據集的兩個指標上，OCPLP算法比SLPA、SpeakEasy兩種算法表現略好.

表2 LFR benchmark數據集上的對比結果

下面重點考察對重疊節點的識別情況，將識別重疊節點的過程理解為二分類問題，將重疊節點理解為正樣本，將非重疊節點理解為負樣本，用召回率γr、精確率γp、F1度量3個評估指標來評價OCPLP算法與兩種比較算法的優劣.

γr=nT/(nT+nN)

(10)

γp=nT/(nT+nP)

(11)

F1=2×(γr×γp)/(γr+γp)

(12)

其中nT為真陽性樣本數，即對正類樣本預測正確的樣本數；nP為假陽性樣本數，即把負類樣本預測為正類的樣本數；nN為假陰性樣本數，即把正類樣本預測為負類的樣本數.

表3給出了在LFR1、LFR2、LFR3人工數據集上重疊節點識別的比較結果.由表3可以看出，在LFR1上，3種算法在3個指標的綜合表現差異不大，其中OCPLP的表現最好.在LFR2和LFR3上，3種算法的表現差異明顯，其中SLPA表現最差，而OCPLP的表現明顯優于其他兩種比較算法.在LFR1、LFR2、LFR3人工數據集上的平均精確率，OCPLP分別比SLPA和SpeakEasy 提高了83%和42%，而平均召回率則分別提高了55%和22%，F1度量分別提高了84%和40%.可以看出，OCPLP算法在這3個指標上全面優于SpeakEasy算法，而SpeakEasy算法又明顯強于SLPA算法.

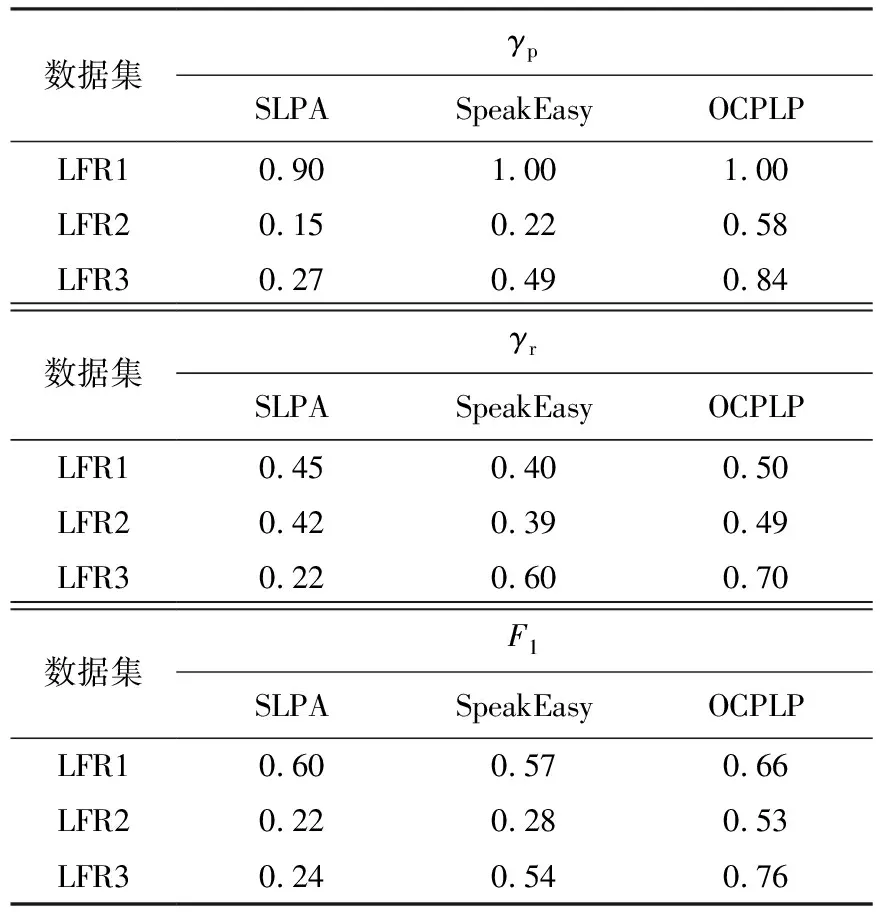
表3 重疊節點識別的對比結果

3.2 公開標準測試集對比

本文選擇pol.books[19]、arxiv廣義相對論學者合作網絡(general relativity and quantum cosmology collaboration network)[20]和netscience[19]3個較為流行的公開數據集進行對比實驗.

pol.books是基于亞馬遜網站的美國政治類型書籍購買信息而構造的網絡，有105個節點，441條邊；arxiv廣義相對論學者合作網絡包括5 242 個節點和28 980條邊；netscience是復雜網絡學者合作網絡，由1 461個節點和2 742條邊構成.在3.1節的實驗中可以看出SpeakEasy算法明顯優于SLPA算法，所以在后面的實驗部分只選擇SpeakEasy算法與OCPLP算法進行對比.

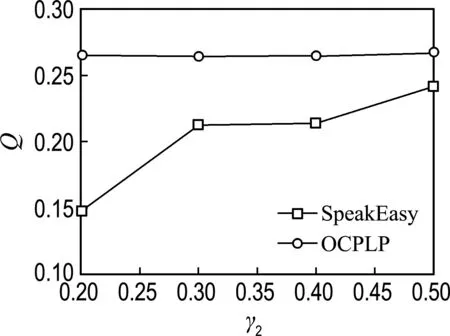
(a) pol.books

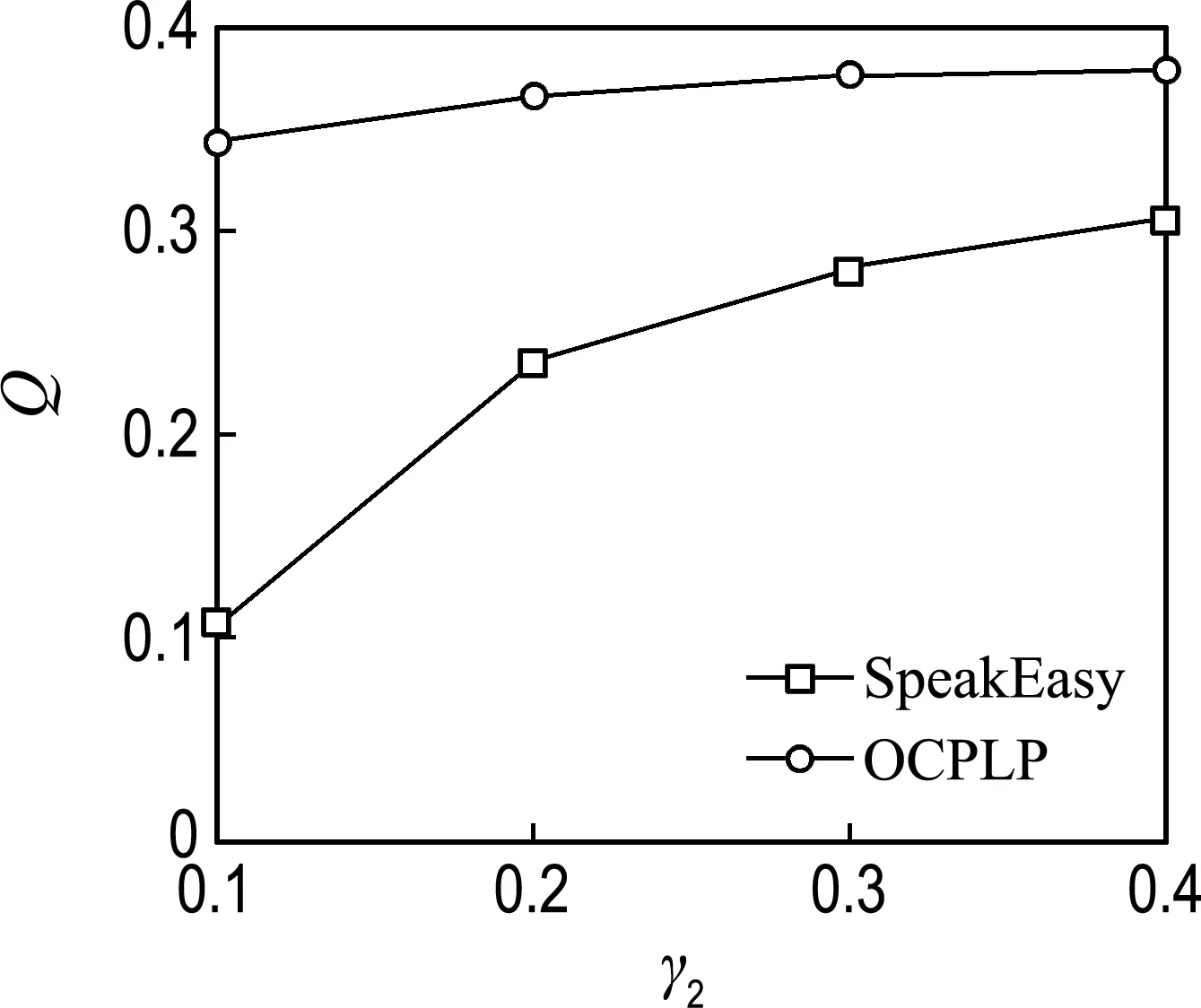
(b) arxiv廣義相對論學者合作網絡

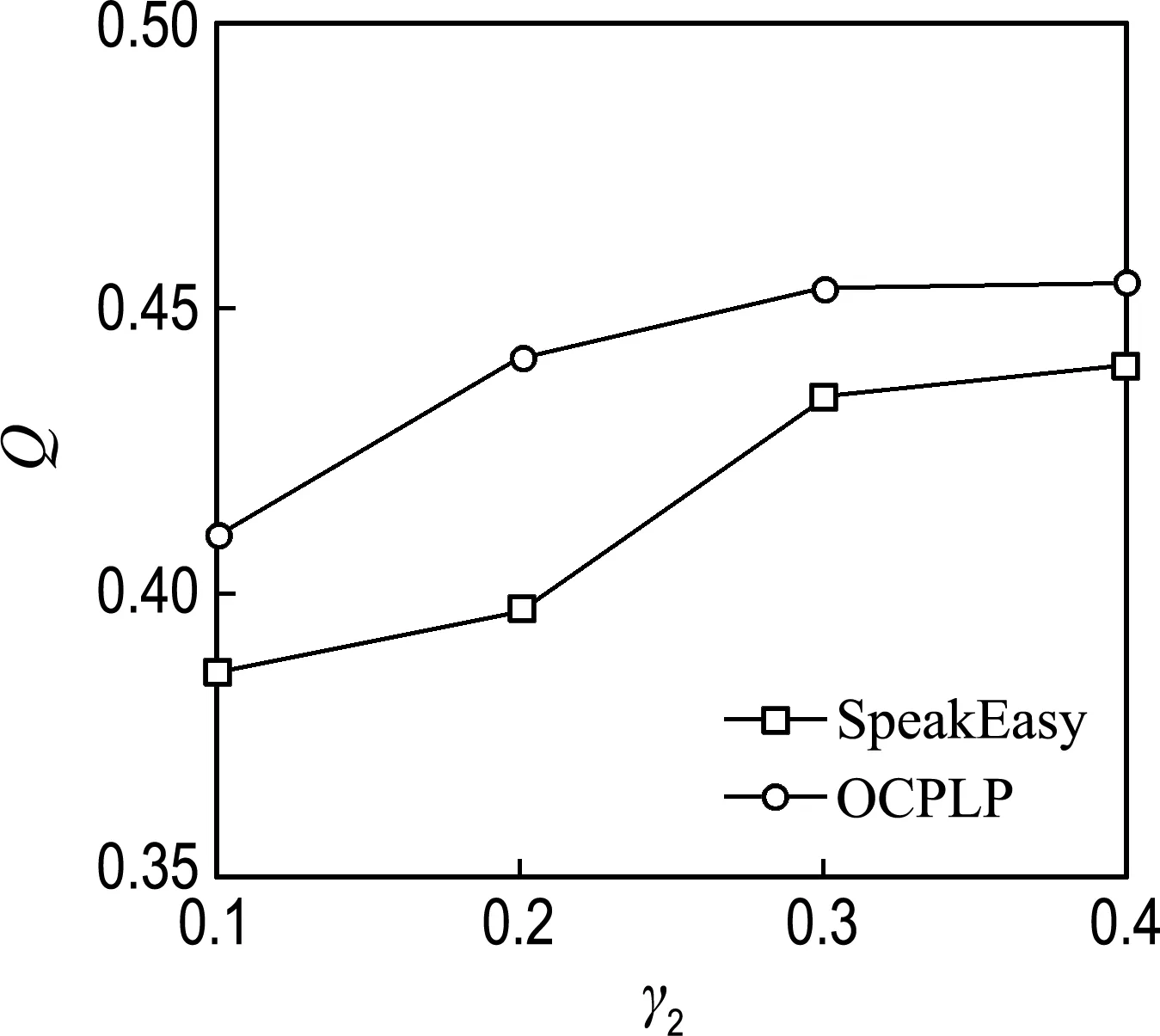
(c) netscience

圖2 典型網絡數據集的對比結果

Fig.2 Comparison results on the classical network datasets

圖2給出了OCPLP算法和SpeakEasy算法在3個數據集上的對比結果.從圖中可以看出，在3個真實數據集上OCPLP算法在不同閾值下的模塊度Q都明顯高于SpeakEasy算法.其中，在pol.books數據集上平均提高了34.53%，在arxiv廣義相對論學者合作網絡上平均提高了84.16%，而在netscience網絡上平均提高了6.30%.

3.3 大豆基因共表達網絡對比實驗

為了進一步驗證所提算法的有效性，本文利用大豆基因共表達網絡構造了社區發現算法的測試算例.實驗數據源于GEO數據庫GPL4592平臺下的6組大豆銹病相關的數據(GSE7108[21]、GSE8432[22]、GSE29740[23]、GSE29741、GSE33410[24]、GSE41724).通過計算基因之間的皮爾森相關系數構建了一個大豆基因共表達網絡.該網絡包含4 169個基因，21 135條邊，每兩個基因之間的相似度作為對應邊的權重，平均度為10，平均聚類系數為0.56.針對所構建的大豆基因共表達網絡，分別采用SpeakEasy算法和OCPLP算法對該網絡進行社區劃分.

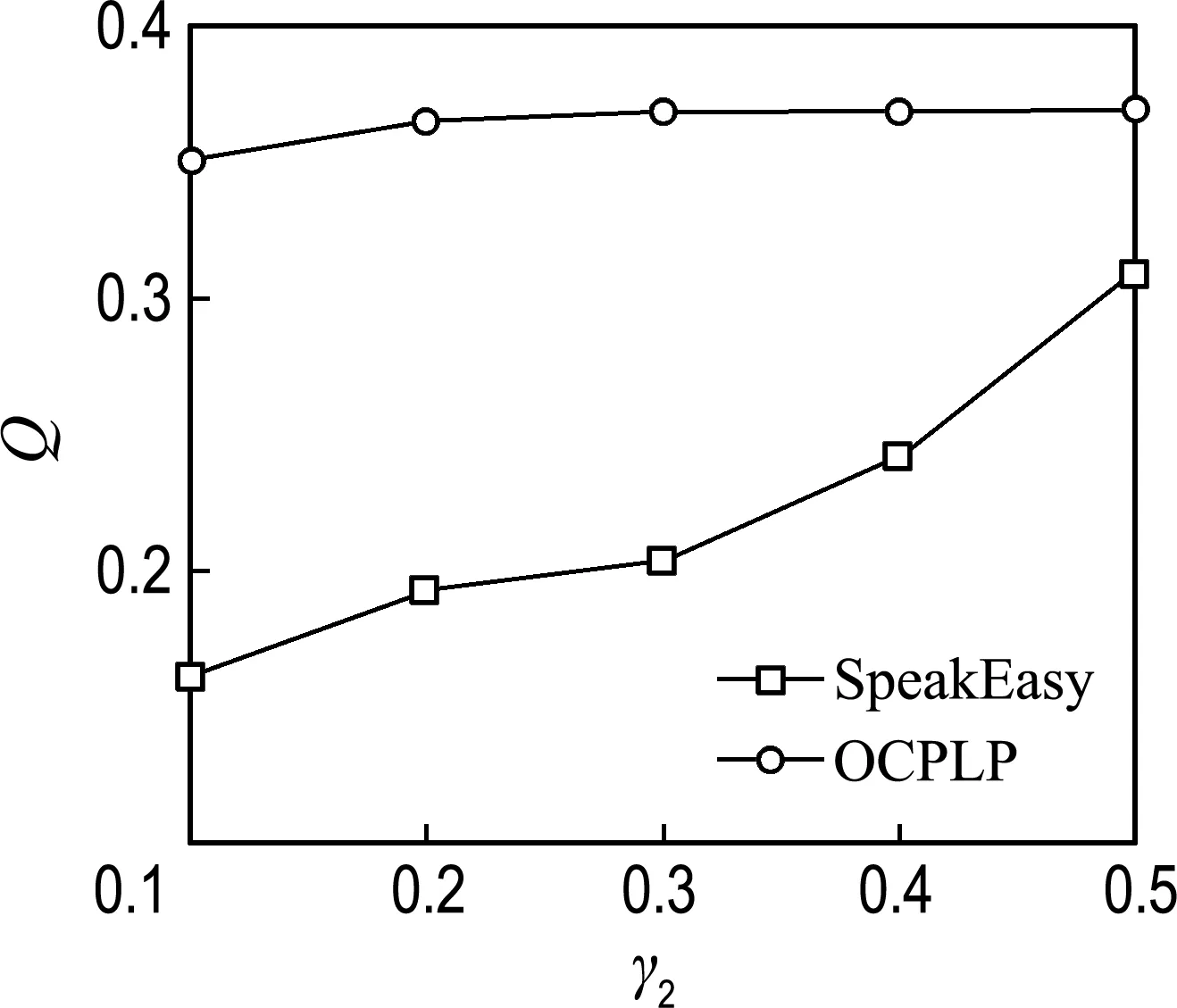
圖3 大豆基因共表達網絡對比結果

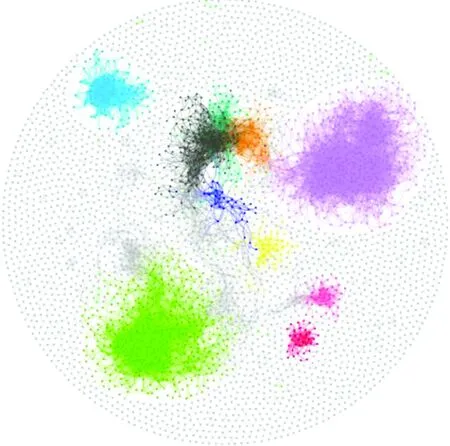
圖4 大豆基因共表達網絡實驗可視化效果

從圖3可以看出，OCPLP算法在不同閾值下得到的模塊度Q都較高，社區劃分結果更好.圖4給出了OCPLP算法對大豆基因共表達網絡進行社區劃分的可視化效果.對社區劃分結果做進一步分析有助于研究在銹病環境下大豆的基因共表達現象，并為大豆育種提供幫助.

4 結 語

針對重疊節點社區發現問題，本文通過設計新的重疊社區發現算法，增加社區合并過程，提出了OCPLP算法.為驗證所提算法的有效性，分別針對LFR benchmark人工數據集、3個典型標準數據集以及實際的大豆基因共表達網絡設計了3個實驗，將本文提出的算法與現有算法進行了對比.實驗結果表明，本文提出的OCPLP算法性能明顯優于對比算法，并極大改善了重疊節點比重過大的問題，使得結果更加符合問題的實際特征，也驗證了OCPLP算法的有效性.