C/C復合材料微觀尺度燒蝕過程質量損失速率模擬*

宋永善，齊樂華，張守陽，張佳平，李逸仙，李賀軍

(1.西北工業大學 機電學院，西安 710072；2.西北工業大學 C/C復合材料研究中心，西安 710072)

0 引言

C/C復合材料具有一系列優異的性能[1-3]，如高強度、高模量，以及其強度隨溫度升高不降反升，此外還具有良好的抗熱沖擊、抗燒蝕、熱膨脹系數低及良好的導熱性能，是迄今為止惰性氣氛下最為理想的高溫結構材料之一，被廣泛用于固體火箭發動機喉襯、飛行器頭錐等航空航天結構部件。然而，在高溫、高速沖擊等極端苛刻的服役環境下，C/C復合材料不可避免地會發生燒蝕現象，進而導致材料性能急劇下降。

目前，關于C/C復合材料的燒蝕問題已經開展了很多實驗研究，但受燒蝕過程中的高溫限制，實驗研究所能測量的參數只有線燒蝕率和質量燒蝕率，燒蝕機理的研究也大多基于對燒蝕后材料表面的微觀形貌進行分析，得到的信息十分有限。數值模擬因此成為進一步深入研究C/C復合材料燒蝕機理不可或缺的手段。Piyush Thakre等[4]和Daniele Bianchi等[5]基于不同假設分別計算了C/C復合材料發動機噴管的熱化學燒蝕過程。王臣等[6]通過對碳基復合材料熱化學燒蝕機理分析，根據質量守恒、能量守恒及系統化學反應的熱化學平衡原理，建立了相應的熱化學和熱力學燒蝕模型，模擬了材料內部熱應力場分布。楊德軍等[7]采用虛擬失效、重新構建網格部件的方法實現燒蝕表面的退縮，建立了燒蝕表面退縮下瞬態溫度場的有限元模型，分析了熱化學燒蝕、燒蝕表面退縮及溫度場耦合作用下 C/C復合材料燒蝕性能的變化規律。解惠貞等[8]研究表明，纖維分布方向對C/C復合材料的燒蝕性能有重要影響，垂直燃氣流方向的纖維與平行燃氣流方向的纖維的線燒蝕率和質量燒蝕率區別非常大。汪海斌等[9]針對軸編C/C復合材料的結構形式和燒蝕機理，建立了噴管喉襯燒蝕的多尺度分析方法。通過宏觀-微觀的漸進分析，獲得了噴管喉襯的燒蝕率和燒蝕形貌。王臣[10]建立了C/C復合材料的表面氧化模型來研究材料的燒蝕過程和熱環境參數，并與實驗結果吻合良好。上述研究主要針對C/C復合材料的宏觀燒蝕機理分析，未考慮C/C復合材料中炭纖維和碳基體在密度和性能上的差異，因而很難揭示微尺度下C/C復合材料燒蝕過程中的形貌變化。實際上，C/C復合材料微尺度下的形貌變化會導致其宏觀尺度的表面粗糙化，進而加劇材料表面的傳熱、傳質，影響材料表面的流場。Lachaud J等[11]通過理論計算結合實驗測定了C/C復合材料及其組分(纖維、基體)的固有氧化速率，建立了穩態下C/C復合材料氧化模型，推導出的函數能直接計算氧化達到穩態時纖維的形貌，但未能給出燒蝕過程中的微觀形貌演變規律。

本文建立微觀尺度燒蝕過程的形貌演變瞬態模型，研究C/C復合材料微觀燒蝕過程中纖維和基體的相對質量損失規律，以期為研究C/C復合材料微觀燒蝕機理提供借鑒。

1 燒蝕過程建模

1.1 基本假設

在承受高溫高速沖刷的苛刻服役環境中，C/C復合材料會因氧化、升華、等離子腐蝕和機械剝離而被逐漸破壞，導致不能忽略的表面退移，該現象被稱為燒蝕。同時，燒蝕還會產生其他作用[5]：(1)增大反應表面，進一步加劇發生在材料表面的傳熱和傳質；(2)表面粗糙化導致C/C復合材料的有效燒蝕速率不能簡單地用其組分的燒蝕速率算術平均代替；(3)加劇機械剝離；(4)導致層流向湍流轉變。

但材料燒蝕率較低，對氣體流動的連續性影響較小，故本文對燒蝕模擬過程做了簡化，做出如下假設：(1)氣源位于離初始材料表面足夠遠的一個距離；氣體流動狀態為層流；(2)氧化反應為一階反應。則材料表面的氧化速率可定義為

v=-kCVmol

(1)

式中v為材料的氧化速率，m/s；k為氣體反應速率常數，m/s；C為局部反應氣體濃度，mol/m3；Vmol為材料的摩爾體積，m3/mol。

1.2 水平集法

本文采用水平集法來追蹤燒蝕過程中材料的表面移動。材料表面由水平集函數定義：

(2)

其中，d為到材料表面的最短距離，φ=0代表材料表面。在定義了φ的初值及合適的速度場v后，可以通過計算水平集方程(3)來的追蹤材料的表面移動。

(3)

但燒蝕速度v只在材料表面有物理意義，針對這種情況，必須通過外推構造合適的速度場。本文選用方程(4)所示方法[12]進行外推：

(4)

式中φ為速度v的任意一個分量。

方程(4)中符號函數S(φ)和單位法向量n分別定義為

(5)

(6)

在計算方程(3)一個步長后，φ不再為符號距離函數，必須重新初始化。通過求解方程(7)直至穩態可以完成重新初始化。

(7)

方程(7)中sign(φ0)被定義為

(8)

式中τ為虛時間；φ0為求解水平集方程(3)一個步長以后得到的水平集函數。

1.3 擴散方程

氣體區域和氣-固界面分別采用擴散方程(9)和(10)描述氧化過程中反應氣體的質量傳輸：

(9)

-DCn=-kf/mC

(10)

式中D為反應氣體的擴散系數；kf/m為由材料組分決定的非均相反應速率常數。

根據邊界條件(7),可得

v?DCnvmol

(11)

將式(11)等號右側的r向z向分量分別代入方程(4)外推，可得到外推后的速度場vext。

氧化過程中，材料表面不斷移動，這意味著每計算一個步長，都要重新設定邊界條件。為了避免這種情況，本文選擇文獻[13]中的近似方法。對邊界條件(10)作如下處理。

氧化過程中，反應氣體在材料表面處的消耗SC可表示為

(12)

函數δ(φ)表示為

(13)

其中，ε為正比于網格大小的參數。函數δ(φ)的特點為在區間[0,2ε]內的積分1,且在φ=ε處取最大值。

經過處理后的邊界條件(12)可整合為方程中的源項：

(14)

擴散系數被定義為φ的函數：

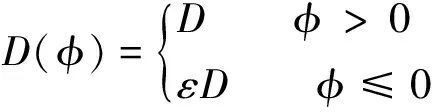
(15)

氣體中擴散系數為D，為了避免材料表面附件的數值震蕩，材料一側氣體擴散系數被定義為一個非常小的數εD。

1.4 計算方法

在COMSOL中建立如圖1(a)所示的2D軸對稱模型。如圖1(b)所示，模型中纖維半徑為r，基體厚度為t，材料初始長度為h1，氣源距材料表面的初始距離為h2。模型通過映射方式劃分正方形網格，網格尺寸為10-5mm，氣源處邊界條件為給定的初始濃度。

求解C/C復合材料燒蝕形貌的具體計算流程圖如圖2所示。模擬中通過Comsol中的系數型PDE模塊寫入擴散方程(14)，定義相應的初始值和邊界條件。其中，C和φ均通過COMSOL with MATLAB以插值函數形式分別導出和導入COMSOL。

(a)模型基本框架 (b)局部網格

圖2 C/C復合材料燒蝕過程計算流程Fig.2 Flow digram of computation for C/C composites during ablation

不同時刻的相對質量Δm的計算通過COMSOL后處理中的體積積分功能實現，具體過程如下：

(1)在COMSOL后處理模式中計算各時間步長下的纖維體積Vf。計算公式為

Vf=(1-H(φ))dVindomainr≤rf

(16)

Vm=(1-H(φ))dVindomainr>rf

(17)

式中r為2D軸對稱坐標下的橫坐標變量；rf為纖維半徑值；H(φ)為定義的Heaviside函數。

通過引入Heaviside函數可以很好地平滑界面處的不連續，得到更準確的結果。

(2)記初始時刻的纖維體積為Vf0，其余時刻的纖維體積為Vfi。則不同時刻纖維的相對質量Δmi=Vfi/Vf0，相應的基體的相對質量Δmi=Vmi/Vm0。

2 燒蝕過程相對質量損失速率分析

2.1 穩態結果驗證

本文建立了半徑為3.5 μm的單根纖維及包裹在纖維外圍的厚度為0.5 μm的界面層組成的C/C復合材料模型。燒蝕的溫度大約為3000 K，設定此時的氣體擴散系數為7×10-4m2/s[14]；此時界面層的氧化速率常數km=182 m/s[15]。圖3(a)為D=7×10-4m2/s，kf=20 m/s，km=180 m/s時計算得到的穩態形貌，纖維形狀呈不規則的圓錐形，纖維母線為曲線；圖3(b)是單向C/C復合材料氧乙炔焰后的表面形貌，燒蝕溫度2500 ℃，O2和C2H2氣體流量分別為0.24 L/s和0.10～0.20 L/s，燒蝕時間為60 s，火焰距試樣表面距離為10 mm,焰流密度為2.38 MW/m2，與圖3(a)中的仿真形貌吻合良好。

2.2 燒蝕過程相對質量損失速率

在氧化過程中，材料形狀發生了劇烈變化，增大了纖維的露出表面，增加了基體距離氣源的相對距離。為了準確分析這種變化對纖維和基體質量損失速率的影響，本文對纖維和基體微觀形貌達到穩態之前的質量損失過程進行了分析。

Jean Lchaud提出了C/C復合材料微尺度的穩態燒蝕模型[16]，模型定義了Sherwood數Sh和反應速率比A，本文以這兩個參數作為變量，計算了不同反應/擴散機制下C/C復合材料的微觀形貌演變過程。由于材料的形貌演變過程十分緩慢，只保存形貌演變過程中的特定時間的數據。特定時間的選擇基于Vignoles G L[17]提出的參考時間公式:

τ0=rf/(C0υskf)

(18)

圖4為A=5，Sh分別取0.01、0.1、1時的纖維和基體相對質量損失曲線；圖5為Sh=0.1，A分別取2、4、8時的纖維和基體相對質量損失曲線。其中，Δm為纖維當前的相對質量。圖6為A=5時反應氣體的濃度變化云圖。

(a)計算結果 (b)實驗結果

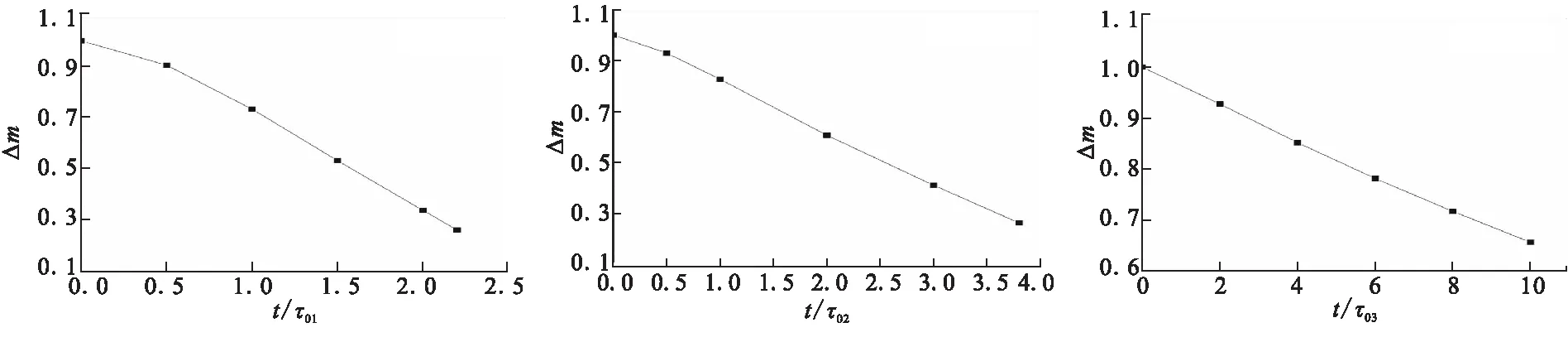
(a)A=5，Sh=0.01時,纖維 (b)A=5，Sh=0.1時,纖維 (c)A=5，Sh=1時,纖維

(d)A=5，Sh=0.01時,基體 (e)A=5，Sh=0.1時,基體 (f)A=5，Sh=1時,基體

由圖4(a)可見，當Sh=0.01，A=5時，在C/C復合材料微觀形貌演變過程中，纖維質量損失速率迅速增大，在t=τ0時達到最大值。

由圖6(a)可以發現，在整個形貌演變過程中，材料表面反應氣體濃度值基本一致，大致保持0.85C0的高濃度，這是因為反應氣體的擴散系數較高。但觀察形貌演變過程中5條濃度等值線(0.85C0～0.9C0)的變化，可以發現，最初濃度等值線完全緊貼材料表面，與纖維的輪廓相仿，露出纖維表面的濃度一致，但隨著材料形貌演變的進行，濃度等值線不再保持之前的形狀，露出纖維底部的濃度低于纖維頂部的濃度，基體表面的反應氣體濃度降低。因此，纖維質量損失速率并沒有隨著纖維露出表面的增大而持續增大，在之后受擴散的制約，纖維露出表面的增大不能加劇纖維的質量損失。

圖4(b)、(e)為當A=5，Sh=0.1時計算得到的燒蝕過程，τ02為參考時間。可以發現與圖4(a)類似的現象，在形貌演變初期(t=0～τ02),基體被大量消耗，使纖維露出表面增大，纖維質量損失速率在燒蝕初期就達到了最大值，但質量損失速率的增幅已不太明顯。隨著燒蝕的進行，由于反應氣體擴散系數較低，纖維底部與纖維頂部出現了明顯的濃度差(圖6(b))，但露出纖維表面的增大還能夠略微增大纖維的質量損失速率。但對基體來說，其質量損失速率迅速減小，保持穩定(圖4(f))。

(a)Sh=0.1,A=2時,纖維 (b)Sh=0.1,A=4時,纖維 (c)Sh=0.1,A=8時,纖維

(d)Sh=0.1,A=2時,基體 (e)Sh=0.1,A=4時,基體 (f)Sh=0.1,A=8時,基體

(a)Sh=0.01 (b)Sh=0.1 (c)Sh=1

由圖4(c)可見，當Sh=1，A=5時，纖維質量損失速率幾乎保持恒定，說明燒蝕過程為純擴散機制控制。由圖4(f)可見，當Sh=1，A=5時，基體的質量損失速率迅速減小，并很快達到穩態。

由圖6可知，當反應速率比一定時，隨著Sh的增大，擴散反應堆氧化反應的抑制逐漸增大，當Sh=0.01時，燒蝕主要受氧化反應控制；當Sh=1時，燒蝕過程則主要受擴散反應控制。

由公式(18)可知，τ06=2τ05=4τ04，則隨著反應速率比A的增大，基體質量損失基體相對于纖維的相對質量損失的變化進一步增大，且相對質量損失速率達到穩態所需的時間增加，如圖5所示。

3 結論

(1)基于水平集算法，耦合擴散方程建立了C/C復合材料在纖維尺度下的2D軸對稱燒蝕模型，計算了C/C復合材料的微觀形貌演變過程。

(2)燒蝕至穩態的模擬結果與C/C復合材料燒蝕后的微觀形貌吻合較好，驗證了本文模型的可靠性。

(3)分析了Sh數和反應速率比A對纖維和基體的相對質量損失速率的影響規律。隨著Sh的降低時纖維的相對質量損失速率會迅速增大并在燒蝕形貌達到穩態前穩定，基體的相對質量損失速率會迅速降低并在燒蝕形貌達到穩態前穩定；纖維和基體的相對質量損失速率達到穩態所需時間隨反應速率比A的增大而增大。