常應變率下某固體推進劑非線性粘彈性本構關系研究*
陳 鑫,賈有軍,郜 婕,李 偉,李錄賢
(1.西安交通大學 航天航空學院,機械結構強度與振動國家重點實驗室/陜西省先進飛行器服役環境與控制重點實驗室,西安 710049;2.中國航天科技集團四院四十一所,西安 710025)
0 引言
固體推進劑發動機具有大推力、高可靠性、方便使用維護等優點,已成為航天運載火箭的主要動力推進裝置,在世界各國航天運載技術發展中發揮著重要作用。固體推進劑是固體火箭發動機的能源材料,也是結構材料,其力學性能直接影響著整個發動機的性能。
固體推進劑力學性能的主要研究內容之一是固體推進劑的本構關系。固體推進劑在制造、貯存、使用等過程中,其力學性能受到溫度、應變率的影響[1]。目前,國內外學者已經根據各種實驗對固體推進劑的力學性能進行了廣泛深入的研究,并建立相應的本構模型,但由于固體推進劑的力學性能十分復雜,已有的相關研究與實際需求仍然存在較大差距。如Ho[2]建立了考慮損傷、溫度和應變率因素的非線性本構模型,能夠預測固體推進劑高應變率下的非線性粘彈性力學響應,但溫度較低時,預測效果不是很好。朱-王-唐本構模型[3-4]雖較好地考慮了準靜態和動態條件,被大量運用于高聚物、炸藥等脆性材料中,但只適用于變形小于20%的情況,對于高達80%以上的應變,仍需進一步完善。Schapery課題組[5-7]、孟紅磊等[8]、姚東等[9]在這方面也做了大量工作,其采用宏觀物理量的變化來描述固體推進劑變形時所表現出的非線性行為,回避了對微觀結構的復雜分析。但是,這些非線性本構模型中一般都含有多個物理意義含糊的材料參數,且所采用的是與線性本構模型基本無關的另一套體系。
固體推進劑是典型的粘彈性材料,其粘彈性行為因應變率不同而顯著不同。實驗表明,不同應變率下固體推進劑的拉伸曲線差異非常明顯。基于該實驗現象,本文從線性粘彈性本構關系出發,研究應變率對固體推進劑材料力學性能的影響,擬發展一種參數數量少、物理意義明確的固體推進劑材料的唯象非線性粘彈性本構關系,以描述固體推進劑的實驗結果,方便應用于藥柱結構的實際分析,為高裝填比固體火箭發動機裝藥結構設計提供支持。
1 線性粘彈性基本理論
單軸應力狀態下材料的線性粘彈性本構關系用積分形式可表示為
(1)
式中σ為應力;ε為應變;t為時間;E(t)為材料的松弛模量。
松弛模量E(t)可通過將式(1)應用于松弛實驗來獲得。松弛實驗是在初始時刻給定一個突變的初始應變并予以保持、然后測取應力隨時間變化的實驗。也就是說,在松弛實驗中,其應變變化為
ε(t)=ε0H(t-0)
(2)
式中H(t-t0)為Heaviside函數。
這樣,松弛實驗的應變率為
(3)
式中δ(t-t0)為Dirac delta函數。
將式(3)代入式(1),對于松弛實驗,得
(4)
一般地,松弛模量可用Prony級數表示:
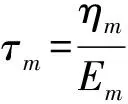
在給定環境溫度下,對于ε0=5%,松弛實驗得到的松弛模量隨時間的變化如圖2中實線所示。

圖1 廣義Maxwell模型Fig.1 Generalized Maxwell model

圖2 松弛模量的實驗值與理論計算值Fig.2 Relaxation modulus from test and theory

(6)
將式(6)中的參數值代入式(5)中,即得到松弛模量的表達式,預測的松弛模量如圖2中各點所示。可以看出,與實驗值吻合良好。
得到松弛模量后,就建立起了如式(1)的線性粘彈性本構關系。下面將該關系用于常應變率拉伸實驗。
(7)
式(7)即為依據線性粘彈性本構關系得到的常應變率時的應力隨時間變化關系。
考察應變率為0.02 s-1的情形,實驗獲得的應力-時間曲線如圖3中的實線所示,根據式(7)預測的應力-時間曲線如圖3中的虛線所示。可以看出,二者只在6%以內的小變形階段具有較好的一致性;在其余的較大應變范圍內,二者出現較大偏差。因而,需要研究非線性粘彈性本構關系,以期在更寬應變范圍或整個過程與實驗結果一致。

圖3 常應變率實驗結果與線性粘彈性理論計算結果對比Fig.3 Comparison of the results from the constant- strain-rate test and the theory
2 非線性粘彈性基本理論
2.1 推進劑材料非線性性能的影響因素
在第1節中,利用松弛實驗獲得松弛模量,進而建立了線性粘彈性本構關系。但是,如此得到的線性粘彈性本構關系對常應變率拉伸實驗預測的效果并不理想,只在小變形階段適用。隨著應變增大,線性本構關系與實驗曲線出現明顯差異,而且越來越大,說明線性粘彈性本構關系不再適用。
雖然根據式(6)的松弛模量參數獲得的常應變率應力時間關系式(7)不能很好描述實驗結果,但分析式(7)函數的基本形態是一件饒有興趣的事。直接采用式(7)對0.02 s-1的實驗結果進行擬合,得到的參數值為
(8)
式(7)表示的應力隨時間變化規律將如圖4所示。可以看出,以式(8)代替式(6)、式(7)與實驗曲線的吻合程度在整個變形過程都得到了顯著改觀。

圖4 改進預測與實驗對比Fig.4 Comparison of the results from the improved theory and the test
由此看來,在廣義Maxwell模型中采用恰當的彈性模量和粘性系數,就可很好預測常應變率實驗結果,進而獲得相應的本構關系。由于這種本構關系中材料參數是根據常應變率實驗結果擬合而得,與松弛實驗獲得的相應參數并不相同,其機理可解釋為粘彈性元件中的彈簧和粘壺性能因應變率效應發生了改變,因而,將基于常應變率實驗擬合得到的參數(如式(8))所對應的粘彈性本構關系稱為應變率相關的非線性粘彈性本構關系。
2.2 非線性粘彈性本構關系
由2.1節分析可知,應變率效應使得粘彈性元件的材料參數發生變化,引起了材料的非線性粘彈性行為。據此,仿照積分型線性粘彈性本構關系,提出積分型非線性粘彈性本構關系為
(9)
式中ER(t)為非線性松弛模量,由常應變率實驗確定。
仿照式(5),ER(t)也可表示為
(10)

為便于實際應用并保證精度,對式(10)仍取二項三參數形式,即
(11)
其物理意義可表示為如圖5所示的非線性三參量固體。
σ(t)=at+b(1-e-ct)
(12)
根據式(7),不難得到
(13)
根據式(13),可反演得到材料參數為
(14)

圖5 非線性三參量固體材料參數的物理解釋Fig.5 Physical interpretation of the three nonlinear parameters
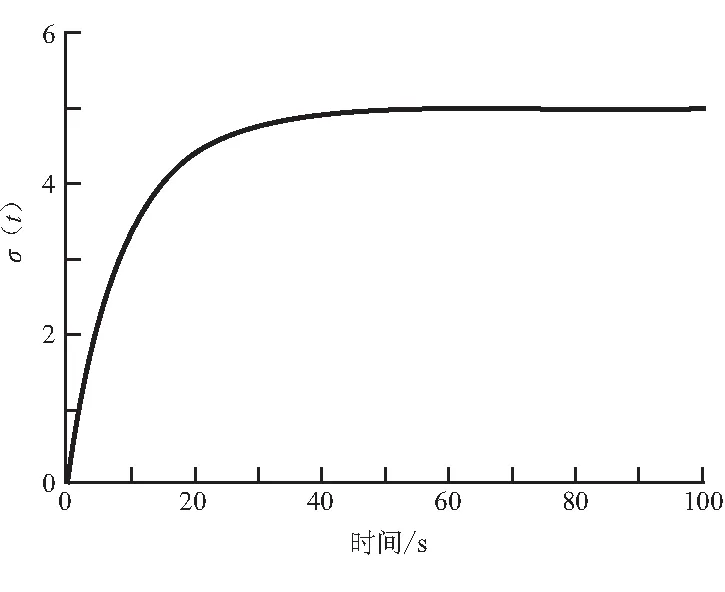
式(12)的函數形式可描述多種不同形態的變化關系。例如,當b=5、c=0.1及a=-0.01時,式(12)可描述先增加后減小的形態,如圖6(a)所示;當b=5、c=0.1及a=0時,式(12)可描述先增加、然后基本保持不變的形態,如圖6(b)所示;當b=5、c=0.1及a=+0.01時,式(12)可描述單調增加的形態,如圖6(c)所示。需要特別指出的是,這三種基本形態幾乎涵蓋了常應變率實驗結果中應力隨時間變化的各種規律,因而可用來刻畫應變率對材料性能的影響。
3 非線性粘彈性本構關系的應用
3.1 本構參數識別方法
由于具有應變率相關性,雖然與線性粘彈性本構關系具有相同的函數形式,但非線性粘彈性本構關系的材料參數不能再借助于松弛實驗獲得,而是通過常應變率實驗結果擬合得到,以實現更寬應變范圍或整個變形過程中與實驗結果一致。

Step-1:將給定應變率下的應力-時間實驗結果準備成Excel格式;
Step-2:在MATLAB軟件的Curve Fitting中自定義形如式(12)的函數;
Step-3:將Step-1中Excel格式的實驗結果通過Import Data接口輸入到MATLAB中;
Step-4:啟動MATLAB中Curve Fitting的Fit功能,獲得式(12)中參數a、b和c的值;
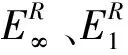

(a)先增加后減小的形態
(b)基本保持不變的形態

(c)單調增加的形態
3.2 常應變率拉伸實驗預測
某環境溫度下不同常應變率時的實驗結果如圖7中實線所示。
按照3.1節中的參數識別方法,根據圖7的實驗曲線,對式(12)中的3個參數a、b和c分別進行識別,再利用式(12)預測得到圖7中虛線所示的理論值。可以看出,非線性粘彈性本構關系在0.000 1~0.1 s-1的5個不同常應變率條件下,100%應變范圍內,預測的應力-時間關系都與實驗結果吻合良好。
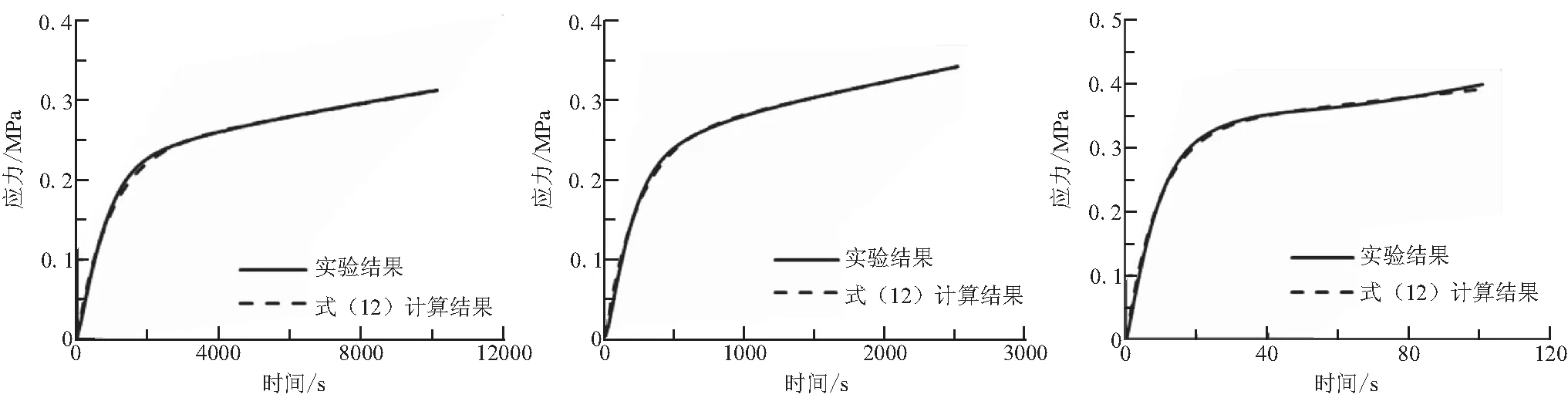
(a) 應變率為0.000 1 s-1 (b) 應變率為0.000 4 s-1 (c) 應變率為0.01 s-1
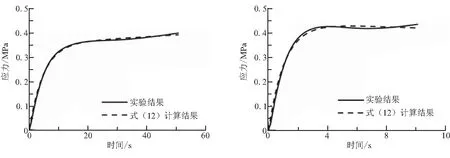
(d) 應變率為0.02 s-1 (e) 應變率為0.1 s-1
3.3 參數值統計
按照3.1節方法識別得到的函數參數和根據式(14)反演得到的非線性材料參數如表1所示。
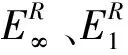
(15)

表1 識別得到的3個非線性材料參數值Table1 Identified values of the three nonlinear constants
將式(15)通過式(11)代入式(9),最終得到某溫度下考慮應變率效應的非線性粘彈性本構關系為
(16)
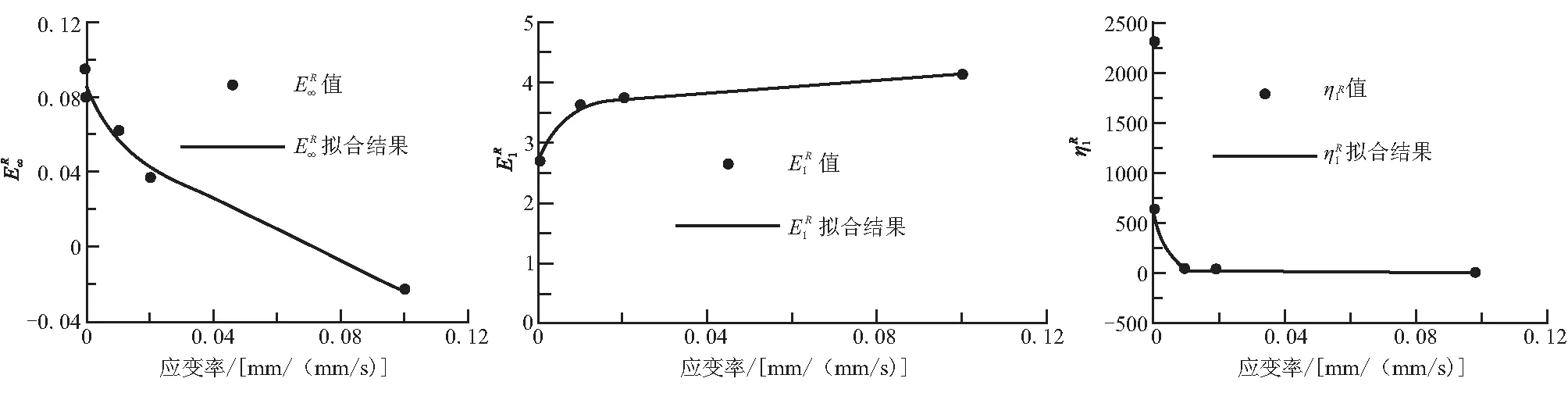
隨應變率變化隨應變率變化隨應變率變化
3.4 討論
應力-時間的關系(式(12))具有如圖6所示的基本變化形態,但是,圖7(e)所示的實驗曲線在應變較大時呈現出了略微的起伏變化,因而,與其他相比,式(12)對圖7(e)變化的描述尚待進一步改進。
實際上,在式(12)基礎上再增加一項,可使應力-時間關系變為
σ(t)=at+b(1-e-ct)+nt2
(17)
利用3.1節的識別方法和圖7(e)的實驗數據,得到函數參數值分別為

(18)
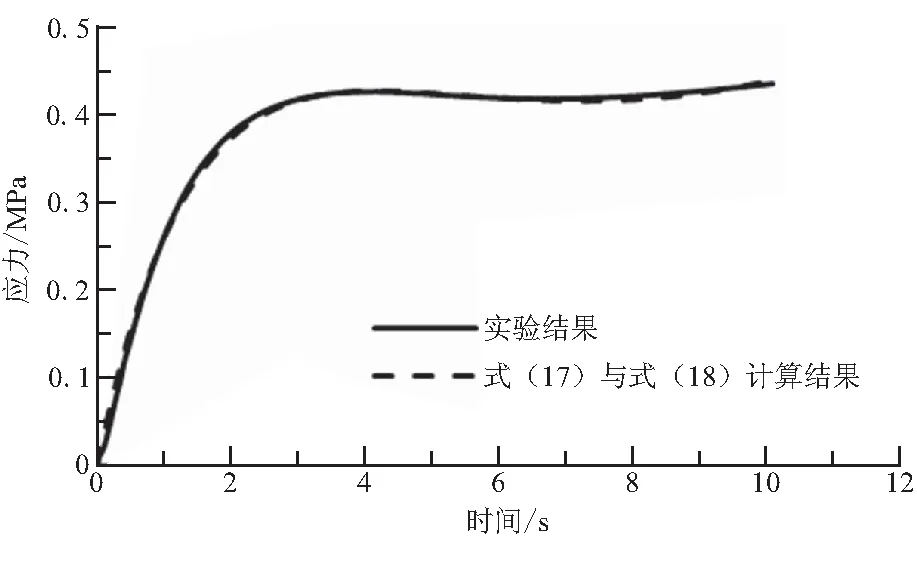
圖9 式(17)的改進預測結果Fig.9 Improved prediction by Eq.(17)
式(17)的預測與實驗結果比較如圖9所示,與式(12)預測值(圖7(e)中的虛線)相比,式(17)的預測(圖9中的虛線)與實驗結果符合更好。
此時,令
(19)
對式(19)兩邊求導得材料的非線性松弛模量:
(20)
但式(20)再不能像式(14)那樣反演得到具有明確物理意義的材料參數。但從實際使用角度,數量很有限的唯象參數a、b、c及n仍可方便地用于實際的工程結構分析。
4 結論
(1) 對因應變率引起的非線性粘彈性行為,可通過引入材料的非線性松弛模量概念,由線性粘彈性本構關系發展成為非線性粘彈性本構關系。
(2) 非線性本構關系的材料參數雖然由實驗數據唯象地擬合得到,但在物理上可解釋為三參數固體中的非線性彈簧系數和非線性粘壺系數。
(3) 應變率效應可用較少(例如3個)的材料參數對整個變形過程予以描述,符合工程領域設計的簡單性要求。
由于實驗數據量的限制及較大的應變率跨度,本文非線性粘彈性本構關系材料參數隨應變率的變化規律尚不明晰,需要更多實驗的支持。實際上,假以豐富的大溫度范圍多個常應變率拉伸實驗數據,本文非線性粘彈性本構關系的研究思想也可進一步延伸,以考慮對推進劑材料性能顯著影響的溫度因素。

