風力發電機變槳連接螺栓斷裂故障診斷研究

高培昱 ，程 珩 ，賴 成 ，何文龍

（1.太原理工大學 新型傳感器與智能控制教育部與山西省重點實驗室，山西 太原 030024；2.太原理工大學 機械工程學院 機械電子工程研究所，山西 太原 030024）

1 引言

高強度連接螺栓常用于風力發電機組的重要連接結構中，伴隨著大型化和工作環境惡劣使得連接螺栓的工作強度增加，連接螺栓斷裂故障經常發生[1]。目前相關方面的研究主要集中于對其線性的強度分析和壽命預測，常用的方法有如下的兩類：一種是數值分析方法，另一種是工程類算法[2]。關于螺栓的疲勞強度方面，文獻[3]中針對軸承與葉根的連接螺栓，基于葉素定理提出了一種疲勞強度的強度分析方法。文獻[4]中針對葉根連接螺栓進行接觸分析，可以精確計算螺栓和輪轂的應力。在疲勞壽命相關方面，文獻[5]中定性地提出結構的疲勞壽命和連接系統形狀的變化或缺陷有關。而實際的風力發電機組變槳系統連接螺栓數量多，結構尺寸比較大，需要考慮的非線性因素多，導致以有限元為主的數值分析方法計算量巨大，分析所得結果存在許多不確定因素[6]。上述研究存在的問題是沒有考慮這種外界載荷和螺栓的應力之間的非線性關系，與實際螺栓受力情況不相符合，導致結果與實際情況相差較遠。目前關于高強度連接螺栓強度和壽命的工程類算法主要有以下三種：Petersen算法、VDI2230算法和Schmidt-euper算法[7]等。由于Petersen算法在外界拉力和螺栓應力的關系分析上沒有進行細劃分，所以計算結果不太準確。而VDI2330算法主要用于解決線性問題，而對于受力復雜的重要連接結構，存在許多非線性因素，故不太適用。Schmidtand-Neuper理論在工程上常用來解決結構強度和壽命等，但在連接螺栓的故障診斷方面應用較少。為解決高強度連接螺栓的故障問題提出基于schmidtand-Neuper算法的變槳連接螺栓斷裂的故障診斷研究。

2 Schmidtand-Neuper理論

Petersen算法是基于彈性力學通過大量的實驗得出的，并且主要針對L型、T型連接法蘭的失效問題研究[8]。Schmidtand-Neuper理論是在Petersen算法的研究基礎上，以法蘭某處作為支點，將連接系統受載出現裂縫時簡化成一個杠桿模型，如圖1所示。并根據法蘭螺栓連接系統剛度分配比例，建立起連接螺栓實際受力與外載荷的非線性關系，以解決非線性的法蘭連接系統的疲勞可靠性問題。

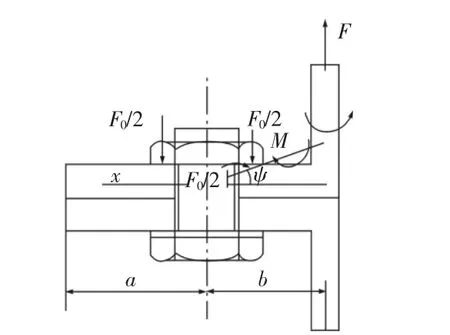
圖1 杠桿支點模型Fig.1 Leverage Fulcrum Model

3 Schmidt-Neuper算法建立

基于Schmidtand-Neuper理論模型，按螺栓數量將法蘭分成若干扇面，建立起單扇面的螺栓力學特性模型和算法。根據葉片根部筒壁主要受到葉根彎矩和葉根部垂向載荷作用，如圖1所示。以法蘭某一扇面為研究對象，其葉根薄壁受到的外載拉力為：

式中：F—外載拉力；M—連接法蘭某一截面彎矩；r—外載拉力F作用位置相應的半徑；N—螺栓總共的數目；Fz—葉片根部的軸向拉力。

根據圖1模型，法蘭螺栓連接系統可看作一組彈簧間的相互作用形成的。法蘭和墊片之間可看作是以串聯的方式連接的。其組合系統的等效剛度可表示為：

式中：KD.1—法蘭的剛度；KD.2—墊片的剛度。

連接系統中法蘭墊片和螺栓之間可看作是以并聯方式連接的，其組合系統的等效剛度[9]表達式為：

式中：KS—系統連接螺栓的剛度。

則連接系統中各個子系統剛度分配比例為：

式中：p—螺栓剛度占連接系統的比例；q—墊片法蘭組合系統剛度占總連接系統的比例；

引入剛度分配因子λ表達式為：

式中：a—螺栓幾何中心與法蘭內徑最小距離；b—螺栓幾何中心與葉根筒壁中心的最小距離。

設螺栓的預緊力為F′，根據圖1模型，法蘭間未出現縫隙的臨界狀態[10]時法蘭受到拉力F′為：

當法蘭間出現裂縫時且開始擴展時，法蘭上的受到的拉力F2為：

由此可得出法蘭外載與螺栓工作載荷對應關系，如表1所示。

表1 連接法蘭外載與螺栓工作載荷對應表Tab.1 Connection Flange and Bolt Working Load Corresponding to the Table

4 理論分析和測試試驗對比

4.1 實驗數據

由某風力發電機組公司提供的1.5MW級風力發電機組的故障機組葉片上法蘭連接系統基本參數包括：螺栓的規格為M30整圈的螺栓數量為54，材料屈服強度為900MPa，墊片的外徑為72mm，內徑為33.02mm，厚度為5.6mm，法蘭的外徑為1900mm，上下法蘭的厚度130mm，初次施加預緊力為250KN，a=50mm，b=42mm。

4.2 理論計算

假設葉片在旋轉過程中，在旋轉面上由于葉片自身重力作用導致受載螺栓在某側前緣位置的受拉力，同時法蘭變形釋放給螺栓增加了附加的作用力，而相對180°位置螺栓受壓，情況剛好相反，導致葉片旋轉過程中連接螺栓一個周期內軸向載荷變化較大。理論計算流程，如圖2所示。

圖2 計算流程圖Fig.2 Calculation Flow Chart

在理論計算時以兩種情況為例：出現間隙和未出現間隙。理論計算結果，如表2所示。

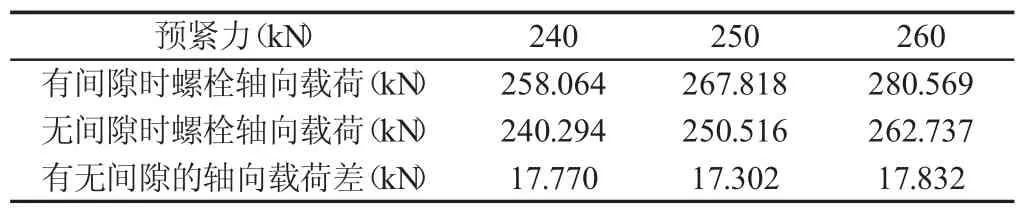
表2 受載螺栓理論計算結果Tab.2 Theoretical Calculation Results of the Loaded Bolt

通過表2可知：相同工況，不同預緊力作用下，有無間隙計算結果中軸向力差值較大，其均差值為17.635kN。說明法蘭間隙會導致法蘭變形，進而發生故障，理論分析的結果表明軸向力差值較大可能是導致風電法蘭連接系統螺栓斷裂故障的直接原因。

4.3 測試實驗

4.3.1 測點布置

為了驗證理論分析的合理性，對某風場的1.5WM風力發電機組故障葉片進行測試實驗，采用墊式壓力傳感器、信號處理模塊、無線信號采集和發射器聯合使用共同完成測試實驗，通過對故障機組現場觀察了解到，斷裂螺栓的位置集中在前緣部位，連接部位的截面分析，如圖3所示。

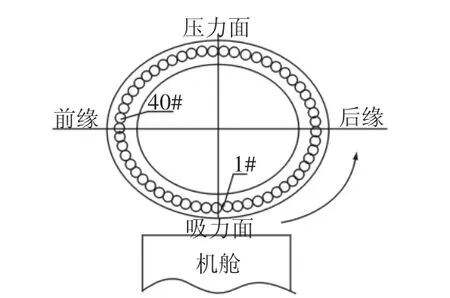
圖3 連接系統的截面Fig．3 Cross Section of the Connection System

為了方便統計，以逆時針方向對機組連接螺栓進行編號，機組螺栓發生斷裂的位置為1#和40#附近的螺栓，由于連接部位螺栓數量多，為避免資源浪費，故只對斷裂過的螺栓位置進行測試實驗。通過測試故障葉片在旋轉面上的不同位置處被測螺栓的受力情況，同時監測對比其他兩個正常葉片相同位置處螺栓的受載情況，讓風機分別在小風和大風工況下進行機組的啟停機、空載、正常運行等狀態測試。

4.3.2 測試條件

（1）安裝傳感器時，被測葉片應盡量朝上以減少螺絲受葉片重力的影響。（2）安裝過程中監控打力矩情況，盡可能在相同初始預緊力條件下進行測試。（3）在打力矩之前，對傳感器進行零點測試。

4.3.3 測試實驗機組運行狀態和風況

小風風況風速范圍為（2．8～3．2）m/s，機組狀態為連續運行。大風風況風速范圍為（8．5～12）m/s，機組狀態為啟動—運行。

測試結果，如圖4、圖5所示。（故障螺栓位于1葉片，2，3葉片均正常），結果統計，如表3、表4所示。

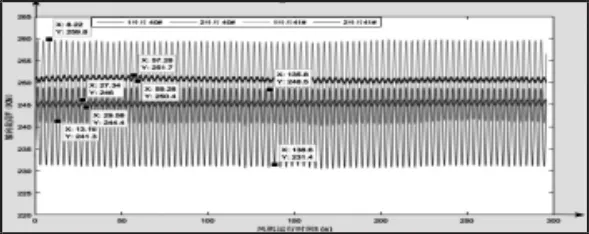
圖4 小風工況運行結果Fig．4 Operating Results Under Weak Wind Conditions

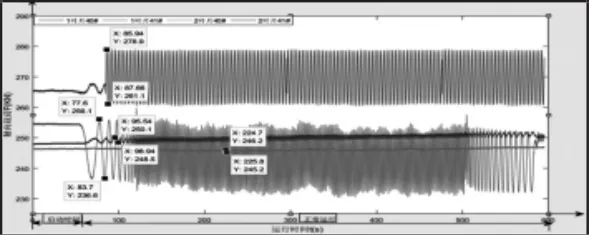
圖5 大風工況下運行結果Fig．5 Operating Results Under Strong Wind Conditions

表3 小風運行狀態下幅值差結果統計Tab.3 Wind Condition Amplitude Difference Statistics

表4 大風運行狀態下幅值差結果統計Tab.4 The Results of the Amplitude Difference Under the Condition of Strong Wind

4.4 分析結果

通過對比表2、表3、表4，可以得到以下分析結果。（1）在風機葉片整個運轉過程中，螺栓所受軸向載荷呈現周期性的變化，大風運行狀態下，由于風機葉片旋轉加快，所以載荷波動周期變小，但是波峰波谷的幅值差仍然保持相似的特征。（2）正常機組葉片連接螺栓在運行過程中所受的軸向載荷變化較小，而故障螺栓所受的軸向載荷有較大的波動，波峰波谷幅值差較大。（3）理論分析計算得到有無間隙情況下，螺栓所受軸向力差值均值為17．635kN，實驗測得結果顯示，軸向力幅值差均值為18．65kN，二者相差1．015kN，占實測結果的5%，在誤差允許的范圍內，可見法蘭故障導致的軸向力幅值變化過大是導致螺栓斷裂的直接原因。

5 結論

通過理論分析與實驗結果對比，驗證了Schmidtand-Neuper算法在此應用的合理性，找出法蘭間存在間隙是導致變槳連接系統連接螺栓斷裂的直接原因，結果表明了所提出的分析方法和流程對這種高強度法蘭螺栓連接系統故障診斷具有合理性、可行性。