風(fēng)電機組齒輪箱分階段機會維護策略研究

范思遐，吳 斌，李友釗

（1.上海電機學(xué)院 商學(xué)院，上海 201306；2.上海電機學(xué)院 電氣學(xué)院，上海 201306）

1 引言

根據(jù)國家能源局在《風(fēng)電發(fā)展“十三五”規(guī)劃》做出的指示，未來風(fēng)電行業(yè)不僅有著總裝機量的要求，其機組的運維優(yōu)化也被提上議程。作為海上風(fēng)電度電成本的主要影響因素之一，降低運維成本的重要性不言而喻。盡管風(fēng)電機組失效故障與停機時間獨立分布，但海上風(fēng)機50%的停機維修活動是主要由于齒輪箱故障失效導(dǎo)致[1]。因此對齒輪箱進行健康管理是風(fēng)電場運維活動的一個重要環(huán)節(jié)。

目前，對齒輪箱維護多為無計劃或者低效率計劃的維護，一般是待齒輪箱的狀態(tài)衰退至一定程度后才進行維修。這類維護策略雖然在傳統(tǒng)的維修上作出了適應(yīng)性改進，便于開展，然而沒有彈性的維護計劃易造成資源浪費，增加度電成本。因此，尋找“過度維護”與“維護不足”之間平衡點顯得尤為重要。國內(nèi)外也發(fā)展了很多針對齒輪箱等設(shè)備的預(yù)防性維護策略研究[2-6]；有學(xué)者提出隨役齡增加，維護期逐漸變短的維護策略[7-8]；由于海上風(fēng)機維護會隨階段不同具有不同的維護策略，應(yīng)論證一種符合階段特點的維護策略。

利用搭建的風(fēng)機模擬平臺進行退化狀態(tài)評估實驗，劃分出四個退化區(qū)間，以此建立了分階段的機會維護模型，并給出了各部件的具體維護動作及單位時間維護成本，驗證了分階段機會維護的合理性。

2 海上風(fēng)機齒輪箱階段性機會維護策略的建立

按照維修經(jīng)驗，風(fēng)機齒輪箱的維護策略大致可以分為三種：反應(yīng)性維護，預(yù)防性維護，預(yù)測性維護。

2.1 基于部件維護經(jīng)濟相關(guān)性

在實際風(fēng)電場運維活動中，針對不同部件安排各自檢修周期具有不可操作性，作為多部件構(gòu)成的復(fù)雜系統(tǒng)，考慮到部件之間存在著維護經(jīng)濟相關(guān)性，故將風(fēng)機齒輪箱的幾個關(guān)鍵部件（A，B，C，D…）作為一個維護組，假設(shè)其間發(fā)生失效的概率是互不相關(guān)的，則機會維護的表述與假設(shè)應(yīng)如下：

（1）齒輪箱各部件的狀態(tài)是可以實時監(jiān)測的，當(dāng)不可回復(fù)故障發(fā)生時立即停機維修（最小修復(fù)），否則在預(yù)定維護時間點時進行維護（i表示第i次維護活動），部件的失效率函數(shù)符合Weibull比例失效模型，且部件間不存在拆卸順序相關(guān)性及隨機相關(guān)性；

（2）部件A作為主要維護部件，當(dāng)其可靠度衰退到維護閾值Rp時，對齒輪箱開展維護活動，其它部件獲得了同期進行維護的機會：部件可靠度RA（i）處在機會維護上限Rom內(nèi)，則對其進行維護；

（3）在維護時間點，部件A的維護動作包括不完全維護（flag=1）與完全維護（flag=2），為決定采用何種維護動作，引入維護回報率的概念：當(dāng)前維護動作的投入成本C與機組可靠度提升ΔR的比值ROIA（i）來判斷；維護組中其他部件B，C，D…的維護動作則包括三種，分別為不完全維護、完全維護、不維護（flag=3），判斷條件與部件A類似[9]；

（4）限制條件，即維護次數(shù)上限Nm，以及置換閾值Rrep。

2.2 傳統(tǒng)齒輪箱維護策略

在傳統(tǒng)的策略考慮中，并沒有對齒輪箱退化狀態(tài)進行分段，更多是依靠經(jīng)驗常識對設(shè)備的健康狀況進行劃分，缺乏科學(xué)性。

經(jīng)驗數(shù)據(jù)表明，風(fēng)電機組齒輪箱在初始安裝階段故障率最高，而隨著役齡增加，故障率急速下降，直至度過試運營期，其失效率h（t）比較穩(wěn)定的處于一個較低的水平上，因此可用失效率的積分，即可靠度R（t）作為齒輪箱狀態(tài)指標(biāo)；而到了后期長時間的運行導(dǎo)致齒輪箱各部件發(fā)生磨損、疲勞、老化等耗損現(xiàn)象嚴(yán)重，部件的狀態(tài)開始急速衰退，使得失效率又開始上升[10]。故在齒輪箱試運行期以后的時間段，開展多個部件分階段機會性維護動作，其退化趨勢在每個退化階段內(nèi)有所差異。具體的維護示意圖，如圖1所示。

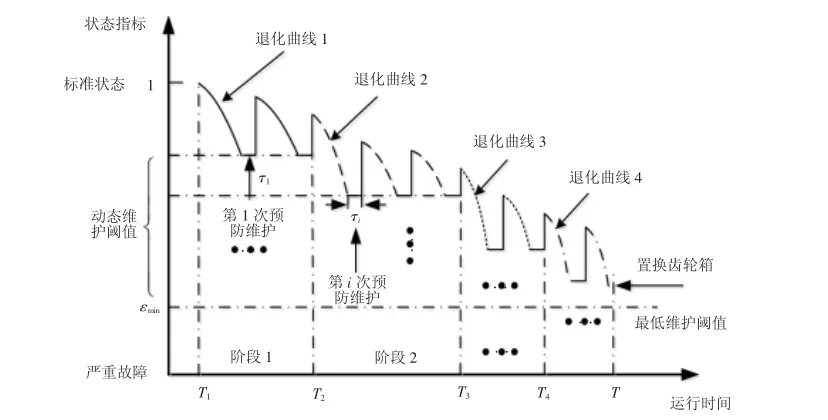
圖1 風(fēng)電機組齒輪箱分階段維護示意圖Fig．1 Phased Maintenance Diagram of Wind Turbine Gearbox

3 齒輪箱階段性機會維護模型搭建及求解

3.1 齒輪箱退化狀態(tài)階段數(shù)優(yōu)化

退化矩陣描述了齒輪箱在整個壽命區(qū)間內(nèi)的退化特征，為有效將這些特征向量劃分到不同的分類器中，采用K-means聚類分析法將其分別劃分出（3～7）個聚類數(shù)目，然后計算各數(shù)目下的Scat-Sep（最小類內(nèi)緊密度—最大類間分離度）指標(biāo)，對應(yīng)該指標(biāo)最小的聚類劃分即為最佳退化階段數(shù)目。

假設(shè)分類器用 C［k］=｛C1，C2，…，Ck｝表示，其中 k 為總聚類數(shù)目，則類內(nèi)緊密度指標(biāo)Scat（C［k］）用類內(nèi)各數(shù)據(jù)之間歐氏距離的平方和來描述，類間分離度指標(biāo)Sep（C［k］）用類與類之間的距離來描述，即類別間點對的平均距離：

式中：k—第k個分類器；

xm，xn—類Ci內(nèi)的任意兩個數(shù)據(jù)點；

y—類Cj內(nèi)的數(shù)據(jù)點；

考慮到兩者的取值范圍并無差異，故組合參數(shù)α取為1，組合平衡函數(shù)為：

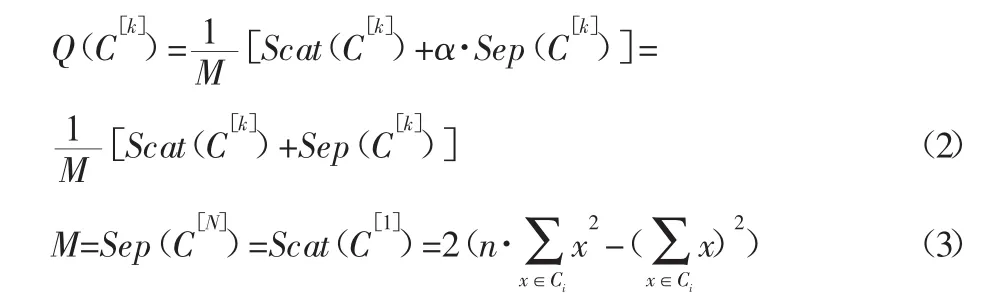
式中：M—兩指標(biāo)平衡系數(shù)，其值等于最大聚類（每個類別只含一個樣本點）時的類間分離度指標(biāo)，或者最小聚類（唯一聚類）時的類內(nèi)緊密度指標(biāo)。

3.2 齒輪箱分階段機會維護模型

模型建立的關(guān)鍵是確定各部件的維護動作，根據(jù)動作不同將部件分為兩類，一類是主維護部件A，另一類是機會維護部件B，C，D，...，引入維護動作標(biāo)記符號如下：

3.2.1 單位時間維護成本

以風(fēng)機齒輪箱階段性預(yù)防維護策略所跨時間段內(nèi)單位時間維護費用Cut最小為決策依據(jù)，介紹計算Cut的方法。

（1）維護停機損失Cs：維護活動造成的發(fā)電量損失可根據(jù)同期平均風(fēng)機功率Pave、電價p以及停機時間ts決定，將等待時間tw也加入到停機時間中[6]。從而有下列式：

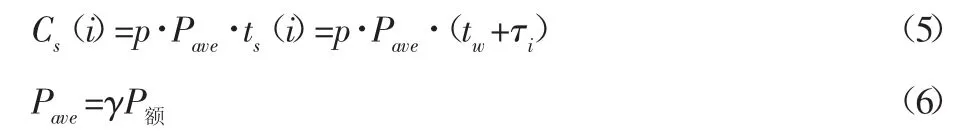
式中：γ—風(fēng)電機組同期發(fā)電容量因子；

τi—第i次預(yù)防維護動作所用時間。

（2）維護成本：齒輪箱的維護成本包括三個部分，部件置換成本Crep、不完全維護成本Cinc以及最小修復(fù)成本Cminr。理論上來說，預(yù)防維護的投入資源越多其維護效果就越好，維護后部件的可靠度就越有保障，因此不完全維護成本應(yīng)該與部件可靠度函數(shù)的該變量 ΔRi有關(guān)，則：Cinc（i）=K（ΔRi）μ

總維護成本Cme就可以用下式表示：

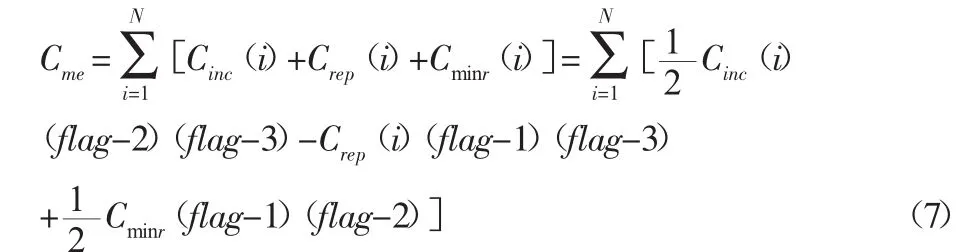
（3）維護耗材成本與運輸?shù)跹b成本Ctrn。維護（包括最小修復(fù)與不完全修復(fù)）與置換所用到的運輸成本，及運維人員工資一并算入運輸?shù)跹b成本中。模型的決策依據(jù)為單位維護時間內(nèi)成本最小，故有：

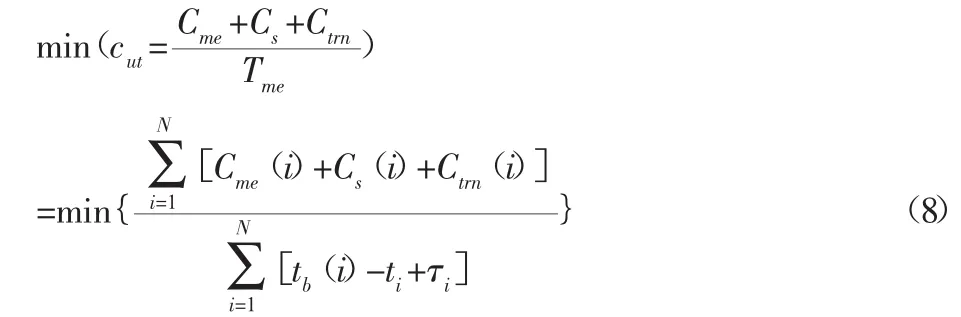
3.2.2 具體維護動作的判斷

維護回報率可用下式計算：

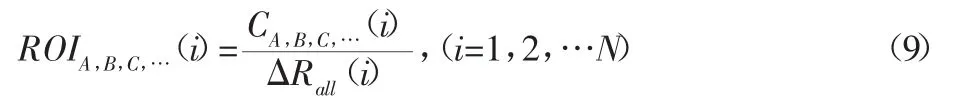
式中：CA，B，C，…（i）—部件 A，B，C，…第 i次維護動作的維護成本；ΔRall（i）—部件第i次維護動作執(zhí)行后風(fēng)電機組的可靠度改善情況。

計算flag置不同值時的維護成本，從而求得對應(yīng)的維護回報率ROI，根據(jù)下式判斷維護動作：

4 實驗驗證及數(shù)據(jù)分析

4.1 齒輪箱退化實驗

為探究風(fēng)電機組齒輪箱退化過程，搭建實驗?zāi)M平臺，如圖2所示。其中齒輪箱的傳動比為1：1．36；0．5kW 的磁粉制動器作為負載；變頻調(diào)速三相異步電機作為動力源；變頻器分辨率達到0．01Hz；齒輪箱振動信號的采集利用MPS-140401信號采集卡。三相電機頻率設(shè)定f=20Hz，即轉(zhuǎn)動一周期需0．1s，MPS采樣率設(shè)定為16000Hz，每半小時采集一次數(shù)據(jù)，每次持續(xù)采樣時間為30s，共采集了900組有效數(shù)據(jù)，每組數(shù)據(jù)切取三個振動樣本。對這2700組信號進行小波包分解后，提取能量譜作為齒輪箱的退化矩陣，然后用Scat-Sep評價指標(biāo)對各聚類數(shù)目下的特征向量進行分析計算，其結(jié)果如表1所示。可以看出齒輪箱的退化過程為四個階段時，平衡函數(shù)取到了最小值 0．5311。

圖2 實驗臺設(shè)置Fig．2 Experimental Platform

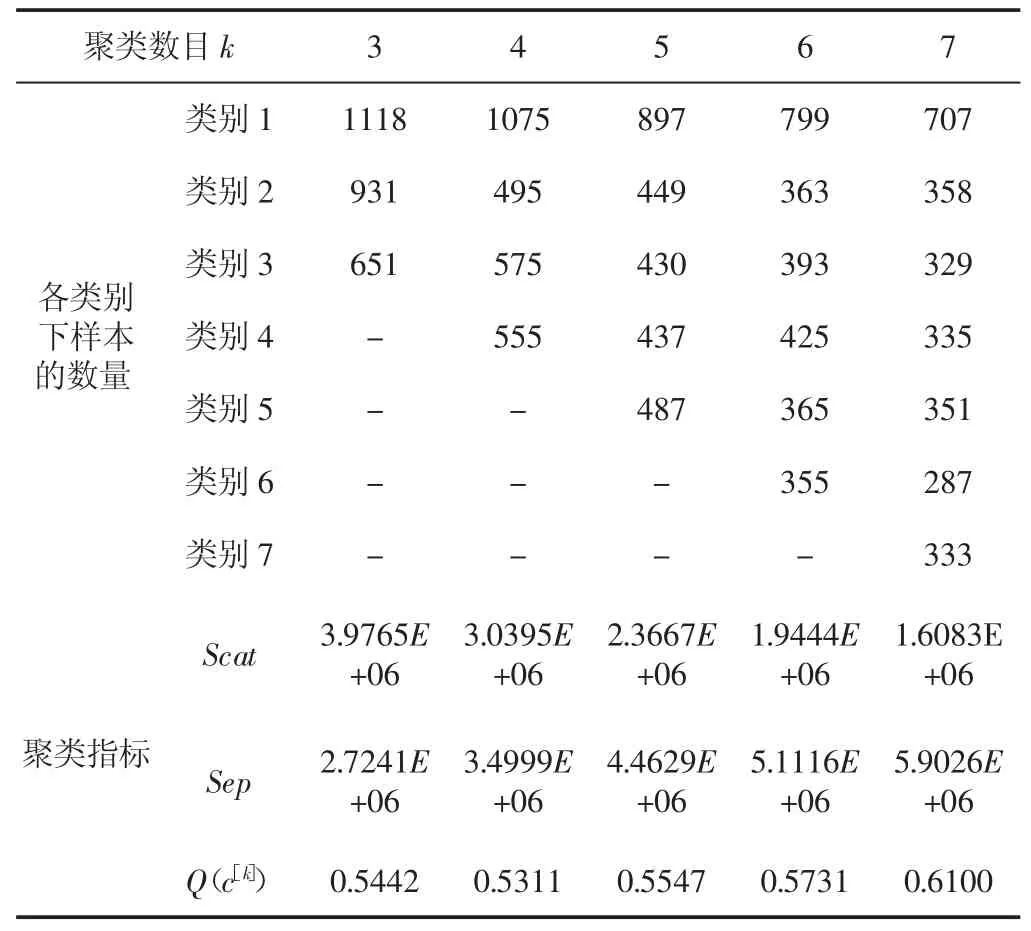
表1 不同聚類數(shù)目下各評價指標(biāo)Tab.1 Evaluation Indexes Under Different Cluster Numbers

4.2 齒輪箱階段性機會維護模型算例驗證

4.2.1 模型參數(shù)設(shè)置

以某兆瓦級風(fēng)電機組為研究對象，將傳動系統(tǒng)的主軸、主軸軸承、齒輪副、從動軸軸承四個部件納為一個機會維護組，其初始參數(shù)，如表2所示。分四個階段進行維護。完全維護成本相關(guān)系數(shù)K直接取Crep，部件的運輸?shù)跹b費用Ctrn取15萬元與25萬元（維護動作與置換動作），多部件吊裝運輸費用增加系數(shù)k取0．13，預(yù)防維護平均等待時間取72h，平均預(yù)防性維護時間15h，平均完全維護時間40h，停機損失發(fā)電量電價0．9元/（kW·h），同期發(fā)電量容容量因子 γ 取 0．7、0．6、0．5、0．4 四個等級，狀態(tài)回復(fù)因子 λ 取 0．75、0．7、0．6與0．5四個等級，役齡回退因子a＝i/（3i+18），可靠度遞減因子b=（18i+1）/（19i+1），不完全維護成本相關(guān)因子μ取0．8、0．75、0．7、0．7。考慮到維護閾值變化使得維護間隔不確定，故每個維護階段留有一定的時間裕量 ΔT=50d，取各階段初始維護閾值為 Rp=［0．950．930．90 0．85］，時間跨度為 2179d、1002d、1166d、1128d。

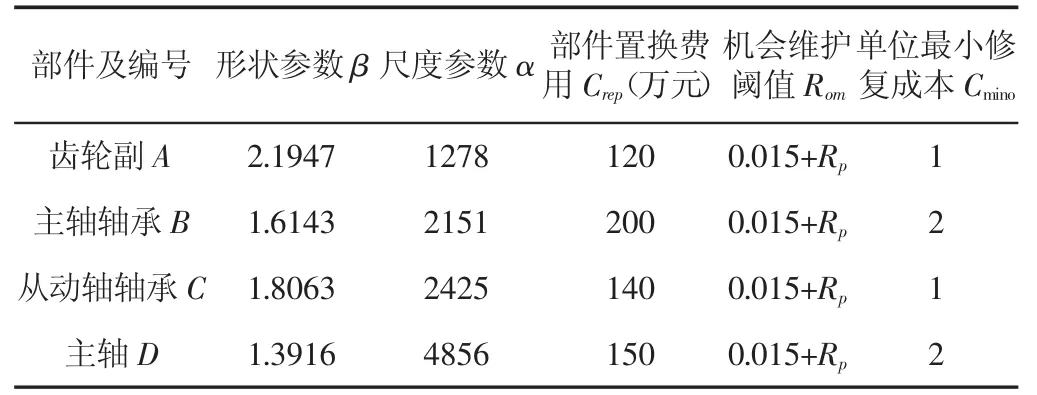
表2 機會維護組各部件初始參數(shù)Tab.2 Initial Parameters for Each Part of The Opportunity Maintenance Group

4.2.2 階段性機會維護時間間隔及動作判斷

部件A的維護時間間隔以及所處維護階段，如表3所示。從表中可以看出，在維護后期，階段性的動態(tài)維護閾值很好的解決了維護間隔短這個問題，該結(jié)果與實際風(fēng)場每年（1～2）次的維護計劃更為符合。

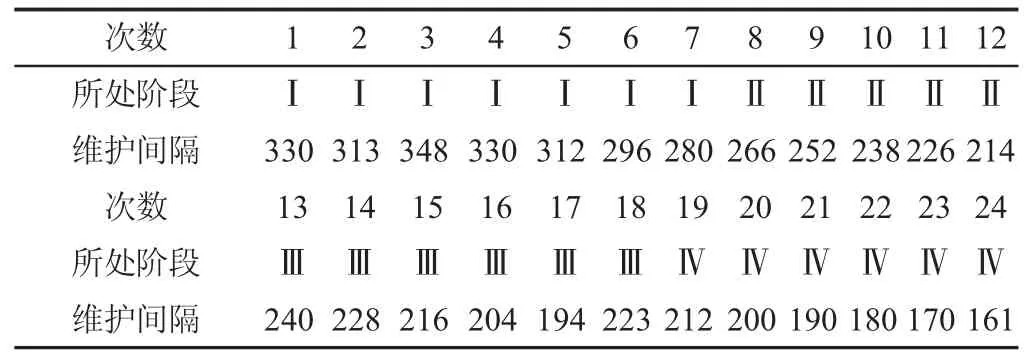
表3 部件A階段性預(yù)防維護時間間隔Tab.3 Part A Phased Preventive Maintenance Time Interval

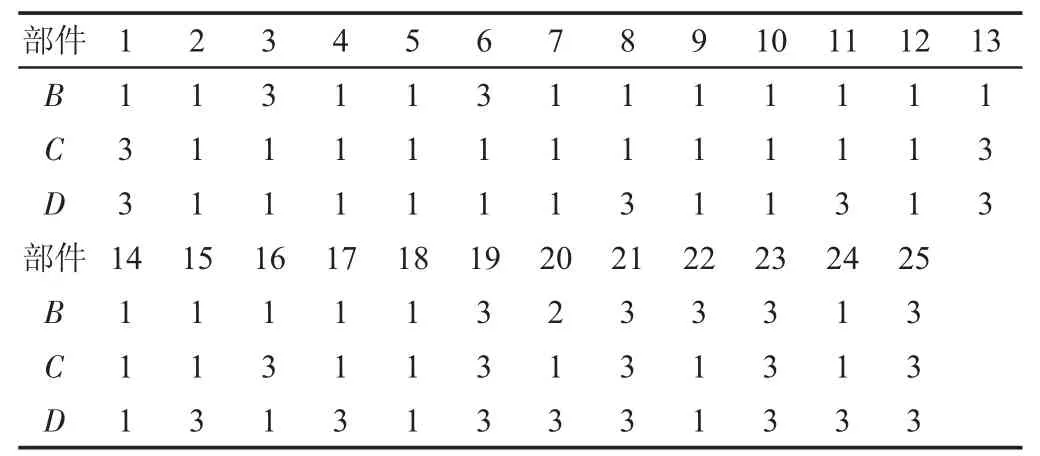
表4 各部件分階段預(yù)防性維護動作Tab.4 Phased Preventive Maintenance of Each Component

階段性機會維護策略下的各部件預(yù)防性維護動作，如表4所示。對應(yīng)的單位時間機會維護成本為（1.0504e+03）元/天，較不分階段的機會維護策略的單位時間維護成本（1.5110e+03）元/天有了很大的降低。

4.2 .3兩種機會維護策略對比

為了更直觀的比較齒輪箱階段性機會維護策略與傳統(tǒng)機會維護策略兩者之間維護動作及經(jīng)濟性的差異，選取兩種維護策略第6次預(yù)防性維護為例，比較兩者之間的差異以便說明機會維護動作的決策過程，判斷結(jié)果，如表5所示。

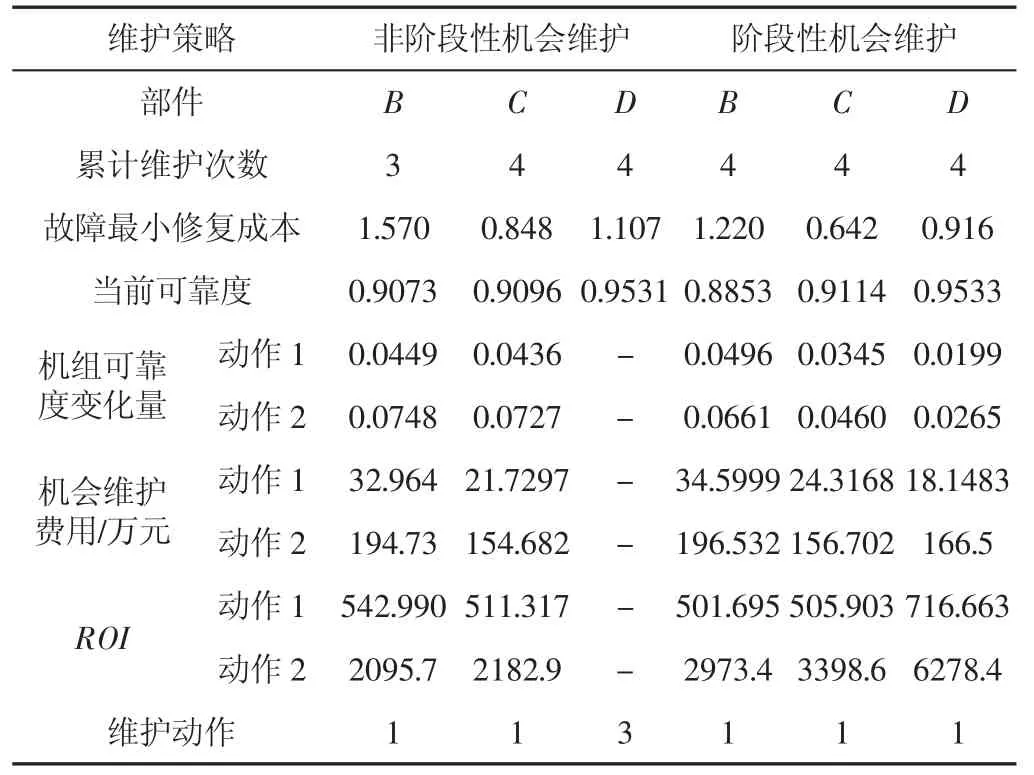
表5 兩種維護策略第6次維護動作對比Tab.5 The Sixth Maintenance Actions Comparison of Two Maintenance Strategies

表中：非階段性機會維護策略的維護閾值設(shè)為0.93。

在不考慮階段性機會維護策略中，部件D在第6次預(yù)防維護開始前可靠度為0.9531，故沒有達到進行機會維護的條件，因此不進行維護動作；而在階段性的維護策略中，部件D的可靠度為0.9533，雖然與非階段性維護策略中的部件可靠度近似相等，但是其可靠度RD=0.9533卻處在進行機會維護的范圍內(nèi)（Rom=0.965），因此進行機會維護動作；同時，兩個不同的維護策略中，前者的故障最小修復(fù)成本較前者更高；從各部件的維護回報率也可以看出，分階段的預(yù)防性機會維護策略的ROI更小，這意味著投入相同的維護資源機組可以更好的改善可靠度，部件的到了充分的維護，特別是到了維護后期，很好的平衡了傳統(tǒng)維護策略的“維護不足”與固定維護閾值機會維護策略后期的“過度維護”問題。

5 結(jié)語

針對海上風(fēng)電機組齒輪箱的實際衰退特性，提出一種基于動態(tài)維護閾值的機會維護策略，表現(xiàn)為整個維護策略是按階段進行展開的，動態(tài)維護閾值和固定維護閾值的差異就在于前者更好的適應(yīng)了齒輪箱隨役齡增加可靠度加速下降的特性，改善了部件的維護回報率。