基于Eshelby-Stroh公式各向異性彈性體接觸問題研究

顏燈燈，李成剛，*，申景金，王艷，王春明，宋偉山

(1.南京航空航天大學 機電學院，南京210016; 2.南京郵電大學 自動化學院，南京210023)

壓頭與彈性體之間平面問題的研究在工程力學中有著廣泛的應用，通過建立載荷與壓痕深度或變形曲線等參數之間的數學模型，再依據壓痕試驗便可以測量材料的力學性能。隨著對壓頭和彈性體接觸問題的研究不斷深入，壓痕試驗被廣泛應用于軟骨組織的彈性模量測量［1］、生物組織的性能評估［2］和力學性能測量［3］、微創手術用的觸診探針［4］、弱錘沖擊初始損傷試驗［5］等方面。近年來，使用原子力顯微法的壓痕試驗技術成為量化軟質材料和生物材料力學性能的重要技術［6-7］。

在許多應用中，壓頭的彈性模量要比被壓彈性體的大很多，因此壓頭一般都被視為剛體。被壓的彈性體視為固定在一個剛體的基座上，即彈性體的其中一面完全固定。當壓痕深度相對于彈性體的厚度、寬度以及壓頭某些參數來說比較小時，彈性體的變化可以視為是線性變化的。

平面壓痕問題是混合邊界值問題，多年來有著眾多的研究。Muskhelishvili和England等使用解析延拓的方法求解典型結構壓頭的接觸問題［8-9］，Gladwell和 England 使用特定的正交多項式展開的方法解決混合邊界值接觸問題［10］，Okumura等利用有理映射函數和復應力函數分析平面壓痕問題［11］。上述研究面向各向同性的彈性材料，若將對象拓展到各向異性材料，求解方法變得復雜。結合Muskhelishvili［8］的解析延拓方法，使用Eshelby-Stroh公式可以求解任意輪廓的平面壓頭與各向異性彈性半空間體的接觸問題［12-13］。Hwu和Fan基于Eshelby-Stroh公式和解析延拓，并使用共軛梯度法研究壓頭與各向異性彈性半空間體的接觸問題［14-15］，可以考慮壓頭與彈性體之間的摩擦。Batra和Jiang基于Eshelby-Stroh公式設定級數函數表示位移函數和應力函數，研究了圓柱壓頭和平頭的接觸問題，根據接觸寬度求解各處的位移和應力［16］。Jiang和Batra依據Eshelby-Stroh公式，改變了級數函數的形式，研究壓頭與內含缺陷的彈性體之間的接觸問題［17］。

基于Eshelby-Stroh公式，可以求解邊界條件較為復雜的接觸問題，但是應力往往要比位移收斂得慢［18］，在級數項數較少時求解載荷值誤差較大。為了獲取較為準確的計算結果，計算過程中要設定較大的K值(函數中級數的項數)。本文提出使用整體位移約束法和線性迭代，提高求解結果的收斂性，在選擇較小的K值時求得更加準確的計算結果。

1 接觸問題分析

如圖1所示，本文要研究的是各向異性的彈性體與凸面型壓頭接觸作用的平面問題。各向異性材料的彈性體在x1軸上長L，在x2軸上高h。假設凸面型壓頭和彈性體在x3軸方向上(垂直于紙面向外)的長度相比于紙面上的參數(如長L、高h)足夠大，凸面型壓頭受到載荷P，沿x2軸負方向垂直壓入彈性體，記壓頭壓入的深度為D，接觸寬度為2c，壓頭與彈性體發生接觸的高度為d，則有非接觸高度u0=D－d。圖中的凸面型壓頭是一個倒圓角的楔形。其中，楔形的斜度為θ，圓角半徑為R。根據剛體壓頭有無與彈性體發生接觸，可將彈性體按“豎直虛線”劃分為Ⅰ、Ⅱ和Ⅲ三部分。

在直角坐標系下，彈性體各處的位移、應力和應變可以表示為關于x1和x2的函數。在不考慮彈性體自身重力時，存在以下關系:

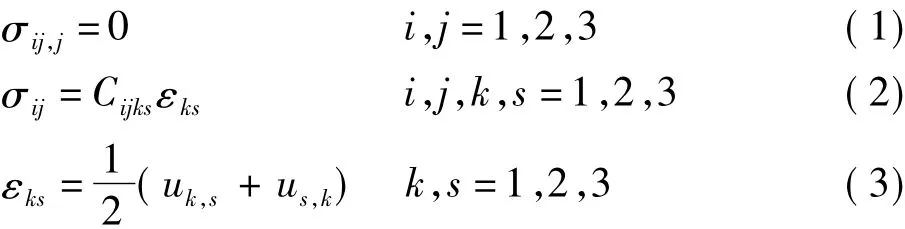
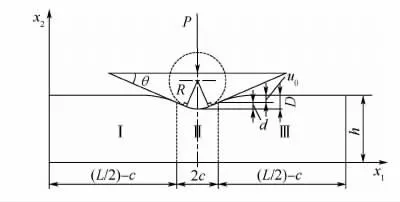
圖1 壓頭與彈性體的接觸模型Fig.1 Contact model of indenter and elastic body

式中:應力 σij= σji，σij，j= σij/ xj;εks為應變;uk為在 xk方向上的位移;uk，s為 uk對 xs求導;Cijks為彈性體的材料參數，滿足全對稱性:

將式(3)代入式(2)并照式(1)求導可得

參照圖1中的接觸模型，彈性體的底部固定，左右兩側自由，頂部在中間長度2c區域發生接觸。由此可得邊界條件為

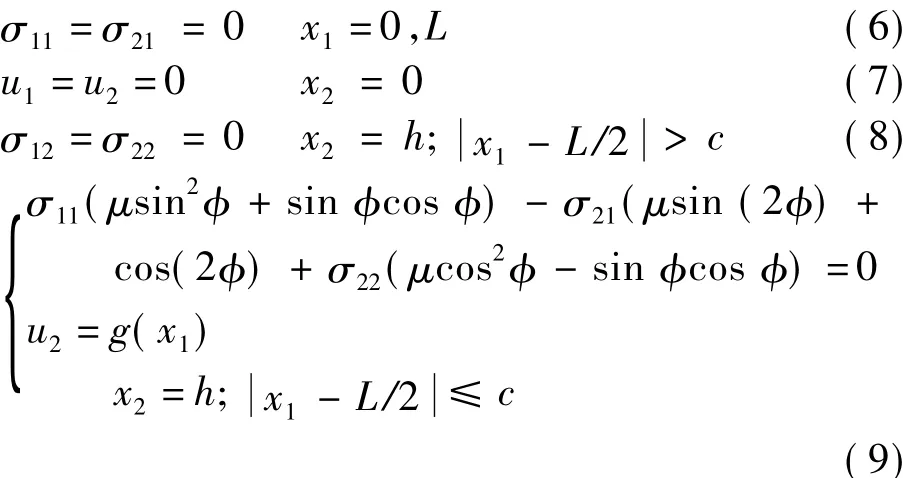
式中:μ為剛體壓頭與彈性體之間的摩擦系數; 為剛體壓頭與彈性體接觸的切向角，該公式由切應力和正應力的平衡關系得到。若將剛體壓頭與彈性體之間的摩擦視為0，則有

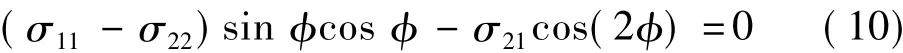
對于圖1中倒圓角的楔形，以區域Ⅰ和區域Ⅱ頂部的交接處為原點，x1和x2方向與圖1中的坐標方向相同，則有外廓函數為

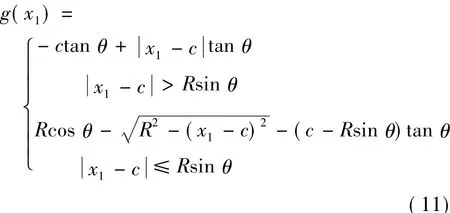
在研究小變形接觸問題時， 的取值較小時便可以忽略，因此軸向載荷P可表示為

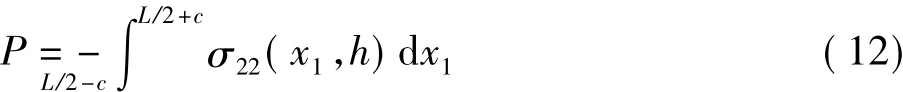
若考慮接觸點處的斜率，軸向載荷P可表示為

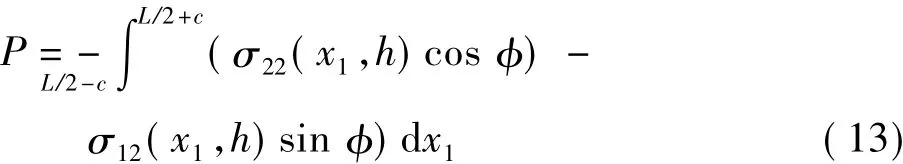
2 接觸問題的解析解

2.1 根據Eshelby-Stroh公式求解邊界值問題

假設彈性體的位移、應力和應變是關于x1和x2的函數，根據Eshelby-Stroh公式可以求解上述邊界值問題［19］。

首先假設

或

式中:f(z)為關于z的函數;ai可以根據材料參數求解;u和a分別為位移和位移參數。

其中:p為特征值。

將式(14)對xs求導可得

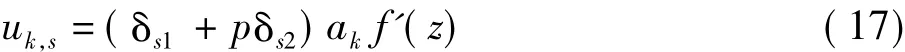
式中:δsi為克羅內克函數。再將式(17)對xj求導，后依據式(5)可得

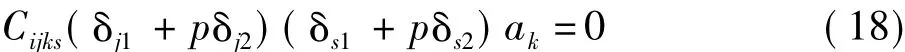
即

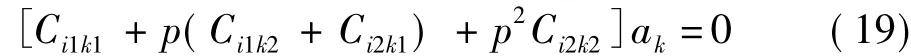
將式(19)寫成矩陣形式為

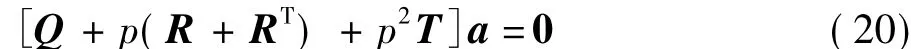
式中:Q、R、T都為3×3的矩陣，滿足

求解式(20)可以引入

式中:ζ為特征向量。

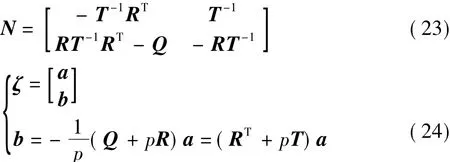
p為復數，6個p中，有3對是共軛復數。假定

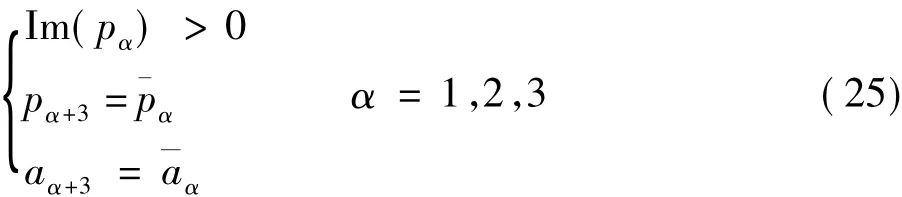
根據彈性體的材料參數，便可確定p和ai的值。根據式(2)和式(17)可得

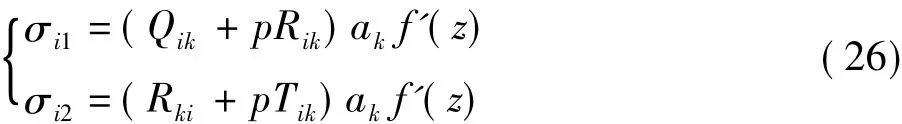
因此，可以得位移和應力表達式分別為

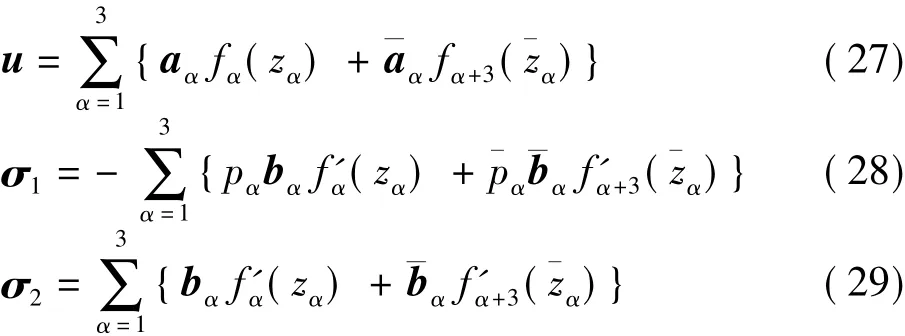
式中:σ1、σ2為應力。u、σ1、σ2都是 3 ×1 的列向量，且

在區域Ⅰ與區域Ⅱ的交接處和區域Ⅱ與區域Ⅲ的交接處滿足連續性條件:交接處左邊的位移和應力與交接處右邊位移和應力相等。將彈性體分成3個部分后，每一部分彈性體以其左下角為原點，不改變軸x1和軸x2的方向，則有

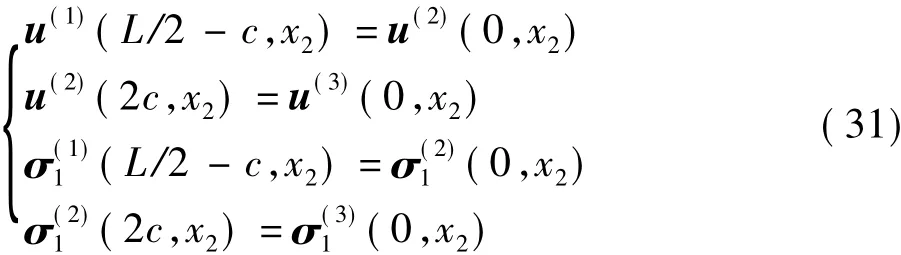
式中:u、σ1和 σ2右上角括號內的上標1、2、3對應彈性體Ⅰ、Ⅱ、Ⅲ。

假設每一部分組織的彈性體的f(z)函數為

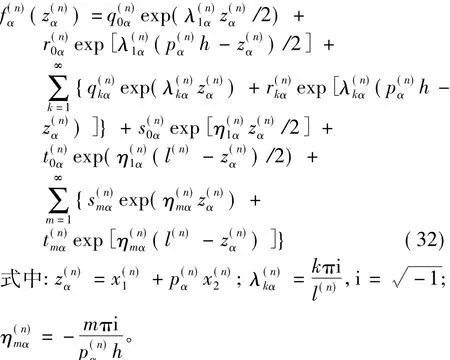
則根據式(27)～式(29)可以得到各部分彈性體的位移函數和應力函數，如位移函數可以表示為

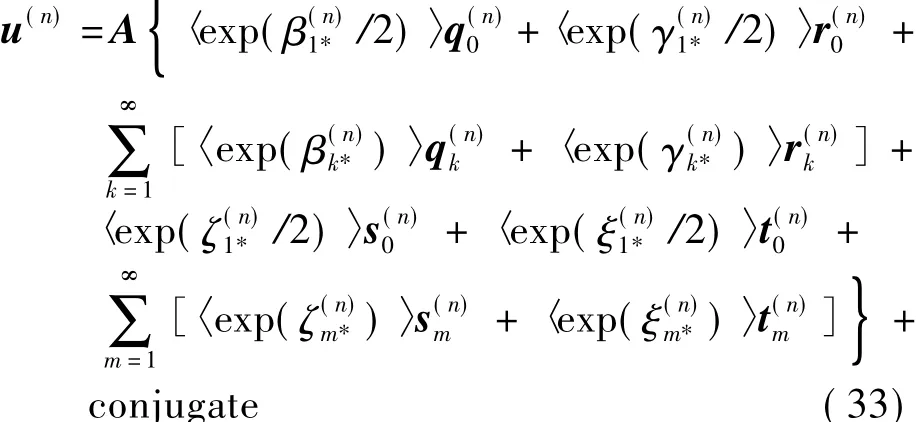
式中:

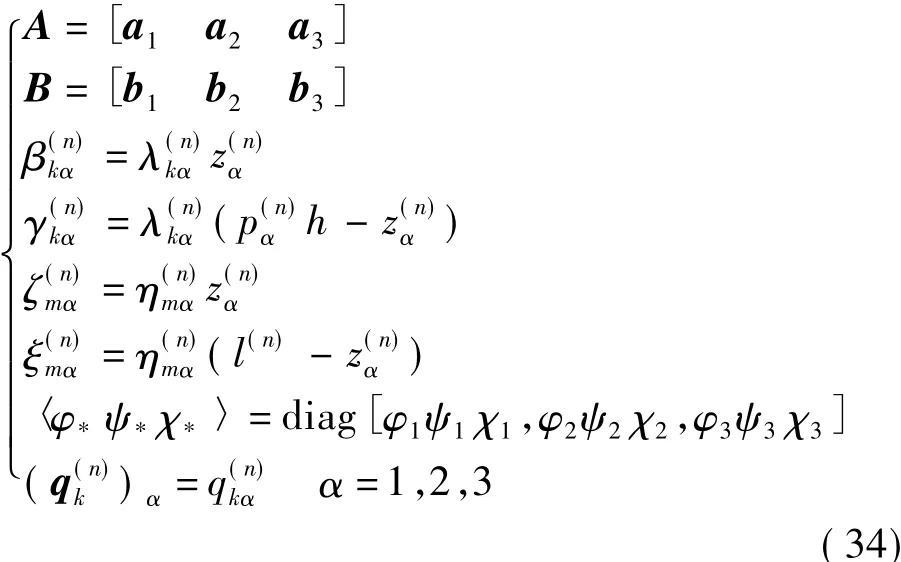
其中:、、都是3×1的列向量，其元素都為復數;conjugate表示式子中conjugate前面部分的共軛。

根據式(6)～式(9)給定的邊界條件，則有

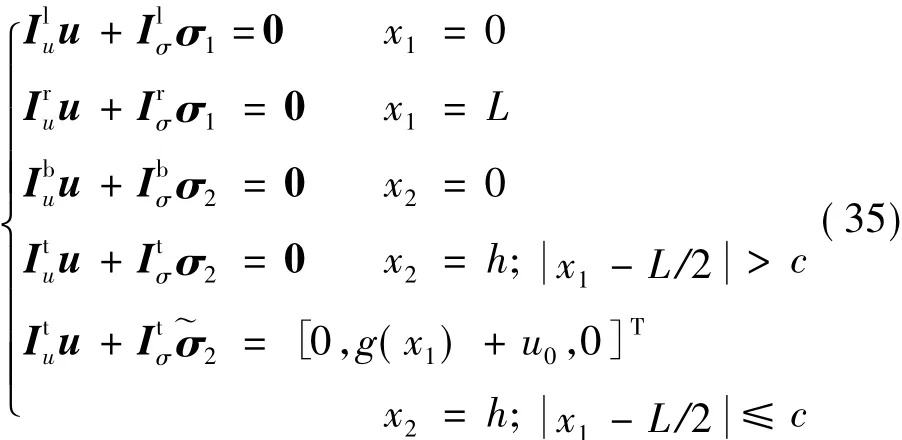
式中:、、和分別為彈性體上邊、下邊、左邊和右邊提取位移約束的3×3矩陣;、和分別為彈性體上邊、下邊、左邊和右邊提取應力約束的3×3矩陣。

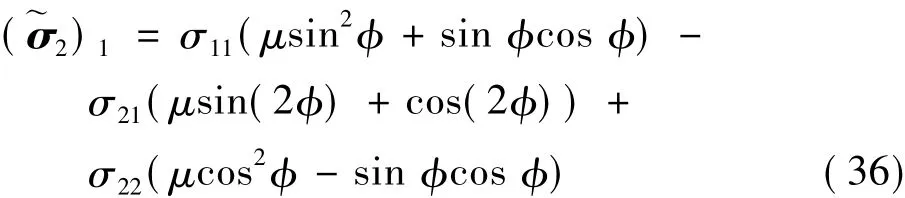
為了滿足式(35)的邊界條件和式(30)的連續性條件，采用傅里葉積分的方式來進行計算:

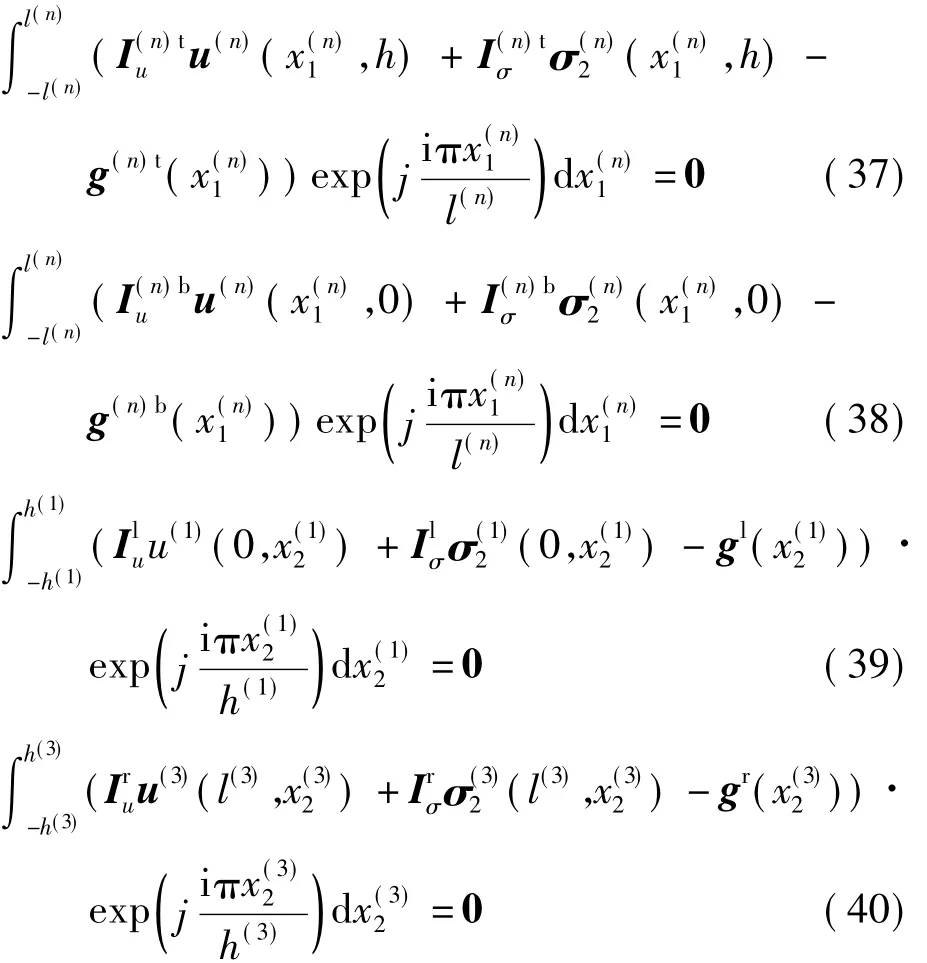
式中:j=0，1，2，…;n=1，2，3。

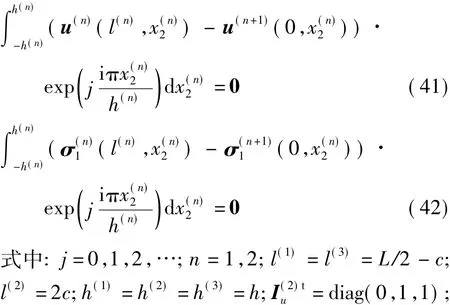
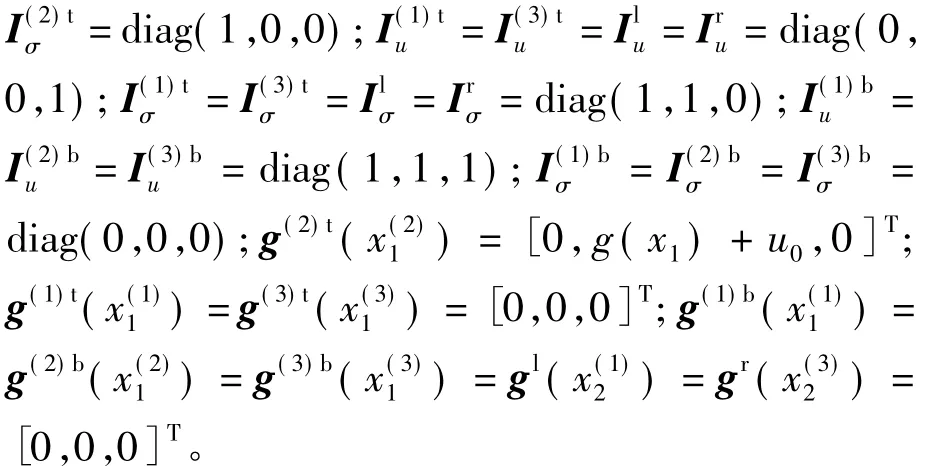
通常情況下，非接觸高度u0是未知量，可以通過求導的方式消去u0，區域Ⅱ頂部的邊界條件式可以轉化為

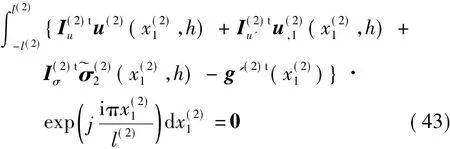
式中:

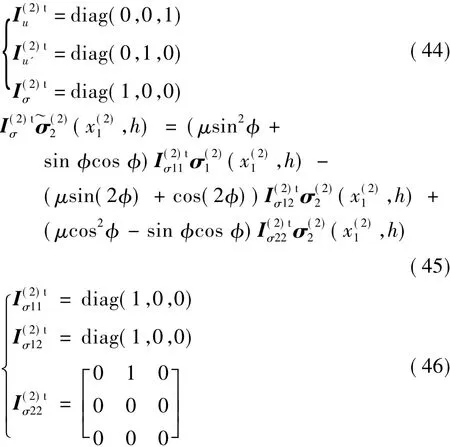
式(45)代入式(43)可得

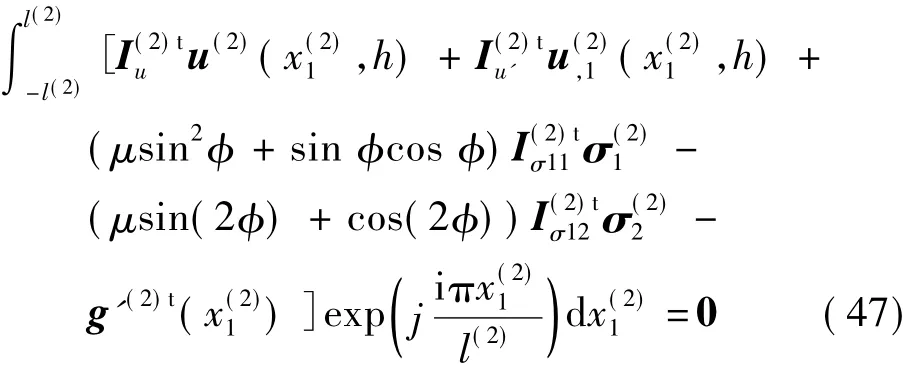
為了保證函數在各邊界、交接處的收斂效果相近，本文令各部分的k和m的上界滿足:

式中:Ceil(*)表示大于或等于*的最小整數;K為所有K(n)相加之和。根據k和m的取值，選取合適的j值可求解()函數中的各個參數，便可分別求得三部分彈性體的位移和應力函數表達式。在實際計算過程中，k和m的取值不可能無限大，且求解到的位移的收斂性要比應力的收斂性好。并且在區域Ⅰ與區域Ⅱ交接處和區域Ⅱ與區域Ⅲ交接處往往存在應力突變，同時，非接觸區域存在應力不近似于零的問題。這樣求解到的函數結果不能很好地吻合最初設定的邊界條件。為了解決這些問題，以下采取整體位移約束法和線性疊加原理，通過迭代方式獲取更匹配最初邊界條件的位移函數和應力函數。

2.2 整體位移約束法解決交接處應力突變問題

在劃分成三部分彈性體計算時，在x2方向上，區域Ⅰ和區域Ⅲ頂部給定的是應力約束條件σ22=0，而區域Ⅱ給定的是位移約束條件 u2=g(x1)+u0。可見彈性體頂部存在不同形式的約束，導致交接處存在應力突變問題。為此，將三部分彈性體再視為整體進行考慮，指定以下約束條件:

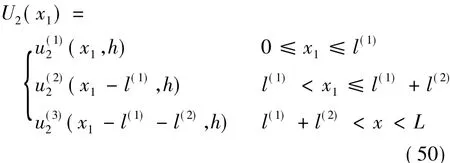
并假設

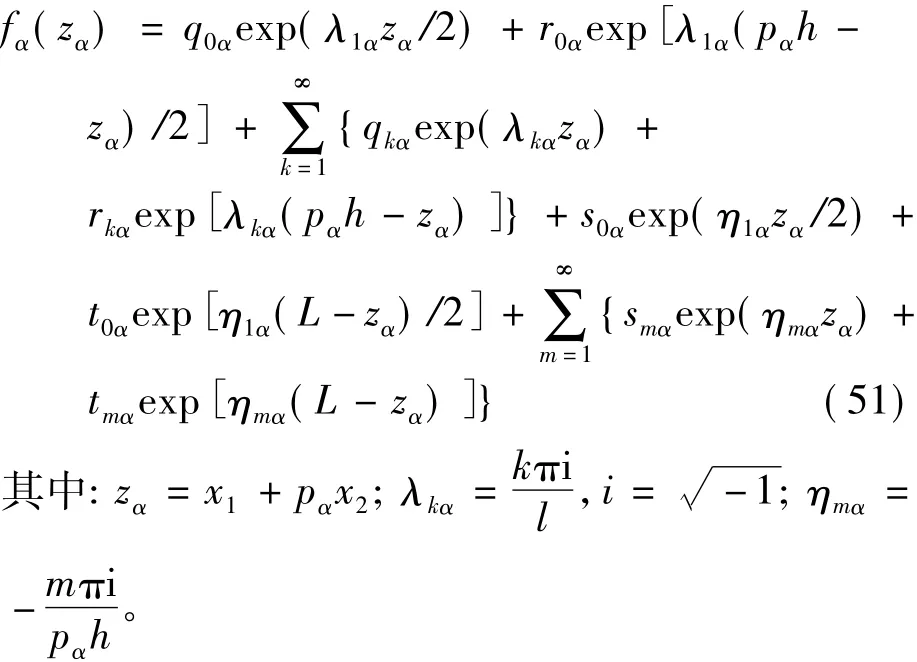
此時的邊界條件可以表示為

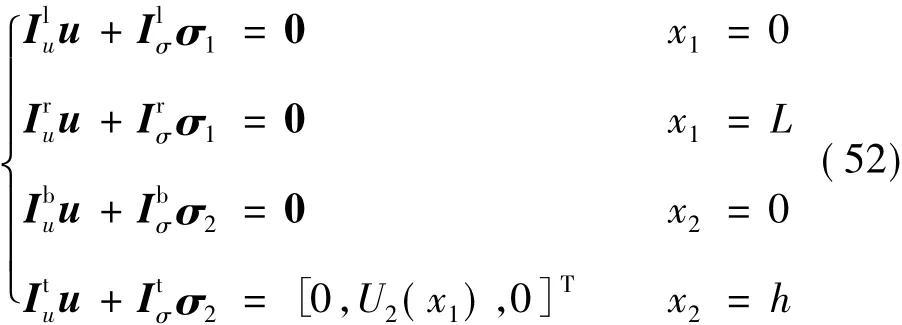
式中:

按照 2.1節中的傅里葉積分的方式對式(52)求解可以求解fα(zα)函數中的各個參數，便可求得彈性體的位移和應力函數表達式u、σ1、σ2。

2.3 線性疊加法解決非接觸區域應力不為零的問題

通過整體法得到位移和應力函數后，在非接觸區域仍然存在著正應力不近似于零的問題。此時分別提取區域Ⅰ和區域Ⅲ部分進行單獨分析:先通過整體位移約束法的應力函數計算得到彈性體區域Ⅰ和區域Ⅲ頂部的應力σ12和σ22，之后將得到的應力σ12和σ22取反后分別作為單獨計算時區域Ⅰ和區域Ⅲ頂部的應力約束;區域Ⅰ和區域Ⅲ底部固定，在x1、x2和x3方向上給定位移約束;對于區域Ⅰ和區域Ⅲ左右兩側，在x1和x2方向上給定應力約束，在x3方向上給定位移約束。因此，此時彈性體區域Ⅰ和區域Ⅲ位移、應力函數計算的邊界條件為

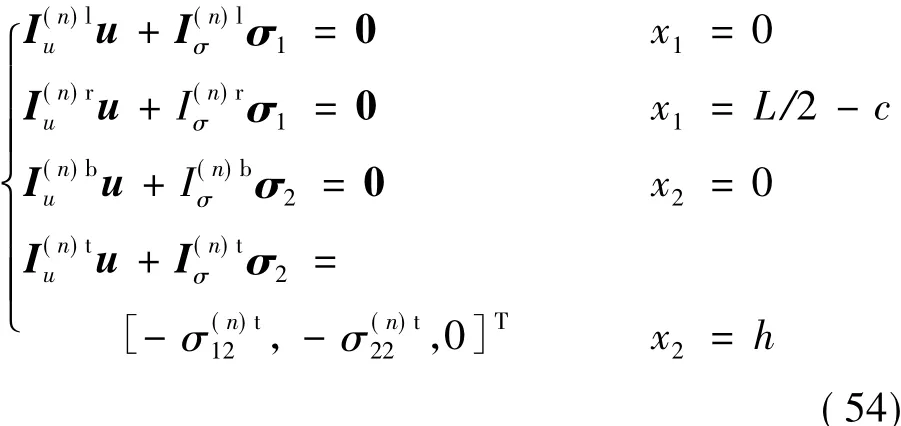
其中:n=1，3。

同樣依照前面的計算方式求解出()函數中的各個參數，得到⌒式(54)邊界條件下位移、應力的函數表達式為、。然后將其與之前整體位移約束法計算的結果、、行疊加，并將疊加的結果作為邊界條件的一部分進行再一次的整體計算，與2.2節中邊界條件相同，但是頂部位移約束條件的數值發生改變:

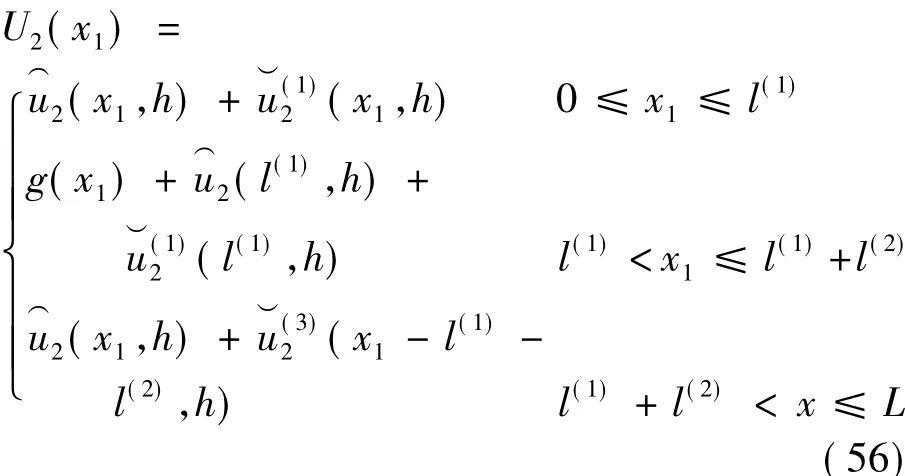
依據邊界條件和上述的位移約束條件函數求解出位移、應力表達式u、σ1和σ2。到此，便完成了線性疊加。

2.4 迭代法逼近理想解

通過2.2節中的整體位移約束法計算和2.3節中的線性疊加法計算，非接觸區域的應力在一定程度上變小，但還是不為零。由于應力函數給定的是傅里葉級數的函數形式，且k和m的取值有限，因此不能保證彈性體頂部非接觸區域每個點的應力滿足σ12=0和σ22=0，只能使其值近似于零。

對于σ12和σ22不近似于零時，需要將2.3節計算出來的u、σ1和σ2記為，然后重復2.3節中的線性疊加法，在區域Ⅰ和區域Ⅲ單獨計算出疊加后作為整體計算時的邊界條件，再次得到u、σ1和σ2。最后再次判斷是否σ12≈0和σ22≈0，若不滿足則再次重復上述操作，進行迭代。在計算出線性疊加后的位移函數和應力函數后，可通過每次迭代后對應力改變量是否小于一個值來判定迭代是否結束。

3 算法驗證

3.1 圓柱壓頭接觸問題驗證

為了驗證算法的正確性以及優越性，參考文獻［16］中的數據給定參數:

式中:E1、E2、E3分別為坐標軸3個方向的彈性模量;G23、G31、G12分別為坐標軸3個方向的剪切模量;ν23、ν31、ν12分別為坐標軸 3 個方向的泊松比。

將剛體壓頭的外廓修改成圓柱形，則外廓函數為

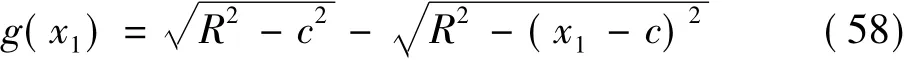
在MATLAB中編寫程序進行計算，再與文獻［14-15］的解析解(彈性半空間下的求解)做比較。圖2給出了K=500時頂部應力分布與文獻［14-15］彈性半空間法求解的應力分布。可以看到，在非接觸區域，當前解與彈性半空間解一致;在接觸區域，當前解也與彈性板空間解較吻合。圖3給出了K=500時接觸區域的相對誤差εre，進一步說明它的吻合程度。在圖3中，豎直2條虛線的中間區域代表了彈性體頂部

x1－L /2 ＜0.9c區域，在此區域內的最大相對誤差為2.6%。

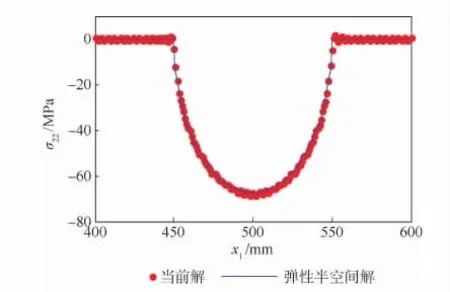
圖2 當前解與彈性半空間解的比較Fig.2 Comparison between present solution andsolution of elastic half space

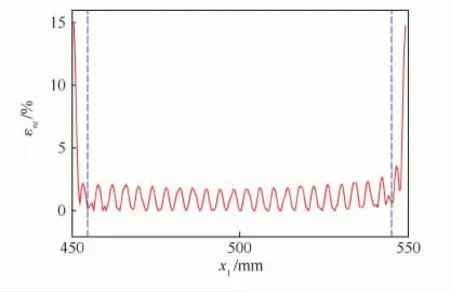
圖3 K=500時接觸區域應力的相對誤差Fig.3 Relative error of stress in contact zone at K=500

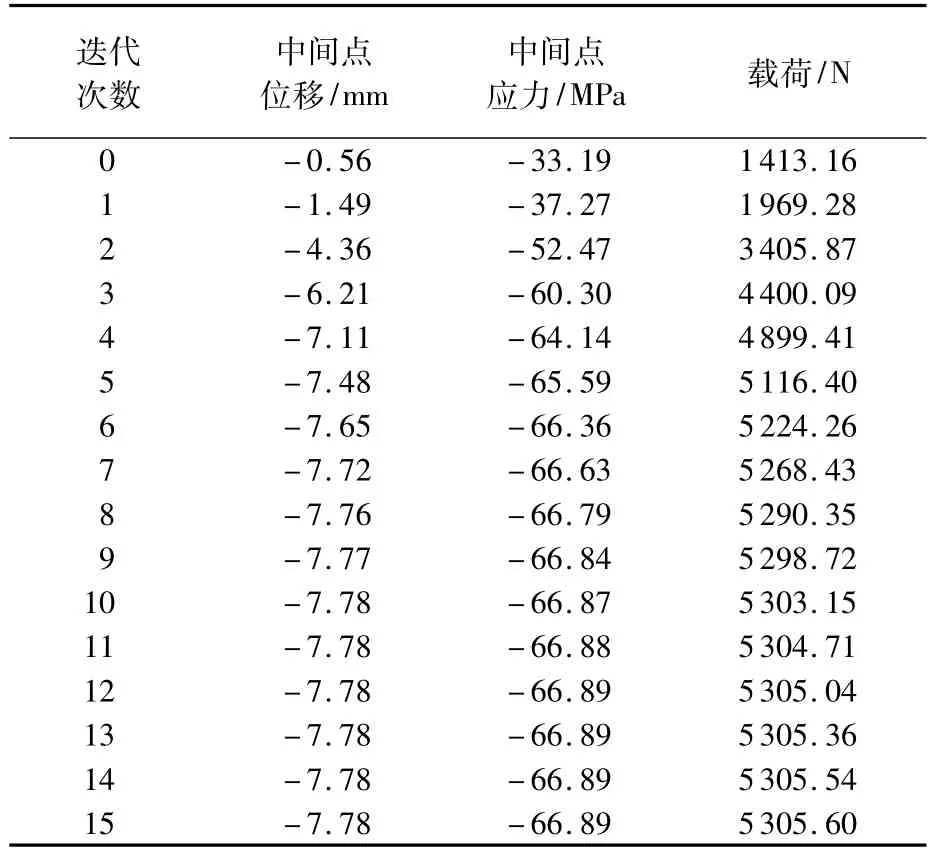
表1 K=400時的迭代結果Table 1 Iterative results at K=400

得到應力分布函數后，通過積分求得載荷值，表1為K取400時的迭代結果。隨著迭代次數增加，中間點的位移與應力、載荷的變化越來越小。經過15次迭代后載荷值為5305.60N。用文獻［14-15］的方法計算得到的載荷 Portho為5278.14 N，采用式(59)計算相對誤差，并與文獻［16］的計算結果進行比較。在文獻［16］的計算結果中，K=400時相對誤差為 1.9%，K=1000時相對誤差為0.8%，而本文在K=400時計算得到的相對誤差僅為0.52%。可見，本文計算結果的相對誤差更小，且在K取較小值時便能獲得較優的結果。

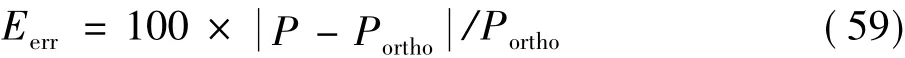
3.2 圓柱壓頭與有界彈性體接觸問題驗證

該求解方法與彈性半空間平面接觸問題求解不同，可以適用于求解有界彈性體的接觸問題。

給定參數如下:

取K=400，求解得到剛體壓頭的壓痕深度為4.788mm(實際收斂結果為4.78779mm)，載荷值為5 832.3 N。在ABAQUS軟件中依據上述的參數建立模型，由于ABAQUS中依據接觸寬度作為邊界條件比較困難，因此采用給定壓痕深度，反過來求接觸寬度。

在ABAQUS中給予剛體壓頭－4.788 mm的位移約束，仿真得到的接觸應力如圖4所示，求得接觸寬度為100.33 mm，載荷值為5 793.6 N。容易得到，計算的接觸寬度對于仿真結果的相對誤差為0.33%，計算得到的載荷值相對于仿真結果的相對誤差為0.67%。圖5顯示了彈性體接觸區域應力分布的計算結果和仿真結果，定義絕對誤差εab為計算值減仿真值，則最大絕對誤差為3.648 MPa;除去右邊靠近交接處的位置，其他位置的絕對誤差值都小于3 MPa。可見，本文求解方法在解決有界彈性體接觸問題上具有可行性。

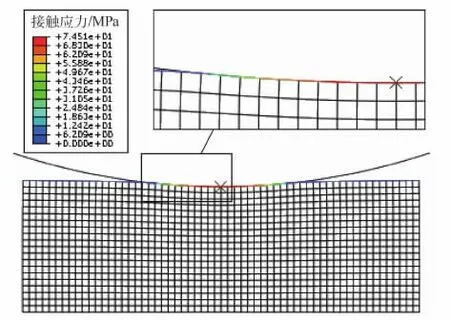
圖4 ABAQUS仿真接觸應力Fig.4 Contact stress of ABAQUS simulation

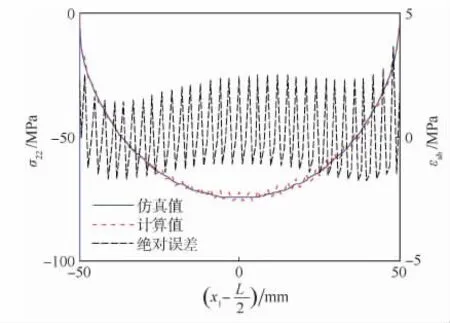
圖5 圓柱壓頭與有界彈性體接觸應力分布Fig.5 Distribution of contact stress between cylindrical indenter and bounded elastic body

3.3 倒圓角楔形壓頭接觸問題驗證

在圖1所示模型中，剛體壓頭是倒圓角的楔形，式(11)是它的外廓函數。該外廓函數對圓角半徑R=0時也適用。基于式(60)中彈性體的參數，給定楔形的參數:楔形斜度θ和圓角半徑R。在 θ取 10°時，R 分別取 0、50、100、150、200、250 mm進行計算，得到壓痕深度后作為位移約束在ABAQUS中進行對應的有限元仿真，得到表2、表3和圖6。

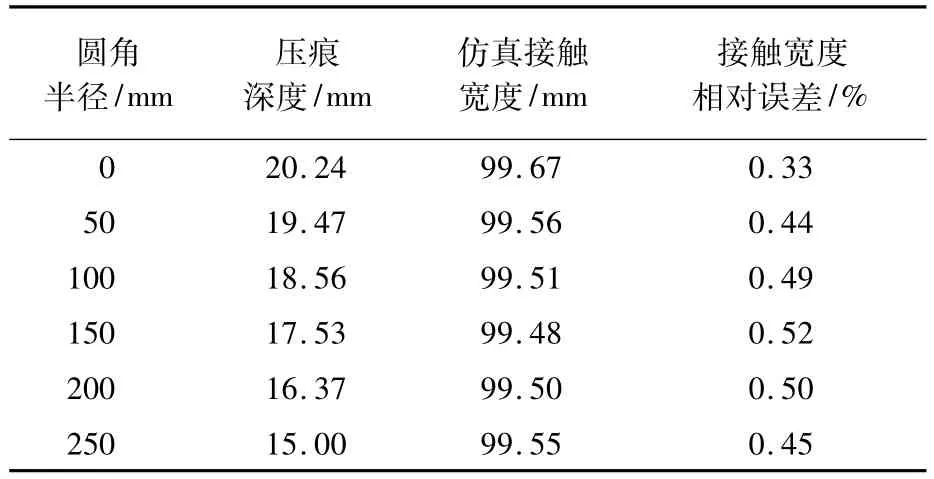
表2 不同R值下的壓痕深度與仿真接觸寬度Table 2 Indentation depth and simulation contact width at different R values

表2和表3表示在K=500時不同R值下的計算結果和仿真結果，并給出載荷值和接觸寬度的相對誤差。如表2所示，在有圓角的情況下，隨著R值的增加，達到相同的接觸寬度(2c=100 mm)，需要的壓痕深度值逐漸減少;如表3所示，隨著R值的增加，載荷值也逐漸減少。載荷值的相對誤差都小于2%，接觸寬度2c相對誤差都小于1%。可見，K=500時計算值和其對應的仿真值是比較接近的。

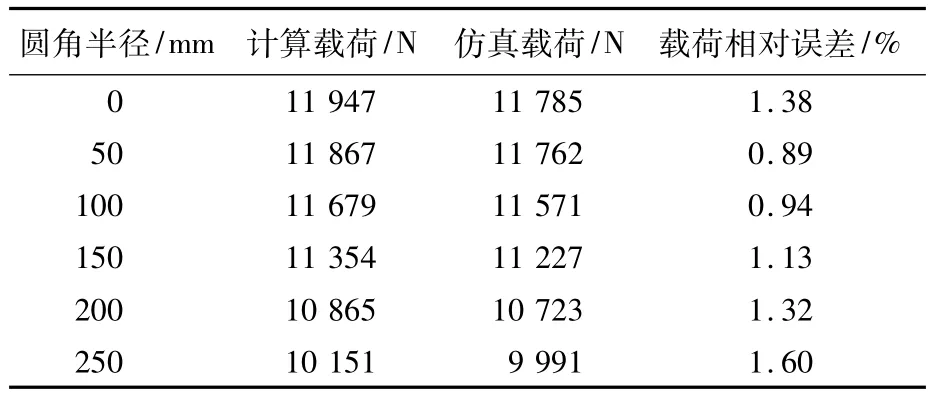
表3 不同R值下的計算載荷與仿真載荷Table 3 Calculation load and simulation load at different R values

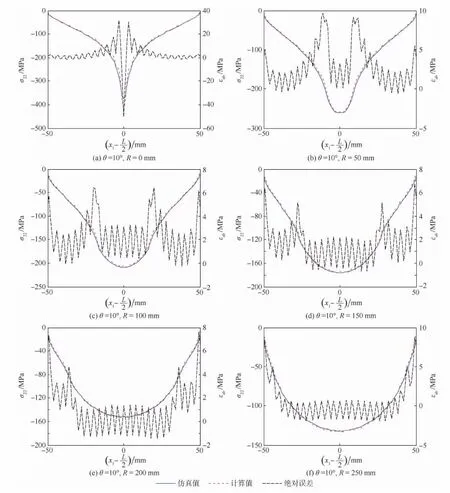
圖6 在θ=10°，R=0，50，100，150，200，250 mm時的計算與仿真應力分布及兩者的絕對誤差Fig.6 Computed and simulated stress distribution and absolute error between them at θ=10°and R=0，50，100，150，200，250 mm

圖6 為 R 取0、50、100、150、200、250mm 時計算得到的應力分布和仿真得到的接觸應力分布以及兩者的絕對誤差。在圖6(a)～圖6(f)中，坐標左右兩端的誤差比較大，一個原因在于左右兩端是接觸區域和非接觸區域的交接處，交接處的應力計算時不容易收斂且此處附近的點在x1軸方向上的位移變化相對中間區域的點要大。實際上，算法中給頂部的位移約束不是剛體壓頭的外廓函數減間隙高度，因為接觸點處不光發生了x2軸方向的位移，也在x1軸方向上也發生位移，因此實際給的外廓函數在x1軸方向上發生了形變。接觸區域各點在x1方向發生的移動指向接觸中心處，計算用的剛體壓頭相對于仿真用的剛體壓頭要略微“偏瘦”。另一個原因在于原本設定的級數函數就是為了逼近實際的位移函數和應力函數，求得的函數在理想的函數上就有一些波動。算法本身便會導致誤差，在斜率較大或突變的地方會更容易造成較大的誤差。

另外，在切點(圓弧和斜線的過度處)附近的絕對誤差值也要比正常地方的絕對誤差值大。例如，在 R=150 mm 時，Rsin 10°=26.04 mm，在圖6(d)中可以看出在x1－L/2=±26.04 mm附近絕對誤差值較大;在R=200 mm時，Rsin 10°=34.73 mm，在圖 6(e)中可以看出 x1－L/2=±34.73 mm附近絕對誤差也較大。因此，隨著R值的增加，絕對誤差較大處逐漸往外移動。

對于有圓角的楔形，從圖6(b)～圖6(f)可以看出，在接觸區域，計算值與仿真值的絕對誤差值小于10 MPa，除去交接點附近和切點附近，絕對誤差值小于5 MPa。

雖然接觸應力的絕對誤差并不小，但計算得到的應力函數在仿真得到的應力分布曲線上波動，由于誤差有正有負，能夠得到消除，使得最后得到的載荷值誤差較小。

4 結論

1)針對線性各向異性彈性體小變形接觸問題，本文基于Eshelby-Stroh公式，運用線性材料疊加原理和整體位移約束法，解決了圓柱型壓頭和倒圓角楔形壓頭與彈性體的接觸問題。

2)針對正交各向異性彈性體接觸問題，本文以圓柱壓頭為例，求得的結果在載荷值比文獻［16］求解結果更接近于文獻［14-15］的求解結果，且在K取較小值時便能算出相對誤差較小的載荷值:K=400時載荷計算值相對于文獻［14-15］彈性半空間計算結果的相對誤差為0.52%。本文算法更佳。

3)本文算法解決了圓柱壓頭與有界線性正交各向異性彈性體的接觸問題，并用ABAQUS仿真驗證:計算的接觸寬度和載荷對于仿真結果的相對誤差分別為0.33%、0.67%。

4)對于倒圓角楔形壓頭與線性正交各向異性彈性體小變形接觸問題，在接觸區域和非接觸區域交接處的絕對誤差相對普通接觸點較大。同時在剛體壓頭外廓上，圓弧和斜線過度處也會發生應力絕對誤差較大的現象，并隨著R值的增加，絕對誤差較大處逐漸往外移動。至于普通接觸點的接觸應力，計算值和仿真值比較接近。雖然某些地方接觸應力的絕對誤差并不小，但通過積分得到載荷值的相對誤差都小于2%。因此，已知倒圓角楔形壓頭與線性正交各向異性彈性體的接觸寬度，通過本算法求解壓頭的載荷是可行的。

［1］ T YR S J，LYYRA-LAITINEN T，NIINIM K M，et al.Estimation of the Young’s modulus of articular cartilage using an arthroscopic indentation instrument and ultrasonic measurement of tissue thickness［J］.Journal of Biomechanics，2001，34(2):251-256.

［2］ KORHONEN R K，SAARAKKALA S，TOYRAS J，et al.Experimental and numerical validation for the novel configuration of an arthroscopic indentation instrument［J］.Physics in Medicine ＆Biology，2003，48(11):1565-1576.

［3］ DIMITRIADIS E K，HORKAY F，MARESCA J，et al.Determination of elastic moduli of thin layers of soft material using the atomic force microscope［J］.Biophysical Journal，2002，82(5):2798-2810.

［4］ WANNINAYAKE I B，DASGUPTA P，SENEVIRATNE L D，et al.Air-float palpation probe for tissue abnormality identification during minimally invasive surgery［J］.IEEE Transactions on Biomedical Engineering，2013，60(10):2735-2744.

［5］郭淵，關志東，劉德博，等.復合材料靜壓痕與落錘沖擊初始損傷對比試驗［J］.北京航空航天大學學報，2009，35(8):1018-1021.GUO Y，GUANG Z D，LIU D B，et al.Comparison between quasi-static indentation testing and drop-weight impact testing on delamination on set damage［J］.Journal of Beijing University of Aeronautics and Astronautics，2009，35(8):1018-1021(in Chinese).

［6］ STOLZ M，GOTTARDI R，RAITERI R，et al.Early detection of aging cartilage and osteoarthritis in mice and patient samples using atomic force microscopy［J］.Nature Nanotechnology，2009，4(3):186-192.

［7］ LIAO Q，HUANG J，ZHU T，et al.A hybrid model to determine mechanical properties of soft polymers by nanoindentation［J］.Mechanics of Materials，2010，42(12):1043-1047.

［8］ MUSKHELISHVILI N I.Some basic problems of the mathematical theory of elasticity［J］.Mathematical Gazette，1953，48(365):351.

［9］ ENGLAND A H，SIH G C.Complex variable methods in elasticity［M］.London:Wiley-Interscience，1971:318.

［10］ GLADWELL G M L，ENGLAND A H.Orthogonal polynomial solutions to some mixed boundary-value problems in elasticity theory［J］.Quarterly Journal of Mechanics ＆ Applied Mathematics，1977，30(2):175-185.

［11］ OKUMURA M，HASEBE N，NAKAMURA T.Crack due to wedge-shaped punch with friction［J］.Journal of Engineering Mechanics，1990，116(10):2173-2185.

［12］ STROH A N.Dislocations and cracks in anisotropic elasticity［J］.Philosophical Magazine，1958，3(30):625-646.

［13］ STROH A N.Steady state problems in anisotropic elasticity［J］.Studies in Applied Mathematics，1962，41(1):77-103.

［14］ FAN C W，HWU C.Punch problems for an anisotropic elastic half-plane［J］.Journal of Applied Mechanics，1996，63(1):69-76.

［15］ HWU C，FAN C W.Sliding punches with or without friction along the surface of an anisotropic elastic half-plane［J］.Quarterly Journal of Mechanics ＆ Applied Mathematics，1998，51(1):159-177.

［16］ BATRA R C，JIANG W.Analytical solution of the contact problem of a rigid indenter and an anisotropic linear elastic layer［J］.International Journal of Solids and Structures，2008，45(22-23):5814-5830.

［17］ JIANG W，BATRA R C.Indentation of a laminated composite plate with an interlayer rectangular void［J］.Composites Science and Technology，2010，70(6):1023-1030.

［18］ VEL S S，BATRA R C.The generalized plane strain deformations of thick anisotropic composite laminated plates［J］.International Journal of Solids and Structures，2000，37(5):715-733.

［19］ TINGT C T.Anisotropic elasticity theory and applications［M］.Oxford:Oxford University Press，1996:134-142.