復合樁基明德林解(Mindlin)任意空間域四維積分及程序實現
曾朝杰
(上海同建強華建筑設計有限公司,上海 200072)
0 引 言
在上海及沿海地區,軟土地基大量分布,但表層土由于反復毛細作用導致固結硬化,往往形成硬殼層,對于一般多層或小高層房屋而言,這層土承載力足夠、但下臥層變形太大,為節約樁基投資,在上世紀80年代以上海工程界為代表推出沉降控制復合樁基[1-2],本質是將樁基作為減少沉降構件,充分利用硬殼層承載力形成樁土共同作用,1994年出版文獻[2]較早論述復合樁基計算理論并進入地方規范體系,1999年出版文獻[3]完善了沉降控制復合樁基系統化設計計算理論。
但是采用文獻[2]、文獻[3]計算方法及目前軟件編制水平,均要假定樁基承臺承載比例,進行布樁,反復試算,直到計算沉降滿足要求為止,工作量很大,為降低試算工作量,本文研究不布樁情況下,自動將樁力在半空間離散再進行四維積分的計算理論及配套程序[5],并廣泛應用于工程實踐[6-7]。
1 復合樁基的基本應力計算公式
復合樁基應力計算公式由布希涅斯克(Boussinesq,布氏解)及明德林(Mindlin,明氏解)應力基本公式推導而成。
1.1 布希涅斯克及明德林基本解公式
布氏豎向應力基本解:
(1)
明氏豎向應基本解:
(2)
式中:A2=[n2+(m-1)2],B2=[n2+(m+1)2],F2=n2+m2,n=r/Lm=z/L。
樁地基應力計算基本尺寸關系如圖1所示,其中,d為樁截面尺寸(樁徑或者斷面寬度),L為樁長,Z為計算點離半空間頂面(地表)的距離(深度),r為計算點離樁軸線的水平距離。
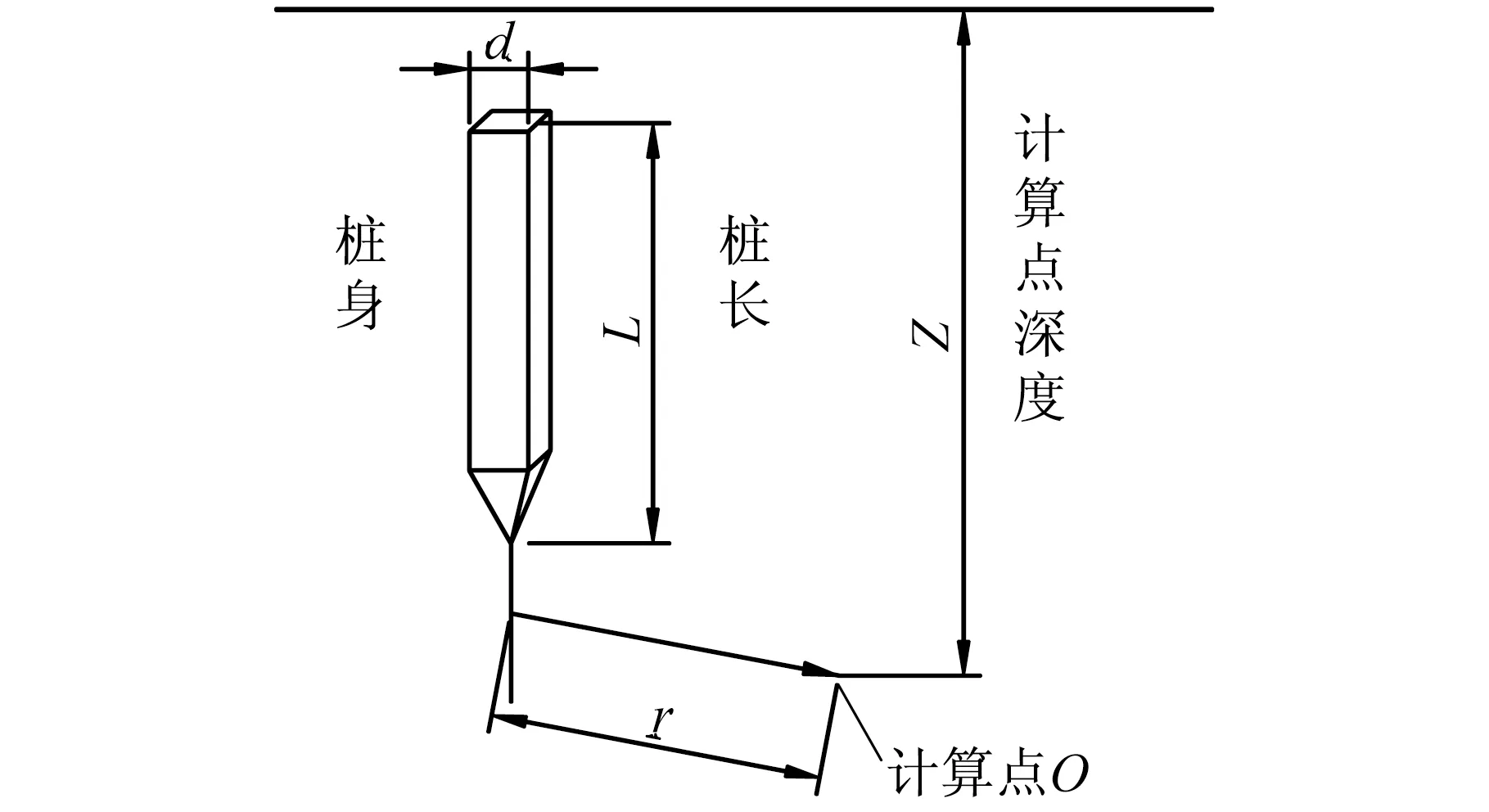
圖1 半空間明德林樁及尺寸示意圖Fig.1 Relevant size of a half space pile
1.2 可解析的積分解形式
對于上述基本解,只有在一些簡單平面域,如布氏解在平面矩形域、圓形域,明氏解在平面矩形域、圓形域、豎向均布、豎向線性增長(用于有樁地基)的情況下才能求得其解析積分解。
布氏矩形域角點應力積分解:
(3)
式中:m=L/b,n=z/L(L,b分別為矩形基礎長寬),并容易推導得文獻[3]中第4.3.1條中關于矩形中心沉降系數δ:
(4)
對于樁基應力計算則需要采用明德林-哥特斯(Mindlin-Geddes)積分解:
(1) 樁端集中力對地基的應力為前述基本解(參見式(2));
(2) 樁側摩阻力為矩形均布時對地基中的應力(式(5)):
(5)
(3) 樁側摩阻力為線性均勻增長時對地基中的應力(式(6)):
(6)
以上字母含義可參見圖1、圖2或文獻[3-4]。

圖2 單樁工作狀態下樁頂力的分解Fig.2 Decomposition of the pile top force
圖2中Q為樁頂集中力,αQ為樁尖集中力,βQ為樁側均布(線性平均)側阻力,(1-α-β)Q為樁側線性增長側阻力。
1.3 任意多連通域積分的數值解
在大多數情況下碰到的基礎形式均為不規則,那么求解不規則任意多連同域基礎下的土體應力,就只能以數值積分的方式進行,本文利用計算機圖形學、向量學計算技術,將這種無法解析的域剖分為多個可解析或較易積分的簡單域—三角形平面域及三角形棱柱體空間域,然后進行高精度辛普生變步長數值積分即可求得地基任意點應力。
2 復合樁基沉降計算基本方法及原理
本文一切計算均嚴格按照文獻[3-4]的規定,但在計算技術上利用了數學、測量學及計算機圖形學上知識,在嚴謹性、科學性、適應性方面有其獨特優點,同時能充分體現文獻[3-4]在復合樁基計算方面特點;在此,將文獻[3-4]中沉降計算原理作一簡述。
2.1 天然地基
天然地基的沉降計算按分層總和法進行計算,文獻[3]第4.3.1條:
(7)
地基壓縮層從基底算起,至應力比0.1為止(應力比方法,若為變形比方法也很容易實現),計算點取為基礎形心,計算結果為基礎平均沉降。
2.2 沉降控制復合樁基
在常規樁基的設計中,外荷載完全由樁基承擔,這時樁數較多,工程造價很高。在滿足安全的前提下,采用樁土共同作用計算的方法,即本文及文獻所述沉降控制復合樁基。
它是一種介于淺基與常規樁基之間的一種過渡基礎類型,沉降計算時,它假定:當作用于承臺底面的荷載準永久值效應組合值P大于各單樁極限承載力標準值之和時,樁分擔相當于各單樁極限承載力標準值之和的荷載、承臺地基土分擔其余荷載;反之,樁承擔全部荷載。具體計算時按下列原則進行:
(1) 當P-σCAC>kRk時,復合樁基沉降由兩部分構成,一部分由樁頂附加荷載Rk+Gpk的k根樁作用下產生的沉降,按文獻[3]第6.4.2條計算,但沉降經驗系數宜取1.0;另一部分由承臺底面附加荷載P-σCAC-kRk產生的沉降,計算同天然地基;
(2) 當P-σCAC≤kRk時,復合樁基沉降由樁頂附加荷載(P-σCAC)/k+Gpk的k根樁作用下產生的沉降,按文獻[3]第6.4.2條計算,但沉降經驗系數宜取1.0。
上述P為上部結構在基底產生的附加荷載,σC為承臺地面承擔的應力,AC為承臺面積,k為樁數,Rk為單樁極限承載力標準值。單樁極限承載力為土對樁的極限支承力及材料強度雙控,計算時按文獻[2-3]要求宜取0.8折減系數,計算點一般取為群樁形心。
2.3 沉降計算公式
由上述方法,就可以求出地基中應力σ,在求解平面上任意一點(x,y)的沉降時,沉降可表示為
第i層土應力面積積分:
(8)
第i層土分層沉降:
(9)
基礎總沉降:
S=ψΣSi
(10)
式中:hi-1為基礎底面(或樁尖平面)到第i層土的頂面距離;hI為基礎底面(或樁尖平面)到第i層土的底面距離;Ωx,Ωy分別表示多個任意平面形狀多連通域基礎形成的積分域,本文中用分段折線來模擬該域,并在積分時用分段函數來表示積分上下限;ψ為經驗調整系數,由規范或有經驗的專家確定,與地域或計算應力方式有關。
3 復合樁基明德林解(Mindlin)任意空間域積分的計算原理
通常,為按照前述原理進行復合樁基的沉降計算,必須先假定承臺的分攤比例,再進行樁數的假定計算,然后按照假定樁數進行布樁,樁數布好之后,進行計算,計算沉降過小,再進行減樁,沉降太大,就進行加樁,要反復進行多輪次計算,最終達到理想樁數,作為最終確定的復合樁基設計方案。
本文利用了求積儀原理,任何空間域都可以先從平面域著手,平面域的積分完成,再利用明德林-哥特斯解沿深度方向進行一次線性積分就可以完成整個四維空間積分。
具體的做法事,將平面不規則的單連通域、多連通域近似看做折線逼近,如圖3所示,所有連通域都可以剖分成三角形簡單域,由沉降計算點(一般是樁基的形心點)引出線與各轉折點相連,如轉折點數字是n的話,則形成了n三角形域(如圖3所示,五個角點即形成5個三角形)。
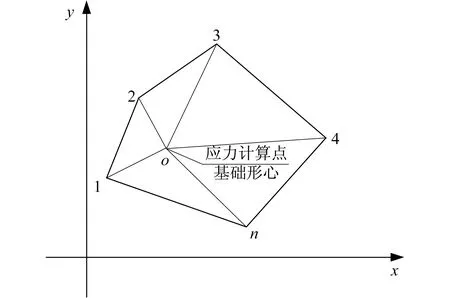
圖3 連通域的三角形剖分 Fig.3 Triangulation of connected domains
在做數值積分時,每一個三角形均可按照式(12)、式(13)進行分段積分,一般可以分成兩段,積分采用的是高精度變步長辛普生積分[8],平面域可以解決布希涅斯克及明德林樁尖面力的積分解,再沿著深度方向積分就完成了明德林樁側力(視作體積力)的第四維積分。
對于圖3中的三角形域△O34為例,可以進一步劃分為圖4所示積分域1(△O3d)及積分域2(△34d),再進行分段積分即可,則地基深度標高Z處的附加應力為
σz=σ1+σ2
(11)
式中:σ1,σ2用如下積分上下限函數表示。
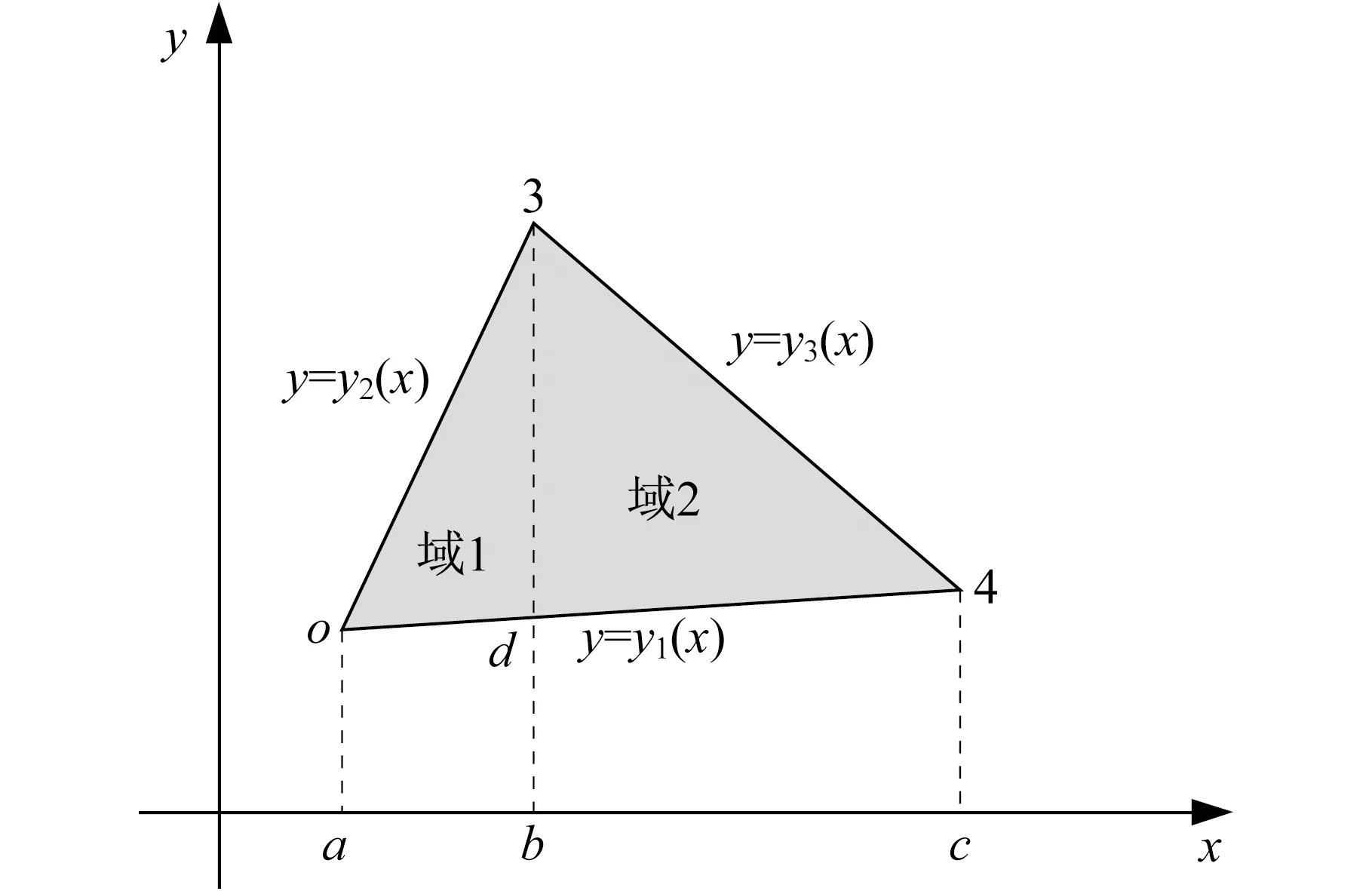
圖4 三角形域的數值積分及上下限Fig.4 Numerical integration upper and lower bounds of triangular domain
積分域1的豎向應力:
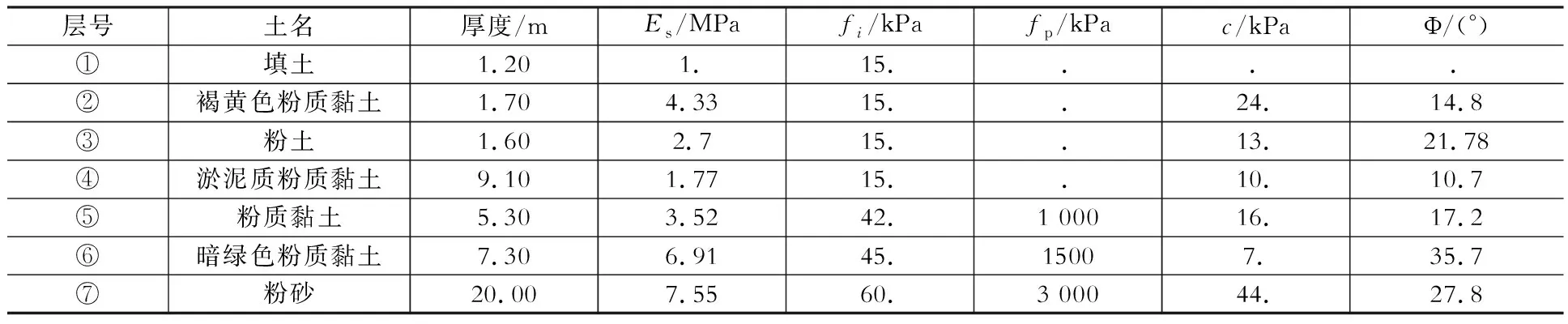
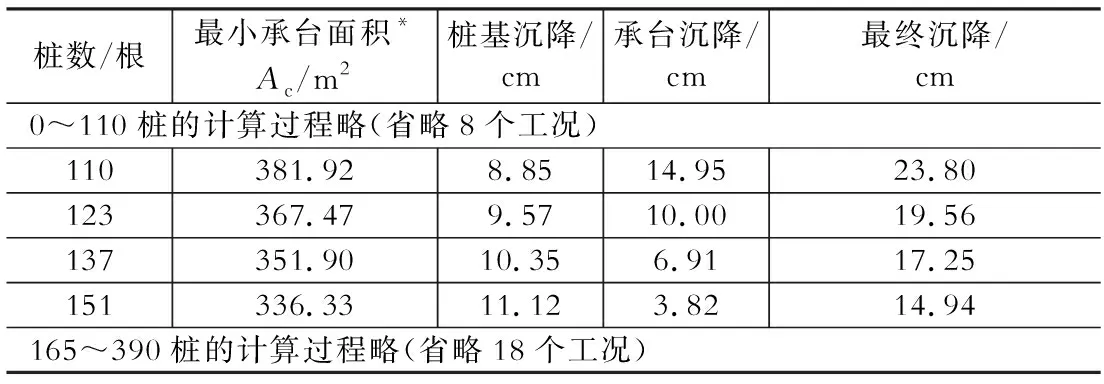
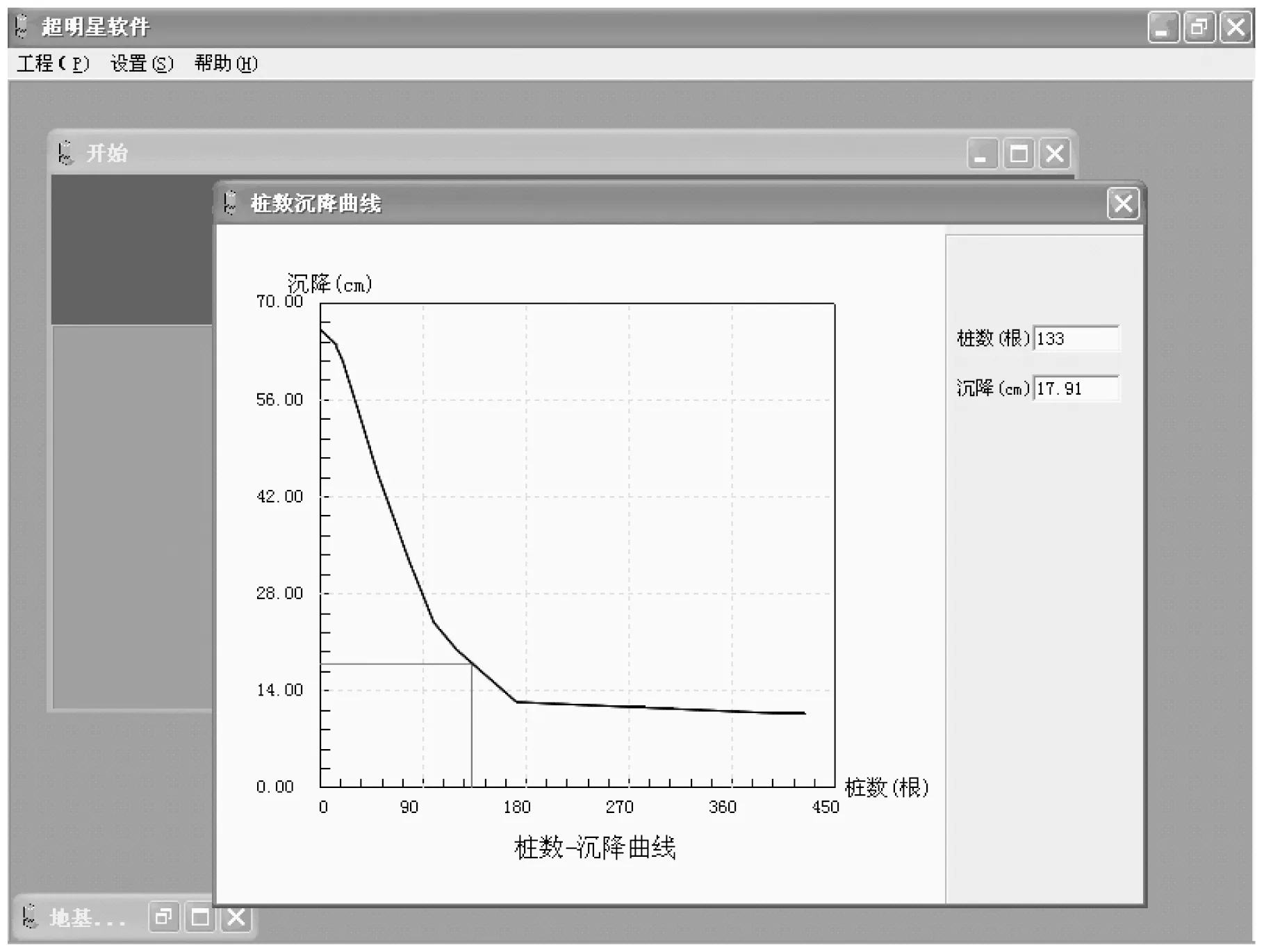
當a (12) 積分域2的豎向應力: 當b (13) 由圖4及式(12)、式(13)可見,積分域上下限都是可解析線性函數,數學表達簡單,配合數值積分則容易編程實現。 根據以上先離散再積分數值計算原理,本文編制了相應Fortran程序,并配置了人機交互友好界面成為《超明星地基強度與沉降計算軟件》,參見文獻[5],該軟件經上海市科學技術委員會鑒定為國際先進水平,后又評為規范配套軟件,成為很多巖土工程科研部門在方案階段咨詢、研究的基本工具。 針對文獻[3]規范編制組給出的例題(考題,參見圖5),按照133根樁最終施工圖的計算結果,同時利用本文編制的軟件計算,軟件生成計算結果及簡要過程如下: 圖5 規范例題(樁位及基礎平面簡圖)Fig.5 TheSpecification example (Foundation plan) 由文獻[3]式4.2.3-1并結合表1所示地質報告參數,最終求得地基承載力設計值fdh:fd=γdfdh=123.16 kPa。 本工程采用C30級,0.2 m×0.2 m×16 m混凝土預制方樁,單樁豎向承載力設計值:Rd=Rsk/γs+Rpk/γp=194.42 kN (土體承載力控制)。 表1工程地質地層參數簡表 Table 1 Engineering geological formation parameters 5.3.1工程概況 本工程為6層樓磚混結構住宅,采用沉降控制復合樁基,上部結構荷載設計值Fd=54 000 kN,上部結構荷載準永久值效應組合值為43 500 kN。承臺埋深1.27 m,地下水位-0.5 m,承臺總面積Ac=355.72 m2;樁長為16 m,樁截面邊長(樁徑)為0.2 m,按樁基承載計算所需樁數為399根。 5.3.2沉降控制復合樁基樁數-沉降曲線 根據文獻[3-4]要求,為確定有效控制沉降樁數,軟件自動計算樁數沉降(表2),自動生成樁數沉降曲線(圖6)。 表2計算成果一覽表 Table 2 Calculation results list *注:承臺面積AC系指滿足復合樁基承載力要求的最小承臺面積,程序默認共計算30種樁數-沉降工況,為節約篇幅省略掉自動生成的工況26個;樁數為133根時,軟件自動內插計算得沉降為17.91 cm作為計算成果(布好樁以后可再進行復核對比,參見圖6) 圖6 軟件自動生成樁數沉降曲線Fig.6 Pile number vs.settlement curve by software 按照文獻[3-4]算法以及本文提供的數值積分算法,對比如表3所示。 表3計算成果對比表 Table 3 Calculation results comparison list 備注:①準確解指布好樁后,嚴格按照規范方法應力疊加計算所得;②規范計算解指按照規范,采用同心圓方法歸并,查表簡化計算得到的求解,參見文獻[3]。 根據表3對比可見,本文方法與規范準確解偏大約2.6%,在工程設計計算合理偏差范圍內。 本文方法及配套軟件[5]實現了:①自動將基底力、樁力離散為面力和半空間體積力;②自動剖分平面多連通域為三角形域、剖分空間域為三角棱柱域;③自動完成面力及半空間體積力在地基應力中的積分;④自動根據變形控制要求進行多工況計算及插值,確定承臺面積及樁數。 根據算例及對比可見,本文提供算法及相應程序,在計算準確度上已足夠在復合樁基方案階段估算之用,無須布樁應力離散并積分方式得出的計算結果,與準確解、規范法差異均在3%左右,而大大提高計算效率,使得原來需要數天時間計算才能確定復合樁基方案,僅需數分鐘就可完成,本程序實現的軟件已經在工程界大量投入使用。4 程序實現
5 算例對比
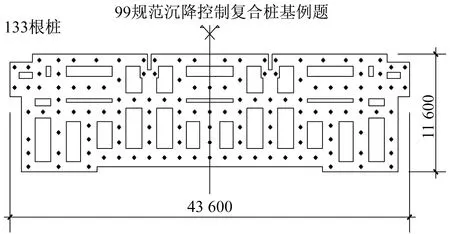
5.1 天然地基承載力設計值計算(過程略)
5.2 單樁豎向承載力設計值計算(過程略)
5.3 沉降控制復合樁基樁數-沉降曲線計算
5.4 計算成果對比

6 結 論

