黏滯阻尼器減震結構地震響應分析方法研究

賈傳果 周 越 胡鵬飛

(1.山地城鎮建設與新技術教育部重點實驗室(重慶大學),重慶 400045; 2.重慶大學土木工程學院,重慶 400045)

0 引 言

結構耗能減震是通過在結構中設置耗能阻尼器,耗散輸入結構的地震能量,從而減小結構的振動反應,減輕結構的損傷。合理的減震設計,可使強震作用下主體結構基本保持線彈性工作狀態,而非線性狀態主要集中在局部布置的若干耗能減震裝置上,形成了典型的局部非線性問題[1]。耗能減震裝置從其工作機理上可分為位移型阻尼器和速度型阻尼器[2]。本文研究主要針對速度型阻尼器,如黏滯阻尼器。

對于非線性黏滯阻尼器,其阻尼力模型一般表示為F=sgn(v)C·|v|α的形式[3](sgn(·)為符號函數,C為阻尼系數,α為阻尼指數),其中阻尼指數取值范圍通常為0.1～1.0[4]。非線性阻尼器的優點在于其可以避免由于速度過大而導致的阻尼器超載現象,但較線性黏滯阻尼器,整體結構地震響應分析變得更為復雜[5]。

有文獻[6]提出簡化方法,通過估計非線性粘滯阻尼器的等效阻尼比,進行整體結構的地震響應分析。文獻[7]基于估計的等效阻尼比計算阻尼減震因子,該方法已被寫入FEMA450。這種方法給出的等效阻尼比與阻尼器的最大位移相關,故整體結構的地震響應分析仍需要迭代。事實上,等效阻尼比大多根據非線性阻尼器和線性阻尼器的能量消耗相等的原則確定的[8]。文獻[9]通過數值模擬比較了模態阻尼法、半功率點法等規范以外計算等效阻尼比的方法。但文獻[10]指出在阻尼比相同的條件下線性阻尼器減震結構與非線性阻尼器減震結構的地震響應有明顯區別,這在一定程度上也說明采用等效阻尼比進行非線性阻尼器減震結構的地震響應分析存在一定的誤差。

要提高精度,有必要對所得的局部非線性運動方法進行直接積分。傳統的顯式積分方法主要是針對非線性恢復力而言的[11]。對于安裝有阻尼器的結構,非線性阻尼使得原本顯式的積分方法不再是顯式的,故求解時仍需迭代求解[12]。而對于隱式積分方法,非線性阻尼力需要更多的迭代步數,增加了計算量。對于非線性黏滯阻尼器,上述常規的顯式或隱式積分方法可能出現嚴重的數值脈沖現象,從而導致時域分析方法的失穩現象[13]。

為避免迭代和提高計算穩定性,本文采用具有線性隱式特性的Rosenbrock積分方法。該方法主要有兩個特點:一是需要計算每個積分步起始時刻的Jacobian矩陣;二是每個積分步均存在逆矩陣求解過程。這兩個特點也是影響其計算量大小的關鍵因素。為此,本文對黏滯阻尼器的非線性數學模型進行線性化處理,并通過引入阻尼器方位矩陣,得到阻尼器減震結構的線性化運動方程。為進一步提高計算效率,本文在每一步積分過程中引入Sherman-Morrison求逆定理[13]簡化逆矩陣求解過程。本文還對每個積分步的放大矩陣進行了譜分析,驗證了該方法在求解非線性阻尼問題方面的穩定性。最終本文通過編制Matlab有限元程序對7層黏滯阻尼器減震結構進行地震響應分析,驗證了該方法的計算效率和可靠性。

1 Rosenbrock積分方法簡介

Rosenbrock積分方法是在隱式Runge-Kutta方法[14]基礎上,采用內嵌牛頓迭代法實現顯式化,被稱為線性隱式方法[15],常用于一階剛性系統初值問題的求解。Rosenbrock方法保持了Runge-Kutta方法的穩定性,同時避免了迭代。對于一階非線性常微分方程,其初值問題可寫為

(1)

將總計算時間等分為N個長度為△t的時間步長,記tk=k△t,yk為tk時刻的狀態變量,應用二階Rosenbrock法(2-stage L-stable Real Time Compatible method即LSRT2方法)[16]得出tk+1時刻的狀態變量為

yk+1=yk+k2,

(2)

k1=(I-γΔtJ)-1f(yk,tk)Δt

(3)

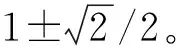
對于安裝有阻尼器的結構,可以假定結構的恢復力為線性,阻尼力為非線性,其運動方程為

Ma(t)+C0v(t)+FD(v(t))+Kd(t)=P(t)

(4)

式中:M為質量矩陣;C0為結構固有阻尼矩陣;FD為非線性阻尼力向量;K為剛度矩陣;d為位移向量;v為速度向量;a為加速度向量;P為外界激勵。

為采用LSRT2法,將二階動力方程式(4)轉化為一階形式:

(5)

通過對無阻尼自由振動的分析計算,文獻[9]對LSRT2方法進行了譜分析,給出了LSRT2法、Generalized-α法和Chang法的譜曲線對比圖(圖1),其中,ρ為普半徑,Ω為數值頻率(Ω=ωΔt)。由圖1看出,LSRT2方法在整個Ω的取值范圍內均小于等于1,高頻區間(Nyquist frequency右側)ρ隨Ω的增大逐步趨近于0,低頻區間(Nyquist frequency左側)ρ隨Ω的減小逐步趨近于1,說明LSRT2方法具備高頻過濾特性,且能保證低頻響應精度。文獻[18]證明了Rosenbrock方法是能量衰減或保守的算法,這樣的特性有利于其非線性穩定性[19]。

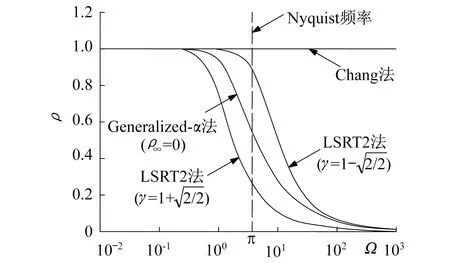
圖1 LSRT2法的ρ-Ω關系曲線Fig.1 ρ-Ω curves of LSRT2 method

2 阻尼力模型線性化處理

為表述方便,假設阻尼指數為既約分數,即α=q/p,且q和p均為奇數,則阻尼力公式轉化為F=C·vα。采用LSRT2法求解非線性問題時,每步均需求解當前步初始時刻的Jacobian矩陣。為簡化積分過程,首先對阻尼力在tk時刻進行線性化處理,即對阻尼力在tk時刻按泰勒級數展開,并僅取線性項:

(6)

式中:vk為阻尼器tk時刻的相對位移。

令線性化后的阻尼系數為

(7)

則式(6)的阻尼力方程可以簡化為

(8)

3 建立線性化運動方程

以平面框架模型為例,假設有m個自由節點,其位移和速度向量可表示為

d={x1,y1,β1,x2,…,xi,yi,βi,…,xm,ym,βm}

(9)

(10)

式中:xi,yi,βi為第i個結點的水平位移、豎向位移和轉角位移。

假設有n個阻尼器,且均與結構在結點處鉸接,其中第i個阻尼器的阻尼參數分別為Ci和αi,其與水平方向的夾角為θi。現引入阻尼器方位向量Li。如果阻尼器i一端與地面相連,一端與結點j相連,列向量Li的第3j-2個元素為cos(θi),第3j-1個元素為sin(θi),其余元素均為0,即

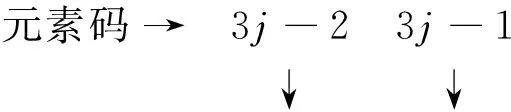
Li={0,…,cos(θi),sin(θi),0,…}T

文中所有上標T均表示矩陣或向量的轉置。

如果阻尼器i一端與結點j相連,一端與結點k相連,那么列向量Li的第3j-2個元素為cos(θi),第3j-1個元素為sin(θi),第3k-2個元素為-cos(θi),第3k-1個元素為-sin(θi),其余元素為0,即

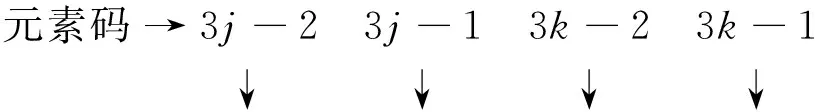
Li={…,cos(θi),sin(θi),…,

-cos(θi),-sin(θi),…}T

阻尼器i的軸向相對速度則可表示為

(11)

按公式(7)可得到阻尼器i的阻尼參數

(12)

式中:v(tk)為tk時刻的速度向量,后簡寫為vk。

按公式(8),可得到阻尼器i的附加阻尼力為

(13)

結構上阻尼器產生的阻尼力向量可以表示為

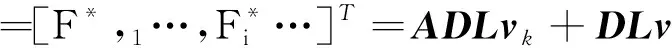
(14)

式中:A和D均為對角矩陣,

L矩陣是由每個阻尼器的方位列向量組成方位矩陣的轉置,即

L={L1,L2,…,Li,…Ln}T

阻尼力向量左乘L矩陣的轉置可得到所有節點所承受的阻尼力向量,

FD=LTF*=LTADLvk+LTDLv=

LTALPLTDLvk+LTDLv

(15)

式中:LP為矩陣LT的偽逆矩陣[12],若令W=LTALP,Ca=LTDL,式(15)可簡化為

FD=WCavk+Cav

(16)

再代入結構運動方程(4)可得

Ma+(Ca+C0)v+Kd=P-WCavk

(17)

因此,對于一個含有相同類型阻尼器(阻尼系數C和阻尼指數α均相同)的結構,其運動方程就可以寫為

(18)

4 改進Rosenbrock積分方法

對于線性化后的運動微分方程式(17),轉化成一階方程即為

(19)

其中,

應用LSRT2求解常微分方程式(17),則式(2)和式(3)的k1和k2可以表示為

(20)

k2=[I-γΔtJ]-1

(21)

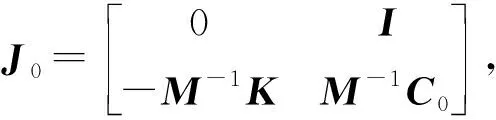
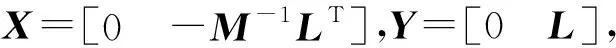
在式(20)和式(21)中存在矩陣求逆的過程。這是影響整個積分過程計算效率的關鍵。根據Sherman-Morrison定理[12],其中的逆矩陣求解可轉化為

G=[I-γΔtJ]-1=[I-γΔtJ0-γΔtXDYT]-1=

H-γΔtHXBYTH

(22)

其中,H=[I-γΔtJ0]-1,B=[D-1-γΔtYTAX]-1。H矩陣可以在積分之前計算。因此,每個積分步中矩陣求逆只是計算B矩陣。B矩陣的維數與阻尼器的個數n相等。而G矩陣的維數與有限元的節點相關,大致為6m。一般情況下,阻尼器是局部布置的,故m?n。原有Rosenbrock積分方法需要對一個6m維的矩陣求逆,而本文考慮Sherman-Morrison求逆定理后,只需要對一個n維矩陣求逆,理論上計算量得以大幅降低。

此外,由于非線性阻尼力模型的存在,原有Rosenbrock積分方法需要三次進行冪函數計算,即Jacobian矩陣更新、起點時刻f(yk,tk)和中點時刻f(yk+1/2,tk+1/2)計算。統一對線性化后的方程(17)進行積分,只需要一次冪函數計算,這也在一定程度上提高了計算效率。

5 穩定性分析

文獻[17]對LSRT2方法求解無阻尼系統的穩定性進行了譜分析。改進的LSRT2方法每一步積分過程都是針對一個線性方程,但在線性化后運動方程的右邊有一個項與初始時刻的速度相關。因此,本文采用譜分析方法對帶有非線性阻尼力模型的單自由度系統進行分析。假設單自由度系統質量m=1 kg;剛度k=1 N/m;結構固有阻尼系數c0=0。圖2和圖3給出了當附加阻尼器的阻尼系數為0.1,不同阻尼指數對應的ρ-Ω關系曲線。

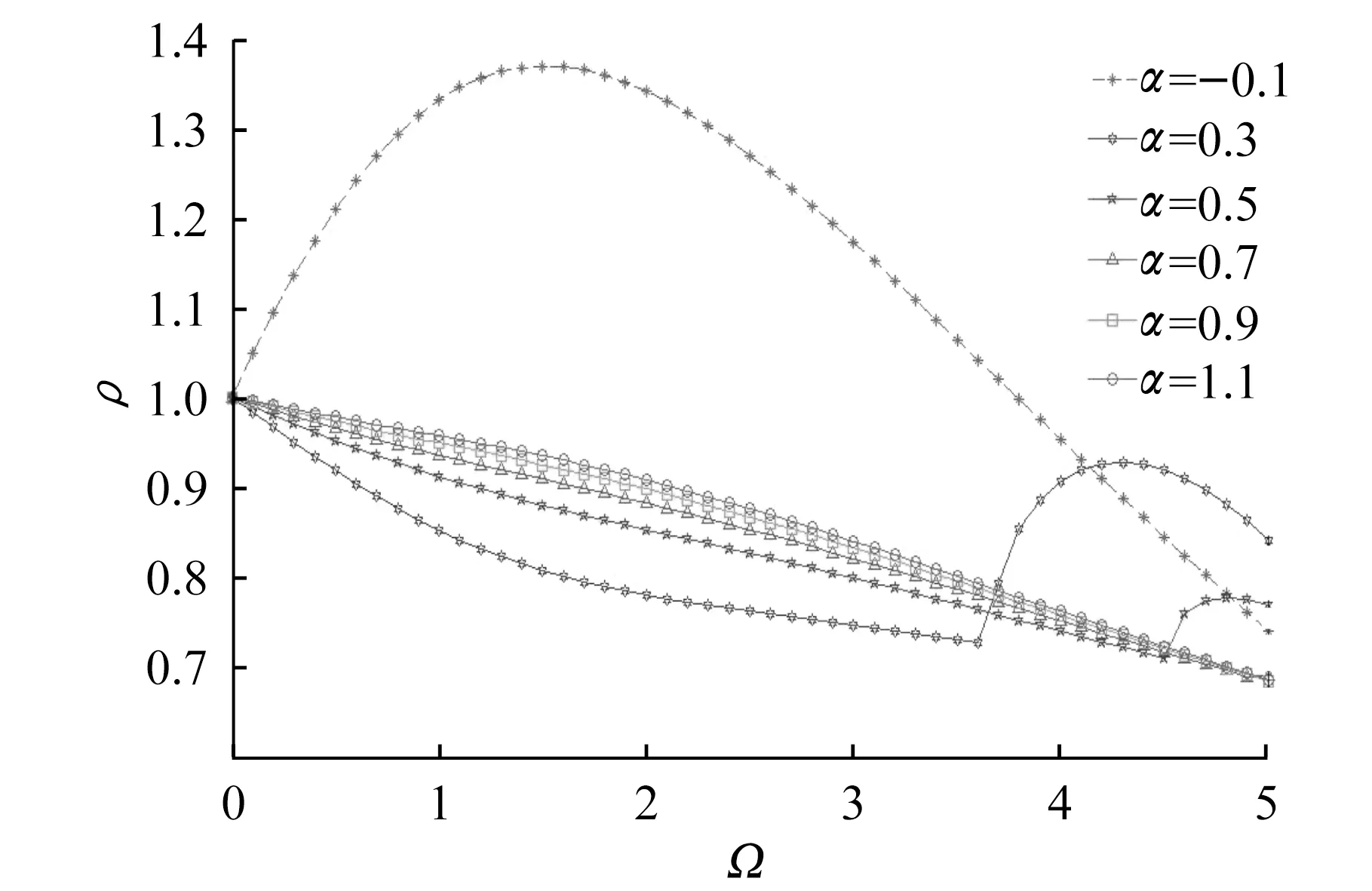
圖2 LSRT2法求解非線性阻尼單自由度結構的ρ-Ω關系曲線Fig.2 ρ-Ω curves of LSRT2 for solving nonlinear damping single-DOF structures

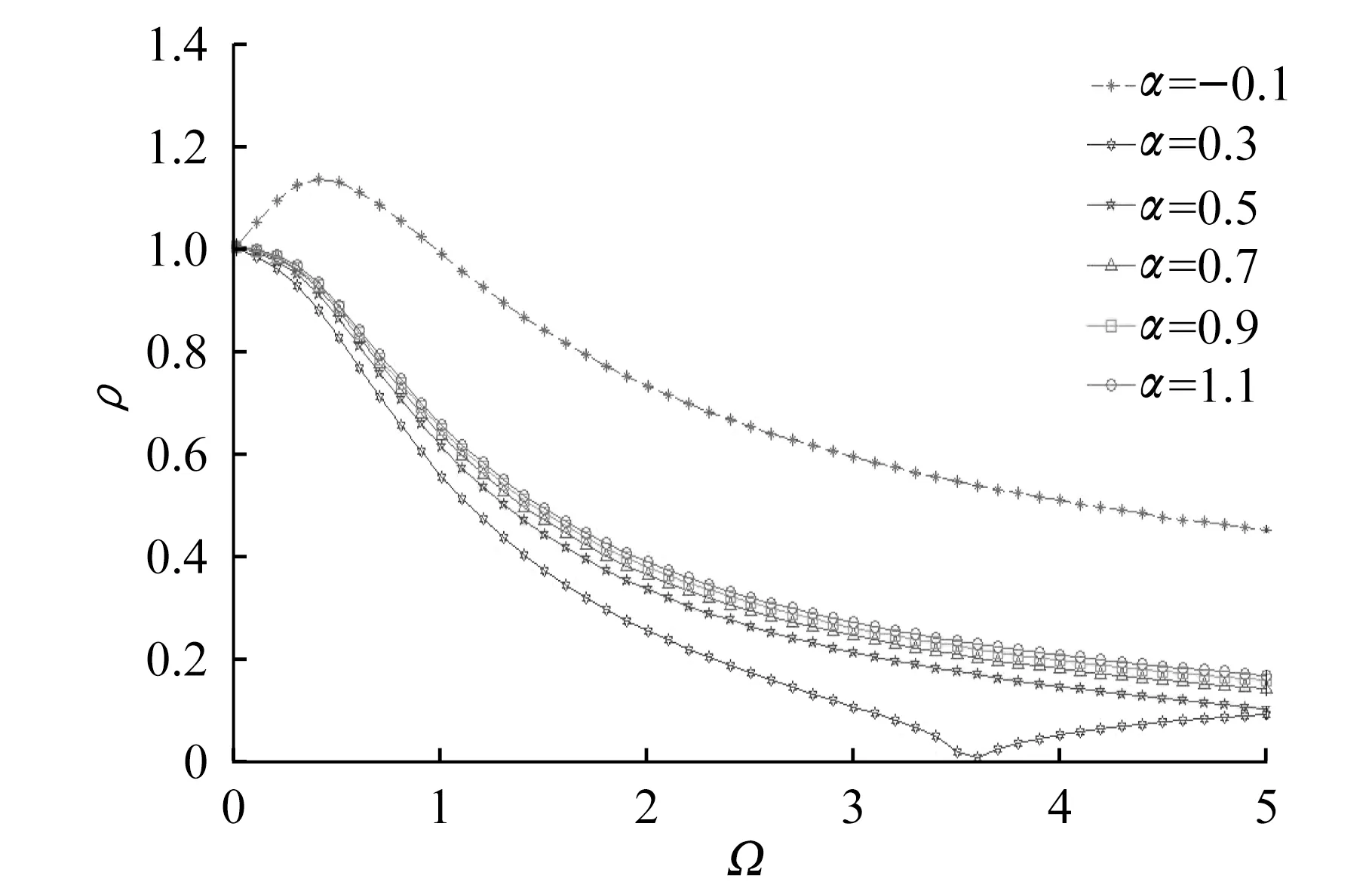
圖3 LSRT2法求解非線性阻尼單自由度結構的ρ-Ω關系曲線LFig.3 ρ-Ω curves of LSRT2 for solving nonlinear damping single-DOF structures

從圖2和圖3可見,當阻尼指數α>0時,LSRT2法放大矩陣對應的譜半徑ρ恒小于1;相反,當阻尼指數α<0時,在數值頻率Ω數值較小時LSRT2法放大矩陣對應的譜半徑ρ大于1,即其零穩定性[9]不滿足。譜分析法給出的結論可以解釋如下:當數值頻率Ω數值較小時(即采用的積分步長較小時),公式(18)右邊的速度相關項起到與左邊類似的阻尼作用。若0<α<1,則起到正阻尼作用,公式(18)本身是穩定的。當α=1時,右側速度相關項為0,公式(18)本身是穩定的線性運動方程。一般阻尼器,阻尼指數取值0<α≤1,但本文從數值分析角度,也對其他取值范圍進行研究。若α>1,右側速度相關項起到負阻尼作用,但公式(18)左邊有正阻尼項,總體效果是正阻尼作用。總之,當α>0,非線性阻尼器起到正阻尼的效果,采用LSRT2求解是穩定的。反之,當α<0,采用LSRT2求解有失穩現象。

6 數值算例

基于以上計算過程,對一安裝有非線性粘滯阻尼器的7層平面框架模型[20]進行數值模擬。結構為9度區7層鋼筋混凝土框架結構,抗震等級為一級,Ⅱ類場地,結構立面圖如圖4所示。其中,每層高度為3.3 m,柱截面尺寸為500 mm×500 mm,梁截面為600 mm×300 mm。

現取一榀框架進行計算,二維框架結構采用平面剛架模型。阻尼器在結構中的位置如圖4示,其阻尼力公式為F=1.8467v0.759 2。對于9度區,多遇地震加速度時程的最大值為0.14g。現采用El Centro波的x方向地震波對結構進行加載。整個計算過程(包括有限元建模和數值積分等)均在Matlab計算環境中完成。

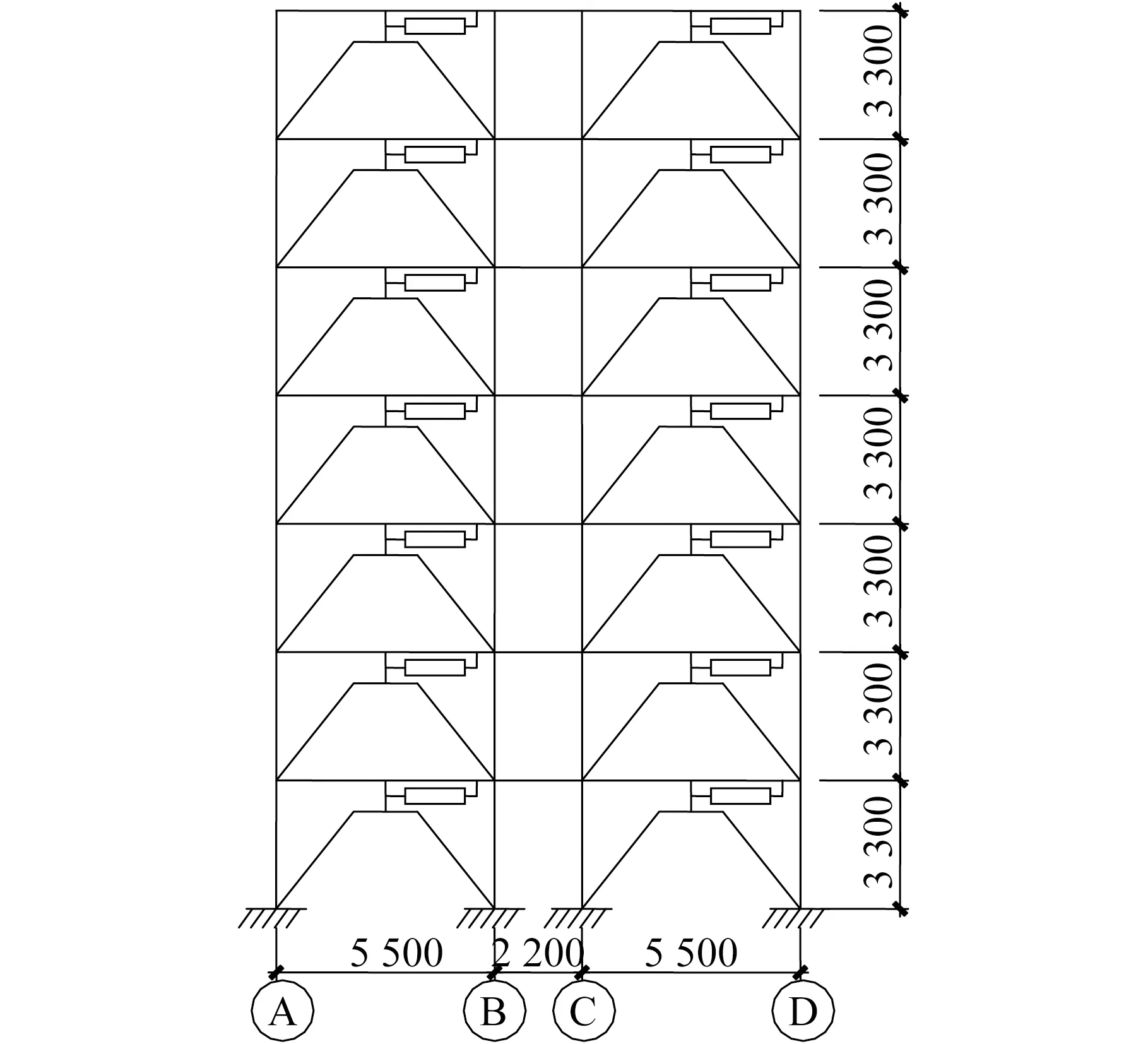
圖4 結構立面尺寸及阻尼器布置示意圖(單位:mm)Fig.4 The dimensions of the structure and the arrangement of the dampers (Unit:mm)

圖5為多遇地震下結構的頂點位移時程曲線(前15 s)。從圖5可以發現,采用改進前和改進后的LSRT2法計算所得的位移響應相近。但需要指出的是:采用LSRT2法,占用微機CPU的時間是28.314 2 s;而改進的LSRT2法占用CPU時間為8.546 8 s。因此,改進后計算效率大幅提高。

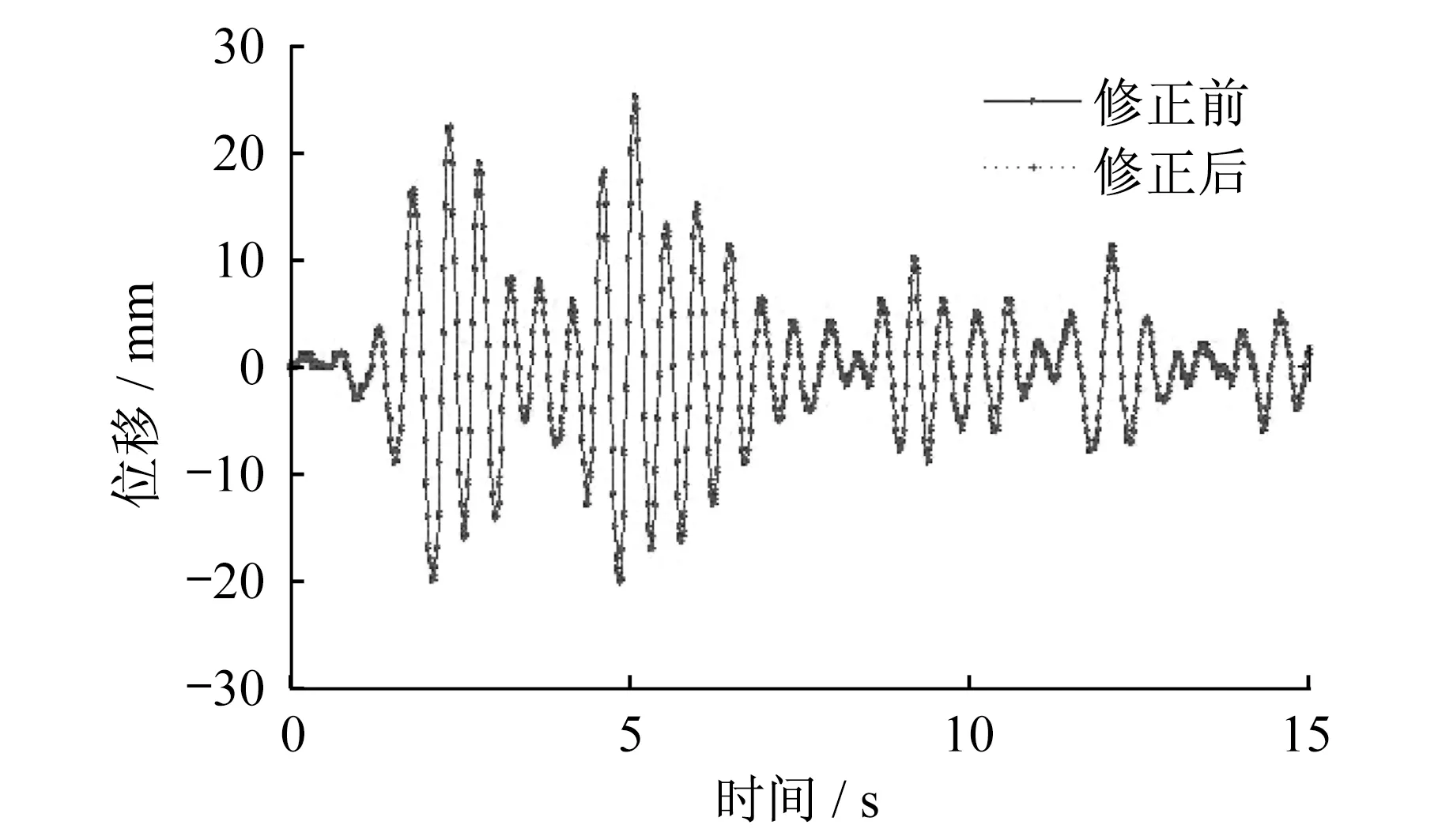
圖5 地震作用下結構頂層位移時程曲線Fig.5 Displacement time-history curves of structure topunder the action of earthquake

7 結 論

黏滯阻尼器等減震裝置一般局部設置在建筑結構的部分樓層,形成了典型的局部非線性問題。直接采用數值積分方法進行求解勢必導致計算量大和計算程序復雜等問題。于此,本文基于線性隱式的Rosenbrock積分方法,提出黏滯阻尼器減震結構地震響應分析方法。具體結論如下:

(1) 針對冪函數形式的非線性阻尼力,進行線性化處理,并引入阻尼器方位矩陣,形成了黏滯阻尼器減震結構運動方程。

(2) 在Rosenbrock方法中,引入Sherman-Morrison定理,簡化矩陣求逆的計算,形成求解局部非線性運動方程的方法。

(3) 對Rosenbrock方法求解非線性阻尼問題的穩定性進行了譜分析。結果表明,當阻尼指數大于0時,Rosenbrock方法是穩定的。

(4) 設計了一個裝有黏滯阻尼器的七層平面框架模型,通過編制Matlab程序進行了地震響應分析,結果證實本文所提方法的可靠性和計算效率。

本文相關處理方法對于位移型阻尼器減震結構的地震響應分析亦有參考價值。