考慮土體基質吸力剛性擋墻基坑抗傾覆穩定性分析

師晨翔 楊永平 馬際首 李鏡培,*

(1.同濟大學地下建筑與工程系,上海 200092; 2.上海南匯建工建設(集團)有限公司,上海 201399)

0 引 言

在大量的工程實踐中,地表降雨入滲是基坑工程、邊坡工程穩定性的重要影響因素,大量的工程實例和科學研究表明,入滲作用會引起土體中的吸力明顯降低,進而引起土體抗剪強度的降低,同時降雨入滲會提高土體的飽和度,增加作用在基坑圍護結構上的土壓力,對基坑的整體穩定性產生不利影響。因此,研究地表降雨入滲以及地下水位變化對土體性質和基坑穩定性的影響,具有非常重要的理論和工程意義。

截至目前,對非飽和土,基坑整體穩定性,以及土體基質吸力的問題,國內外學者已經開展了一系列有意義的研究。非飽和土真三軸試驗[1-2]的結果表明,土體強度與中間主應力大小關系密切。在基坑設計及穩定性驗算中,擋墻的抗傾覆穩定性是重要的內容,基坑周邊土體多為非飽和狀態,但是目前抗傾覆穩定性驗算還是使用基于Mohr-Coulomb(M-C)強度準則的飽和土理論[3],對土體非飽和的特性和中間主應力考慮不足。Lu 等[4-6]采用土-水特征參數α(進氣值)和n(孔隙大小參數)基于有效飽和度Se建立了非飽和土體吸應力σs計算公式。李兆平和張彌[7]應用非飽和土水分運動理論,結合Fredlund非飽和土強度理論研究了降雨入滲對基坑安全性的影響。關于非飽和土基坑擋墻抗傾覆穩定性的研究,吳劍敏等[8]研究了基質吸力對基坑支護結構內力的影響;尚軍[9]提出了基質吸力作用下,水泥攪拌樁抗滑移和抗傾覆穩定性的驗算方法;S.A.Stanier 和A.Tarantino[10]由極限分析上限定理確定了砂性非飽和土擋墻的張拉區深度。張常光等[11-13]利用拓展類比方法建立的非飽和土平面應變抗剪強度統一解能合理考慮中間主應力的影響,具有重要的工程應用價值。

可以看出,當前對非飽和土基坑抗傾覆穩定性分析等問題的研究取得了非常重要的進展,但是對降雨入滲,地下水位變化等問題考慮還不夠充分。在具體降雨強度、地下水位等的情況下,對基坑抗傾覆穩定性問題分析不夠精確,對工程實踐的指導意義不夠,難以對基坑抗傾覆進行動態監測及分析,缺乏在降雨條件下基坑穩定性檢測的理論指導。

在本文中,首先采用Gardner模型[14]定義的非飽和土水力傳導系數,結合達西定律,推導得出了地下水位面以上非飽和土體基質吸力的空間分布規律。進而基于非飽和土的平面應變抗剪強度統一解,考慮非飽和土強度的中間主應力效應,提出了考慮降雨入滲條件下,基坑擋墻抗傾覆穩定系數的計算方法,并進行參數影響特性分析,為非飽和土基坑支護結構的合理設計和施工提供一定的理論基礎。

1 降雨入滲條件基質吸力的分布規律

在Gardner模型[14]中,非飽和土體的水力傳導系數k表示為

k=kse-α(ua-uw)

(1)

式中:ks為飽和土體的水力傳導系數;(ua-uw)為基質吸力。

結合達西定律和Gardner模型,假設降雨條件下入滲強度為qs,且入滲強度恒定,可以得到地下水位線以上(Dw-y)處入滲條件下非飽和土體基質吸力的空間分布規律:

(2)

式中:α為SWCC曲線的擬合參數;α取值約為進氣壓的倒數;γw為水重度;Dw為地下水位線深度;y為地表以下深度;(Dw-y)表示地表深度y處與地下水位線的距離。

2 基坑擋墻抗傾覆穩定系數

張常光等[11-13]利用拓展類比方法建立的非飽和土平面應變抗剪強度統一解為

(3)

(4)

(5)

(6)

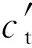
通過在式(4)-式(6)中引入統一強度理論參數,將中間主應力強度引入到土體抗剪強度的計算中。參數b取值大小的變化,反映土體抗剪強度準則的變化,b=0時不考慮中間主應力的影響,當b=1時,上述強度理論為基于雙剪應力強度理論的非飽和土體抗剪強度。

將式(2)代入式(3),可以得到降雨入滲條件下非飽和土平面應變抗剪強度計算公式:

(7)

非飽和土統一總黏聚力可以表示為

ctt=

(8)

本文的計算模型如圖1所示,地表降雨入滲強度均勻分布為qs,并且假設基坑擋墻為剛性擋墻,不考慮擋墻的自重、支撐、土體與基坑擋墻的摩擦,以及基坑周邊超載作用的影響。圖中,H表示基坑開挖深度;D表示擋墻抗傾覆嵌固深度;yot為墻后土體張拉區深度;Dw為地下水位深度,且位于擋墻墻趾以下;(σh-ua)a為作用在擋墻上的主動土壓力;(σh-ua)p為作用在擋墻上的被動土壓力。

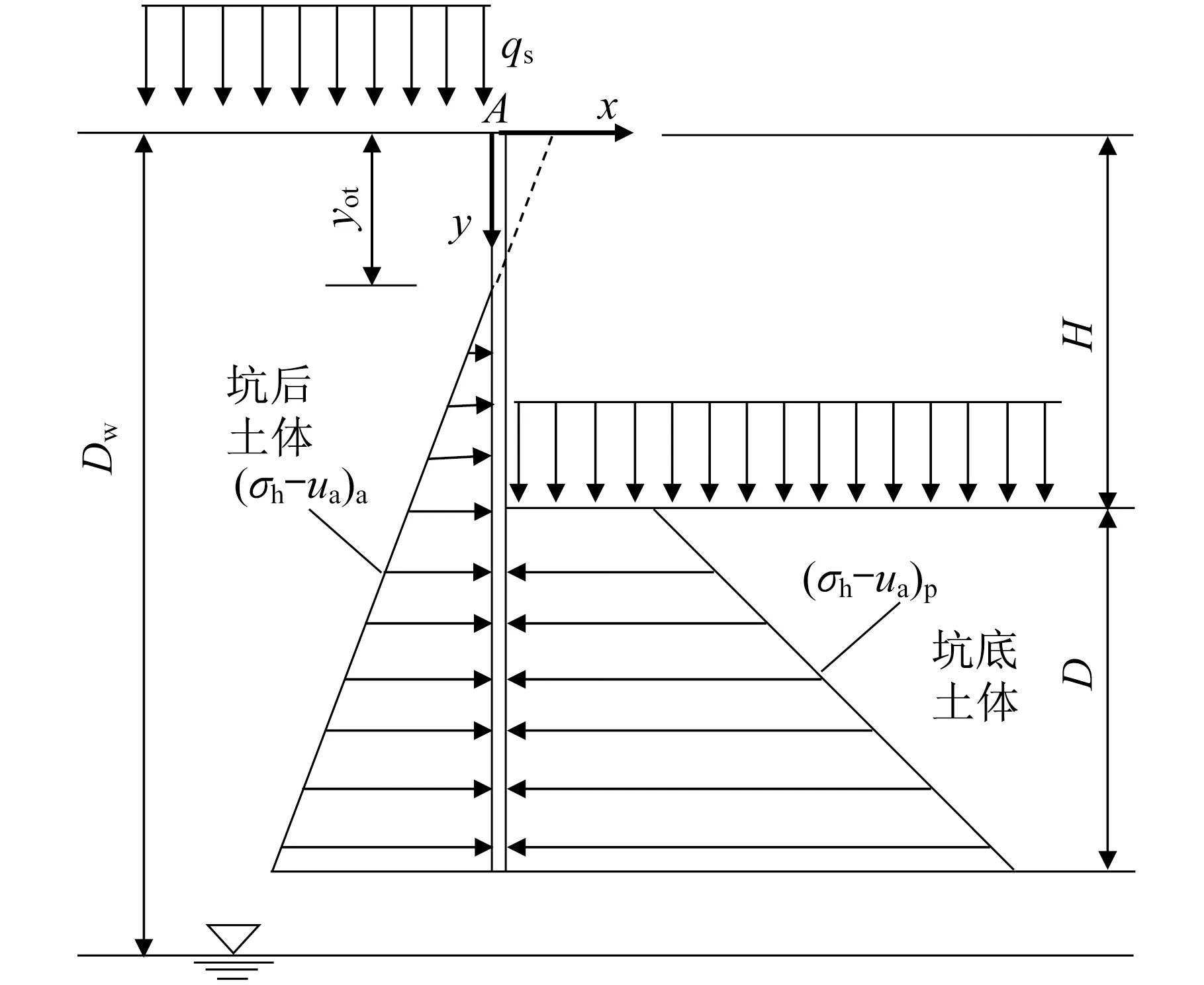
圖1 基坑降雨入滲條件下抗傾覆穩定性計算模型Fig.1 Calculation model of anti-overturning stability under infiltration

假設基坑周邊的土體為均勻連續的非飽和土層,基于朗肯理論,可以計算作用在剛性擋墻兩側的主動土壓力和被動土壓力。朗肯主動土壓力和被動土壓力的計算方法分別為:

主動土壓力強度(σh-ua)a為

(9)

式中:ka為主動土壓力系數;(σv-ua)a為主動土壓力區豎向應力大小,在此處(σv-ua)a=γy,其中,γ為非飽和土土體重度。

被動土壓力強度(σh-ua)p為

(10)

式中:kp為被動土壓力系數;(σv-ua)p為被動土壓力作用區域豎向應力大小,此處(σv-ua)p=γ(y-H)。

將式(8)代入式(9),得到考慮降雨入滲條件下非飽和土主動土壓力的計算公式:

(11)

在這里可以令式(11)中的主動土壓力強度(σh-ua)a=0,由此得到一個關于y的一元方程,可以借助計算機輔助計算,所求得的解為基坑擋墻后張拉區深度yot。

將式(8)代入式(10),得到考慮降雨入滲條件下非飽和被動土壓力的計算公式:

(12)

驗算基坑擋墻的抗傾覆穩定性時,通常假定擋墻繞其墻趾轉動,相應的計算公式為

(13)

式中:MSk為基坑外側產生的側壓力對墻趾產生的傾覆力矩;MRk為基坑內側墻被動土壓力產生的抗傾覆力矩。

對主動土壓力沿剛性擋墻深度進行積分可以得到墻體外側傾覆力矩MSk:

(14)

對被動土壓力沿剛性擋墻嵌入深度進行積分可以得到墻體外側傾覆力矩MRk:

(15)

將式(14)和式(15)分別代入式(13),可以得到基坑抗傾覆穩定系數Kq的計算方法:

(16)

在Kq的計算工程中,因為在(σh-ua)aw和(σh-ua)pw的公式推導中,都引入了基質吸力的空間分布,故在本抗傾覆穩定系數的計算中,充分考慮了地表降雨入滲,地下水位的變化對基坑抗傾覆穩定性的影響。

3 算例計算與參數影響特性分析

3.1 基坑抗傾覆參數影響分析

本算例假設在黏土地區的基坑中,開挖深度H為8 m,基坑擋墻嵌固深度D為10 m,起始地下水位深度Dw為18 m,有效黏聚力c′為3 kPa,有效內摩擦角φ′=20°,統一強度理論參數b=1,均質非飽和土體重度γ=19 kN/m3,α為SWCC曲線的擬合參數,α=0.005 kPa-1,地表入滲速率qs=0 m/s,飽和土體的水力傳導系數ks=5×10-8m/s,水體重度γw=10 kN/m3,吸力角φb=12°。

圖2給出了統一強度理論參數b分別為0～1時的基坑,分階段降水,基坑抗傾覆穩定系數Kq隨降水深度增加的變化規律。由圖8可以看出,b的不同取值,反映了中間主應力的考慮程度,對于b不同取值條件下,地下水位的下降會不同程度地提高抗傾覆穩定性。同時,伴隨著b取值增大,基坑抗傾覆穩定性明顯增加,這也充分說明,中間主應力在基坑抗傾覆穩定性的巨大影響。

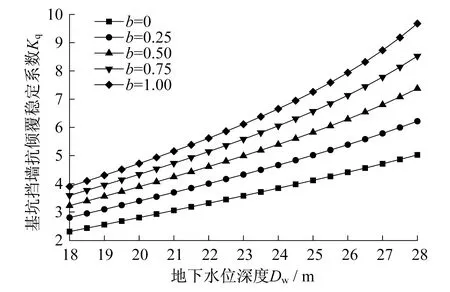
圖2 基坑抗傾覆穩定性隨地下水位的變化Fig.2 Variation of anti-overturning stability of the foundation pit under different de watering depths

圖3為基坑抗傾覆穩定系數Kq伴隨著統一強度理論參數b之間的關系,同時反映不同有效內摩擦角對基坑抗傾覆穩定性的影響。由圖可知,土體內摩擦角的變化對基坑抗傾覆穩定性有明顯影響,基坑抗傾覆穩定性隨內摩擦角的增大而增大。

圖3 中間主應力對基坑抗傾覆穩定性的影響Fig.3 Effect of intermediate principal stress on anti-overturning stability of the foundation pit

圖4展現了基坑擋墻在不同嵌固深度下,基坑抗傾覆穩定性與統一強度理論參數b之間的關系。從圖中可知,基坑嵌固深度的增加有利于增加基坑抗傾覆穩定性,中間主應力對基坑抗傾覆穩定性有益。

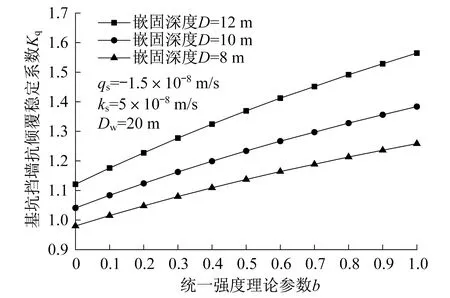
圖4 嵌固深度對基坑抗傾覆穩定性的影響Fig.4 Effect of embedment depth on anti-overturning stability of the foundation pit

3.2 降雨入滲條件影響分析

圖5反映了不同入滲條件下,本文計算方法基質吸水位面以上的空間分布規律。從圖中可以看出,在沒有降雨入滲條件下,基質吸力隨距離地下水位線高度的增加展現出線性單調增大的趨勢,對應圖1中基坑抗傾覆計算模型,地下水位線以上土體,豎向距離越遠,土體中基質吸力越大。降雨入滲條件下,基質吸力的大小明顯降低,并且入滲強度越大,基質吸力強度幅度越大,同時基質吸力距離地下水位線高度的增加,其增幅有逐漸放緩的趨勢。

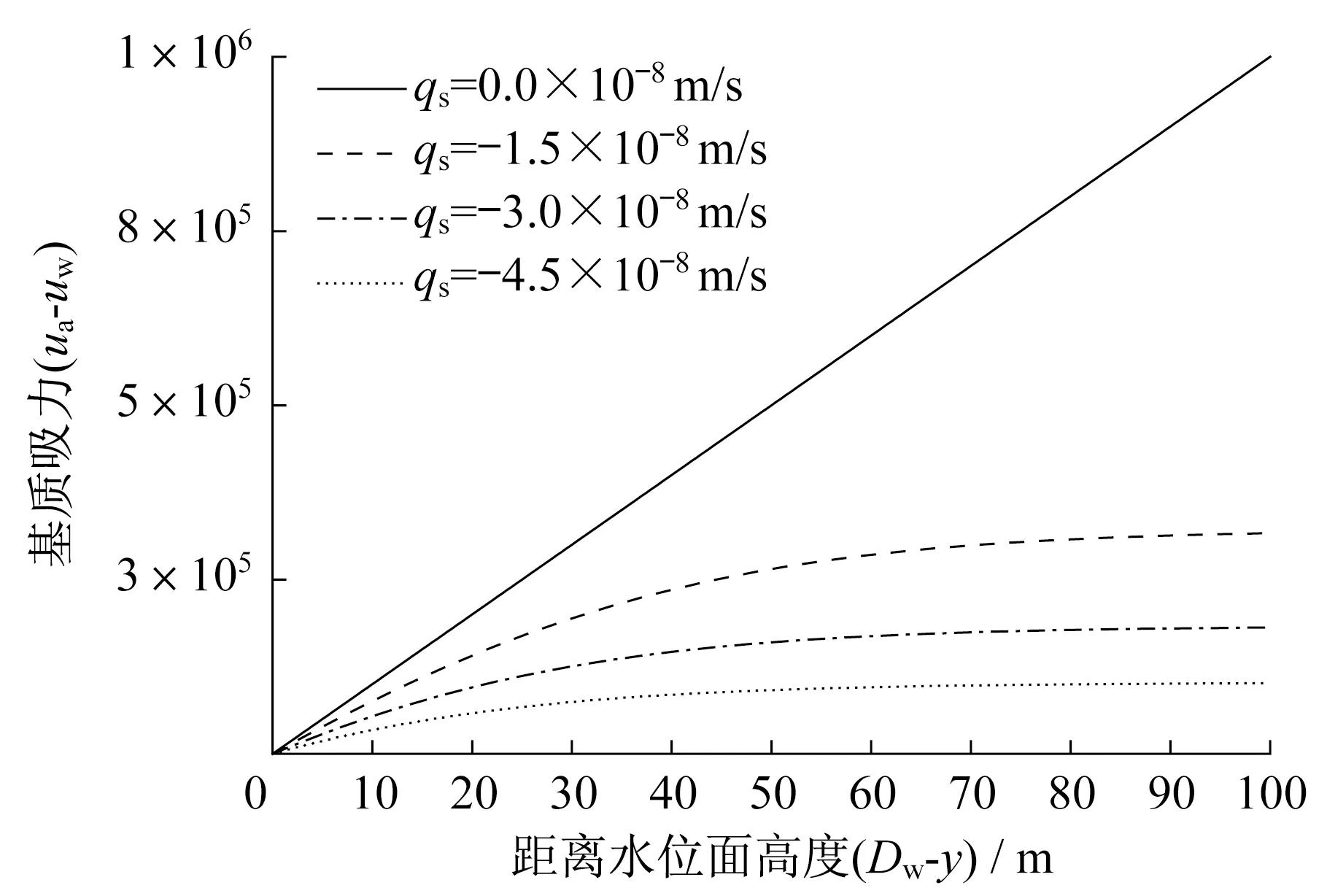
圖5 地下水位線以上土體基質吸力空間分布規律Fig.5 Distribution of soil matric suction above the ground water table in soil

圖6中給出了,不同降雨入滲條件下,基坑地下水位不同位置情況下,基坑擋墻的抗傾覆穩定系數Kq的變化規律。從圖中可以看出,降雨入滲對基坑抗傾覆穩定性有明顯影響,伴隨著降雨入滲強度的增強,基坑抗傾覆穩定性降低。同時,降雨入滲強度增大時,基坑伴隨地下水位降低抗傾覆穩定系數增長的幅度較小。

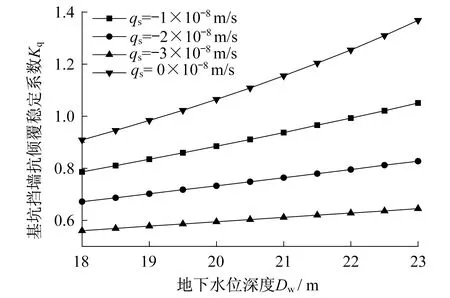
圖6 降雨入滲對基坑抗傾覆穩定性的影響Fig.6 Effect of the infiltration on anti-overturning stability of the foundation pit

3.3 不同基質吸力分布形式對比

為了進一步研究本文降雨入滲條件對基坑抗傾覆穩定性的影響,在此與工程中常用基質吸力計算方法相比較。基質吸力是非飽和土與飽和土的一個重要區別,與降雨,蒸發等因素關系密切,目前在工程應用中,主要采用近似假定基質吸力均勻分布,或者沿深度線性減少到地下水位Dw處這兩種方式,如圖7所示。

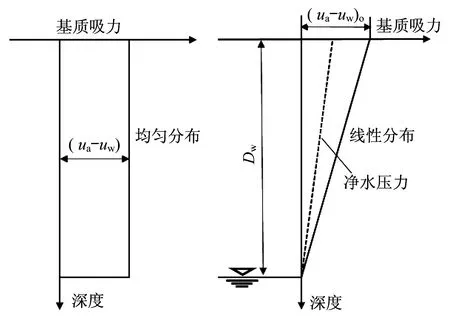
圖7 基質吸力分布Fig.7 Distribution of soil matric suction

圖8分別給出了本文基質吸力算法與基質吸力均勻分布和基質吸力沿深度線性分布條件下,基坑擋墻抗傾覆穩定系數Kq與統一強度理論參數b的關系圖。從圖中可以看出,隨著地表基質吸力的增加,基坑抗傾覆安全系數Kq不斷增加。從中可以看出,基坑擋墻抗傾覆計算中,忽略基質吸力對非飽和土強度的影響,計算將偏保守。同時,有圖8(a)和圖8(b)對比可以看出,相同地表強度下,按照基質吸力沿深度減小到地下水位為0的算法,基坑抗傾覆穩定性計算更加保守。相比與均勻分布和線性遞減的基質吸力分布,本文方法可以根據入滲強度,土體性質,計算基質吸力的具體分布,計算更加精確。

圖8 基質吸力分布方式對基坑抗傾覆穩定性的影響Fig.8 Effect of the distribution of soil matric suction on anti-overturning stability of the foundation pit

4 結 論

本文基于非飽和土的平面應變抗剪強度統一解,推導了降雨入滲條件下基坑抗傾覆穩定性計算公式。分析了降雨入滲強度,嵌固深度,土體內摩擦角,統一強度理論參數等因素對基坑抗傾覆穩定性的影響,通過算例分析和方法對比,可以得出以下結論:

(1) 中間主應力σ2對基坑抗傾覆穩定性驗算有較大影響。通過參數b的引入,考慮中間主應力σ2效應,在基坑抗傾覆計算中可以更好地考慮非飽和土的強度潛能,更客觀地反映基坑抗傾覆穩定性。

(2) 基坑抗傾覆穩定性與地下水位深度密切相關。基坑降水對土體強度有直接影響,伴隨著基坑降水深度的增加,土體基質吸力的作用增強,提高了土體的強度,同時減少土體重度,提高基坑抗傾覆穩定性。

(3) 降雨入滲對基坑抗傾覆存在重大影響。降雨入滲強度的增加,會明顯改變基質吸力的分布,并且降低基質吸力的大小,進而對土體強度產生不利影響,降低基坑抗傾覆穩定性。

(4) 土體內摩擦角對基坑抗傾覆穩定性存在較大影響。土體內摩擦角增大,土體基質吸力產生的粘聚力提高,進而增大了抗剪強度,對基坑抗傾覆穩定性有益。

(5) 基坑擋墻嵌固深度與基坑抗傾覆穩定性關系密切,增加擋墻嵌固深度有利于基坑抗傾覆穩定性的提高。