小議正五邊形

單勤海

在某次解題比賽中有一道關于折紙的問題。該題采用了常見的一種紙條折疊方法討論了一個五邊形的問題，引起了不少數學教師的興趣。現將原題呈現如下：

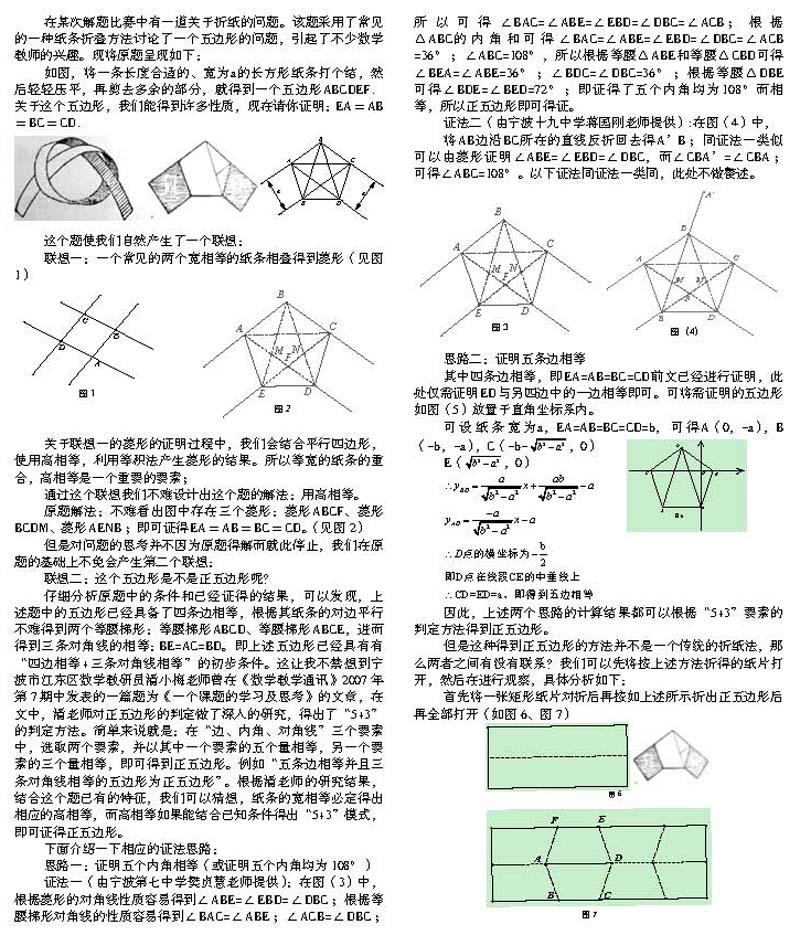
如圖，將一條長度合適的、寬為a的長方形紙條打個結，然后輕輕壓平，再剪去多余的部分，就得到一個五邊形ABCDEF.關于這個五邊形，我們能得到許多性質，現在請你證明： EA=AB=BC=CD.

這個題使我們自然產生了一個聯想：

聯想一：一個常見的兩個寬相等的紙條相疊得到菱形（見圖1）

關于聯想一的菱形的證明過程中，我們會結合平行四邊形，使用高相等，利用等積法產生菱形的結果。所以等寬的紙條的重合，高相等是一個重要的要素；

通過這個聯想我們不難設計出這個題的解法：用高相等。

原題解法：不難看出圖中存在三個菱形：菱形ABCF、菱形BCDM、菱形AENB；即可證得EA=AB=BC=CD。（見圖2）

但是對問題的思考并不因為原題得解而就此停止，我們在原題的基礎上不免會產生第二個聯想：

聯想二：這個五邊形是不是正五邊形呢？

仔細分析原題中的條件和已經證得的結果，可以發現，上述題中的五邊形已經具備了四條邊相等，根據其紙條的對邊平行不難得到兩個等腰梯形：等腰梯形ABCD、等腰梯形ABCE，進而得到三條對角線的相等：BE=AC=BD。即上述五邊形已經具有有“四邊相等+三條對角線相等”的初步條件。這讓我不禁想到寧波市江東區數學教研員潘小梅老師曾在《數學教學通訊》2007年第7期中發表的一篇題為《一個課題的學習及思考》的文章，在文中，潘老師對正五邊形的判定做了深入的研究，得出了“5+3”的判定方法。簡單來說就是：在“邊、內角、對角線”三個要素中，選取兩個要素，并以其中一個要素的五個量相等，另一個要素的三個量相等，即可得到正五邊形。例如“五條邊相等并且三條對角線相等的五邊形為正五邊形”。根據潘老師的研究結果，結合這個題已有的特征，我們可以猜想，紙條的寬相等必定得出相應的高相等，而高相等如果能結合已知條件得出“5+3”模式，即可證得正五邊形。

下面介紹一下相應的證法思路：

思路一：證明五個內角相等（或證明五個內角均為108°）

證法一（由寧波第七中學樊貞慧老師提供）：在圖（3）中，根據菱形的對角線性質容易得到∠ABE=∠EBD=∠DBC；根據等腰梯形對角線的性質容易得到∠BAC=∠ABE；∠ACB=∠DBC；所以可得∠BAC=∠ABE=∠EBD=∠DBC=∠ACB；根據△ABC的內角和可得∠BAC=∠ABE=∠EBD=∠DBC=∠ACB =36°；∠ABC=108°，所以根據等腰△ABE和等腰△CBD可得∠BEA=∠ABE=36°；∠BDC=∠DBC=36°；根據等腰△DBE可得∠BDE=∠BED=72°；即證得了五個內角均為108°而相等，所以正五邊形即可得證。

證法二（由寧波十九中學蔣國剛老師提供）：在圖（4）中，

將AB邊沿BC所在的直線反折回去得AB；同證法一類似可以由菱形證明∠ABE=∠EBD=∠DBC，而∠CBA=∠CBA；可得∠ABC=108°。以下證法同證法一類同，此處不做贅述。

思路二：證明五條邊相等

其中四條邊相等，即EA=AB=BC=CD前文已經進行證明，此處僅需證明ED與另四邊中的一邊相等即可。可將需證明的五邊形如圖（5）放置于直角坐標系內。

可設紙條寬為a，EA=AB=BC=CD=b，可得A（0，-a），B（-b，-a），C（-b-，0）

E（，0）

因此，上述兩個思路的計算結果都可以根據“5+3”要素的判定方法得到正五邊形。

但是這種得到正五邊形的方法并不是一個傳統的折紙法，那么兩者之間有沒有聯系？我們可以先將按上述方法折得的紙片打開，然后在進行觀察，具體分析如下：

首先將一張矩形紙片對折后再按如上述所示折出正五邊形后再全部打開（如圖6、圖7）

根據折疊的方法，容易得到打開后的折痕六邊形ABCDEF為六條邊相等的非正六邊形，且AD恰好是圖6中的正五邊形的一條對角線，因此根據原正五邊形易得

然后將紙條沿AC折疊（如圖8），易得B點落在AD上的G點處，沿CG折疊，得折痕CG，同理得折痕BH（如圖9），折痕CG與折痕BH相交于點P，沿直線AP和DP折疊，易證得五邊形PABCD即為正五邊形，且與圖6中的正五邊形相似。

既然折疊可以得到正五邊形，那么尺規作圖能否得到正五邊形呢？對于這一點很多老師都不陌生，但是基本上都是借助圓內得等分來作圖。但是正五邊形由于其特殊性，我們也可以采用黃金分割線的特點進行作圖。具體如下（如圖10）：

①先作出AB=2AC，∠A=90°的Rt△ABC，取得AB邊上的黃金分割點E；

②以A為圓心，BE為半徑作圓；以B為圓心，AB為半徑作圓；兩圓交于點C；

③作AB的中垂線，與以B為圓心，以BE為半徑的圓相交于點G；

④作BC的中垂線，與以B為圓心，以BE為半徑的圓相交于點H；

⑤順次連結B、G、A、C、H，得正五邊形BGACH；

現在我們可以看到，通過折疊和尺規作圖都能得到正五邊形，那么是否折疊問題和尺規作圖問題之間能夠互相轉化呢？其實，并不盡然。尺規作圖與折疊圖形之間雖然有某些聯系存在，但是還是具有一定的區別。

首先，對于尺規作圖來說，主要能夠作出三個基本作圖要素：

①直線型。主要是線段、射線和直線；

②曲線型。主要是圓和弧；

③點型。主要是直線與直線的交點；尋找圓與直線的交點；尋找圓與圓的交點。

而折疊的基本作圖要素主要有四個：

①折疊，使兩個已知點重合；

②折疊，使一個已知點落在某條已知直線上；

③折疊，使兩條已知直線重合；

④折疊，使一條已知直線與自身重合；

將兩者的要素進行對照，就可以發現，在曲線方面尺規作圖要強于折疊，但是在直線型問題和點型問題的解決上折疊比尺規作圖要強大的多。正因為如此，在正七邊形的問題上，只能通過折疊得到，而無法用尺規作圖得到。（但是能夠通過尺規作圖能到近似的正七邊形，詳見《鉗工手冊》）

綜上所述，培養學生的折疊技能和方法是提高學生數學思維和數學操作動手能力的有效途徑，學生通過折疊的學習，既能夠提高對數學的學習興趣，又能夠掌握和提高數學的空間想象能力和分析解決問題的應用能力。