半正二階三點邊值問題正解的分歧結(jié)構(gòu)

張 露, 劉喜蘭

(青海民族大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 青海 西寧 810007)

1 引言及預(yù)備知識

二階微分方程在應(yīng)用數(shù)學(xué)與物理領(lǐng)域中有著極為廣泛的應(yīng)用,例如工程學(xué)上均勻桿軸向受力問題、由N部分不同密度構(gòu)成的金屬支索絲一致截面的振動問題等[1].基于其豐富的實際應(yīng)用背景,二階非線性常微分方程邊值問題正解的存在性問題在整個常微分方程研究領(lǐng)域顯得尤為重要.對于經(jīng)典的邊值問題,已取得深入而系統(tǒng)的結(jié)果,而對非局部邊值問題的研究也日臻成熟,參見文獻(xiàn)[2-15].

Ma[2]率先研究三點邊值問題

正解的存在性,提出了研究這類問題的關(guān)鍵條件

0<αη<1,

并在非線性項滿足超線性或次線性的前提下,運用錐上的不動點定理建立了正解的存在性結(jié)果.文獻(xiàn)[3-6]等將上述結(jié)果推廣和發(fā)展到更廣泛的邊界條件及更一般的線性微分算子的情形.

值得注意的是,大多數(shù)研究結(jié)果都是建立在非線性項非負(fù)的前提下,而對于非線性項允許取負(fù)值的情形,研究相對較少,見文獻(xiàn)[6-7].

Yao[6]借助于錐上的不動點定理考慮了半正問題

(1)

正解的存在性.Xu[7]運用不動點指數(shù)理論對半正問題(1)中λ=1的情形,給出了多個正解的存在性結(jié)果.

(H1)λ>0為參數(shù),f∈C([0,1]×[0,+∞),R),且對任意的t∈(0,1),有f(t,0)<0;

(H2) 存在m>0,使得

對t∈(0,1)一致成立.

令X=C[0,1],則X按范數(shù)

構(gòu)成Banach空間.

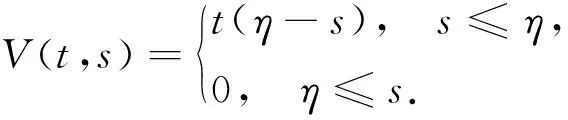
通過簡單計算可得G:[0,1]×[0,1]→[0,∞)連續(xù)非負(fù)且G(t,s)>0,?t,s∈(0,1)×(0,1).

定義Hilbert空間L2(0,1)中的內(nèi)積為

令

B={u∈C2[0,1]:u(0)=0,u(1)=αu(η)},

顯然B與B*都是L2(0,1)的子空間.對u∈B,記算子Lu=-u″,對v∈B*,記算子L*v=-v″,則有引理1.2.

引理1.2對任意的u∈B,v∈B*,有(Lu,v)=(u,L*v).

證明對任意的u∈B,v∈B*,

所以,對任意的u∈B,v∈B*,有(Lu,v)=(u,L*v).

根據(jù)前面的討論可知,問題

(2)

為問題(1)的共軛問題.

稱u是問題(2)的解，是指u∈B*且滿足L*u=λf(t,u(t)),即

其中,u1(t)是問題

(3)

在C2[0,η]中的解,u2(t)是問題

(4)

在C2[η,1]中的解,且滿足

引理1.3設(shè)G*(t,s)為問題(2)的Green函數(shù),則G*(t,s)=G(s,t).

若0≤t≤η,則

f(s,u(s))ds,

顯然u(0)=0.

u″(t)=-λf(t,u(t)),

所以u(t)在[0,η]上二階連續(xù)可導(dǎo),并滿足(3)式.

若η≤t≤1,則

顯然u(1)=0.

u″(t)=-λf(t,u(t)),

定義算子K:X→X為

記K的伴隨算子為

(5)

引理1.4(5)式所定義的K*為線性全連續(xù)算子.令r(K*)表示K*的譜半徑,則r(K*)>0,且存在ψ1∈X滿足?t∈(0,1),ψ1(t)>0,使得K*ψ1=r(K*)ψ1.

(6)

存在主特征值λ1>0,其所對應(yīng)的特征函數(shù)φ1>0,t∈(0,1),且‖φ1‖=1.

證明因為φ1滿足(6)式,則有

對上式兩邊同時乘ψ1,在0到1上積分得

由引理1.1可知,問題(1)等價于算子方程

u-λKf(t,u)=0,u∈X.

(7)

稱(λ∞,∞)為問題(7)從無窮遠(yuǎn)處產(chǎn)生的分歧點,是指存在(μn,un)∈R×X滿足(7)式,使得μn→λ∞,‖un‖→∞.

2 主要結(jié)果及證明

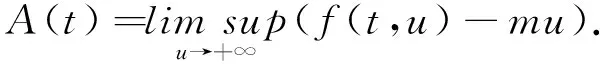
定理2.1假定條件(H1)和(H2)成立,若存在ε>0使得下列條件之一成立:

(i) 對任意的t∈(0,1),a(t)>0,且λ∈[λ∞-ε,λ∞);

(ii) 對任意的t∈(0,1),A(t)<0,且λ∈(λ∞,λ∞+ε],

則問題(1)至少存在一個正解.

首先,將f(t,·)延拓，使其定義在整個實數(shù)集R,即

定義

Φ(λ,u):=u-λKF(u), ?u∈X.

若對任意的u>0,使得Φ(λ,u)=0成立,則u為方程(1)的解.

為了證明定理1,首先需證明下面3個引理.

引理2.2對任意的緊區(qū)間Λ?R+{λ∞},存在r>0,使得對任意的λ∈Λ,‖u‖≥r,有Φ(λ,u)≠0.進(jìn)一步,

(i) 若a(t)>0,可取Λ=[λ∞,λ],?λ>λ∞;

(ii) 若A(t)<0,可取Λ=[0,λ∞].

證明反設(shè)存在μn→μ≥0,μ≠λ∞,且‖un‖→∞,滿足

un=μnKF(un).

ωn=μn‖un‖-1KF(un).

則由引理1.1及μm|ω|≥0知ω≥0.又因‖ω‖=1,所以μm=λ1,這與μ≠λ∞矛盾.故結(jié)論成立.

下面證明當(dāng)a(t)>0時,Λ=[λ∞,λ],?λ>λ∞.

-ω″(t)=μm|ω(t)|,t∈(0,1),

又因un滿足

(8)

對(8)式兩邊同時乘ψ1,在0到1上積分,由引理1.6得

從而

由Fatou引理得

mun(t)]ψ1(t)dt≤0,

這與a>0矛盾.對A(t)<0的情形類似可證,此處略去.

引理2.3對λ>λ∞,存在r>0使得對任意的τ≥0,‖u‖≥r,有Φ(λ,u)≠τφ1.

證明反設(shè)存在τn≥0,‖un‖→∞,滿足Φ(λ,u)=τnφ1,則有

τnφ1(t).

(9)

由條件(H2)知,當(dāng)n充分大時,

f(t,|un|)?m|un|,

則由引理1.1可知un≥0.所以f(t,|un|)=f(t,un).對(9)式兩邊同時乘ψ1,在0到1上積分得

所以

(10)

由條件(H2)知,當(dāng)n→∞時有

對上式兩端取極限得:λ1≥λm>λ∞m=λ1,矛盾.

Ψ(λ,z)=‖u‖-2Φ(λ,u)=

則由拓?fù)涠鹊耐瑐惒蛔冃缘?/p>

(11)

當(dāng)λ>λ∞時,由引理2.3知,?t∈[0,1],?u∈X,當(dāng)‖u‖≥r時有Φ(λ,u)≠t‖u‖2φ1,從而

ψ(λ,z)≠tφ1, ?t∈[0,1],

因此

(12)

令

Σ={(λ,u)∈R+×X:u≠0,Φ(λ,u)=0},

由(11)和(12)式得到下面的引理.

引理2.4(λ∞,∞)為(7)式從無窮遠(yuǎn)處產(chǎn)生的分歧點,即存在從無窮遠(yuǎn)處產(chǎn)生的無界連通分支Σ∞?Σ.進(jìn)一步,若a>0,則Σ∞向左分歧,若A<0,則Σ∞向右分歧.

定理2.1的證明根據(jù)引理2.2～2.4知,存在問題(1)的解(μn,un)滿足μn→λ∞,‖un‖→∞,則對充分大的n及t∈(0,1)有un>0成立.

[1] TIMOSHENKO S, GERE J. Theory of Elastic Stability[M]. New York:McGraw-Hill,1962:35-48.

[2] LIU B. Positive solutions of a nonlinear three-point boundary value problem[J]. Electronic J Diff Eqns,1999,132(1):11-28.

[3] WEBB J. Positive solutions of some three point boundary value problems via fixed point index theory[J]. Nonlinear Analysis,2001,47(7):4319-4332.

[4] INFANTE G. Eigenvalues of some non-local boundary-value problems[J]. Pro Edinburgh Mathematical Society,2003,46(1):75-86.

[5] LIU B. Positive solutions of a nonlinear three-point boundary value problem[J]. Comput Math Appl,2002,44(1):201-211.

[6] YAO Q. An existence theorem of positive solution for a superlinear semipositone second-order three-point BVP[J]. Mathematical Study,2002,35(1):33.

[7] XU X. Multiplicity results for positive solutions of some semi-positone three-point boundary value problems[J]. J Math Anal Appl,2004,291(2):673-689.

[8] AMBROSETTI A, ARCOYA D, BUFFONI B. Positive solutions for some semi-positone problems via bifurcation theory[J]. Diff Iniegral Eqns,1994,7(1):655-663.

[9] MA R, WANG H. Positive solutions for a nonlinear three-point boundary value problem[J]. J Math Anal Appl,2003,297(1):1216-1227.

[10] 鄭春華,劉文斌. 一類p-Laplacian方程非局部問題解的存在性[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2013,36(6):856-861.

[11] 張露,馬如云. 漸近線性二階半正離散邊值問題正解的分歧結(jié)構(gòu)[J]. 山東大學(xué)學(xué)報(理學(xué)版),2014,49(3):73-83.

[12] 李玉環(huán),余萍,李玲. 一類半線性拋物方程非局部問題的整體解[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2004,27(6):579-580.

[13] MA R. Positive solutions of three point nonlinear discrete second order boundary value problems[J]. J Diff Eqns Appl,2004,10(2):129-138.

[14] MERDIVENCI F. Two positive solutions of a boundary value problem for difference equations[J]. J Diff Eqns Appl,1995,1995(1):262-270.

[15] DAI G, MA R. Unilateral global bifurcation phenomena and nodal solutions forp-Laplacian[J]. J Diff Eqns,2012,2012(252):2448-2468.

[16] ZEIDLER E. Nonlinear Functional Analysis and Its Applications:I:Fixed-Point Theorems[M]. New York:Springer-Verlag,1985:15.