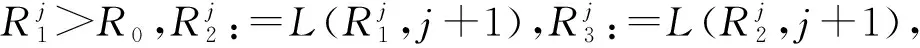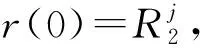一類雙質(zhì)子耦合格點(diǎn)系統(tǒng)的對(duì)稱周期解

王 超, 黃娟娟, 楊 瀟

(鹽城師范學(xué)院 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 江蘇 鹽城 224001)

1 引言及預(yù)備知識(shí)

本文考慮雙質(zhì)子耦合格點(diǎn)系統(tǒng)

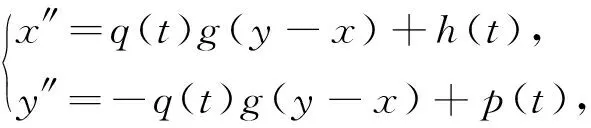
(1)

其中h、p是連續(xù)的2π-周期偶函數(shù)且滿足

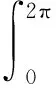
權(quán)函數(shù)q(t):R→R+為2π-周期連續(xù)函數(shù),g:R→R是局部Lipschitz連續(xù)函數(shù)且滿足

一維質(zhì)子鏈系統(tǒng)具有廣泛的應(yīng)用背景.例如,對(duì)于系統(tǒng)(1),當(dāng)q(t)≡A∈R,g:R+→R+在原點(diǎn)具有奇性時(shí),系統(tǒng)(1)可以刻劃在一條直線上的2個(gè)受迫充電質(zhì)子的運(yùn)動(dòng)[1].在文獻(xiàn)[1]中,Torres等討論了周期解存在的充分必要條件,他們通過使用變量代換的方法對(duì)系統(tǒng)進(jìn)行降維后得到文獻(xiàn)[1]中的結(jié)果,并在文獻(xiàn)[2-3]中把結(jié)果推廣到無限維的情形.另外,在文獻(xiàn)[2-3]中對(duì)Toda鏈的情形也進(jìn)行了討論.關(guān)于一維質(zhì)子鏈系統(tǒng)的研究有許多工作,涉及到解的動(dòng)力行為的許多特征,如周期解[4-5]、擬周期解的不變環(huán)面[6]、離散孤立子和呼吸子[7]、同宿行波解的存在性[8]以及指數(shù)吸引子[9]等,其中,文獻(xiàn)[4，6-7]涉及到時(shí)變的FPU鏈.

定義1.1函數(shù)(x(t),y(t))稱為方程(1)偶的2kπ-周期解(k∈Z+),如果對(duì)正整數(shù)k有

(x(0),y(0))=(x(2kπ),y(2kπ)),(x′(0),y′(0))=(x′(2kπ),y′(2kπ)),

且對(duì)任意t∈[0,2kπ]都有

(x(-t),y(-t))=(x(t),y(t)).

特別地,當(dāng)k=1時(shí),稱(x(t),y(t))為方程(1)偶的調(diào)和解;當(dāng)k>1時(shí),稱(x(t),y(t))為方程(1)偶的次調(diào)和解.

關(guān)于方程對(duì)稱周期解的討論也是動(dòng)力系統(tǒng)的一個(gè)有趣問題,它與方程的穩(wěn)定性問題有關(guān).一個(gè)經(jīng)典的工作是Nakajima在文獻(xiàn)[10]中證明了Duffing方程無窮多個(gè)對(duì)稱調(diào)和解的存在性以及對(duì)稱次調(diào)和解的稠密性分布結(jié)果.在文獻(xiàn)[1]中,作者考慮二階方程

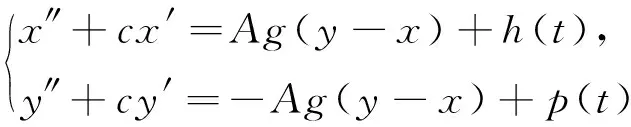
(2)

的周期解問題時(shí),主要的證明方法還是降維.通過討論降維后2個(gè)非耦合方程周期解的存在性來推斷原來系統(tǒng)周期解的存在性問題;但當(dāng)方程是偶對(duì)稱方程時(shí),證明方程是否存在偶的周期解并不是一件容易的事.事實(shí)上,對(duì)降維后的等價(jià)方程而言,即使能夠證明其中一個(gè)方程具有偶的周期解,也不能輕易看出另一個(gè)非耦合方程也具有偶的周期解.

針對(duì)上述主要困難,本文在引理1.1中解決了這一問題.我們證明:對(duì)于降維后的等價(jià)方程組,只要其中一個(gè)非耦合方程具有偶的周期解,則原系統(tǒng)一定存在與之對(duì)應(yīng)的偶的周期解.

令

為二階自治方程x″+g(x)=0的軌道

上的周期解的最小正周期,其中

且e為充分大的正實(shí)數(shù).記

其中,h>0為充分大的正實(shí)數(shù).本文將考慮下述2種情況時(shí),方程(1)的對(duì)稱周期解問題:

當(dāng)考慮條件(τ1)的情況時(shí),為了滿足解的可延拓性,要求權(quán)函數(shù)q(t):R→R+為連續(xù)的有界變差函數(shù),且滿足:

(q0) 1) ?t∈[0,2π],q(t)≥0,且{t∈[0,ω]:q(t)>0}≠?;

2) 集合{t∈[0,2π]:q(t)≡0}只有有限個(gè)連通分支;

3) 若在(c,d)?[0,2π]上q>0且q(c)=0(或q(d)=0),則q在c的一個(gè)右鄰域內(nèi)單調(diào)不減(或相應(yīng)地q在d的一個(gè)左鄰域內(nèi)單調(diào)不增).

本文首先給出了證明方程(1)存在偶的周期解的一般性框架與偶的周期解存在的充分必要條件;其次,針對(duì)超線性條件(τ1),證明了方程(1)無窮多個(gè)偶的調(diào)和解的存在性;最后,針對(duì)次線性條件(τ2),證明了方程(1)無窮多個(gè)偶的次調(diào)和解的存在性.

2 引理

類似于文獻(xiàn)[3]中的做法,作變量代換

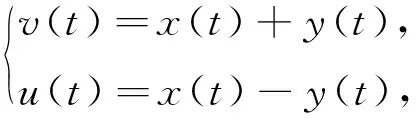
(3)

得方程(1)的等價(jià)系統(tǒng)

v″=h(t)+p(t),

(4)

u″+2q(t)g(u)=p(t)-h(t).

(5)

下面,分別研究方程(5)的偶周期解的存在性和重性問題.事實(shí)上,若方程(5)存在偶周期解u(t)且方程(4)存在偶周期解v(t),則易見

是方程(1)的偶的周期解.

下面,研究方程(1)存在偶周期解的條件.

引理2.1設(shè)(h0)成立,則方程(4)一定存在周期為2π的偶周期解.

證明設(shè)函數(shù)F(t)是h(t)+p(t)的一個(gè)原函數(shù),令

φ(t)=F(t)-F(0),

則顯然有φ′(t)=h(t)+p(t)且φ(0)=0.

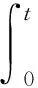
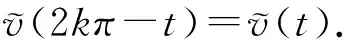
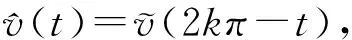
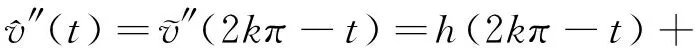
p(2kπ-t)=h(t)+p(t),

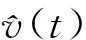
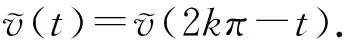
注意到

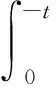
得

v′(-t)=-v′(t),

即

φ(-t)=-φ(t).

從而有

v′(-π)=-v′(π).

因?yàn)?/p>

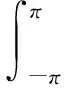
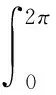
由(h0)知

v′(π)-v′(-π)=2v′(π)=0,

從而

v′(π)=v′(0)=0.

根據(jù)上述命題知

v(t)=v(-t)=v(t+2π).

得證.

推論2.1若方程(5)存在偶的調(diào)和解,則方程(1)一定存在偶的調(diào)和解(x(t),y(t)).

稱一個(gè)偶的周期解u(t)的初值點(diǎn)(u(0),u′(0))為一個(gè)ε-點(diǎn),由u的偶性可知u′(0)=0.特別地,若一個(gè)偶的周期解u(t)的最小周期為2mπ(m∈Z+),稱ε-點(diǎn)(u(0),u′(0))為m階的.

引理2.2[11]方程(5)的一個(gè)解u(t)是一個(gè)偶的周期解當(dāng)且僅當(dāng)存在一個(gè)正整數(shù)m,使u′(0)=u′(mπ)=0.特別地,這個(gè)ε-點(diǎn)(u(0),u′(0))為m階的當(dāng)且僅當(dāng)u′(0)=u′(mπ)=0且u′(kπ)≠0,k=1,2，…,m-1.

設(shè)對(duì)二維歐式空間R2中的每一個(gè)點(diǎn)q=(a,b)∈R2,定義

記u(t,a)為方程(5)在t=0時(shí)刻從(a,0)出發(fā)的解,a∈R.從引理2.1可知(a,0)是一個(gè)ε-點(diǎn)當(dāng)且僅當(dāng)存在某一個(gè)正整數(shù)m≥1使

u′(mπ)=0.

(6)

3 問題的轉(zhuǎn)化

考慮方程(5)的等價(jià)系統(tǒng)

(7)

其中，g1(u)=2g(u),e(t)=p(t)-h(t).

設(shè)連續(xù)截?cái)嗪瘮?shù)η:R2→R為

且滿足|η(u,w)|≤1.定義新的系統(tǒng)

(8)

在原點(diǎn)附近系統(tǒng)(8)為

u′=w,w′=-q(t)g1(u).

容易看出此時(shí)原點(diǎn)為該系統(tǒng)的平衡點(diǎn),由解的唯一性可知從原點(diǎn)外任一點(diǎn)出發(fā)的解都不會(huì)經(jīng)過原點(diǎn).在半徑為1的圓域之外,系統(tǒng)(8)為

u′=w,w′=-q(t)g1(u)+e(t).

顯然此時(shí)與原系統(tǒng)(7)一樣,從而系統(tǒng)(8)的任一滿足|(u(t),w(t))|>1的解都是原系統(tǒng)(7)的解.

設(shè)(u(t;u0,w0),w(t;u0,w0))為方程(8)滿足初值(u(0),w(0))=(u0,w0)的連續(xù)解.

引進(jìn)極坐標(biāo):假設(shè)(u0,w0)≠(0,0),則解(u(t;u0,w0),w(t;u0,w0))可以用極坐標(biāo)表示

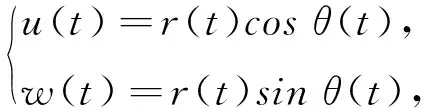
(9)

其中r(t)、θ(t)是連續(xù)函數(shù).易證,在坐標(biāo)變換(9)下,(r(t;r0,θ0),θ(t;r0,θ0))滿足方程

其中,u0=r0cosθ0,w0=r0sinθ0.

在下文中,為了討論方便,總假設(shè)對(duì)?R>R0,記(r(t,R),θ(t,R))為方程(10)的滿足r(0)=R,θ(0)=0(modπ)的解.

由u(t,a)的定義和方程(9)知,θ(t,a)是t的連續(xù)函數(shù)且可設(shè)θ(0,a)=0(因?yàn)閡′(0,a)=0).從方程(6)可知下述引理成立.

引理3.1(a,0)是一個(gè)ε-點(diǎn),即u(t,a)是一個(gè)偶的周期解當(dāng)且僅當(dāng)存在某個(gè)m≥1使得

θ(mπ,a)=0(modπ).

(11)

定義

為向量(u(t),w(t))在區(qū)間[t1,t2]上隨時(shí)間增加時(shí)在相平面上所轉(zhuǎn)的角度增量.易見,該值與θ(t)的選擇無關(guān).因此,方程(11)也可以表示為

θ(mπ,a)-θ(0,a)=lπ,l∈Z.

(12)

4 超線性方程

假設(shè)權(quán)函數(shù)q(t):R→R+為2π-周期連續(xù)的有界變差函數(shù)且滿足條件(q0).

類似于文獻(xiàn)[12]中的方法,可以證明下面的引理.

引理4.1假設(shè)(g0)和(q0)成立,任取(u0,w0)∈R2,則解(u(t;u0,w0),w(t;u0,w0))在(-∞,+∞)上有定義.

推論4.1對(duì)任一個(gè)L>0和α>0都存在一個(gè)常數(shù)β(α,L)>0,使

1) 若|(u0,w0)|≤α,則|(u(t),w(t))|≤β(α,L),對(duì)|t|≤L;

2) 若|(u0,w0)|>β(α,L),則|(u(t),w(t))|>α,對(duì)|t|≤L.

易證存在充分大的正數(shù)R*>0使得對(duì)任意的a>R*以及t∈(0,π],有θ(t,a)<0.

引理4.2[11]假設(shè)(g0)、(τ1)和(q0)成立,則對(duì)任意的正數(shù)H>0,都存在一個(gè)正數(shù)R=R(H)>R*,使得如果(r(t),θ(t))為方程(10)的定義在[a,b]上的一個(gè)解且滿足r(a)≥R,則有

θ(a)-θ(b)≥2πH.

引理4.3假設(shè)(g0)、(τ1)和(q0)成立,則方程(5)有無窮個(gè)偶的2π-周期解.

證明將證明分成以下兩步:第一步,從有關(guān)方程(11)的討論可知,我們的目標(biāo)是找到一列數(shù){ak},使得當(dāng)k→±∞時(shí)有ak→±∞且θ(π,ak)=0(modπ).因?yàn)閷?duì)于充分大的β>0來說,集合{θ(π,α);α>β}和{θ(π,α);α<-β}是連續(xù)的,所以,相應(yīng)地,只須證明

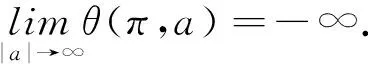
(13)

第二步，定義

表示從點(diǎn)(0,a)出發(fā)的解在區(qū)間[0,π]內(nèi)繞原點(diǎn)旋轉(zhuǎn)的圈數(shù),記

x(t,a)=x(t;0,(a,0)),

x′(t,a)=x′(t;0,(a,0)),

易見

rot[0,π](a):=

注意到e(t)是有界函數(shù),由推論4.1和引理4.2可得:當(dāng)|a|→+∞時(shí),對(duì)任意的t∈[0,π]都有

r(t,a)→+∞,

且

rot[0,π](a)→+∞.

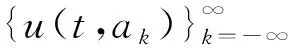
注4.1對(duì)充分大的β>0,若定義函數(shù)

Φ:[β,+∞)→R

則易證存在正數(shù)γ使得函數(shù)的值域?yàn)?/p>

Φ([β,+∞)):=(-∞,-γ].

由引理3.1和(12)式知,存在可數(shù)個(gè)al∈[β,+∞)滿足

θ(π,a)-θ(0,a)=lπ,l∈Z,

因此方程(5)有可數(shù)個(gè)偶的2π-周期解.

由引理4.3、引理2.1和推論2.1有定理4.1.

定理4.1假設(shè)(g0)、(τ1)和(q0)成立,則方程(1)有無窮多個(gè)偶的2π-周期解.

5 次線性方程

假設(shè)函數(shù)g(x):R→R滿足(g0)和(τ2).

引理5.1[13]存在正數(shù)R0>1,對(duì)(10)式的任意解(r(t),θ(t)),若r(t)>R0,則θ′(t)<0.

類似于文獻(xiàn)[14]中的方法,容易證明下述引理.

引理5.2假設(shè)(g0)和(τ2)成立,若(r(t),θ(t))是方程(10)的解滿足

r(t)≥R1≥R0, 0

和

θ(t2)-θ(t1)=-2π,

則

引理5.3[13]對(duì)每一個(gè)R>R0和每一個(gè)j>0,都存在L(R,j)>R使得如果(r(t),θ(t))是方程(10)的解滿足r(t1)=L(R,j),r(t2)=R(或者r(t1)=R,r(t2)=L(R,j))及

R≤r(t)≤L(R,j), ?t∈[t1,t2],

則

θ(t2)-θ(t1)<-2jπ.

另一方面,由θ′的連續(xù)性易證下述引理.

引理5.4設(shè)R2>R1>R0是充分大的正數(shù),(r(t),θ(t))是(10)式的一個(gè)解滿足

R1≤r(t)≤R2, ?t≥0,

則

θ(t)-θ(0)→-∞,t→+∞.

定理5.1假設(shè)(g0)、(τ2),則方程(5)有無窮個(gè)偶的次調(diào)和解.

θ(mπ)-θ(0)<-2jπ.

1) 或者(u(t),v(t))∈Aj,?t∈[0,mπ],其中(u(t),v(t))由(9)式給出;

θ(mπ)-θ(0)<-2jπ.

以及

[1] TORRES P J, ZANOLIN F. Periodic motion of a system of two or there charged particles[J]. J Math Anal Appl,2000,250(2):375-386.

[2] TORRES P J. Periodic motions forced infinite lattices with nearest neighbor interaction[J]. Z Angew Math Phys,2000,51(3):333-345.

[3] TORRES P J. Necessary and sufficient conditions for existences of periodic motions of forced systems of particles[J]. Z Angew Math Phys,2001,52(3):535-540.

[4] SUN J, MA S. Nontrivial periodic motions for resonant type asymptotically linear lattice dynamical systems[J]. J Math Anal Appl,2014,417(2):622-634.

[5] WANG C, QIAN D. Periodic motions of a class of forced infinite lattices with nearest neighbor interaction[J]. J Math Anal Appl,2008,340(1):44-52.

[7] GENDELMAN O. Exact solutions for discrete breathers in a forced-damped chain[J]. Physical Review E:Statistical Nonlinear & Soft Matter Physics,2013,87(6):062911.

[8] LIU Z, GUO S, ZHANG Z. Existence of homoclinic travelling waves in infinite lattices[J]. Bulletin of the Malaysian Mathematicalences Society,2013,36(4):965-983.

[9] ZHOU S F, HAN X Y. Pullback exponential attractors for non-autonomous lattice systems[J]. J Dynamics and Differential Equations,2012,24(3):601-631.

[11] 王超. 一類帶正權(quán)超線性對(duì)稱方程對(duì)稱周期解的分布[J]. 四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2011,34(6):844-849.

[12] PAPINI D. Boundary value problems for second order differential equations with superlinear terms:a topological approach[D]. Trrieste:Scuola Internazionale Superiore di Studi Avanzati,2000.

[13] 楊瀟,周鑫,楊曉燕,等. 一類次線性雙質(zhì)子耦合格點(diǎn)系統(tǒng)的周期解[J]. 四川師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2016,39(2):236-241.

[14] DING T, ZANOLIN F. Subharmonic solution of second order nonlinear equations:a time-map approach[J]. Nonlinear Analysis Theory Methods & Applications,1993,20(5):509-532.

[15] FABRY C, HABETS P. Periodic solutions of second order differential equations with superlinear asymmetric nonlinearities[J]. Arch Math,1993,60(3):266-276.

[16] PAPINI D, ZANOLIN F. Differential equations with indefinite weight:boundary value problems and qualitative problems of the solutions[J]. Rendiconti Del Seminario Matematico,2003,60(4):265-295.