實序線性空間中集值優化ε-Henig真有效元二階復合切上圖導數的最優性條件

余 麗

(宜春學院 數學與計算機科學學院和應用數學研究中心, 江西 宜春 336000)

近年來,用二階切導數刻畫集值優化問題最優性條件取得了突破性的成果[1-4].Aubin等[1]引進的二階切集,在建立二階最優性條件中起著重要作用.Jahn等[2]引進了廣義二階切上圖導數并建立了二階最優性條件.然而,該廣義二階切上圖導數是借助二階切集定義的,二階切集僅為閉集,通常情況下并不是錐,即使是凸集,它的二階切集也不一定為凸集.因而,與切上圖導數相比較,廣義二階切上圖導數不具備一些類似性質.為克服此問題,Zhu等[4]引進了一種新的二階切上圖導數——二階復合切上圖導數(second-order compound contingent epiderivative),并在一定條件下建立了存在性定理,證明了該導數是嚴格正齊次和次可加的,同時,借助該導數得到了集值優化問題局部弱有效元的二階必要最優性條件.另一方面,有效解是集值優化的重要組成部分,對有效解的研究已經取得了豐碩的成果[5-7].然而,對有效解的研究大多局限在拓撲空間,目前為止,只有少量文獻在線性空間中研究集值優化問題有效解的最優性條件[8-10].眾所周知,線性空間是比拓撲空間更大的空間,為此,在線性空間中研究集值優化問題最優性條件顯得尤為重要.本文利用二階復合切上圖導數,在實序線性空間中建立集值優化問題ε-Henig真有效元的二階最優性條件.由于逼近解結構中含有ε,為此,定理的結構在形式上與文獻[4]略有不同.與此同時,證明方法上也有很大的差別:除了借助二階復合切上圖導數的概念外,還利用了基函數和均衡吸收凸集的性質,并結合反證法得到了相關結論.文獻[4]的結論不包含本文結論,本文推廣了文獻[2-3]的相關結論.

1 基本概念及有關結論

設X、Y為實序線性空間,?≠K?Y,K的生成錐定義為cone K:={λk:k∈K,λ≥0}.K稱為凸錐當且僅當λ1k1+λ2k2∈K,?λ1,λ2≥0,?k1,k2∈K.錐K稱為點的當且僅當K∩(-K)={0}.K稱為非平凡的當且僅當K≠{0}且K≠Y.用intK和clK表示K的內部和閉包.設C?Y為非平凡的點閉凸錐,且intC≠?.設F:X→2Y為集值映射,F的域、圖和上圖分別定義為:

domF:={x∈X|F(x)≠?},graphF:={(x,y)∈X×Y|y∈F(x)},epiF:={(x,y)∈X×Y|y∈F(x)+C}.

定義1.1[11]設B為Y中的非空凸子集,B稱為C的基當且僅當C=coneB,且存在一均衡吸收的凸集V使得0?B+V.

記Bst:={y*∈Y*:存在t>0,使得y*(b)≥t,?b∈B}.以下假設B是C的基,設V?Y是均衡吸收的凸集,滿足0?B+V.記CV(B):=cone(B+V).易知CV(B)是非平凡的點凸錐且0?cor(CV(B)).

定義1.3[12]設?≠K?Y,K的代數內部定義為

corK:={k∈K|?k′∈Y,?λ′>0,

?λ∈[0,λ′],k+λk′∈K}.

定義1.4[13]設?≠K?Y,K稱為均衡的當且僅當?k∈K,?λ∈[-1,1],有λk∈K.K稱為吸收的當且僅當0∈corK.

注1.1[11]由定義1.3和定義1.4知,非空集合K稱為吸收的當且僅當?y∈Y,?λ′>0,?λ∈[0,λ′],有λy∈K.

?tn↓0,

或等價于

?λn→+∞,

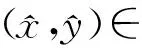
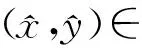
2 最優性條件

考慮下面的集值優化問題：

(P)minF(x)

s.t.x∈S,

其中,?≠S?X,F:S→2Y為集值映射.

?

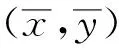
(1)

即

(3)

于是

由定義1.7有

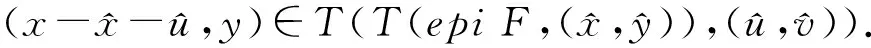
(4)

因為

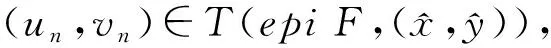
由(3)和(4)式知

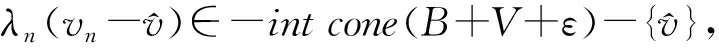
即

?n≥N2.

(7)

于是由(6)和(7)式知,?n≥max(N1,N2),有

-intcone(B+V+ε)-C?

-intcone(B+V+ε).

(8)

并且由(5)式有

結合(8)式,?n∈N,n≥max(N1,N2),存在K1(n)∈N使得

即

?n≥max(N1,N2), ?k≥K1(n).

(9)

結合(9)式,有?n≥max(N1,N2),?k≥K1(n),有

?-intcone(B+

V+ε)-C?-intcone(B+V+ε),

于是

(10)

下面證明

先證明0?intcone(-B-V-ε).反證法.若

0∈intcone(-B-V-ε),

則由cone(-B-V-ε)為凸集知

intcone(-B-V-ε)=intclcone(-B-V-ε).

因為0∈intclcone(-B-V-ε),所以

clcone(-B-V-ε)=Y.

任取b∈B?Y,則存在{tλ(-bλ-vλ-ε):λ∈Λ}使得tλ(-bλ-vλ-ε)→b,其中tλ≥0,bλ∈B,vλ∈V.因為ε∈C,則存在b1∈B,λ1≥0,使得ε=λ1b1,于是

tλ(-bλ-vλ-λ1b1)-b→0.

因為0?B+V,于是存在λ0∈Λ,bλ0∈B,Vλ0∈V使得

tλ(-bλ-vλ-λ1b1-b)=bλ0+vλ0,

于是

-tλvλ-vλ0=bλ0+tλbλ+tλλ1b1+tλb.

兩邊同時除以2tλ+tλλ1+1得

因為V是均衡吸收凸的,有

?V,

所以

由B是C的有界基及文獻[15]中命題2.1知存在t>0使得Bst≠?.設φ∈Bst,于是有φ(b)≥t,?b∈B.于是

此與(12)式矛盾.于是

0?intcone(-B-V-ε).

(13)

由(10)式知存在

從而

y*∈intcone(-B-V-ε)?cone(-B-V-ε).

由(13)式得y*≠?,于是存在λ2>0,b2∈B,v2∈V,使得

y*=λ2(-b2-v2-ε),

所以

結合(14)式有

即

因為-(b2+v2)≠0,于是

-b2-v2∈-(B+V)?-cone(B+V){0},

所以

?,

即

?.

此與(2)式矛盾.故(1)式成立.

[1] AUBIN J P, FRANKOWSKA H. Set-valued Analysis[M]. Boston:Birkhauser,1990.

[2] JAHN J, KHAN A A, ZEILINGER P. Second-order optimality conditions in set optimization[J]. J Optim Theory Appl,2005,125(2):331-347.

[3] LI S J, ZHU S K, TEO K L. New generalized second-order contingent epiderivatives and set-valued optimization problems[J]. J Optim Theory Appl,2012,152(3):587-604.

[4] ZHU S K, LI S J. New second-order contingent epiderivatives and set-valued optimization problems[J]. Acta Math Appl Sin,2016,32(4):983-994.

[5] LI Z F. Benson proper efficiency in the vector optimization of set-valued maps[J]. J Optim Theory Appl,1998,98(3):623-649.

[6] QIU Q S. Henig efficiency in vector optimization with nearly cone-subconvexlike set-valued functions[J]. Acta Math Appl Sin,2007,23(2):319-328.

[7] LI T Y, XU Y H, ZHU C X.ε-Strictly efficient solutions of vector optimization problems with set-valued maps[J]. Asia Pacific J Oper Res,2007,24(6):841-854.

[8] HERNANDEZ E, JIMENEZ B, NOVO V. Weak and proper efficiency in set-valued optimization on real linear spaces[J]. J Convex Anal,2007,14(3):275-296.

[9] HERNANDEZ E, JIMENEZ B, NOVO V. Benson proper efficiency in set-valued optimization on real linear spaces[J]. Lect Notes Econ Math Syst,2006,563(2):45-59.

[10] ZHOU Z A, PENG J W. Scalarization of set-valued optimization problems with generalized cone subconvexlikeness in real ordered linear spaces[J]. J Optim Theory Appl,2012,154(3):830-841.

[11] ZHOU Z A, YANG X M.ε-Henig proper efficiency of set-valued optimization problems in real ordered linear spaces[J]. Optim Lett,2014,8(6):1813-1827.

[12] JAHN J. Vector Optimization:Theory, Methods, and Application to Design Problems in Engineering[M]. 2nd ed. Berlin:Springer-Valerg,2011.

[13] 史樹中. 凸分析[M]. 上海:上海科學技術出版社,1990.

[14] JAHN J, RAUH R. Contingent epiderivatives and set-valued optimization[J]. Math Meth Oper Res,1997,46(2):193-211.

[15] CHENG Y H, FU W T. Strong efficiency in a locally convex space[J]. Mathematical Methods of Operations Research,1999,50(3):373-384.