超歐拉和雙有向跡的強積有向圖

崔秋月, 劉 娟, 董暢暢

(新疆師范大學 數(shù)學科學學院, 新疆 烏魯木齊 830017)

下面介紹了強積有向圖的定義.

定義1令D1=(V1,A1)和D2=(V2,A2)是2個有向圖,V1={u1,u2,…,un1},V2={v1,v2,…,vn2},則D1和D2的強積有向圖定義如下:強積有向圖記作D1?D2,其點集為V1×V2,任意2個不同的點(ui,vj)和(us,vt),若((ui,vj),(us,vt))∈A(D1?D2)當且僅當以下3個條件之一成立:

1)ui=us且(vj,vt)∈A2;

2)vj=vt且(ui,us)∈A1;

3) (ui,us)∈A1且(vj,vt)∈A2.

Boesch等[3]在1977年提出了超歐拉問題,他們致力于刻畫出包含生成歐拉子圖的無向圖,同時,他們表示這個問題是非常困難的.Pulleyblank[4]在1979年證明了判定一個無向圖(甚至包含平面無向圖)是否是超歐拉的條件是NP-完備性.截至今日,已經(jīng)有大量關于超歐拉無向圖的研究,例如Catlin的研究[5]和文獻[6-7].

在文獻[13]中,一個開放性的問題(問題6)被提出,關于尋找使得無向圖的積圖成為哈密爾頓圖的條件.受此問題的啟發(fā),本文提出尋找使得2個有向圖的積圖成為超歐拉有向圖的條件.文獻[14]研究了對于給定直徑，有向圖超歐拉的充分條件.本文將研究關于2個有向圖的強積圖成為超歐拉有向圖或雙有向跡有向圖的充分條件.

1 符號

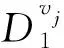
命題1.1令D1=(V1,A1)和D2=(V2,A2)是兩個有向圖,V1={u1,u2,…,un1},V2={v1,v2,…,vn2},則下面的每一條都成立:

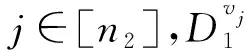
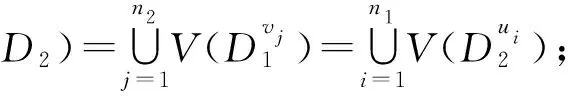
2 強積有向圖

下面介紹的引理2.1將被應用在證明一個有向圖是非超歐拉有向圖的例子上.

引理2.1[15]對于某個正整數(shù)m和一個有向圖D,如果V(D)包含點不交的子集B,B1,…,Bm且滿足以下2個條件:

1)N-(Bi)?B,i∈[m];

2) |?-(B)|≤m-1,

則稱D是非超歐拉有向圖.

下面將介紹2個有向圖D1和D2的強積有向圖D1?D2成為超歐拉有向圖的充分條件.

定理2.2令D1是超歐拉有向圖且|V(D1)|≥2,D2是強連通有向跡的,則強積有向圖D1?D2是超歐拉有向圖.

證明令V(D1)={u1,u2,…,un1},V(D2)={v1,v2,…,vn2}且ui1=u1,vj1=v1.如果|V(D2)|=1,則D1?D2?D1是超歐拉有向圖.因此,假設|V(D2)|≥2.因為D1是超歐拉有向圖,令H1是D1中弧數(shù)最少的生成有向閉跡且

H1=ui1ui2…uih1ui1, i1,i2,…,ih1∈[n1].(1)

因為D2是有向跡的,令H2是D2中從vj1到vjh2弧數(shù)最少的生成有向跡且

H2=vj1vj2…vjh2,j1,j2,…,jh2∈[n2].

(2)

根據(jù)(1)式有(uih1,ui1)∈A(D1).對于任意2個相鄰的點vr-1,vr∈V(D2),2≤r≤n2,如果(vr-1,vr)∈A(D2),根據(jù)強積有向圖的定義,則有

((uih1,vr-1),(ui1,vr))∈A(D1?D2).

(3)

因為D2是強連通的,所以D2包含一個最短(vjh2,vj1)-有向路P=vjskvjsk-1…vjs2vjs1,vjsk=vjh2且vjs1=vj1.

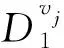
算法A

輸出D1?D2中起點為(ui1,vj1)的生成有向閉跡H.

2) 如果p>q,令H:=H+((uih1,vjh2),(ui1,vjh2))∪P′,執(zhí)行第5步.

3) 令H是當前的有向跡且終點為(uih1,vjr-1).

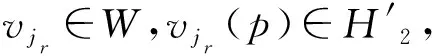
5) 返回有向跡H.

下面的例2.3介紹了一個超歐拉有向圖和一個強連通但不是有向跡有向圖,使得它們的強積有向圖D1?D2是非超歐拉有向圖.

例2.3令D1是超歐拉有向圖,其點集為V(D1)={u1,u2},弧集為A(D1)={(u1,u2),(u2,u1)},則D1?C2.令D2是強連通有向圖,其點集為V(D2)={v1,v2,v3,v4,v5,v6,v7},弧集為A(D2)={(v2,v1),(v1,v3),(v3,v2),(v1,v4),(v4,v2),(v1,v5),(v5,v2),(v1,v6),(v6,v2),(v1v7),(v7,v2)}.因為D2不包含生成有向跡,所以D2不是有向跡有向圖.根據(jù)定義1,可以得到D1和D2的強積有向圖D1?D2(如圖1所示).令B、B1、B2、B3、B4和B5是V(D1?D2)的點不交的子集,其中,B={(u1,v1),(u2,v1)},B1={(u1,v3),(u2,v3)},B2={(u1,v4),(u2,v4)},B3={(u1,v5),(u2,v5)},B4={(u1,v6),(u2,v6)}和B5={(u1,v7),(u2,v7)}.可以發(fā)現(xiàn)N-(Bi)?B,i∈[5]且|?-(B)|=4.根據(jù)引理2.1,強積有向圖D1?D2是非超歐拉有向圖.

例2.3表明存在有向圖D1,|V(D1)|=2和D2,|V(D2)|=7,則強積有向圖D1?D2是非超歐拉有向圖.事實上,對于n1,n2∈N,n2≤2n1+3,例2.3可以推廣到一般的情況:令D1是一個有向圈,其點集為V(D1)={u1,u2,…,un1},D2是一個強連通有向圖,其點集為V(D2)={v1,v2,…,vn2},弧集為A(D2)={(v2,v1),(v1,v3),(v3,v2),(v1,v4),(v4,v2),…,(v1,vn2),(vn2,v2)}.令B,B1,B2,…,Bn2-2是V(D1?D2)的點不交的子集,其中B={(u1,v1),(u2,v1),…,(un1,v1)},Bi={(u1,vi+2),(u2,vi+2),…,(un1,vi+2)},i∈[n2-2].可以發(fā)現(xiàn)N-(Bi)?B,i∈[n2-2]且|?-(B)|=2n1≤n2-3=(n2-2)-1.根據(jù)引理2.1,強積有向圖D1?D2是非超歐拉有向圖,見圖1,其中弧((u1,v1),(u2,vj)),((u2,v1),(u1,vj)),((u1,vj),(u2,v2))及((u2,vj),(u1,v2))被省略,j={3,4,5,6,7}.

圖 1 有向圖D1,D2和強積有向圖D1?D2

下面的例2.4介紹了一個強連通有向跡有向圖和一個強連通但不是有向跡有向圖,使得它們的強積有向圖D1?D2是非超歐拉有向圖.

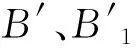
通過例2.3和例2.4可以說明定理1.2中的條件是最優(yōu)的.

下面將介紹2個有向圖D1和D2的強積有向圖D1?D2成為雙有向跡有向圖的充分條件.

圖2有向圖D1和D2

Fig.2DigraphsofD1andD2

定理2.5令D1和D2是2個雙有向跡有向圖,則強積有向圖D1?D2是雙有向跡有向圖.

證明令V(D1)={u1,u2,…,un1},V(D2)={v1,v2,…,vn2}.如果|V(D1)|=1,則D1?D2?D2是雙有向跡有向圖.如果|V(D2)|=1,則D1?D2?D1是雙有向跡有向圖.因此,假設|V(Di)|≥2,i=1,2.因為D1是雙有向跡有向圖,所以D1中存在一對不同的點x1,y1使得D1包含生成(x1,y1)-有向跡H11和生成(y1,x1)-有向跡H12,令

H11=usul1ul2…ulh1ut,

H12=utum1um2…umh1us,

(4)

x1=us,y1=ut,s,t,l1,l2,…,lh1,m1,m2,…,mh1∈[n1].令H11是D1中從us到ut弧數(shù)最少的生成有向跡,H12是D1中從ut到us弧數(shù)最少的生成有向跡.

類似地,因為D2是雙有向跡有向圖,所以D2中存在一對不同的點x2、y2使得D2包含生成(x2,y2)-有向跡H21和生成(y2,x2)-有向跡H22,令

H21=vi1vi2…vih2,H22=vj1vj2…vjh2,

(5)

x2=vi1=vjh2,y2=vih2=vj1,i1,i2,…,ih2,j1,j2,…,jh2∈[n2].令H21是D2中從vi1到vih2弧數(shù)最少的生成有向跡,H22是D2中從vj1到vjh2弧數(shù)最少的生成有向跡.

對于任意2個相鄰的點vr-1,vr∈V(D2),2≤r≤n2,如果(vr-1,vr)∈A(D2),根據(jù)強積有向圖的定義有

((us,vr-1),(us,vr))∈A(D1?D2),

((ut,vr-1),(ut,vr))∈A(D1?D2).

(6)

如果|V(D2)|是奇數(shù),H1的終點為(ut,vih2),則可以利用上面的過程得到從點(ut,vj1)到點(us,vjh2)的生成有向跡H2;如果|V(D2)|是偶數(shù),H1的終點為(us,vih2),則可以利用上面的過程得到從點(us,vj1)到點(us,vjh2)的生成有向跡H2.最終得到D1?D2中的生成(y,x)-有向跡H2.

算法B

輸出D1?D2中起點為(us,vi1)的生成有向跡H1.

2) 如果p>q,執(zhí)行第6步.

3) 令H1是當前的有向跡.

如果(ut,vir-1)為H1的終點,執(zhí)行第4步.

如果(us,vir-1)為H1的終點,執(zhí)行第5步.

6) 返回有向跡H1.

致謝新疆師范大學“十三五”校級重點學科數(shù)學招標課題(17SDKD1107)和新疆師范大學碩士研究生科技創(chuàng)新項目(XSY201602013)對本文給予了資助，謹致謝意.

[1] BONDY J A, MURTY U S R. Graph Theory[M]. New York:Springer-Verlag,2008.

[2] BANG-JENSEN J, GUTIN G. Digraphs:Theory Algorithms and Applications[M]. 2nd ed. New York:Springer-Verlag,2010.

[3] BOESCH F T, SUFFEL C, TINDELL R. The spanning subgraphs of Eulerian graphs[J]. J Graph Theory,1977,1(1):79-84.

[4] PULLEYBLANK W R. A note on graphs spanned by Eulerian graphs[J]. J Graph Theory,1979,3(3):309-310.

[5] CATLIN P A. Supereulerian graphs:a survey[J]. J Graph Theory,1992,16(2):177-196.

[6] CHEN Z H, LAI H J. Reduction techniques for super-Eulerian graphs and related topics:a survey[C]//Combinatorics and Graph Theory. New Jersey:World Science Citation Index Publishing,1995:53-69.

[7] LAI H J, SHAO Y, YAN H. An update on supereulerian graphs[J]. World Scientific and Engineering Academy Society Transactions on Mathematics,2013,12(9):926-940.

[8] GUTIN G. Cycles and paths in directed graphs[D]. Tel Aviv:Tel Aviv University,1993.

[9] GUTIN G. Connected (g;f)-factors and supereulerian digraphs[J]. Ars Combinatoria,2000,52:311-317.

[10] ALGEFARI M J, ALSATAMI K A, LAI H J, et al. Supereulerian digraphs with given local structures[J]. Information Processing Letters,2016,116(5):321-326.

[11] BANG-JENSEN J, MADDALONI A. Sufficient conditions for a digraph to be supereulerian[J]. J Graph Theory,2015,79(1):8-20.

[12] HONG Y, LAI H J, LIU Q. Supereulerian digraphs[J]. Discrete Mathematics,2014,330:87-95.

[13] GOULD R J. Advances on the Hamiltonian problem:a survey[J]. Graphs and Combinatorics,2003,19:7-52.

[14] DONG C, LIU J, ZHANG X, et al. Supereulerian digraphs with given diameter[J]. Appl Math Comput,2018,329:5-13.

[15] ALSATAMI K A, ZHANG X D, LIU J, et al. On a class of supereulerian digraphs[J]. Appl Math,2016,7(3):320-326.