有界區間上的隨機非局部Ginzburg-Landau方程

何 興, 陳光淦

(1. 四川大學 錦江學院, 四川 彭山 620860; 2. 四川師范大學 數學與軟件科學學院, 四川 成都 610066)

1 引言及預備知識

分數階微分方程包括分數階微分和分數階積分,不但有深淵的物理背景,而且其應用也相當廣泛,如混沌動力學[1]、復動力系統[2]等.近十多年來,分數階微分方程在流體力學、材料力學等領域得到深入研究,包括分數階p-Laplace方程[3]、分數階Schr?dinger方程[4]、分數階Landau-Lifshitz方程[5]、分數階Landau-Lifshitz-Maxwell方程[6],以及分數階Ginzburg-Landau方程[7]等.

本文在有界區間上考慮帶乘性噪聲的非局部Ginzburg-Landau方程

(1)

其中,t∈[0,T],D=(-1,1),Dc=RD,i為虛數單位,μ、ν、r>0,σ>0為實常數,W(t)是維納過程.非局部Laplace算子(-Δ)α定義為

(2)

其中,x∈D,Cα是與α有關的常數.

文獻[8]中定義在整個實數空間R上的分數階Laplace算子(-Δ)α,它是一個微分算子,可以通過傅立葉級數來定義,由此定義出經典的分數階Sobolev空間.而本文中出現的分數階Laplace算子(-Δ)α是定義在一個有界區間D上.由于是一個非局部Laplace算子,經典的分數階Sobolev空間不適用,因此需要定義一個加權非局部Sobolev空間.更多關于在有界區間上的非局部Laplace算子的信息,詳見文獻[9-10].

定義1.1[11]設α∈(0,1),D?R,定義分數階Sobolev空間

L2(D×D)},

其范數為

其中

被稱為u的半范數.

引理1.1[11]令α∈(0,1),D是R上的有界區間,則存在常數C=C(α,D),使得對任意的u∈L2(D)有

‖u‖C0,β(D)≤C‖u‖Wα,2(D),

本文考慮D=(-1,1)?R,由文獻[11]有

再根據文獻[12],設ν(x,y),β(x,y):R×R→Rk,其中β滿足β(x,y)=-β(y,x),且

顯然D(ν):R→R.給定映射u(x):R→R,D*表示D的伴隨算子,則

D*(u)(x,y)=(u(x)-u(y))β(x,y),x,y∈R,

顯然

D*(u):R×R→Rk.

用Θ(x,y)=Θ(y,x)表示二階張量,且滿足Θ=ΘT,那么有

β(x,y)·(Θ(x,y)·β(x,y))dy,

其中x∈R,D(Θ·D*u):R→R.當Θ為單位矩陣時,同時β滿足

則

其中

從而有

D(Θ·D*u)(x).

(4)

由(4)式表明經典的分數階Sobolev空間Wα,2(D)在這不適用,因不能保證

定義

Hα(R)={u∈L2(R):

則

其范數為

引理1.2[13]設B0、B、B1均為Banach空間,且B0和B1是自反的,B0?B?B1,同時B0緊嵌入到B,γ∈(0,1),X=L2(0,T;B0)∩Wγ,2(0,T;B1),則X緊嵌入到L2(0,T;B).

2 鞅解的存在性

下設

則有

再設W(t)是一個完備概率空間(Ω,F,P)上的維納過程,且在可分的Hilbert空間U上取值.算子Q是定義在U上的非負對稱算子,滿足TrQ<+∞,則在U上存在一個完備的標準正交基{ei}i≥1和非負的有界實值序列λi,使得Qei=λiei且

于是

其中βi(t)是相互獨立的維納過程.記L2(U,H)是從U到H的全體有界線性算子組成的空間,則對任意的G∈L2(U,H)有

進一步假設(A)：g:H→L2(U,H)是連續的,且滿足

其中,u、v∈H,參數C、λ為正實數.

顯然Pn|H是H到Hn的正交投影,且對?u∈Vα,υ∈Hn可得

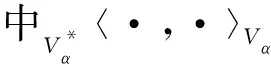
由于在有限維空間上的隨機微分方程滿足Lipschitz和線性增長條件,則方程(5)存在唯一解

第二步,先驗估計.令

取期望得

再由Gronwall不等式得

(6)

(7)

再令

再由Burkholder-Davis-Gundy不等式和Young不等式可得

最后由Gronwall不等式得

(8)

I1+I2(t)+I3(t)+I4(t)+I5(t).

(9)

由(6)式可得

同理可證

(10)

因為

于是取φ∈Vδ,則

|〈un,(-Δ)αφ〉H|≤

‖un‖H‖(-Δ)αφ‖H.

(-Δ)αφ(x)=

于是有

同理可證

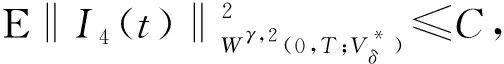
(11)

因為

由G-N不等式以及Young不等式可得

同理可證

(12)

因為

同理可證

下面利用文獻[14-15]的方法證明鞅解.記

則

顯然Mn(t)是一個鞅,且E‖Mn(t)‖2<+∞.再令φ是空間L2(0,T;H)里的一個連續有界復值函數且0≤s≤t≤T.因為Mn(t)是濾子為σ{un(s):0≤s≤t}的鞅,則

E([Mn(t)-Mn(s)]φ(un(·)))=0,

(13)

以及對所有的a、b∈H有

E([〈Mn(t),a〉〈Mn(t),b〉-

〈Mn(s),a〉〈Mn(s),b〉-

φ(un(·)))=0.

(14)

再記

因為

則

所以有

(15)

(16)

對應的二階變差為

對(15)和(16)式取極限可以得到

(17)

以及

(18)

其中

令(-Δ)α=A,則

對應的二階變差為

最后由鞅表示定理可得方程(1)存在一個鞅解.

[1] ZASLAVSKY G M. Chaos, fractional kinetics, and anomalous transport[J]. Physics Reports,2002,371(6):461-580.

[2] NIGMATULLIN R R. The realization of the generalized transfer equation in a medium with fractal geometry[J]. Physica Status Solidi,1986,133(1):425-430.

[3] 湯小松,羅節英. 一類分數階p-Laplace方程積分三點邊值問題正解的存在性[J]. 四川師范大學學報(自然科學版),2014,37(6):867-874.

[4] GUO B L, HUO Z. Global well-posedness for the fractional nonlinear Schr?dinger equation[J]. Communication in Partial Differential Equations,2010,36(2):247-255.

[5] GUO B L, ZENG M. Solution for the fractional Landau-Lifshitz equation[J]. J Math Anal Appl,2010,361(1):131-138.

[6] PU X K, GUO B L. Global weak solution of the fractional Landau-Lifshitz-Maxwell equation[J]. J Math Anal Appl,2010,372(1):86-98.

[7] VASILY E T, GEORGE M Z. Fractional Ginzburg-Landau equation for fractal media[J]. Physica,2005,A354(1):249-261.

[8] LU H, Lü S J. Random attracor for fractional Ginzburg-Landau equantion with multiplicative noise[J]. Taiwanese J Mathematics,2014,18(2):435-450.

[9] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. Analysis and approximation of nonlocal diffusion problems with volume constraints[J]. SIAM Rev,2012,54(4):667-696.

[10] CHEN Z Q, MEERSCHAERT M M, NANE E. Space-time fractional diffusion on bounded domains[J]. J Math Anal Appl,2012,393(2):479-488.

[11] NEZZA E D, PALATUCCI G, VALDINOCI E. Hitchhiker’s guide to the fractional Sobolev spaces[J]. Bull Sci Math,2011,136(5):521-573.

[12] DU Q, GUNZBURGER M, LEHOUCQ R B, et al. A nonlocal vector calculus, nonlocal volume-constrained problems, and nonlocal balance laws[J]. Mathematical Models & Methods in Applied Sciences,2013,23(3):493-540.

[13] FLANDOLI F, GATAREK D. Maitingale and stationary solutions for stochastic Navier-Stokes equations[J]. Probability Theory & Related Fields,1995,102(3):367-391.

[14] DA PRATO G, ZABCZYK J. Stochastic Equations in Infinite Dimensions[M]. Cambridge:Cambridge University Press,1992.

[15] BRZEZNIAK Z, MOTYL E. Existence of a martingale solution of the stochastic Navier-Stokes equations in unbounded 2Dand 3Ddomains[J]. J Differential Equations,2013,254(4):1627-1685.