習題教學中落地數學核心素養*
——圓錐曲線二輪復習的教學與反思

●

(鎮海中學,浙江 寧波 315200)

在二輪復習的課堂中，提高習題教學的質量非常重要.《普通高中數學課程標準(2017版)》指明了構建高效課堂的方式：把握數學本質、啟發思考、改進教學.

美國數學家哈爾莫斯曾說過：問題是數學的心臟.因此，在習題教學中應注重選擇合適的問題，引領復習方向，承載復習內容，通過抓住問題的本質，建立知識之間的關聯，達到加強學生的解題能力、提升學生的數學思維能力之目標.習題教學的效率某種程度上決定著高考復習質量的高低，影響著高考的成敗.但在習題教學的具體實踐中，還是有不少教師信奉“題海戰術”兼灌輸式講授，這樣非但不能提升學生的解題能力，久而久之還會挫傷學生的學習積極性，使學生產生厭學情緒，出現簡單題不肯做、難題又不會做的情況.

筆者一直在探尋高效的習題教學之路，讓學生能在潛移默化中提升數學核心素養.本文以二輪復習中”圓錐曲線復習課“為例，談談如何滲透數學核心素養，提升學生的思維能力，杜絕學生在解題中出現“只會埋頭拉車，卻不抬頭看路”的糟糕現象.

1 教學過程

1.1 復習回顧

師：同學們經歷了圓錐曲線的一輪復習，也做了不少題目，大家到底學了哪些知識？

(學生各抒己見，教師進行總結.)

師：我們學到的知識有：1)曲線分類;2)曲線的性質;3)性質應用.基本的研究思想是用代數研究幾何，而最常用的方法是設點法和設線法，并借助韋達定理解決問題.我們不僅可以從定義上區分曲線，還可以從曲線的性質上加以區分.比如教材中提到的光學性質，該性質有怎樣的幾何特征？

設計說明在復習回顧中，與學生一起梳理圓錐曲線的知識結構與體系，厘清基本思想與常用方法，掌握概念的內涵和外延，使知識的展開不再是無源之水、無本之木，提高習題教學的效率，同時發展學生數學抽象的核心素養，引領學生學會學習，養成良好的學習習慣.

生1:從橢圓一個焦點出發的光線經反射后聚焦于另一個焦點，而雙曲線反射后發散，其反向延長線過另一個焦點，經拋物線反射后平行射出.

師：這些性質均與焦點有關，體現了圓錐曲線的統一美，但它們也有差異性，分別為聚焦、發散、平行.再看它們的這些反射面，表現為圓錐曲線的切線，那么這些切線又有怎樣的性質呢？

生2:由曲線外的某定直線(準線)上一點出發引曲線的兩條切線，則切點弦必過定點(對應焦點)，反之亦成立.

師：這個性質在圖形中的體現非常優美，因此同學們留下了較深的印象.我們對這類性質的理解越深、對圖形的分析越透，對我們的解題就越有幫助.

1.2 引例示范

例1已知拋物線C的方程為x2=4y，F為其焦點，過不在拋物線上的一點P作此拋物線的切線PA，PB，點A，B為切點，且PA⊥PB.

1)求證：直線AB過定點；

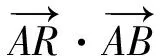
(2018年浙江省寧波市高三數學期末試題第21題)

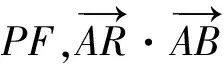
生3:可以先求出點R的坐標，然后進行表示.

師：直譯目標，但不簡便，能否簡化問題？

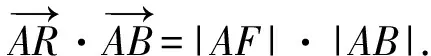
師：很好！還能進一步簡化嗎？

生5:由PA⊥PB，PF⊥AB，根據射影定理可轉化成|PA|2.

師：非常好！抓住圖形的幾何特征，回歸問題的本質，將問題轉化成更簡單的形式：過拋物線x2=4y上一點A作切線與準線y=-1交于點P，求|PA|2的最小值.有了知識的沉淀，學會欣賞圖形之美，就可以啟發我們思考，引領解題方向.

設計說明以學生考過且不理想的問題作引例，不僅能拉近與學生的距離，還能引起學生的共鳴，從而啟發解題思考，轉化問題，簡化運算，提高解題效率.同時突出主題，注重幾何圖形對解題的引領作用，在解題中遇到瓶頸之時，應當回歸本質，分析圖形，獲取思路，突破瓶頸.

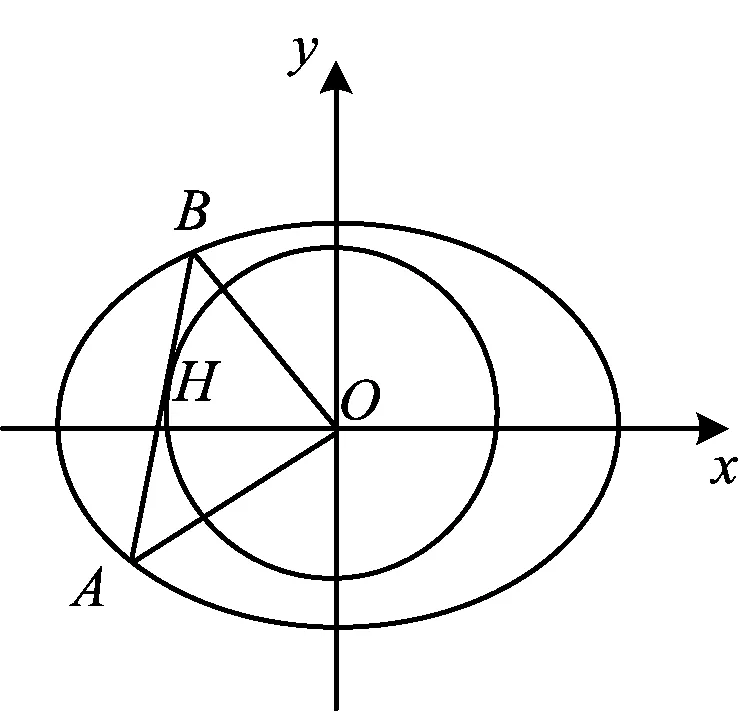
圖1

1.3 例題探究

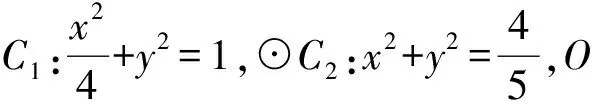
師：請同學們梳理下解題思路.

生6:設直線得參數關系→聯立橢圓方程→表示距離并消元→代入韋達定理建立目標函數,求最值.

師：思路很清晰，但計算令人崩潰，可否簡化呢？

生7:根據圖形猜測OA⊥OB，可用數量積驗證.

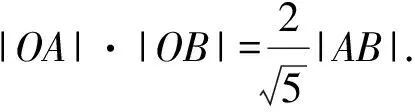
師：以上是間接用k，m表示相切和長度，可否考慮尋找|OA|,|OB|的直接關系呢？請大家以小組為單位進行探究.

設計說明數學探究是課堂教學活動的重要形式之一，是培養學生獨立思考能力的重要方式，是提升數學核心素養的重要載體，也能體現學生的主體作用.因此，設計能使學生全面參與的數學探究活動可激發學生自主學習興趣，調動學生學習的積極性.在師生互動和生生互動的過程中，教師適時地加以點撥，讓學生切實參與到知識的發生與發展中，形成適時的思維碰撞，有助于學生理解知識，同時可向學生滲透直觀想象的數學核心素養.

1.4 合作交流

設計說明解決數學問題需要一定的解題經驗為依托，這就需要學生在平時注重反思內化.教師將問題設計在學生的最近發展區，讓學生體會用數學的樂趣，感受數學知識各部分之間的聯系，同時養成良好的數學學習習慣，這不僅符合數學課程標準的要求，而且發展了運算、數據分析等數學核心素養.

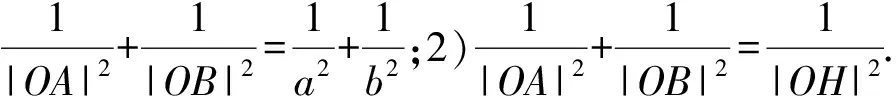
因此有線索指向可先證OA⊥OB.

證明如圖2，過點O作CD⊥OA，聯結AC,AD，并作OH1⊥AC于點H1，OH2⊥AD于點H2.因為CD⊥OA，所以

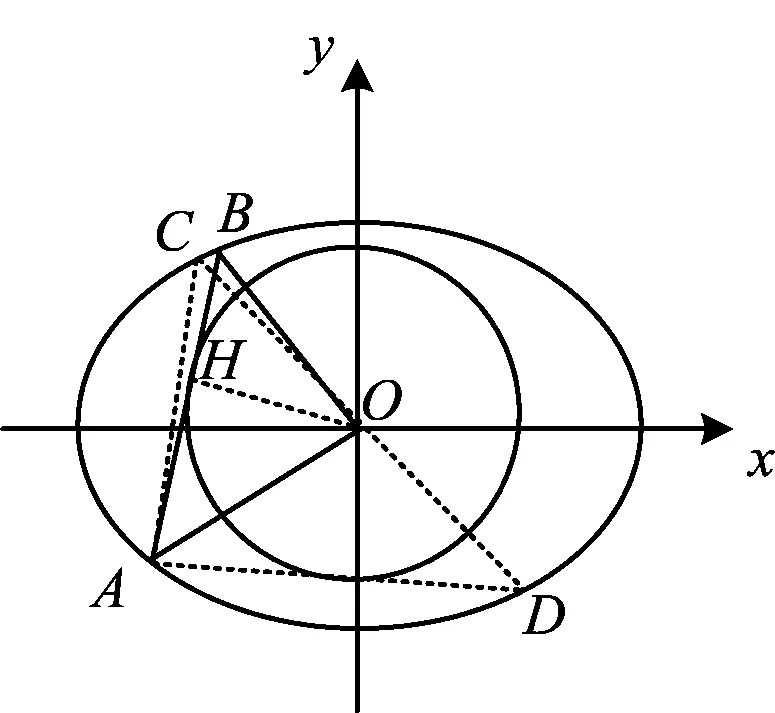
圖2

從而AC,AD為⊙O的兩條切線，點B必與點C或點D重合,因此OA⊥OB.

生9:例2轉化成了二元最值問題，可利用函數思想解決問題.

1.5 總結提煉

師：在今天的課堂上你有什么收獲呢？

(學生們闡述自己的課堂收獲.)

設計說明層層遞進式的設計將一個繁瑣的運算問題，通過幾何特征的挖掘，逐步轉化為學生所熟悉的問題模型，這不僅增強了學生解決問題的信心，培養了數學學習的興趣，還讓學生掌握了圓錐曲線問題的研究方式：代數研究幾何、幾何輔助代數.學生通過親身經歷，切身體會了優美的圖形對解題的幫助，對“欣賞圖形之美，啟發思考，引領方向”有了更深刻的認識，同時提高了學生的解題能力，進一步落實了直觀想象的數學核心素養.

2 教學反思

習題教學是數學教師必須要面對的課題，尤其是在高三的二輪復習中.如何在枯燥的習題講評中讓學生獲得一點新的感悟，讓學生在解題中有種豁然開朗的感覺，需要我們教師去精心設計課堂環節，不斷探索習題教學的高效方式，爭取讓學生在不知不覺中發展數學核心素養.

2.1 發展數學核心素養重在促進學生學會學習

俗話說：“授人以魚，不如授人以漁.”教師在教學過程中不僅要傳授學生學習經驗，加強學習指導，還應積極探索多樣化的教學方式，倡導獨立思考、動手實踐、自主探索、合作交流等學習方式.當解題遇阻時，引導學生重新回到圖形，認真審視條件，啟發思考，引領解題方向.當遇到美妙的性質與圖形關系時，點撥學生及時地體會和理解，促進學生提升對問題的認識高度，而不只是就題論題，限制想象空間，只有會當凌絕頂，才能一覽眾山小.同時應該提高作業質量，提升學生作業的時效性和自主性，及時解決和整理其中的問題，做學習的主人.這樣就能在平時不斷提升并充實自我，最終發展數學核心素養.

2.2 發展數學核心素養重在促進學生獲取思路

數學解題的推理和運算，實質都是轉化與化歸，方向都是化繁為簡、化抽象為具體、化未知為已知.思路的獲取需要在條件和結論中架起橋梁，而我們能做的只能是通過分析題目的已知與待求之間的差異，并努力消除這些差異，從中落實數學核心素養.獲取思路具體要經歷4個步驟：理解題意、提取信息、聯系舊知、重組結構.理解題意是解題的基礎，決定著解題方向，決定著能否提取到有效的信息.當學生在解題中遇到瓶頸之際，我們應該提醒學生回歸題設，包括數量關系、圖形關系以及一些隱性的關系，從中獲取啟發，進而聯系舊知，實現重構，突破難題.掌握了思考的方式，學生就能直面問題，不斷探索，進一步認識數學，發展數學核心素養.

2.3 發展數學核心素養重在促進學生反思內化

在數學學習過程中，反思是實現新舊知識相互交融、互相比較的有效途徑，是學生提升思維最有效的方法.因此，反思內化是發展數學核心素養的關鍵環節，在課堂教學中不僅要讓學生知道問題是怎么解決的，更要知道是怎么想到這個解決辦法的，以便學生在反思中對分析問題、解決問題有更深入的認識，這樣才能逐步學會用數學的眼光觀察世界、用數學的思維思考世界、用數學的語言表達世界.經常進行多層次的反思內化，是對知識框架的重新架構和再次完善，能使所學知識由“會”到“懂”再到“悟”，直到最終的“活”，才能讓學生知其然，知其所以然，更知何由以知其所以然.

2.4 發展數學核心素養重在促進學生整體把握

回歸概念和定義，厘清知識的來龍去脈，是解題的保證，也是提升解題能力的利器.離開了知識的整體結構談數學核心素養就成了無稽之談.不少學生的數學知識是碎片化的，缺少必要的整合，這就需要教師在教學中分析知識點的內在聯系，給學生示范知識的梳理，促進學生理解基本知識、掌握基本技能、體會基本思想、積累數學活動經驗，這樣才能讓數學核心素養扎根于課堂.因此，在復習教學中，教師應當幫助學生厘清各知識點在整個高中數學學習中的地位與作用，與此同時，挖掘教學內容之間的內在聯系，培養學生系統的思維習慣.

參 考 文 獻

[1] 王開林.讓數學核心素養根植于課堂——“指數函數”的教學與思考[J].中學數學教學參考，2017(11)：10-13.

[2] 范東暉.入乎其內，出乎其外——讓習題教學更有效[J].中學數學教學參考，2018(11)：47-49.

[3] 鄭花青.回歸本質：從解題教學談高考復習[J].中學數學教學參考，2017(10)：56-58.

[4] 張彬，於有海.反思：優化解題思路，簡化解題過程[J].中學數學教學參考，2018(3):57-60.