LCL型并網逆變器中PI+重復控制方法研究

(廣西大學 電氣工程學院，廣西 南寧 530004)

1 引言

隨著新能源的不斷開發與利用，人們對并網逆變技術的關注日益增加。并網逆變器作為分布式發電系統并網的接口裝置，得到了廣泛的研究。并網逆變器在并網時，采用電流控制方式，為了抑制開關頻率輸出電流諧波，傳統上采用L或LCL濾波器來抑制并網電流中的高頻諧波成分。單個L濾波器，由于其為一階系統，它在高頻段的增益與低頻段相同，因此單個L濾波器對于電流高次諧波的衰減作用較差，且需要較大的電感量，尤其是由PWM調制引起的系統開關頻率處的紋波，單個L型濾波器無法對其進行有效的衰減。LCL型濾波器作為三階系統，在高頻段增益以-40dB斜率進行衰減，能夠很好的對開關頻率處的紋波進行削減，并對電流高次諧波進行有效的抑制。同時，相對于單個L型濾波器，LCL濾波器總電感量更低，體積更小，就能達到較為良好的濾波效果，因為在逆變器系統中得到了廣泛的研究與應用[1-2]。LCL型并網逆變器控制的一個難點是其諧振問題，它的頻率響應在諧振頻率處存在諧振尖峰，同時相位會發生較大跳變，容易導致系統不穩定，因此需要對該諧振尖峰進行阻尼。有源阻尼法不改變硬件結構，通過修正控制算法來消除諧振現象，從而增強系統穩定性，如虛擬電阻法、超前網絡法等[3]。但有源阻尼法以增加控制的復雜性為代價來消除諧振，反饋量較多，對環境參數的影響更為敏感，反而降低了系統的魯棒性與可靠性。無源阻尼法通過在電容上串聯電阻來使系統穩定[4]。這種方法穩定可靠，工業中被廣泛應用。

在并網逆變器的電流控制中，常采用比例積分(proportional integral,PI)控制，盡管其結構簡單，但對于抑制低次諧波的能力有限。比例諧振(proportional resonant,PR)控制能夠抑制多個頻率的電流諧波，但需要對應數量的PR控制器，從而增加了計算量和系統的復雜程度[5]。分裂電容法和雙電感電流反饋[6]，可降低含有LCL濾波器的系統階數，但其屬于間接控制，且電網內阻抗變化等影響因素不能忽略。考慮到電網頻率的穩定性，為了進一步降低并網電流畸變率(total harmonic distortion,THD)，提高系統性能和可靠性，諸多學者提出了基于重復控制的并網逆變器電流控制策略。重復控制是近幾十年發展起來的一種新型控制方法，它通過對誤差的疊加不僅可以實現對周期性外激勵信號的高精度跟蹤控制，而且還可抑制周期性擾動，減小并網電流的THD[7]。然而單一的重復控制動態性能差，往往需要融合其他控制策略。

基于上述問題，本文采取一種將PI控制與重復控制復合的雙閉環控制策略(簡稱“PI+重復控制”)。該復合控制策略結合了PI控制器良好的動態調節性能，以及重復控制良好的穩態控制性能[8-9]。采用無源阻尼方法抑制LCL濾波器的諧振尖峰，降低控制復雜程度。最后通過仿真結果驗證了該復合控制策略能有效提高LCL型并網逆變器對諧波的抑制能力，增強系統穩定性，且具有良好的動態響應性能。

2 系統模型

單相LCL型并網逆變器電路如圖1所示。L1為逆變器側電感，C為濾波電容，L2為網側電感，它們構成LCL濾波器。推導出Uin到并網電源i2的傳遞函數為：

(1)

式中，ωr為LCL濾波器的諧振角頻率，其表達式為：

(2)

式中電感比k=L2/L1，總電感Lt=L2+L1，諧振頻率為fr=ωr/(2π)。

圖1 單相LCL型并網逆變器結構圖

根據式(1)，繪出GLCL(s)的波特圖，如圖2中的實線所示。從中可以看出，LCL濾波器的頻率響應在諧振頻率fr處存在諧振尖峰，同時相位發生-180°跳變。從控制的角度講，這個-180°跳變為一次負穿越，它會產生一對右半平面的閉環極點，導致并網逆變器不穩定。

圖2 LCL型濾波器的幅頻和相頻特性曲線

3 LCL無源阻尼補償

無源阻尼是在LCL濾波器中三個濾波器件L1、L2、C其中一個上串聯或并聯電阻，改變該器件的阻抗，能夠改變系統的阻尼系數，從而達到諧振阻尼效果，提高系統的穩定性。本文采用在濾波電容C上串聯電阻RC，如圖3所示。通過設計、選取合適的LCL濾波器參數，應對相應的阻尼電阻，從而獲得較小的阻尼損耗[10]。

圖3 濾波電容C串聯電阻

根據圖3，推導Uin到i2的傳遞函數為:

(3)

本文以1.5kVA單相逆變器為例，設計了LCL濾波器。逆變直流輸入電壓Uin=400V，開關頻率fs=10kHz，電網頻率f0=50Hz，濾波器逆變側電感為L1=1.5mH，網側電感L2=0.5mH，，濾波電容C=4.7μF。一般選取阻尼電阻為諧振頻率電容阻抗的1/3，經計算得到阻尼電阻RC=3.3Ω。結合阻尼耗損最小化參數優化設計方法[10]，當電感比k=0.33時，且RC=5Ω，無源阻尼補償達到最優化，故最終選取RC=5Ω。得到傳遞函數GLCL_1(s)的波特圖，如圖2虛線所示。

從圖2看出，在高頻段，由于電容的容抗很小，串聯電阻會增大電容支路的阻抗，從而LCL濾波器的高頻諧波衰減能力有所削弱；在低頻段，由于電容的容抗遠大于串聯電阻的阻值，串聯電阻可以忽略，因此對LCL濾波器的低頻段增益幾乎沒有影響。無源阻尼法簡單可靠，能夠很好抑制諧振尖峰，且不需要改變原系統的控制結構，減少控制難度，因此在工業界得到了廣泛的應用。

4 重復控制的模塊的頻率特性分析

重復控制是一種基于內模原理的控制策略，可有效消除控制系統內周期性的擾動和誤差，其主要應用于輸入為周期性信號的系統中。而對于逆變系統，其周期性的擾動和誤差主要在輸入信號基頻整數倍處的諧波含量。其核心結構如圖3所示，在離散域下可推導出其傳遞函數為:

(4)

式中：N=fs/f0，N為一個基波周期的采樣次數，按上節參數計算得N為200；Q是內模系數；為了使內模穩定，Q通常取值為略小于1的常數或者增益小于1的低通濾波器。當Q不同時，G(z)的波特圖如圖5所示。由圖5可知，重復控制在基波頻率和基波倍數頻率處具有高增益和零相移特性，Q越大，幅值處增益越大，系統穩態精度越高，但穩定性越差；Q越小，幅值處增益越小，控制精度較差，但穩定性較強。在實際應用中，Q取通常0.95。

圖4 重復控制器結構

根據穩定性判據和圖5所示頻率特性可知，(因為內模系數Q的存在)，G(z)本身不存在穩定性問題，LCL型被控對象通過無源阻尼補償消除了諧振尖峰以及諧振頻率處較大的相位差，所以也不存在穩定性問題。但是單一的重復控制因延遲一個周期，導致其動態性能較差。

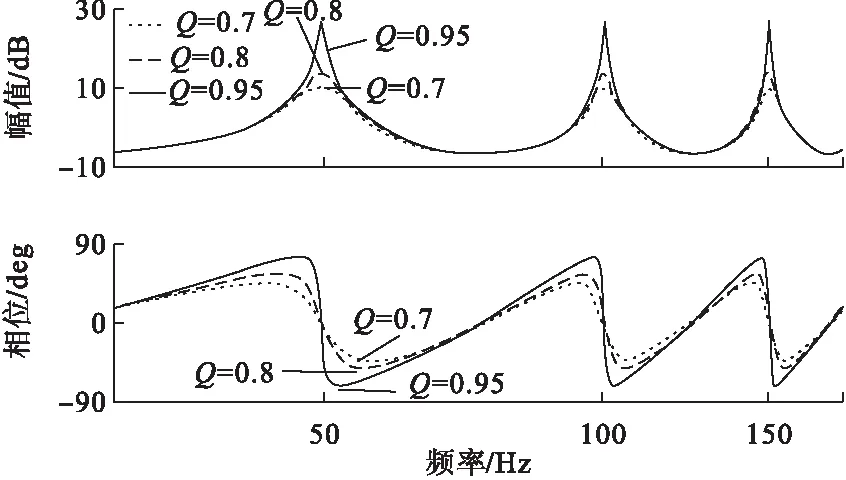
圖5 Q不同時G的波特圖

5 PI+重復控制復合控制器結構

PI控制器有良好的動態調節性能，重復控制對周期性重復的擾動信號具有較高的增益，兩者相結合組成的復合控制器既提升了LCL型并網逆變器抑制諧波能力，也改善了系統動態響應性能。由于復合控制器中引入了周期性延遲環節的重復控制有較大的控制滯后，保留PI控制的快速通路是非常必要的，其結構如圖5所示。

圖6 LCL型并網逆變的PI+重復控制結構圖

其中，補償器S(z) =KrB(z)C(z)zx，Kr為幅值補償環節，B(z)為梳狀濾波器，用于消除被控對象的諧振峰值，C(z)為二階低通濾波器，用于增加前向通道的高頻衰減能力;zx為相角補償環節，用于補償被控對象和二階低通濾波器的相移。補償器使系統在中低頻段近似保持單位增益和零相移的特性，在中高頻段增益迅速衰減，從而在整個工作頻段滿足系統的穩定性要求。

根據并網逆變器的需求，再根據實驗調整可得到并網電流PI控制器傳遞函數GPI(s)=0.15+550/s。由于選擇了無源阻尼補償和并網電流PI控制器，所以被控對象無諧振問題，故無需再設置梳妝濾波器，既B(z)=1。Kr的取值是穩定性和穩態精度折中，這里取0.9。zxc(z)將控制對象的中低頻段校正為1，而衰減高頻段以保證系統的穩定性，因重復控制中存在z-N為一個基波周期的延遲環節，使得S(z)中超前環節zx能夠實現。在高頻段，需要引入二階低通濾波器對幅度作進一步的衰減，其截止頻率一般選取為小于采樣頻率十分之一,故在此選擇截止頻率1kHz的低通濾波器。在中頻段以下，需要用超前環節zx進行補償，x值取決于被控對象和二階濾波器的合成相移大小。基于以上分析，在采樣頻率10kHz時，所設計的補償函數為:

(5)

圖7是復合控制方法下的并網系統開環傳遞函數伯德圖。可以看出，加入重復控制后，系統在輸入信號基頻50Hz的n倍頻率處有較大的幅值增益，提高了系統對諧波的抑制能力，減少系統輸出信號的穩態誤差。重復控制與PI控制復合可使得整個系統既可降低穩態誤差，又可保證系統響應的快速性。

圖7 復合控制方法下的并網系統開環傳遞函數bode圖

6 仿真結果

根據以上分析，在Simulink仿真平臺上搭建一個1.5kW單相并網逆變器模型，各參數如下，電網峰值電壓為311V，直流側電壓400V，濾波電感L1為1.5mH，L2為0.5mH，濾波電容C為4.7μF，阻尼電阻RC為5Ω，開關頻率fs=10kHz，電網頻率f0=50Hz。根據PI控制、PI+重復復合控制，這兩種控制方法得到下列輸出電壓電流波形。

圖8是在單一PI控制下單相并網逆變器的輸出電壓電流波形和輸出電壓的頻譜圖，輸出電壓和電流都正弦且穩定，其中THD為3.71%，從輸出電流頻譜可以看出，PI控制對高次諧波的抑制力度不夠。

圖9是PI+重復復合控制系統下的仿真波形，圖(a)表明復合控制系統的動態性能和PI控制一致，系統第一個周期的輸出就正弦且穩定；從圖(b)的頻譜分析中看出高次諧波的含量低， THD為1.14%，比PI控制低，印證了復合控制抑制諧波能力更優于單一PI控制。

圖8 PI控制下仿真波形

圖9 復合控制下仿真波形

7 結論

本文提出了一種單相并網逆變器并網的復合控制策略。首先分析針對LCL型并網逆變器的系統模型特點進行了分析，采用了無源阻尼法進行補償，降低控制系統復雜程度，抑制了其諧振尖峰且提高系統穩定性；其次分析重復控制內模特性，提出了PI+重復控制的復合控制策略，給出了控制器設計方法。通過仿真結果表明，該復合控制方案能有效提高LCL型并網逆變器對諧波的抑制能力，增強系統穩定性，且具有良好的動態響應性能。