非對稱支撐轉子系統的動力學行為特性研究

李 默，劉永葆，劉李歡，王 強，c

(海軍工程大學 a.動力工程學院; b.電氣工程學院; c.兵器工程學院， 武漢 430033)

軸承-轉子系統是一種典型的機械結構形式，廣泛應用在艦艇、飛機、車輛等設備中，其支撐方式以滾動軸承為支撐，滾動軸承具有復雜的非線性行為。目前，對以滾動軸承為支撐的轉子系統的研究還不夠完善，國內外一些學者應用非線性理論對滾動軸承-轉子系統進行了動力學研究，陳果、張利芹、張耀強、Tiwari、S.H.UPANDHYAY[1-5]建立了兩端都是滾動軸承為支撐的轉子系統模型，利用軸承的Hertz接觸力，綜合考慮了軸承的變剛度頻率和轉子的不平衡量，研究了軸承的徑向游隙與轉子系統的非線性行為的關系；陶海亮[6]利用有限元軟件，建立了滾動軸承-轉子系統的有限元模型，考慮了轉子不平衡量和碰摩故障的耦合作用，研究了軸承對故障耦合的影響；白長青[7]根據Floquet理論研究了軸承的徑向游隙與轉子系統周期解穩定性的關系；魏彬[8]建立了滾球軸承-轉子系統非線性動力學模型，研究了軸承的預緊力、內外滾道的曲率等結構參數對系統動力學的影響；Alireza Moazenahmadi[9]建立了有缺陷的故障滾球軸承支撐的轉子系統，研究了軸承的故障信號對系統動力學的影響；文獻[10]建立了滾柱軸承支撐的轉子系統模型，分析了軸承的缺陷故障對轉子系統的動力學影響；黃亞明、葉鵬[11-12]在研究軸承缺陷故障對滾動軸承-轉子系統的動力學影響時，建立了考慮赫茲接觸和軸承變剛度頻率的軸承-轉子模型。

以上學者建立的轉子系統模型的支撐結構都是對稱的，而且支撐軸承都是滾球軸承。但是在實際旋轉機械中，如某型艦用燃氣輪機壓氣機轉子系統，其支撐結構一端為滾球軸承，同時受到軸向力和徑向力，另一端為滾柱軸承，主要承受徑向力，起到支撐作用，該支撐結構方式的轉子系統時常發生故障。因此迫切需要開展對非對稱支撐轉子系統的非線性動力學研究，為此類旋轉機械的理論設計和故障診斷提供理論依據。

1 非對稱支撐的軸承-轉子動力學模型

圖1中，OL、OR、OP1、OP2分別為滾球軸承的形心、滾柱軸承的形心、轉子形心和轉子質心，圖2是滾動軸承的支撐模型圖，Ri是軸承的內徑，Ro是軸承的外徑。本文所構建的非對稱支撐的集中質量的轉子模型，考慮了兩類滾動軸承的非線性Hertz接觸力，并且綜合了轉盤的不平衡量，根據 Lagrange方程原理，建立了非對稱支撐的滾動軸承-轉子系統的動力學微分方程組：

(1)

方程組(1)中符號的意義見表1。

根據實際軸承轉子系統的各部分之間的連接情況，為了更好的分析軸承—轉子系統的動力學行為，做出如下假設：軸承的內滾道與轉子剛性連接；軸承的外滾道與基座剛性連接；滾動體在內、外滾道之間做純滾動運動，不產生滑移。基于以上假設，軸承的支撐力為：

當滾動軸承為滾球軸承時，n=3/2，當滾動軸承為滾柱軸承時，n=10/9。

第j個滾動單元的接觸變形量為χj=xcosθj+ysinθj-Gr。

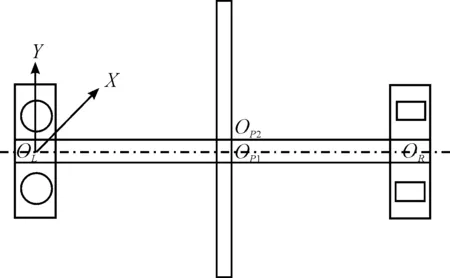
圖1 非對稱支撐的軸承—轉子系統模型圖

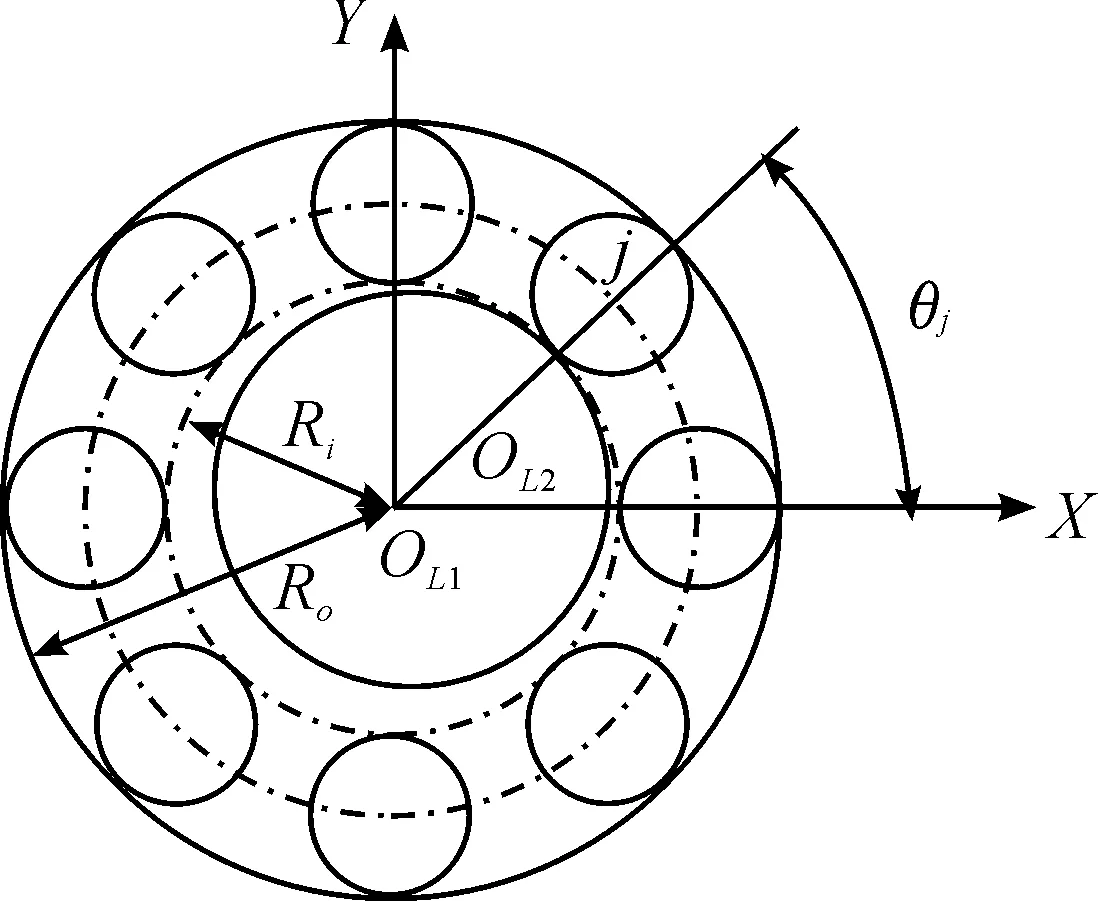
圖2 滾動軸承支撐模型圖

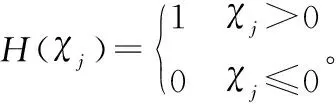
對方程(1)進行無量綱化處理，引入無量綱參數：

根據無量綱參數和方程(1)，得到如下的無量綱方程：

(2)

2 非對稱支撐軸承—轉子系統的非線性動力學數值仿真分析

2.1 模型的參數設置

本文所建立的非對稱支撐軸承—轉子系統模型中，轉盤的參數為mp=120 kg，kp=2.5×107N/m，cp=1 050 N ·s/m，e=10 μm，左端為滾珠軸承SKF 6204支撐，右端為滾柱軸承SKF NJ204ECP支撐，軸承的參數來自文獻[10]，詳細的結構參數如表2。

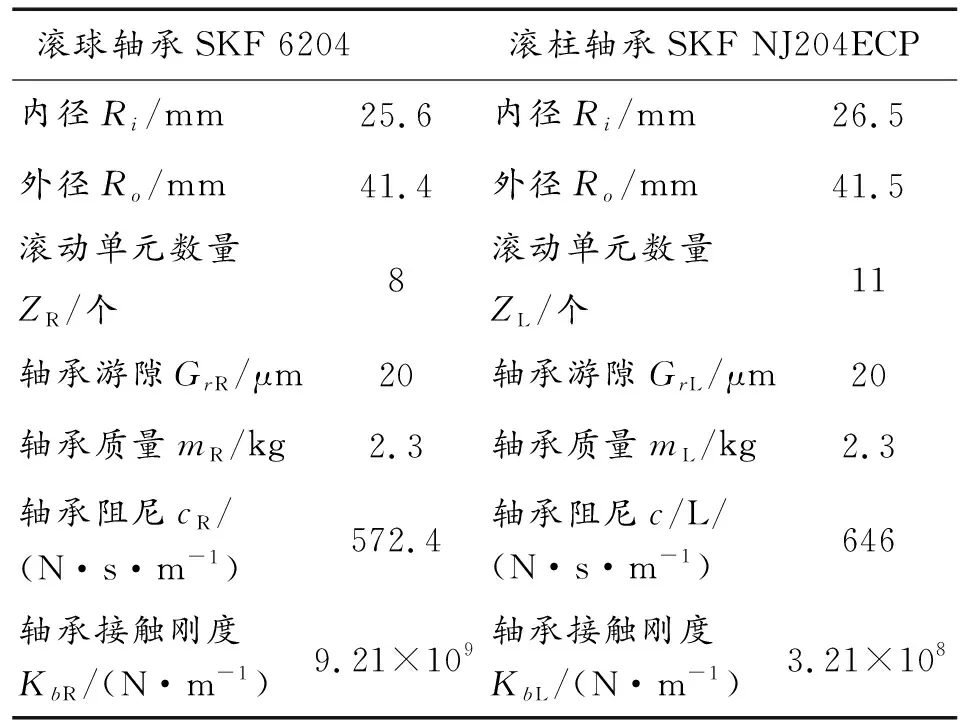
表2 軸承參數

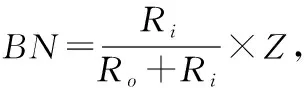
方程組(2)中的兩個軸承的支撐力是一個復雜的非線性形式的力，方程組(2)具有強烈的非線性，難以用的小參數法、平均法等近似分析方法求解析解。因此本文采用比較成熟的四階Runge-Kutta 法對非線性方程組進行數值求解，利用系統相圖、Poincare圖、FFT圖對數值結果進行可視化處理并分析，FFT圖的橫坐標為信號頻率與旋轉頻率的比值，定義為頻率比。

2.2 轉速對非對稱支撐軸承—轉子系統的動力學影響

轉速是轉子系統最基本的參數，轉子系統在啟動、正常工作和停止時，都要對轉子系統的轉速進行監測，所以必須研究轉速變化時，非對稱支撐軸承—轉子系統的非線性動力學特性。

圖3是轉盤位移xp隨轉速增加的分岔圖，從圖3可知非對稱支撐軸承—轉子系統具有較強的非線性行為。隨著系統的轉速增加，系統逐漸出現了擬周期、單周期、周期二、混沌、周期二、單周期的現象，并發現系統通往混沌的倍周期分岔途徑和陣發性途徑。

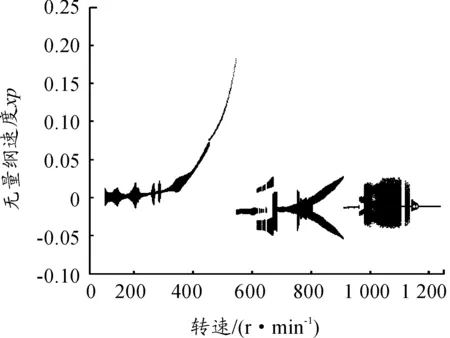
圖3 轉盤位移xp隨轉速增加的分岔圖

轉速在100～453 rad/s時，由于系統存在滾球軸承和滾柱軸承兩個變剛度頻率以及不平衡量頻率，三個頻率互相影響，存在復雜的頻率組合情況，在此轉速范圍內，出現擬周期環面破裂和重組的間隔運動。圖4(a)是轉速為100 rad/s時系統FFT圖，在頻率比為4.28處有個最大峰值，圖4(b)是轉速為150時，系統的FFT圖，在頻率比為3.05時，出現了一個最大波峰，在頻率比為4.28和1時，有兩個小的波峰，得知系統仍然為擬周期狀態，說明此時滾球軸承的變剛度頻率影響大。通過分析轉速100 rad/s和150 rad/s時的FFT圖，得知低轉速時，不平衡量頻率對轉子系統的影響比較小，支撐軸承的變剛度頻率對轉子系統影響比較大， Fukata[13]研究也表明，系統在轉速低于臨界轉速時，滾動軸承的變剛度頻率起主導作用，本文的計算結果與Fukata的結論一致，說明非對稱支撐軸承-轉子系統模型的正確性和求解結果的合理性。

轉速435～670 rad/s時，不平衡量的大小與轉速的平方成正比，隨著轉速的增加，不平衡量迅速增加，不平衡強迫振動的影響越來越大，體現為系統逐漸做以不平衡頻率為主要頻率的運動。圖5是轉速為540 rad/s時，系統轉盤出x方向的位移相圖、Poincare截面圖和FFT圖，相圖是一個封閉的圓環，Poincare截面圖集中于一點，FFT圖顯示只在不平衡量的頻率處出現峰值。

轉速在670～800 rad/s時，隨著轉速的增加，系統出現不平衡量頻率的分頻和滾動軸承兩種變剛度頻率互相影響的和或差的頻率，系統Poincare圖由不規則的封閉環形變成規則的環狀，擬周期運動逐漸穩定。圖6是轉速為670 rad/s時系統轉盤位移xp的相圖、Poincare截面圖和FFT圖，FFT圖上有三個頻率峰值，分別是不平衡量的1/3分頻諧波、不平衡量的2/3分頻諧波和不平衡量的頻率；圖7是轉速為720 rad/s時系統轉盤位移xp的相圖、Poincare截面圖和FFT圖，FFT圖上有一個頻率峰值，由此可見隨著轉速的增加，系統的分頻消失。

轉速在800～920 rad/s時，轉速增加時，系統又出現不平衡量頻率的1/2分頻諧波，擬周期環面開始破裂，出現兩個擬周期環；轉速繼續增加，1/2分頻的影響增強，兩個擬周期環越來越清晰，環面的范圍逐漸縮小，演變成周期二運動，并逐漸穩定。圖8顯示了系統的Poincare圖的變化過程。

轉速在920～978 rad/s時，系統由周期二運動倒分岔進去單周期運動，其相圖映射為一個圓環，Poincare映射圖集中于一點。圖9是轉速961 rad/s時系統的相圖、Poincare圖和FFT圖，FFT圖上只在不平衡量頻率處出現一個最高峰，隨著轉速增加，FFT圖上又出現不平衡量頻率的1/2分頻諧波，系統運動由單周期倍周期分岔進去周期二運動，這是典型的倍周期分岔行為。

轉速在978～1 139 rad/s時，如圖10和圖11，周期二變成混沌行為，FFT圖上在1/2倍分頻周圍出現連續譜，表明系統存在混沌行為。轉速增加，系統又從混沌行為進去單周期，只有不平衡量頻率，然后又進去混沌行為，這是一種通往混沌行為的陣發性途徑。

轉速在1 139～1 200 rad/s時，混沌行為演變成周期二行為，并在轉速的增加時，1/2分頻諧波的影響變小，系統逐漸穩定在單周期運動，只有不平衡量頻率出現。圖12顯示了系統的周期二運動。

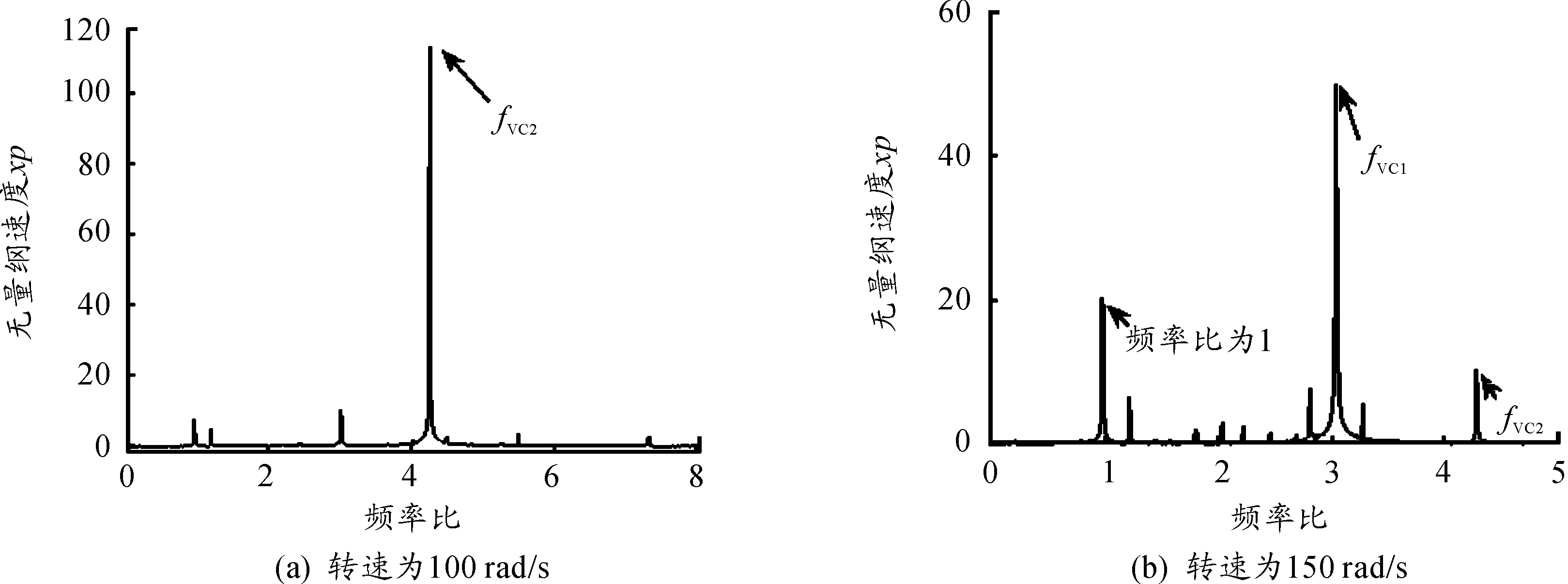
圖4 轉速為100 rad/s、150 rad/s系統的FFT圖

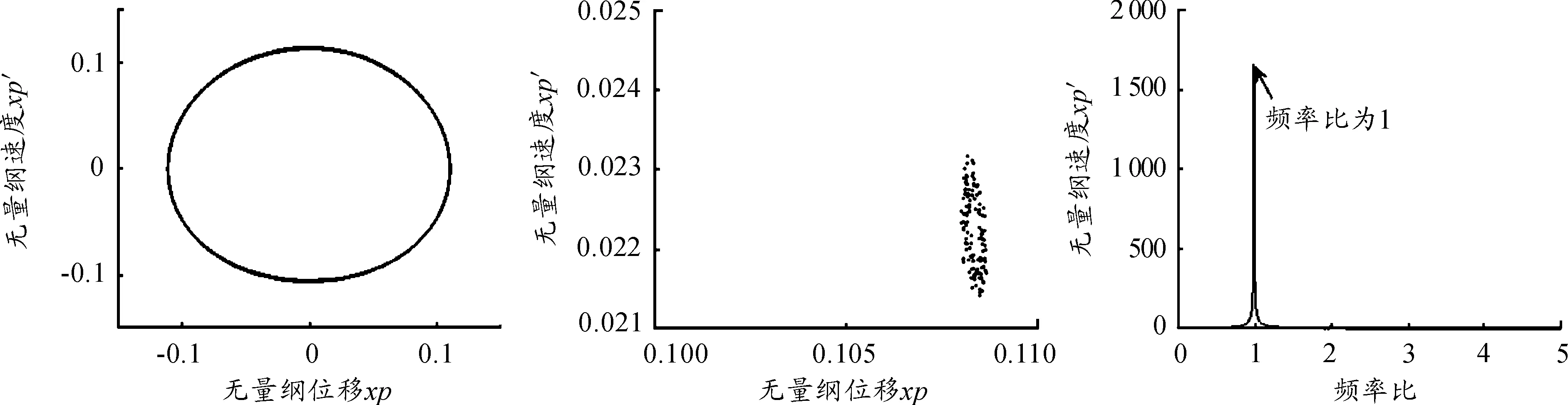
圖5 轉速為540 rad/s時系統的相圖、Poincare圖和FFT圖

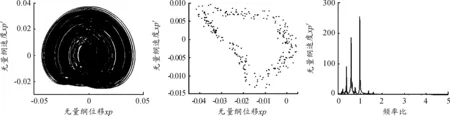
圖6 轉速為670 rad/s時系統的相圖、Poincare圖和FFT圖

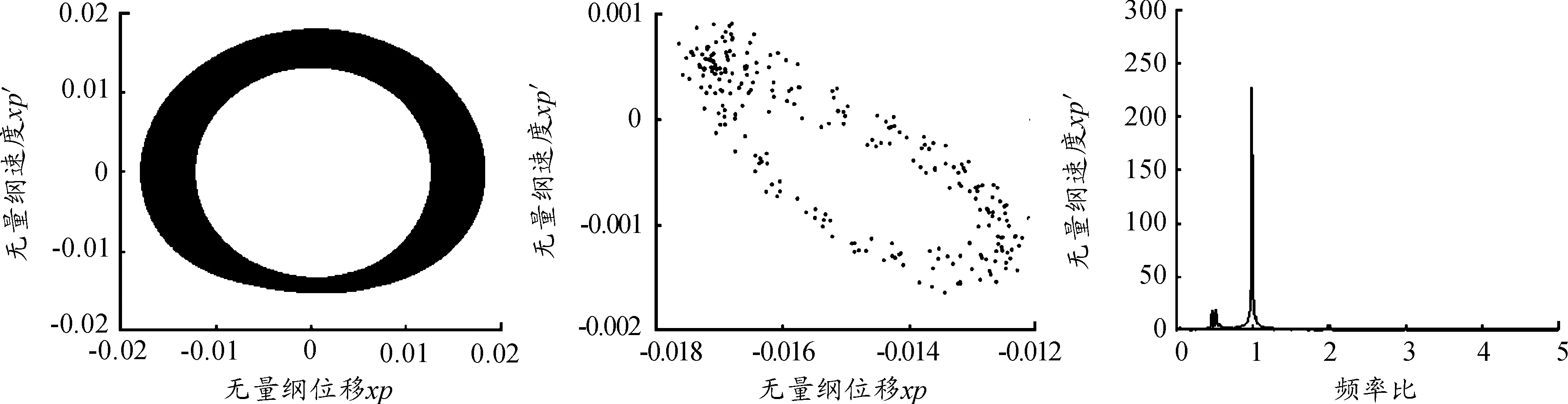
圖7 轉速為720 rad/s時系統的相圖、Poincare圖和FFT圖

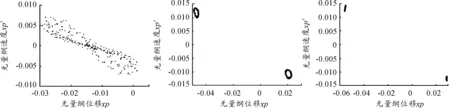
圖8 轉速為800 rad/s、890 rad/s、913 rad/s系統的Poincare圖

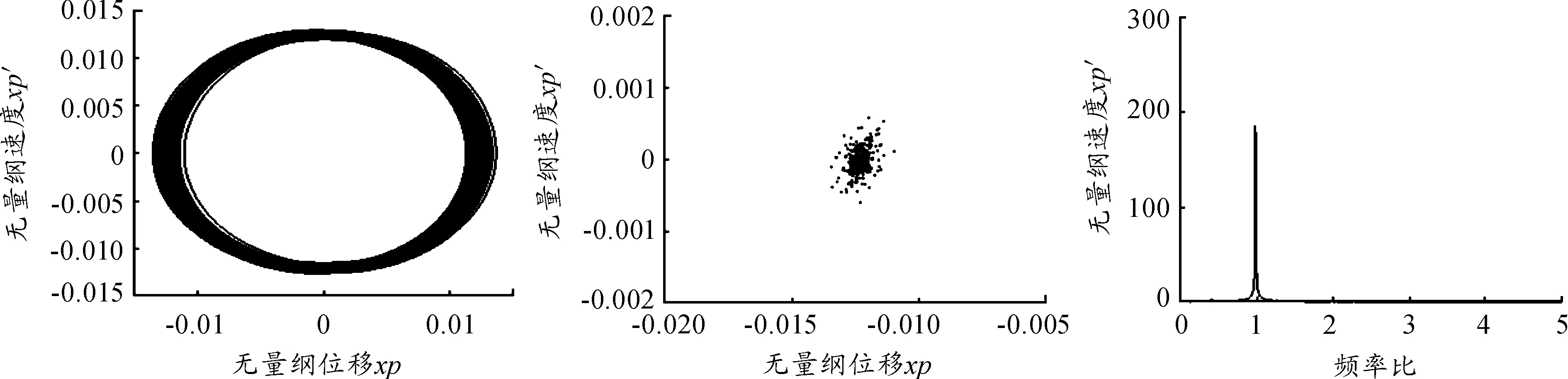
圖9 轉速為961rad/s系統的相圖、Poincare圖和FFT圖

圖10 轉速為970rad/s系統的相圖、Poincare圖和FFT圖

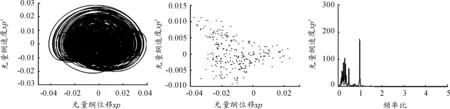
圖11 轉速為1090rad/s系統的相圖、Poincare圖和FFT圖

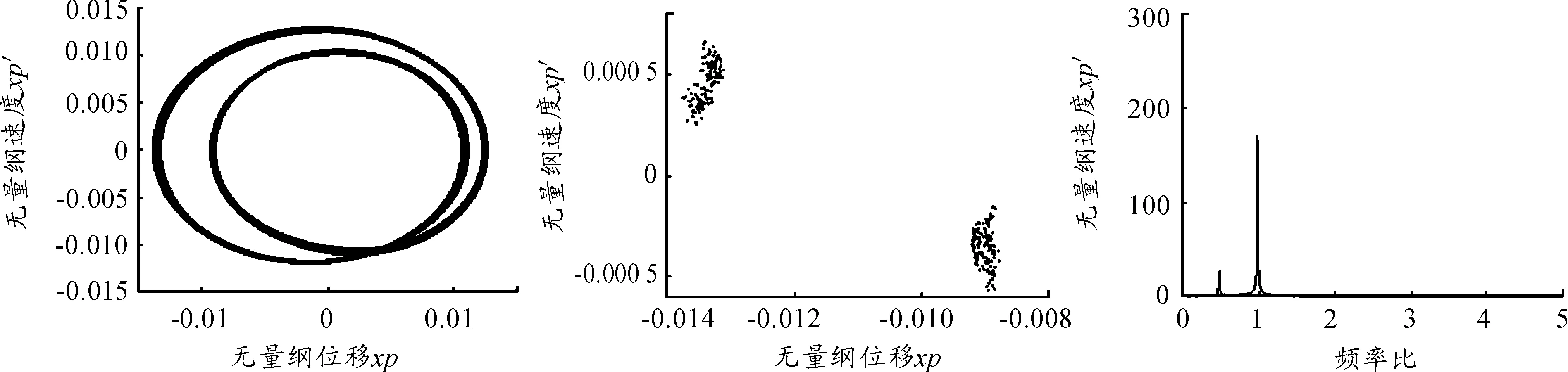
圖12 轉速為1160rad/s系統的相圖、Poincare圖和FFT圖

3 結論

1) 非對稱支撐的軸承-轉子系統存在三個頻率，滾球軸承的變剛度頻率、滾柱軸承的變剛度頻率和系統的不平衡量頻率；軸承的支撐力主要與軸承質心位移有關，不平衡量與系統轉速的平方成正比。因此低轉速時，不平衡量對系統的影響較小，系統主要表現為軸承的變剛度頻率振動與Fukata的研究結果一致，驗證了本文建立的非對稱支撐的軸承-轉子系統模型的正確性及變步長四階RK 法數值求解此類非線性方程組的合理性，并能夠滿足精度要求。

2) 在高轉速時，系統的不平衡量迅速增加，成為系統振動的主要影響因素，非對稱滾動軸承支撐的轉子系統主要出現不平衡量的1/2分頻和1倍頻。

3) 通過對轉盤處橫向位移隨轉速的分岔行為分析，發現非對稱滾動軸承支撐的轉子系統通往混沌的兩種途徑：倍周期分岔和陣發性途徑。

[1] 陳果.滾動軸承支撐下的不平衡轉子系統非線性動力響應分析[J].中國機械工程,2007,18(23):2773-2778.

[2] 張利芹.滾動軸承-轉子系統的非線性動力學分析[J].重型機械科技,2007(1):20-26.

[3] 張耀強.滾動軸承-Jeffcott 轉子系統非線性動力響應分析[J].振動與沖擊,2008,27(5):56- 59.

[4] TIWARI M,GUPTA K．Effect of radial internal clearance of a ball bearing on the dynamics of a balanced horizontal rotor[J]．Journal of sound and Vibration,2000,238(5):723- 756．

[5] UPANDHYAY S H.Analysis of Nonlinear Phenomena in High Speed Ball Bearing due to Radial Clearance and Unbalanced Rotor Effects[J].Journal of Vibration and Control,2010,16(1):65-88.

[6] 陶海亮.滾動軸承- 轉子系統非線性動力響應分析[J].燃氣輪機技術,2013,26(1):15-20.

[7] 白長青.考慮徑向內間隙的滾動軸承平衡轉子系統的非線性動力穩定性[J].應用數學和力學,2006,27(2):159-169.

[8] 魏斌.滾動軸承-轉子系統動力學特性分析[J].軸承,2012(10):1-6.

[9] ALIREZA M.A nonlinear dynamic model of the vibration response of defective rolling element bearings[J].Australian Acoustical Society,2013,17:1-7.

[10] GHAFARI S H.GOLNARAGHI F，ISMAIL F.Effect of localized faults on chaotic vibration of rolling element beariongs[J].Nonlinear Dynamic,2008,53:287-301.

[11] 黃亞明.含典型軸承故障的雙盤轉子—滾動軸承系統非線性動力學響應[C]//第十六屆全國模態分析與試驗學術會議.天津：2016.

[12] 葉鵬.滾動軸承-轉子系統缺陷故障建模及動力學行為分析[J],西安工業大學學報,2017,38(7):607-612.

[13] FUKATA.On the Radial Vibration of Ball Bearings (Computer Simulation) [J].Bulletin of the JSME,1985,28:899- 904.

[14] 葉鵬,武澎,李振.含雙時滯紊流滑動軸承-轉子系統的動力學行為分析[J].重慶理工大學學報(自然科學)，2016(8)：52-56.