SPSS軟件在導彈武器系統費用預測中的應用

尹江麗，楊曉丹

(航天工程大學 基礎部， 北京 101416)

對于武器系統費用分析,目前尚未有統一的定義[1]，美國布蘭查德教授稱之為壽命周期費用分析(life cycle cost analysis,LCCA)，他認為壽命周期費用分析是一種系統分析方法,用于選擇和確定裝備等有限資源的最佳費用,并為此而對各種方案做出必要的評價。導彈武器系統的費用分析研究是武器系統費效分析評價決策的基礎。傳統的分析方法主要采用建立完整的費用線性模型，要求樣本量大且具有較好的分布規律，預測結果與實際相差較大[2]。分析建模方法是建立在過去研制導彈武器的經驗基礎上去預測推斷待研制導彈武器系統的費用問題。在導彈武器系統的費用研究中，數理統計方法起著不可或缺的作用，尤其是統計學中的回歸分析理論是費用預測應用最多的工具之一。

回歸預測模型的計算方法很多，通常采用手工計算、Excel、Matlab等方法，但由于指標所受制約的因素往往很多，所以需要收集的數據也很多，從而導致計算過程復雜、繁瑣。SPSS (Statistical Product and Service Solutions)是當前世界上流行的統計分析軟件之一，具有強大的數據處理功能、方便易用的用戶操作方式、靈活的表格分析報告，是公認的比較優秀的統計分析軟件[3]。

由戰術導彈系統分析可知[4]，影響導彈費用的因素主要有：導彈的質量(包括導彈載體和有效載荷的質量，單位kg)、導彈的最大速度(單位Ma)及導彈的最大射程(單位海里)等，本實驗采用SPSS軟件，對影響導彈費用的一些因素進行多元線性回歸，通過一系列的檢驗方法，剔除對導彈費用影響不明顯的參數后，建立合理的多元線性回歸預測模型，以便能夠合理準確地預測待研制導彈武器系統的費用。

1 基本原理

線性回歸分析是基于最小二乘原理產生的統計分析方法，用來研究一個或多個自變量(因素)與一個因變量(指標)之間是否存在線性關系。若影響指標的因素只有一個，即只有一個自變量，就是一元線性回歸，若影響指標的因素有多個，則為多元線性回歸。多元線性回歸的數學模型為

(1)

此模型用來解決以下幾個問題：① 通過樣本估計出β0、β1、β2、…、βp的近似值，確定因變量與自變量之間的關系表達式；② 通過假設檢驗的方法對因素進行分析，影響不顯著的因素可以剔除；③通過控制自變量的數值，借助于數學模型預測或控制因變量的取值和精度[5]。

2 回歸模型及分析

收集22種各種型號導彈費用的相關數據[4](見表1)，根據這些數據，建立費用的估算模型。

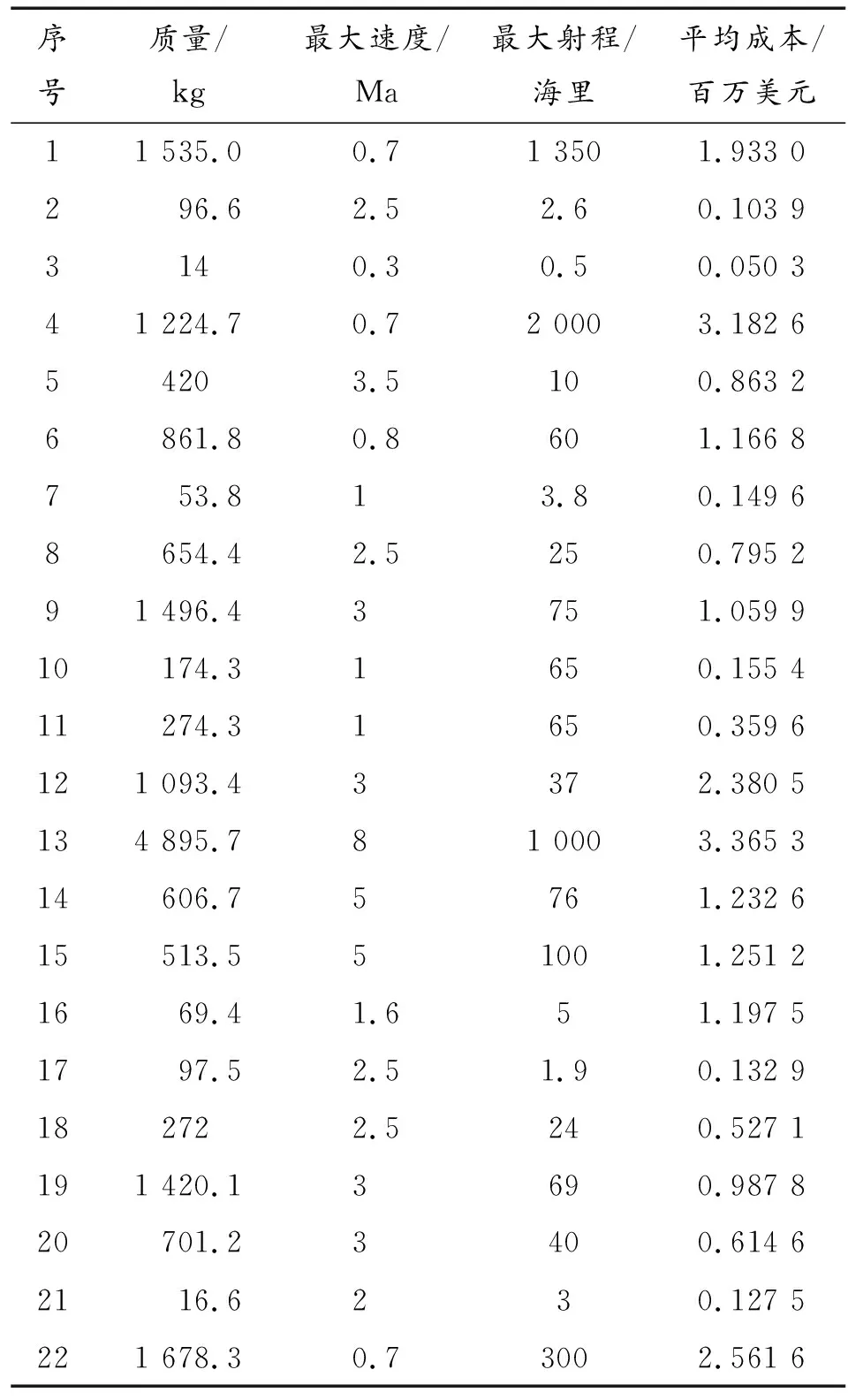
表1 22種導彈的費用數據

利用SPSS統計分析軟件，采用線性回歸模型對平均成本和導彈質量、導彈最大速度及導彈最大射程進行回歸分析，選取平均成本y為因變量，導彈質量x1、導彈最大速度x2、導彈最大射程x3作為自變量。

SPSS回歸分析過程為：首先在SPSS的數據編輯窗口輸入分析數據，然后在“分析” 菜單中進入“回歸”， 選擇“線性”，彈出線性回歸參數設置對話框。將左側列表框中“平均成本”變量添加到【因變量】列表框中，同時將“導彈質量”、“最大速度”和“最大射程”變量添加到【自變量】列表框中，在方法欄中選擇“進入”；單擊“統計量”按鈕，進入統計量對話框，分別啟用【估計】、【描述性】、【模型擬合度】和【Durbin-Watson】復選框，并單擊“繼續”按鈕，回到線性回歸對話框；其余使用默認選項，單擊“確定”按鈕運行程序[6-7]。

SPSS輸出的線性回歸分析結果如下：

1) 相關性分析

相關性分析主要顯示了各個自變量和因變量之間的關系緊密程度，數據越接近于1，表明兩者相關程度越高。從表2中可以看出，平均成本與最大速度的相關性不大。

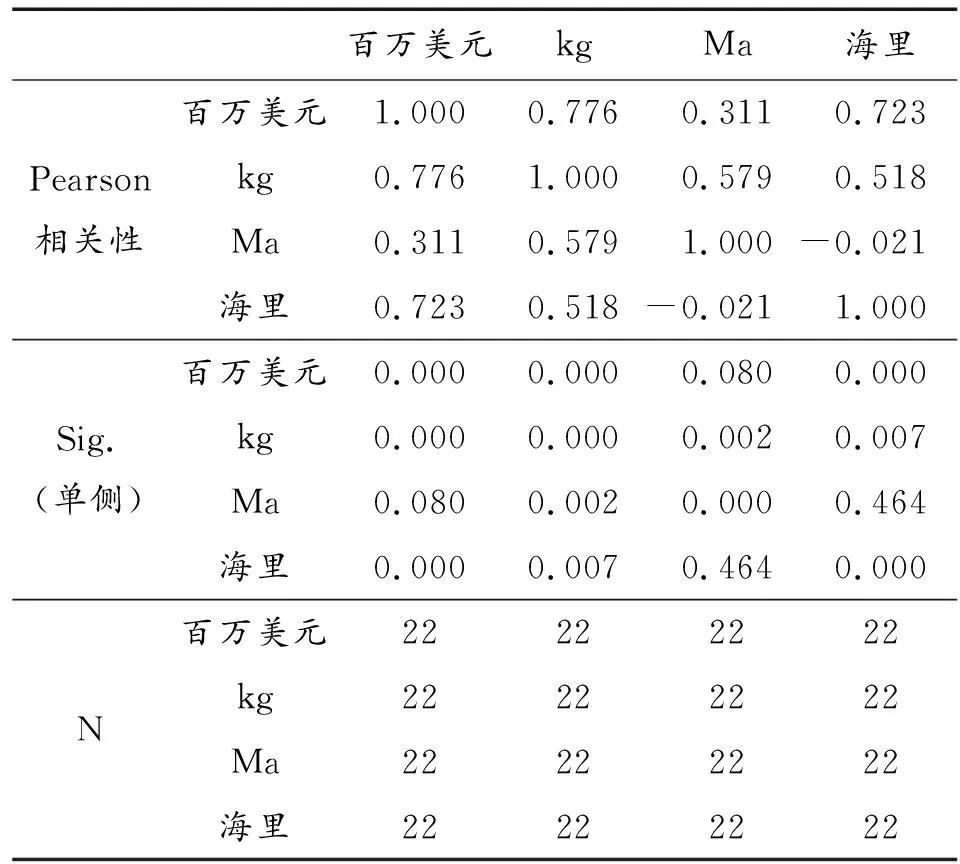
表2 變量之間的相關性分析結果

2) 擬合優度檢驗和殘差的自相關檢驗

表3 擬合優度檢驗和殘差的自相關檢驗結果

3) 回歸模型的顯著性F檢驗

此檢驗的目的是：檢驗所有自變量與因變量之間的線性關系是否顯著。從表4可以看出，F統計量的值為17.279，顯著性水平的P值幾乎為零，說明在所有自變量的共同作用下，與因變量之間的線性關系顯著。

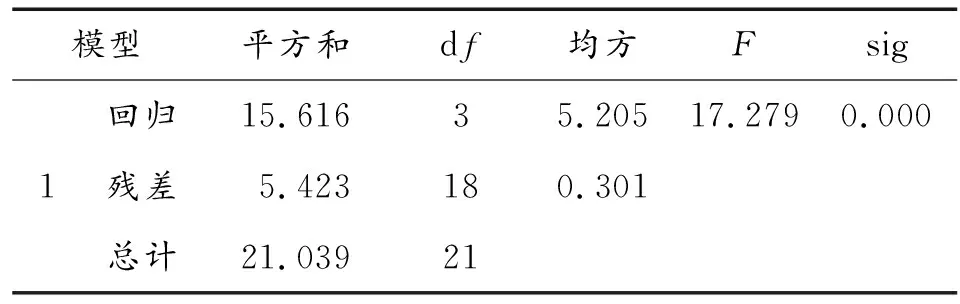
表4 回歸模型方差的F檢驗結果

4) 回歸系數的顯著性t檢驗

此檢驗的目的是：檢驗每個自變量對因變量的影響，不顯著的予以剔除。從表5可以看出，此回歸模型中最大速度的t值較小，檢驗的p值為0.978,大于顯著性水平0.05，故此變量對平均成本的影響不太顯著，應該剔除。由此可以看出，模型雖然通過了顯著性F檢驗，但很有可能不能通過變量的顯著性檢驗。

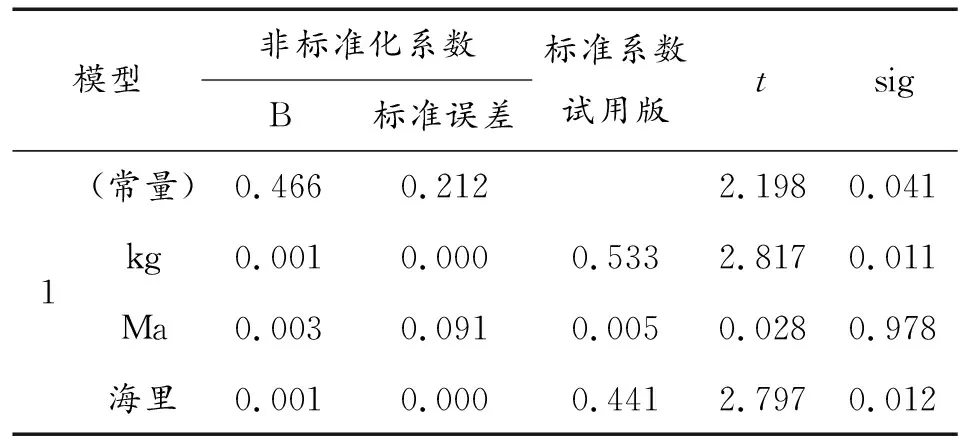
表5 回歸系數的顯著性t檢驗結果

5) 殘差分析

表6顯示了預測值、殘差、標準化預測值、標準化殘差的相關數據，根據概率的3σ準則，標準化殘差的絕對值最大為2.397，小于3，說明樣本數據中沒有異常值。

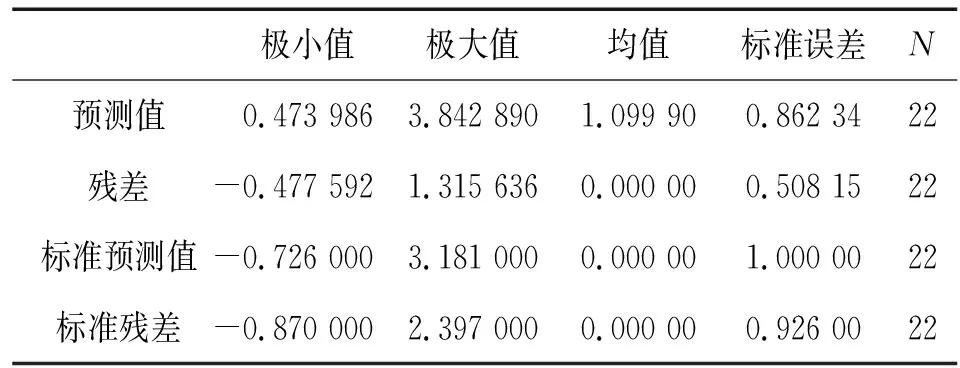
表6 殘差分析結果

6) 最終預測模型

模型剔除導彈最大速度x2后，用本次實驗中使用的方法和步驟重新對平均成本y，導彈質量x1、導彈最大射程x3作進行線性回歸分析。得到的主要結果如表7～表10所示。

表7 剔除x2后擬合優度檢驗和殘差的自相關檢驗結果

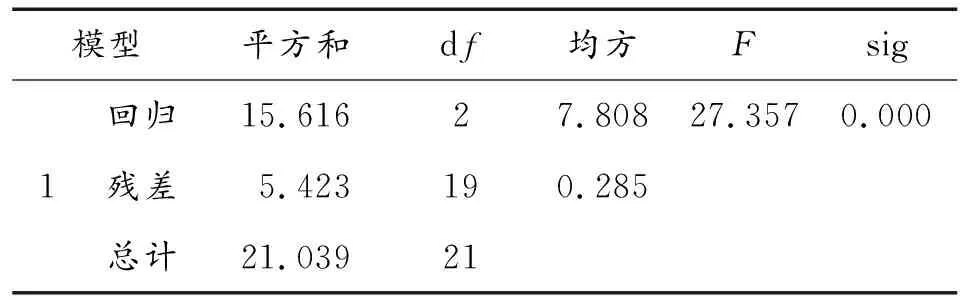
表8 剔除x2后方差的F檢驗結果

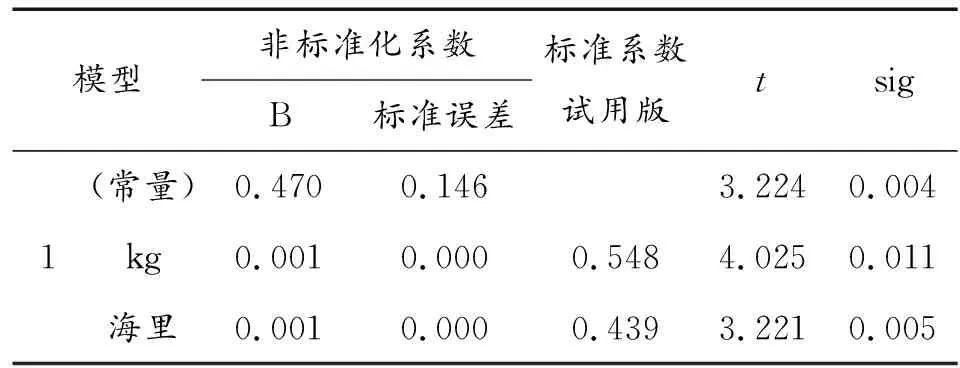
表9 剔除x2后回歸系數的顯著性t檢驗結果

表10 剔除x2后殘差分析結果

從表7～表10可以看出：剔除變量x2后，模型的擬合優度和DW值變化不大，擬合效果很好且變量無序列相關性；方差的F檢驗與原來模型結論相同，自變量與因變量之間線性關系顯著；與原來的模型相比，變量x1和x3均通過了顯著性t檢驗，因此模型更加合理，故最終的預測模型為

y=0.470+0.001x1+0.001x3

(2)

假如已知某型號導彈質量為984.5 kg，最大射程為80海里，則可以預測其成本約為

y=0.470+0.001×984.5+0.001×80=1.534 5(百萬美元)

3 結論

利用SPSS軟件對導彈成本進行回歸分析，建立回歸模型，通過對模型的一系列檢驗，剔除較弱關系的自變量，對模型進行修正后最終給出了導彈平均成本的預測模型，SPSS回歸分析是導彈費用指標測定的一種有效方法。

[1] 于向軍，王偉海.武器系統費用分析的發展現狀及對策建議[J].軍事經濟研究，2012(1)：50-52.

[2] 楊志剛，王海濤.艦空導彈武器裝備壽命周期費用分析[J].兵工自動化，2013(10)：4-7.

[3] 楊光霞.SPSS數據統計與分析[M].北京:清華大學出版社,2014:203-208.

[4] 文仲輝.戰術導彈系統分析[M].北京:國防工業出版社,2000:274-275.

[5] 滕素珍.數理統計學[M].大連:大連理工出版社,2005:172-244.

[6] 馮國生.SPSS統計分析與應用[M].北京:機械工業出版社,2014:84-96.

[7] 湯澤姣，朱克喜.基于SPSS回歸分析對中長期居民用電負荷預測 [J].貴州電力技術,2010,13(7):24-27.