基于JADE的和差四通道抗多主瓣干擾算法

， ， ，

(空軍預警學院重點實驗室， 湖北武漢 430019)

0 引言

隨著信息化戰的不斷推進，戰場電磁環境日趨復雜、瞬息萬變。近年來美軍裝備的EA-18G“咆哮者”電子戰機以及各式各樣的彈載干擾機所釋放的主瓣干擾已經對我方雷達構成現實威脅。當前，副瓣干擾抑制技術已較為成熟，比如副瓣對消、副瓣匿影、頻率捷變、低副瓣/超低副瓣等，但對抗主瓣干擾卻無能為力，對抗多主瓣干擾更是一個難題。主瓣干擾可以分為兩類：第一類是自衛式干擾，由目標機所攜帶的干擾機施放，已有較為成熟的對抗措施[1-2]。第二類是近主瓣干擾，這類干擾從波束主瓣進入，但和目標機有一個角度差，比如和目標機編隊飛行的隨隊干擾機、彈道導彈施放的彈載干擾機等。目前尚無有效措施應對此類干擾。本文針對抗近主瓣干擾技術展開研究，為方便閱讀，文中均以“主瓣干擾”代替“近主瓣干擾”的說法。

在空域抗主瓣干擾方面，自適應數字波束形成技術[3-6](Adaptive Digital Beamforming, ADBF)在主瓣干擾抑制過程中存在主瓣指向偏移、旁瓣升高等問題，導致目標信號損失嚴重；Applebaum等給出了和差主瓣干擾相消器[7](Mainlobe Canceller, MLC)，但無法同時抑制副瓣干擾；Yu等將ADBF和MLC進行級聯，實現對副瓣干擾和主瓣干擾分步抑制[8-9]；周必雷等將前者推廣到子陣級應用中[10]；饒燦等提出了多點約束下的自適應抗主瓣干擾方法[11]，可有效解決主瓣干擾環境下單脈沖曲線畸變而導致無法測角的問題；李榮鋒等提出了和差及輔助波束聯合自適應單脈沖方法[12]，可在同時抑制主副瓣干擾的同時較好地得到目標的空間位置信息。但是這些方法[7-12]均只能夠抑制1個主瓣干擾。在極化域上進行抗主瓣干擾方面[13-16]，存在的突出問題是要求每個通道均為正交雙極化通道，因此成本較高、工程不易實現。在時域抗主瓣干擾方面，對于從主瓣進入的強壓制干擾，可以尋找干擾與信號的顯著特征差異。其中，解析重構[17]主瓣壓制干擾的抑制效果較好，但前提是要求干擾能量很強且幅度變化不太劇烈。在聯合域方面，丁黎明等提出了基于稀疏恢復的抗主瓣干擾方法[18-20]，在空時平面上較好地恢復得到原始信號，但是該類方法對噪聲較為敏感。另外，在頻域方面的頻率捷變方法、功率域方面的波位燒穿方法等對抗主瓣干擾并無有效得益。

可見，在空、時、頻、功率、極化域以及聯合域上在對抗主瓣干擾方面都存在著一些難以克服的問題，尤其是面對多主瓣干擾更是難以奏效。因此，可以換一種思路，不從干擾抑制的角度出發，而是考慮對目標和干擾進行分離，只要得到目標，即實現了干擾抑制的目的。本文利用盲源分離技術對環境中存在的信源進行分離，繼而進行脈壓以提取目標回波信號。術語“盲”有兩重含義[21]：1)源信號不能被觀測；2)源信號如何混合是未知的。顯然，當從源信號到傳感器之間的傳輸很難建立起數學模型，或者關于傳輸的先驗知識無法獲得時，盲信號分離是一種很自然的選擇。

目前，國內部分研究者已經開始了基于盲源分離技術的抗主瓣干擾方法研究工作[22-25]。王文濤等[22]利用基于尋找峭度的局部極值點的Fast ICA 盲分離算法分離接收到的主瓣干擾混合信號，再通過脈壓尋找目標信號，實現主瓣干擾的有效抑制；王建明等[23]提出了基于矩陣聯合對角化(JADE)的盲源分離算法，采用雙波束(分別指向目標和干擾方向)抗干擾；文獻[24]首先利用蓋氏圓半徑法對信源數預估計，以保證抗干擾算法的有效性，再應用JADE盲分離算法進行信源分離達到抑制主瓣干擾的目的；文獻[25]提出的FRFT后置降噪的盲分離抗主瓣干擾算法，相比JADE法在干擾抑制比上有一定程度的提高。然而，以上提到的這些算法也只能抑制1個主瓣干擾，對于多主瓣干擾無能為力。

本文利用平面相控陣形成和差四通道接收混合信源，再用盲分離技術進行信源分離，最后通過脈壓處理提取目標回波信號，達到抑制多主瓣壓制干擾的目的。

1 信號模型

考慮N1行N2列矩形面陣，模型如圖1所示。在x和y方向的陣元間距均為d。θ，φ分別表示入射信號的方位角、俯仰角，信號波長為λ。假設環境中存在1個目標和M個主瓣干擾，分別位于(θm,φm)(m=0,1,…,M,M≤3)，陣列通道噪聲為相互獨立的零均值高斯白噪聲，主波束指向目標方向。

以主瓣干擾數M=3為例，空間中存在1個目標S0和3個主瓣壓制干擾ji(i=1,2,3)，則四通道接收到的信號為：

1)和通道接收和波束的信號

rΣ(t)=a0s0(t)+a1j1(t)+a2j2(t)+

a3j3(t)+nΣ(t)

(1)

式中，nΣ(t)為和通道的噪聲，ai(i=0,1,2,3)分別為和通道對s0(t),ji(i=1,2,3)的響應。

2)方位差通道接收方位差波束的信號

rΔA(t)=b0s0(t)+b1j1(t)+b2j2(t)+

b3j3(t)+nΔA(t)

(2)

式中，nΔA(t)為方位差通道的噪聲，bi(i=0,1,2,3)分別為方位差通道對s0(t),ji(i=1,2,3)的響應。

3)俯仰差通道接收俯仰差波束的信號

rΔE(t)=c0s0(t)+c1j1(t)+c2j2(t)+

c3j3(t)+nΔE(t)

(3)

式中，nΔE(t)為俯仰差通道的噪聲，ci(i=0,1,2,3)分別為俯仰差通道對s0(t),ji(i=1,2,3)的響應。

4)雙差通道接收雙差波束的信號

rΔΔ(t)=d0s0(t)+d1j1(t)+d2j2(t)+

d3j3(t)+nΔΔ(t)

(4)

式中，nΔΔ(t)為雙差通道的噪聲，di(i=0,1,2,3)分別為雙差通道對s0(t),ji(i=1,2,3)的響應。

將這4個通道接收到的混合信號進行數字化，并合成矩陣形式可以表示為

(5)

式(5)可寫為

r(n)=HS(n)+N(n)

(6)

式中，

混合矩陣H可以表示為

(7)

式中，a(θi,φi)(i=0,1,2,3)分別表示s0(t),j1(t),j2(t),j3(t)的導向矢量，a(θi,φi)=a(φi)?a(θi)，?為Kronecker積，a(φi)=[1,e-jαi, …,e-j(N1-1)αi]，a(θi)=[1,e-jβi,…,e-j(N2-1)βi] ，αi=2πdsinφi/λ，βi=2πdcosθicosφi/λ。wΣ，wΔE，wΔA，wΔΔ分別表示和波束、俯仰差波束、方位差波束及雙差波束的加權矢量：

(8)

式中，wTaylor_x，wBay_x分別表示x方向上的N2維Taylor權和貝里斯權，wTaylor_y，wBay_y分別表示y方向上的N1維Taylor權和貝里斯權。

2 算法原理

基于盲分離的抗多主瓣干擾算法需要滿足以下3個條件：

1)信源數M+1≤雷達通道數N。本文采用的是和差四通道，因此，包含目標回波后，環境中至多存在3個主瓣干擾。

2)各信源之間相互獨立且至多含有一個高斯信號，實際環境滿足此條件。

3)混合矩陣H列滿秩。本文采用的和差四波束作為空域通道，可使得混合矩陣滿足列滿秩。

本文目的在于抗多主瓣干擾并保證目標的距離信息不受損失，將混合信號r(t)中的目標回波信號s0(t)分離出來，然后進行脈壓提取目標回波信號，以達到抗干擾的目的。以主瓣干擾數M=3為例，具體算法步驟如下：

1)信源混合過程：r(n)=HS(n)+N(n)。

2)白化過程：Z(n)=Wr(n)，W為白化矩陣，可以通過接收信號r(n)的協方差矩陣Rrr的子空間估計得到：

(9)

w=(PD-1/2)H

(10)

式中，D為Rrr的大特征值矢量，P為特征向量矩陣，由每個特征值所對應的特征向量組合而成。

白化信號Z(n)還可表示為

Z(n)=Wr(n)=WHS(n)+WN(n)=

US(n)+WN(n)

(11)

可見，若要恢復源信號S(n)，必須估計酉矩陣U。

3)求白化信號的四階累積量矩陣QZ(M)：取任意4×4矩陣M，求白化后的四通道觀測矢量Z(n)的四階累積量矩陣QZ(M)，其定義如下：它的第ij個元素[QZ(M)]ij為

i,j=1,2,3,4

(12)

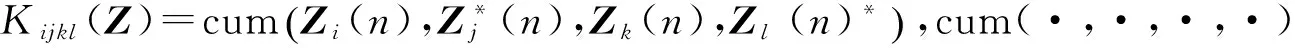
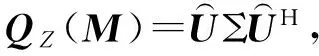
(13)

(14)

conv(·，·)是卷積運算，采用峰值檢測即可提取目標回波信號，從而抑制干擾。

3 仿真實驗及性能分析

陣列采用22×48的均勻面陣，發射信號采用線性調頻信號，帶寬B=5 MHz,脈寬τ=100 μs，采樣率fs=5 MHz，陣元間距為半波長。俯仰和、方位和的波束靜態加權均為-35 dB的Chebyshev權，俯仰差、方位差的波束靜態加權均為-35 dB的Bayliss權，波束指向(90°, 30°)。方位向、俯仰向和波束的半功率波束寬度分別為3.2°,7.1°。目標位于第3 000個距離單元，方位角90°，俯仰角30°。陣元級信噪比為-28.5 dB(波束合成及脈壓后為20 dB)。

仿真1：干擾位于主波束的1/4波束寬度(方位向及俯仰向)時的分離效果

仿真條件：分別在以下4種干擾環境下的盲分離后目標檢測情況。①1個MLJ，主瓣干擾位于(90.8°, 31.775°)；②1個MLJ+1個SLJ，主瓣干擾位于(90.8°, 31.775°)，副瓣干擾位于(40°, 30°)；③2個MLJ，2主瓣干擾分別位于(90.8°, 31.775°)，(89.2°，31.775°)；④3個MLJ，3個主瓣干擾分別位于(90.8°, 31.775°)，(89.2°，31.775°)，(89.2°，28.225°)。所有的干噪比(INR)均為50 dB。

圖3給出了1個主瓣干擾環境下的和差四通道混合信號的脈壓波形，可見目標回波均淹沒在干擾中。圖4給出了在4種干擾環境下經過盲分離后的脈壓波形，波形尖峰清晰可見，可檢測到目標信號。由圖3(a)及圖4(a)分析可見，主瓣干擾抑制比將近50 dB，即基本完全抑制了主瓣干擾，回波信噪比約為18 dB，與原定設置的20 dB只相差了2 dB，達到了較好的目標信息提取效果。

當干噪比較低時，以環境中存在3個主瓣干擾為例，取INR=25 dB及INR=5 dB，由圖5可見，目標回波信噪比改善依然為18 dB左右，可見，分離效果并不受主瓣干擾強度大小的影響。

仿真2：干擾分別位于主波束的1/6,1/8,1/10波束寬度時的分離效果

仿真條件：設置3個MLJ，INR均為50 dB，干擾位置如表1所示。

表1 3個MLJ角度設置

由圖6可見，即使將干擾位置離目標更近時，即在1/6，1/8，1/10半功率波束寬度上，經過盲分離處理后仍然能夠得到目標信號。因此，相比較于空域自適應主瓣對消方法[7,10,12]基本上只能有效抑制位于1/4個波束寬度以外的干擾并保留目標信號，新方法可以在更為惡劣的主瓣干擾環境下保證良好的目標檢測性能。

4 結束語

當干擾落入雷達波束主瓣內時，通常能量都很強，可以將目標回波信號完全淹沒，嚴重影響雷達的目標檢測性能。面對主瓣干擾，常用的副瓣相消、匿影、低副瓣等針對副瓣干擾的方法是無效的。另外，目前已有的針對主瓣干擾的抑制方法研究也只能夠應對一個主瓣干擾，滿足不了實際戰場電磁環境的要求，尤其是面對美軍的EA-18G電子干擾機以及彈載干擾機等。因此，本文提出了一種基于JADE的和差四通道抗多主瓣壓制干擾算法，可有效抑制多個主瓣干擾，在工程實現上也較為簡單，可以應用于現有的相控陣雷達體制。另一方面，相對于空域的主瓣干擾相消方法只能夠有效應對位于1/4波束寬度以外的主瓣干擾而言，新方法可在更為惡劣的主瓣干擾環境下(主瓣干擾位于1/10波束寬度)依然有效保留目標信號。

參考文獻：

[1] 李永禎, 王國玉, 汪連棟, 等. 基于雷達輔陣的自衛壓制式干擾極化對消方法研究[J]. 信號處理, 2008, 24(5):775-779.

[2] 李迎春, 王國宏, 孫殿星, 等. 雷達抗自衛轉發式航跡假目標欺騙干擾技術[J]. 系統工程與電子技術, 2015, 37(6):1242-1248.

[3] 陳希信, 韓彥明, 于景蘭. 高頻雷達自適應波束形成抗干擾研究[J]. 電波科學學報, 2010, 25(6):1169-1174.

[4] APPLEBAUM S. Adaptive Arrays[J]. IEEE Trans on Antennas and Propagation, 1976, 24(5):585-598.

[5] JABLON N. Adaptive Beamforming with the Generalized Sidelobe Canceller in the Presence of Array Imperfections[J]. IEEE Trans on Antennas and Propagation, 1986, 34(8):996-1012.

[6] SHAN T J, KAILATH T. Adaptive Beamforming for Coherent Signals and Interference[J]. IEEE Trans on Acoustics, Speech, and Signal Processing, 1985, 33(3):527-534.

[7] APPLEBAUM S P, WASIEWICZ R. Main Beam Jammer Cancellation for Monopulse Sensors[R]. Fort Belvoir, VA: Defense Technical Information Center, 1984.

[8] YU K B, MURROW D J. Adaptive Digital Beamforming for Angle Estimation in Jamming[J]. IEEE Trans on Aerospace and Electronic Systems, 2001, 37(2):508-522.

[9] YU K B, MURROW D J. Combining Sidelobe Canceller and Mainlobe Canceller for Adaptive Monopulse Radar Processing: US6867726[P]. 2005-03-15.

[10] 周必雷, 李榮鋒, 戴凌燕, 等. 子陣級和差及輔助波束聯合自適應單脈沖測角算法[J]. 雷達科學與技術, 2014, 12(4):379-388.

ZHOU Bilei, LI Rongfeng, DAI Linyan, et al. Adaptive Monopulse Algorithm Based on Combining Sum-Difference and Auxiliary Beam for Anti-Jamming at Subarray Level[J]. Radar Science and Technology, 2014, 12(4):379-388. (in Chinese)

[11] RAO Can, LI Rongfeng, DAI Lingyan. Monopulse Estimation with Multipoint Constrained Adaptation in Mainlobe Jamming[C]∥ IEEE CIE International Conference on Radar, Chengdu: IEEE, 2011:1054-1057.

[12] LI Rongfeng, RAO Can, DAI Lingyan, et al. Combining Sum-Difference and Auxiliary Beam for Adaptive Monopulse in Jamming[J]. Journal of Systems Engineering and Electronics, 2013, 24(3):372-381.

[13] 宋立眾, 喬曉林, 吳 群. 一種基于極化DBF的制導雷達抗干擾方法[J]. 電波科學學報, 2010, 25(1):109-115.

[14] 戴幻堯, 李永禎, 劉勇, 等. 主瓣干擾極化抑制的新方法[J]. 中國科學: 信息科學, 2012, 42(4):460-468.

[15] DAI Huanyao, WANG Xuesong, LI Yongzhen, et al. Main-Lobe Jamming Suppression Method of Using Spatial Polarization Characteristics of Antennas[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(3):2167-2179.

[16] 王峰, 雷志勇, 李婧. 一種自適應正交虛擬極化抗主瓣干擾方法研究[J]. 中國電子科學研究院學報, 2013, 8(1):53-55.

[17] 杜東平. 雷達壓制式干擾抑制算法研究[D]. 成都: 電子科技大學, 2008.

[18] DING Liming, LI Rongfeng, WANG Yongliang, et al. Discrimination and Identification Between Mainlobe Repeater Jamming and Target Echo by Basis Pursuit[J]. IET Radar, Sonar and Navigation, 2017, 11(1):11-20.

[19] DING Liming, LI Rongfeng, DAI Lingyan, et al. Discrimination and Identification Between Mainlobe Repeater Jamming and Target Echo via Sparse Recovery[J]. IET Radar, Sonar and Navigation, 2017, 11(2):235-242.

[20] DING Liming, DAI Lingyan, LI Rongfeng, et al. Discrimination and Identification of Time-Delay Repeater Jamming and Target Echo by Basis Pursuit[J]. IET International Radar Conference, Hangzhou: IET, 2015:1-4.

[21] 張賢達, 保錚. 盲信號分離[J]. 電子學報, 2001, 29(12A):1766-1771.

[22] 王文濤, 周青松, 劉興華, 等. Fast ICA盲分離算法在雷達抗主瓣干擾中的應用研究[J]. 現代雷達, 2015, 37(12):40-44.

[23] 王建明, 伍光新, 周偉光. 盲分離在雷達抗主瓣干擾中的應用研究[J]. 現代雷達, 2010, 32(10):46-49.

[24] 王文濤, 張劍云, 劉興華, 等. JADE盲源分離算法應用于雷達抗主瓣干擾技術[J]. 火力指揮與控制, 2015, 40(9):104-108.

[25] 周青松, 王文濤, 王珽, 等. 盲分離算法和FRFT聯合抗雷達主瓣干擾技術研究[J]. 信號處理, 2015, 31(8):1004-1011.