整個非干涉光場的相位檢索算法研究

吳海燕

(安徽三聯(lián)學院，安徽 合肥 230601)

3D光場重構(gòu)技術(shù)需要預先獲取場景的深度信息，但是光場的振蕩頻率極高，常規(guī)光學傳感器只能記錄光場強度，丟失了包含物體形狀細節(jié)和深度等的相位信息。相位檢索技術(shù)是指利用直接測量得到的強度信息通過計算的方法得到相位，為全光場重構(gòu)進而實現(xiàn)3D顯示提供所需要的數(shù)據(jù)信息。經(jīng)典的非干涉相位恢復技術(shù)通過求解強度傳輸方程(Intensity Transport Equation，TIE)從強度中恢復相位，在相干光場中獲得了廣泛應用。還有一種經(jīng)典算法是迭代算法。其中，迭代相位恢復使用物面和像面的強度數(shù)據(jù)來恢復輸入和輸出平面上的光場相位分布[1]，多數(shù)時候能夠很快地收斂并得到誤差較小的結(jié)果，但在實際計算中，情況并不是很理想。強度傳輸方程是Teague[2]于1983 年由亥姆霍茲方程在傍軸近似下首次推導得到的。該方法不是通過傳統(tǒng)的衍射計算公式來迭代恢復相位，而是在光強軸向微分以及光強分布已知的情況下，通過數(shù)值求解光強傳輸方程直接地獲取相位信息，從而不需要任何的迭代求解過程，但是只適合近場。所以這些經(jīng)典的算法各自存在優(yōu)缺點，還有很大的改進空間。

基于兩種算法的適用情況，從整個衍射光場出發(fā)，本文提出了不同距離的衍射光場的相位檢索算法模型，探索了適合整個非干涉光場的相位檢索算法的分類。我們根據(jù)菲涅爾數(shù)[3]將整個衍射光場分為近場、中場和遠場。在衍射光場的近場采用TIE方程來獲取相位的確定解，中場用TIE方程與角譜迭代[4]融合的方法來恢復相位信息，而在遠場直接采用角譜迭代方法來獲取相位信息。實驗證明不同區(qū)域用不同的方法就可以將整個非干涉光場的相位很好的恢復出來。

1 非干涉光場相位恢復算法

1.1 TIE方程與菲涅爾數(shù)

在菲涅爾場相位恢復可以用下面的關(guān)于φ(x,y)非線性完整方程來描述：

方程(2)就是菲涅爾積分，λ=2π/k是波長，U0(x,y)=A(x,y)exp{iφ(x,y)}是物體平面上的未知復振幅，IR(x,y)是測量中在圖像平面z=R處的強度分布值(如圖1所示)。物體平面強度為I0(x,y)≡|A(x,y)|2。

上式(2)可以展開成一個收斂的冪級數(shù)：

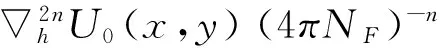
(3)

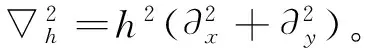
Fr[A,φ,λ,R]≈exp(ikR)[U0(x,y)

(4)

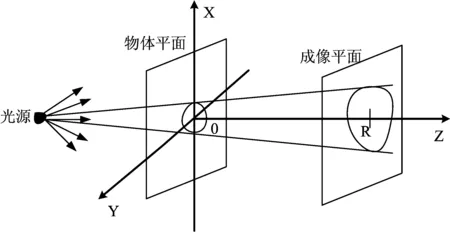
圖1 相位恢復算法實驗示意圖

方程(4)描述了從物體平面z=0到圖像平面z=R之間的自由空間傳播，但是要滿足條件R<

-h·[I0(x,y)hφ(x,y)]?(2πNF)[IR(x,y)]

(5)

方程(5)可以用來求解相位信息，如公式所示，只要知道物體的強度分布I0(x,y)和圖像平面的強度分布IR(x,y)，就可以根據(jù)方程(5)求解相位φ(x,y)。然而，方程(5)是限制在菲涅爾數(shù)NF>>1或傳播距離R<

1.2 角譜迭代算法

根據(jù)平面角譜傳播理論，用U1表示物平面的復振幅函數(shù)：

U1(x1,y1)=ρ1(x1,y1)exp[iφ1(x1,y1)]

(6)

而用U2表示成像平面的復振幅函數(shù)：

U2(x2,y2)=ρ2(x2,y2)exp[iφ2(x2,y2)]

(7)

根據(jù)角譜傳播理論，利用角譜傳遞函數(shù)就可以衍射計算出物平面和像平面光場。該算法在相同條件下，傳播距離越遠效果越好，這點在后面實驗部分會驗證。所以該算法適合衍射光場的遠場相位計算。該算法的初始相位是設(shè)定的隨機相位，在后面的實驗中用到的TIE+角譜迭代算法是用TIE方程解出的相位作為該算法的初始相位。算法的流程圖如圖2所示。

2 整個非干涉光場的相位檢索

2.1 整個非干涉光場相位檢索算法分類

由上述TIE方程推導求解過程可以知道，TIE方程只適合于近場。根據(jù)菲涅爾數(shù)NF來劃分整個衍射光場，再根據(jù)不同相位檢索算法的優(yōu)缺點，將整個非干涉光場的相位檢索分為三類，如表1所示。

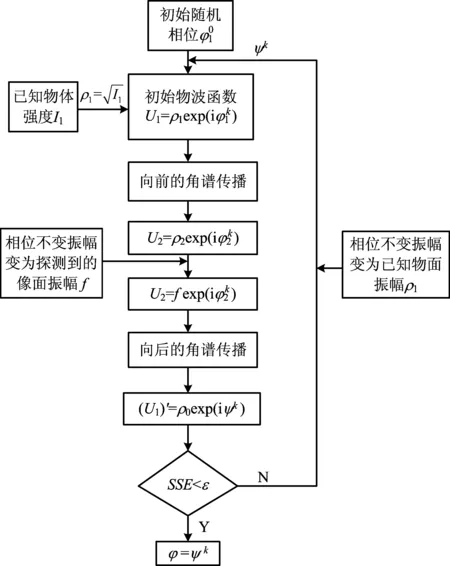
圖2 角譜迭代算法流程圖

Fresnel數(shù)NF遠大于1NF約為1NF遠小于1區(qū)域(物體到圖像的距離)近場(geometric)中間場(Fresnel)遠場(Fraunhofer)相位線性性(圖像對比度的本質(zhì))線性(Laplacian)準線性(hologram)非線性(diffractionpattern)相位恢復方法TIETIE+角譜迭代角譜迭代

2.2 模擬實驗驗證與分析

假設(shè)圖3是物體的相位，其相位值為[-0.45π,0.9π]，采樣間隔h=10-5，波長λ=10-10m，假定物體平面的強度分布是均勻的，即I0(x,y)≡1。整個模擬實驗采用MATLAB軟件仿真實現(xiàn)。

圖3 假想物體相位

2.2.1 近場衍射區(qū)域的相位恢復實驗

近場區(qū)域，NF>>1或z<

圖4 衍射的近場區(qū)域不同距離TIE的恢復結(jié)果

2.2.2 中場衍射區(qū)域的相位恢復實驗

將菲涅爾近場與夫朗和費之間的區(qū)域稱之為中場衍射區(qū)域，即NF≈1，可以求出傳播距離z≈1m。同樣，取1m左右的三個傳播距離：z=0.1m,1m,10m。為了證明在中場采用TIE+角譜迭代方法效果最好，做了三組實驗對比。圖5是在中場使用TIE方程的方法，從結(jié)果來看，傳播距離遠的時候效果很差，與TIE只適合近場的結(jié)論相符，所以該區(qū)域不適合用TIE方程的方法。在同樣的距離情況下單獨用迭代角譜來恢復相位信息，分別迭代100次，可以得到如圖6所示結(jié)果，而且傳播距離越遠效果越好。由于角譜迭代適用于遠場，所以在這個區(qū)域效果不是最好的。

因此，可以將TIE得到的相位作為迭代角譜的初始輸入相位，即采用TIE+角譜迭代的方法，迭代100次，相位恢復的結(jié)果如圖7所示，與上面的圖5和圖6相比較可以看出結(jié)果是最好的。于是，在中場區(qū)域，采用TIE與角譜迭代融合的方法恢復相位信息。

圖5 衍射中場區(qū)域不同距離TIE的相位恢復結(jié)果

圖6 衍射中場區(qū)域不同距離迭代角譜的相位恢復結(jié)果

圖7 衍射中場區(qū)域不同距離TIE+迭代角譜的相位恢復結(jié)果

2.2.3 遠場衍射區(qū)域的相位恢復實驗

在遠場區(qū)域，即夫朗和費區(qū)，NF<<1，可以計算出z>>1m，我們?nèi)∵h遠大于1m的2個距離：z=100m,1000m。TIE方程方法不適合使用，而迭代角譜方法適合遠場區(qū)域，所以用迭代角譜方法迭代100次就可以得到較不錯的結(jié)果，如圖8所示。

圖8 衍射遠場區(qū)域不同距離迭代角譜的相位恢復結(jié)果

綜上所述，模擬實驗證明在不同衍射光場區(qū)域用不同的相位恢復算法就可以將整個衍射光場的相位很好地恢復出來，結(jié)果如圖4、圖7、圖8所示。

2.2.4 兩種算法在時間上的比較

TIE方程的解法只是數(shù)值計算，用MATLAB求解速度較快，而角譜迭代算法收斂速度相對較慢。兩種算法在時間上的比較如表2所示。所以，TIE方程方法在計算時間上占明顯優(yōu)勢而角譜迭代算法相對要犧牲較多的時間。

表2 算法時間比較

3 結(jié)論

非干涉光場的相位恢復算法主要有求解TIE方程和迭代算法兩種，前者適用于衍射近場區(qū)域而后者適用于衍射遠場區(qū)域。兩種算法各有缺點，為了得到更好的結(jié)果也可以將兩者結(jié)合起來，即將求解TIE方程得到的相位值作為迭代算法的迭代初始值。筆者從整個非干涉光場角度出發(fā)，討論了適合整個非干涉光場的相位檢索的算法模型，而且用模擬實驗驗證了該算法模型，該算法模型對整個衍射場的相位都作出了很好的恢復。

參考文獻：

[1]K.A.Nugent.The Measurement of Phase through the Propagation of Intensity: an Introduction[J].Contemporary Physics,2011,52(1):55-69.

[2]M.R.Teague Deter.Ministic Phase Retrieval: a Green’s Function Solution[J].J Opt Soc Am, 1983(73):1434-1441.

[3]黃利新，姚新，蔡冬梅，等.一種快速高精度的相位恢復迭代法[J].中國激光，2010，37(5)：1218-1221.

[4]程鴻，章權(quán)兵，韋穗，等.基于強度傳輸方程的相位檢索[J].光子學報，2011，40(10)：1566-1570.

[5]王瀟，毛珩，趙達尊.基于光強傳播方程的相位恢復[J].光學學報，2007，27(12)：2117-2121.

[6]J.R.Fienup.Phase Retrieval Algorithms: A Comparison [J].Appl.Opt,1982(21): 2758-2769.

[7]程鴻，沈川，張成，等.強度傳輸方程和角譜迭代融合的相位檢索算法[J].中國激光，2014(6)：187-192.