CDC—代數(shù)上中心化映射的刻畫

馬 飛，趙健堂，鄭 欣

設(shè)A是一個環(huán)或代數(shù)，若可加映射φ:A→A滿足 ?a,b∈A ，有 φ(ab)=φ(a)b(φ(ab)=aφ(b))，則稱 φ是一個左(右)中心化子。既是左中心化子又是右中心化子的映射稱為中心化子；?a∈A,有φ(a)a-aφ(a)∈Z(A)(Z(A)為 A的中心)，則稱φ是中心化映射;如果φ(a)a=aφ(a),則稱映射φ可交換。

關(guān)于映射在哪些條件下是中心化子一直是國內(nèi)外學(xué)者們研究的熱點問題。如在文獻[1]中證明了半素環(huán)R上的映射φ既是左、右Jordan中心化子是中心化子；文獻[2]中研究了特征不為2的自由半素環(huán) R上的可加映射 φ若滿足 ?a∈R，有2φ(a2)=φ(a)a+aφ(a)，則 φ 是中心化子；文獻 [3]中證明了特征不為2的素環(huán)上的可加映射φ,若滿足?a∈R,n≥2都有φ(an)=φ(a)an-1,那么φ是左中心化子；文獻[4-5]也研究了相關(guān)內(nèi)容，并最終得到了標準算子代數(shù)上滿足φ(Am+n+1)-Amφ(A) An∈FI(其中m,n為正整數(shù))，則存在數(shù)域F中的常數(shù)λ,使得對任意的a∈A,有φ(a)=λa。我們在文獻[6]的基礎(chǔ)上中將齊霄霏的結(jié)果推廣到了任意的完全分配可交換子空間格代數(shù)上。

1預(yù)備知識

下面我們來介紹幾個與本文證明有關(guān)的引理：

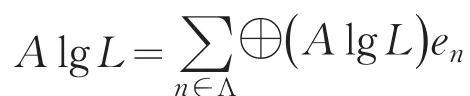
引理2[10-11]設(shè)A lg L是Hilbert空間H上的不可約CDC-代數(shù)，則存在一個非平凡投影e∈L，使得e(A lg L) e⊥是忠實的A lg L-雙邊膜。即對于任意的 A∈A lg L，如 果 Ae(A lg L) e⊥={0} ，則 有Ae=0；如果e(A lg L) e⊥A={0} 成立，則有e⊥A=0。

從文獻[12]中可知，CDC-代數(shù)由其本身所包含的秩一算子弱*閉生成的；而文獻[10-11]分別探究了線性導(dǎo)子以及線性Lie導(dǎo)子、CDC-代數(shù)上的代數(shù)同構(gòu)。在CDC-代數(shù)A lg L中，設(shè)U(L)={e∈L：e≠0,e-≠H } ，若存在e1，e2，…，en∈U(L )，使得ei與ei+1可比，e0=e，en+1=e'(i=0，1，…，n )，那么就稱U(L ) 中的e，e'是連通的。存在C?U(L)，如果C中的任意兩個元素都是連通的，并且C中的任意一個元素與U(L)C都不連通，那么就稱C為U(L)的連通分支。令L是復(fù)可分的Hilbert空間H上的一個完全分配的交換子空間格。由于當且僅當A lg L的交換子是平凡的時候，A lg L是不可約的，即A lg L的一次換位是FI，也算子為I。……