基于改進人工蜂群算法的支持向量機時序預測*

劉 棟, 李 素, 曹志冬

(1.北京工商大學 計算機與信息工程學院 食品安全大數據技術北京市重點實驗室,北京 100048; 2.中國科學院 自動化研究所 復雜系統管理與控制國家重點實驗室,北京 100190)

0 引 言

支持向量機(support vector machine,SVM)[1]，有效克服了非線性、過學習和局部極小值等問題;在眾多領域的理論分析和實際應用中取得巨大成功，一度被公認為是機器學習領域的最佳算法。核參數尋優對于SVM具有決定性影響，現有優化方法[3～5]仍存在難以規避的問題。相比其他智能算法，人工蜂群[6](artificial bee colony ,ABC) 算法獨有角色分工轉換機制能平衡算法的全局和局部搜索，較大程度地擺脫局部最優，增大全局最優解的獲取機率，且算法易實現、搜索精度高、控制參數少、魯棒性強，但受限于自身進化方式和選擇策略，實際應用中有待進一步加強[6，7]。粒計算是海量信息處理的一種新的計算范式，使大數據背景下復雜性、模糊性問題及滿意近似解的研究逐漸成型，如模糊信息粒化理論[8](theory of fuzzy information granulation,TFIG)。

本文通過改進各分工蜂群的搜索機制進行SVM參數尋優，并引入信息粒化技術進行上證指數變化趨勢和變化空間的建模預測來證明所提出方法的優越性。

1 支持向量回歸

(1)

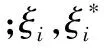
(2)

式中K(xi,x)為核函數，在線性不可分的情況下引入。

2 經典ABC算法

設原問題解空間維數是D，j∈{1,2,…,D}。搜索開始，引領蜂根據式(3)進行領域搜索并更新食物源位置

vij=xij+φ(xij-xkj)

(3)

式中j為隨機整數，k∈{1,…,NP}且k≠i，代表從NP個食物源中隨機選取一個不等于i的食物源，φ～U(-1,1)決定xij鄰域的取值范圍。當新食物源Vi=[vi1,…，vij]優于Xi，貪婪選擇將Vi代替Xi；否則，保持Xi不變。待所有引領蜂已完成搜索和更新，立即進入信息交換區以搖擺舞的方式分享食物源信息。跟隨蜂根據既得食物源信息，參照一定概率Pi并按輪盤賭來選擇跟隨引領蜂，首先在區間[0,1]上生成一個服從均勻分布的隨機數r，若Pi>r，按式(3)進行鄰域搜索，并以與引領蜂相同的貪婪選擇策略確定要保留的食物源(或解)

(4)

式中fiti為解的適應度值評價，通常為最小化優化問題

(5)

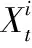
3 基于改進ABC算法的TFIG-SVR框架

3.1 經典ABC算法的改進

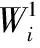
(6)

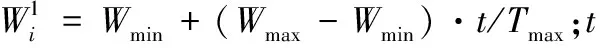
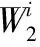
(7)

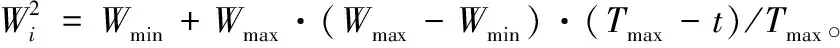
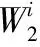
3.2 TFIG-SVR技術優越性的理論推導

對SVM引入TFIG構建TFIG-SVR，并進行幾何論證：1)基于原始樣本空間進行粒劃分并在每個粒上進行支持向量訓練,實現將非線性問題轉化為若干線性可分問題,來獲得一系列決策函數；2)這種學習策略增強了模型的泛化能力和擬合精度，有利于回歸預測[9，10]；如圖1，傳統SVR將整個樣本特征空間用一個連續回歸超平面F擬合，而GSVR則把特征空間劃分為一系列子空間,然后基于子空間構建SVR來獲得回歸超平面F*，根據統計學及不敏感損失函數理論，F*相比F具有間隔更寬的超平面。因此，GSVR機制增強了模型的擬合精度，降低了算法時間復雜度，抑制過學習而獲得了更強的泛化能力，另外，擬合過程的可并行實現又進一步提高了學習效率。其中，三角型模糊粒子可用于多決策性問題，因此,本文采用Pedrycz W所提出的三角形模糊集信息粒化方法[11]來構建TFIG-SVM模型。

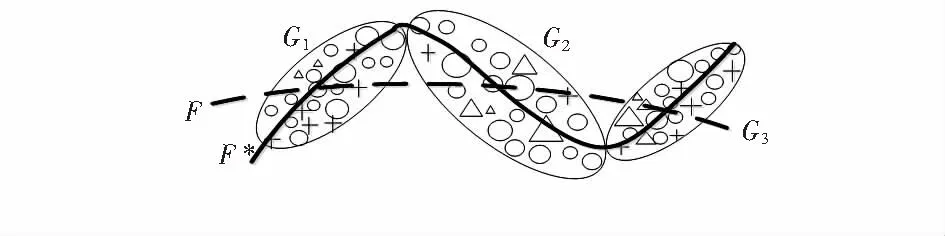
圖1 TFIG-SVR擬合示意

3.3 TFIG-SVR設計

文獻[2,3,9,10,12]表明：高斯核即徑向基核函數(radial basis function,RBF)，具有優良的非線性擬合性能，其參數包括：σ表征核的寬度(核函數徑向作用范圍)；C控制分類或回歸超平面復雜程度和異常點數間的平衡，影響模型泛化性能；ε描述決策函數對預測誤差不敏感區域的寬度，即真實值與預測值的差落在預定區間內，則認為無損失；反之，則有損失。本文采用改進ABC算法對SVR進行參數優化，并將SVR預測值的均方誤差作為目標函數：minf(C,σ,ε)，得TFIG-SVR及其算法流程如圖2。

1)參數初始化。ABC算法基本參數設置、最大、最小慣性權重Wmax和Wmin以及適應度函數如式(5)，fi為預測值與真實值的均方根誤差； SVR相關參數元組(C,σ,ε)。

2)引入Pedrycz W模糊粒化方法處理原始數據，使Low,Mean,Up為三角型模糊粒子的參數,代表樣本數據變化趨勢的支撐下限、核和支撐上限。

3)利用改進ABC算法進行參數尋優。將參數三元組(C,σ,ε)抽象為食物源，通過C，σ和ε取值重新初始化蜂群，使引領蜂和跟隨蜂按式(6)和式(7)搜索，并按經典ABC算法步驟執行和跳轉，直到滿足算法結束條件，來獲得最佳參數元組(C,σ,ε)best，嵌入SVR對粒化數據進行回歸預測。

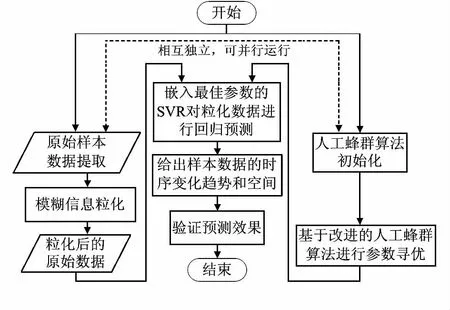
圖2 基于改進人工蜂群算法的TFIG-SVR

3.4 模型時間復雜度計算

本文將構建網格搜索(gridsearch)[2]、粒子群優化(PSO)算法[3]、遺傳算法(GA)[4]、蟻群優化(ACO)算法[5]和人工蜂群算法的SVR模型(設為x-SVR表1作為對照實驗，將SVR時間復雜度統一設為定值O(f(n))，那么x-SVR時間復雜度僅須比較其核心智能算法。其中采用文獻[2]中網格搜索算法，其時間復雜度可粗略估計為O(n3)。設NCircle為進化代數，n為種群規模，D為決策變量的維數，當n→D得表 1。其中，改進ABC算法時間復雜度與D無關僅取決于n；如果n足夠大，低次冪項可忽略，那么改進ABC算法與其經典算法相比，幾乎不需要額外付出時間耗費，另外，蟻群算法時間復雜度最高。

表1 x-SVR模型時間復雜度比較

4 實例應用與分析

收集上證指數1990年12月19日～2016年1月14日所有交易數據，包括收盤指數、指數最高值、指數最低值、當日交易量、當日交易額，預測后續5個交易日收盤指數的變化趨勢和變化空間如表2。

表2 2016年1月15日至2016年1月21日上證實際收盤指

4.1 實驗參數設定

1)gridsearch-SVR的懲罰參數C和核參數γ的設定，學術界并未明確限定，但C過高會陷入過學習，所以,本實驗設定為[-8,8]和[-8,8](取以2為底的冪指數值)，步距為1，相當于進化兩代；2)考慮到樣本數據規模較大，將PSO-SVR、ABC-SVR、改進ABC-SVR、GA-SVR和ACO-SVR相同參數設置為：種群進化代數為200，種群規模為20，損失函數ε的取值范圍為(0,1]，核函數相關參數γ的取值范圍為(0,1]，罰參數C的取值范圍(0,100]，其余參數均按算法最優性能設定；3)權重參數設定，最大慣性權重Wmax和最小慣性權重Wmin參照文獻[13]設定。

4.2 實驗結果分析

將引入TFIG的PSO-SVR、ABC-SVR、改進ABC-SVR、GA-SVR和ACO-SVR用于上證收盤指數預測，得到x-SVR模型2016年1月15日～21日收盤指變化空間結果如表 3。改進ABC-SVR預測所得收盤指數變化空間與表2中實際收盤指數最為接近，其次是PSO-SVR，ABC-SVR，GA-SVR，gridsearch-SVR，ACO-SVR表現最差，甚至產生了支撐預測空間支撐下限大于支撐上限的預測錯誤。

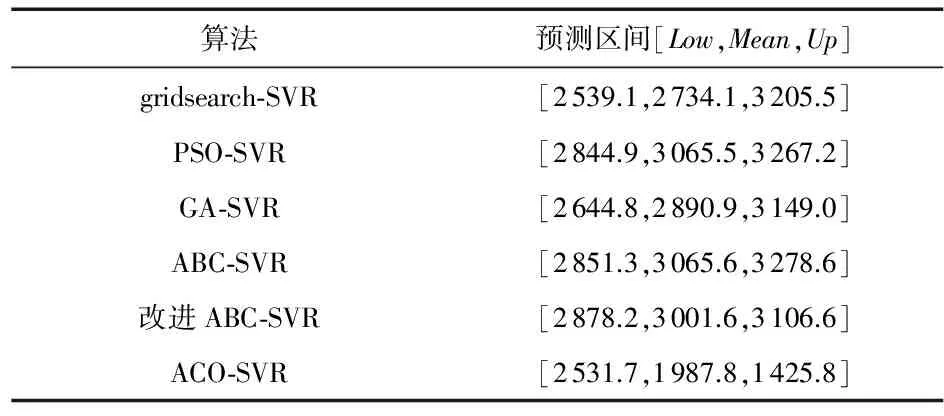
表3 x-SVR模型最終預測結果比較

上限參數Up是證券收盤指數預測最為核心的評價指標，由圖3上限參數Up預測值的均方根誤差隨進化代數的變化可看出，ACO-SVR產生的誤差值最大，預測精度不高，相比其他預測模型存在較大差距，說明蟻群算法不適合連續型時間序列預測與分析。改進ABC-SVR均方根誤差最小，預測精度最高，其次依次為PSO-SVR，ABC-SVR，GA-SVR。在收斂速率上，PSO-SVR在算法早期率先達到穩定狀態，但后期收斂速率變慢；GA-SVR相對于其他算法明顯早熟，進化40代后進入成熟狀態，對新空間的探測能力極為有限，且模型不穩定，易陷入局部最優；而改進的ABC-SVR和ABC-SVR初期算法進化過程相似，但改進ABC-SVR比ABC-SVR收斂速度更快，預測精度更高，且更早成熟。

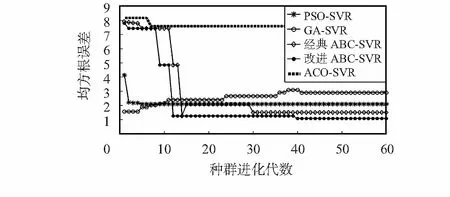
圖3 上證收盤指數預測迭代

為進一步對比x-SVR性能，基于主頻2.7 GHz實驗平臺的MATLAB R2012b上運行程序，得到x-SVR的實際運行時間(s)和參數Up的預測平均絕對百分比誤差(MAPE)如表 4，x-SVR運行時間與表1中對于x-SVR時間復雜度的公式推導結果完全吻合。如表4，智能算法中改進ABC-SVR和PSO-SVR模型訓練速率明顯快于ABC-SVR和GA-SVR；預測精度方面，改進ABC-SVR進化40代時就已經明顯超過其他所有模型進化200代所能夠達到的預測精度，且運行時間和網格搜索接近；另外，網格搜索回歸精度與ABC-SVR接近，但運行時間不到ABC-SVR的1/4，網格搜索算法擁有進一步改進的潛力，表明：大數據條件下，簡單模型往往具有更強的泛化能力和回歸效能，如網格搜索法。

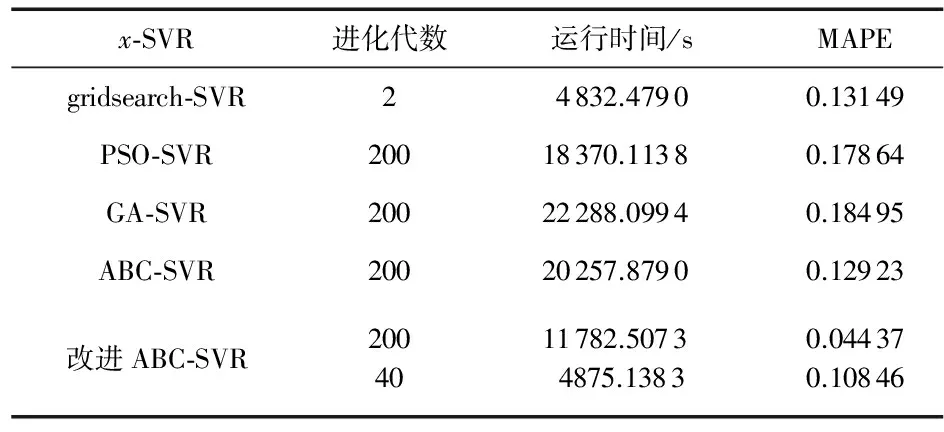
表4 x-SVR模型效能對比

5 結 論

1)繼承經典ABC算法技術優勢，同時提高了其收斂速率和預測精度；2)所提出算法在進化40代在回歸精度和預測性能上可以明顯超過其他智能算法，該方法對諸如關注效率和性能的數據樣本也具有良好的通用性和可借鑒性；3)能在一定程度上擺脫局部最優和早熟限制，具有良好的泛化性能；4)與基線實驗網格搜索模型相比，即使在算法時間耗費方面，算法進化40代達到可接受精度的前提下運行時間與大規模樣本數據下的簡單模型接近，5)以模糊信息粒化技術進行變化空間和趨勢預測，規避了復雜結構數據難以追求問題最優解及定量化精確描述的困局。

參考文獻:

[1] Chapelle O,Vapnik V,Bousquet O,et al.Choosing multiple parameters for support vector machines[J].Machine Learning,2002,46:131-159.

[2] Ma X Y,Zhang Y B,Wang Y X.Performance evaluation of kernel functions based on grid search for support vector regression[C]∥The 7th International Conference on Cybernetics and Intelligent Systems & IEEE on Robotics,Automation and Mechatronics,2015:283-288.

[3] Xiao T J,Ren D,Lei S H,et al.Based on grid-search and PSO parameter optimization for support vector machine[C]∥The 11th World Congress on Intelligent Control and Automation,2014:1529-1533.

[4] 崔小勇,林 寧.基于遺傳模擬退火算法的無線傳感器網路由協議[J].傳感器與微系統,2016,35(7):32-34.

[5] 倪 壯,肖 剛,敬忠良,等.改進蟻群算法的飛機沖突解脫路徑規劃方法[J].傳感器與微系統,2016,35(4):130-133.

[6] Basturk B,Karaboga D.An artificial bee colony(ABC)algorithm for numeric function optimization[C]∥Proceedings of IEEE Swarm Intelligence Symposium,Indianapolis,USA,2006:651-656.

[7] Karaboga D,Basturk B.A comparative study of artifieal bee colony algorithm[J].Applied Mathematics & Computation,2009,2(14):108-132.

[8] Zadeh L.Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic[J].Fuzzy Sets Syst,1997,90:111-127.

[9] 徐 計，王國胤，于 洪.基于粒計算的大數據處理[J].計算機學報,2015,38(8):1497-1517.

[10] Wang W J,Guo H S.Granular support vector machine based on mixed measure[J].Neurocomputing,2013,101(3):116-128.

[11] Pedrycz W.Knowledge-based clustering-fromdata to information granules[M].New Jersey:John Wiley & Sons,Inc,2005.

[12] Cheng X,Guo P.Short-term wind speed prediction based on support vector machine of fuzzy information granulation[C]∥25th Chinese Control and Decision Conference,CCDC 2013,2013:1918-1923.

[13] Nickabadi A,Ebadzadeh M M,Safabakhsh R.A novel particle swarm optimization algorithm with adaptive inertia weight[J].Applied Soft Computing,2011,11(4):3658-3670.