基于SPH法的冰與船舶螺旋槳碰撞數值模擬

桂洪斌 ， 胡志寬 ，2

（1.哈爾濱工業大學（威海），山東 威海 264209；2.中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

在我國渤海和黃海北部海域，每年入冬均有大量海冰，冰對船舶與海洋結構物的作用和影響一直受業界的重視。船舶在結冰海區航行時，其螺旋槳裸露在船尾，并且浸入水中深度較淺難以避免與冰發生相互作用，使得槳葉葉梢及葉緣等區域遭受嚴重的損傷[1]。螺旋槳與冰相互作用主要有兩種形式，分別為螺旋槳對冰塊（層）的銑削作用和冰塊對螺旋槳的沖擊作用[2]。銑削作用是在有較大冰塊或者冰塊困在船體和螺旋槳之間的情況下發生的，此時螺旋槳如同銑削冰塊，其產生的負載對螺旋槳槳葉損傷很大。冰沖擊現象則是由小尺寸的冰塊撞擊槳葉引起，且較頻繁產生。目前在規范[1，3]中，僅給出螺旋槳與冰相互作用時最大靜冰力的計算公式及冰況，主要用于冰區加強型螺旋槳的結構設計以及靜力校核等[4]。而冰塊對螺旋槳的沖擊作用，即冰—槳碰撞問題，是一種瞬態動力響應問題，我國對該問題的研究還非常缺乏。對于此類碰撞動力問題，由于實驗代價極高，數值模擬成為冰—槳碰撞研究的一種重要方法。

有限元方法是研究冰與結構物作用的一種重要數值模擬方法。目前，有限元軟件如ANSYS/LSDYNA、MSC.DYTRAN等均可用于結構物之間動力作用的數值仿真中，如用ANSYS/LS-DYNA模擬冰與錐體抗冰結構的動力作用過程[5]；用MSC.DYTRAN模擬浮冰撞擊LNG船的碰撞過程[6]等。上述冰與錐體結構或LNG船的碰撞均為低速碰撞，而冰與螺旋槳碰撞時，冰塊是以很大的相對速度撞擊槳葉，給槳葉造成嚴重的損壞。同時，在高速撞擊的過程中，冰將以高的應變率表現為脆性破壞和極端大變形。冰—槳碰撞同鳥撞[7-8]、冰雹沖擊問題類似，國內外學者針對鳥撞和冰雹沖擊問題均開展了大量的研究工作，主要集中在實驗方法和數值模擬方法兩個方面。在處理鳥撞和冰雹沖擊等高速碰撞問題時，鳥體或冰雹往往會出現極度大變形現象，有限元方法在求解這些工程問題時就變得相當困難。

通過查閱文獻，Anghileri等[9]采用Lagrange（拉格朗日）、ALE（任意朗格朗日—歐拉）和SPH（光滑粒子流體動力學）三種方法對冰雹沖擊鋁板進行了數值模擬和對比。Pernas[10]采用Carney[11-12]等的實驗模型，在數值模擬中將冰的數值模型采用自定義本構子程序，基于Lagrange、ALE和SPH三種方法進行數值模擬，其分析結果與Carney的實驗數據進行了比對。以上研究發現，基于SPH法的模擬結果較于Lagrange和ALE法更貼切試驗結果，計算效率更高，更能較真實模擬結構的極端大變形。SPH法是較突出的一種無網格數值方法，其優點在于它是一種純Lagrange方法，可避免高維拉式網格方法中的網格纏繞、扭曲、負體積等問題，避免Euler方法難于追蹤物質變形的缺點，也避免了ALE方法不斷重構網格并增加計算時間的缺點，所以適用于冰—槳碰撞問題中冰的動態大變形模擬。

因此，本文建立了冰—槳碰撞計算模型，基于冰高速撞擊槳葉的脆性變形特點，冰模型采用SPH法，槳葉模型采用有限元Lagrange方法，運用非線性有限元軟件ANSYS/LS-DYNA，對螺旋槳與冰在不同速度和位置下碰撞和螺旋槳與不同半徑冰碰撞下的動態響應進行了研究。

1 冰的數值模型及驗證

1.1 冰的數值模型

真實的海冰材質復雜，其本構關系難以描述，并且在撞擊槳葉過程中呈現極端大變形現象，導致在碰撞分析中難以對冰建立準確的數值模型。高速沖擊下的冰，會涉及到高應變率的問題，冰在應變率增加時會經歷一個由韌性轉為脆性破壞的轉變過程[12]。如何能夠較準確模擬冰的失效破壞和確保結構響應的可參考性，冰的數值模型尤為關鍵。由于冰材質的復雜性，往往在數值模擬中假定冰是一種典型的彈塑性材料，本研究采用Carney等提出的帶有失效模式的高應變率的冰數值模型。冰的材料模型采取各向同性彈塑性材料模型，即LS-DYNA材料庫中的MAT155（關鍵詞為*MAT_PLASTICITY_COMPRESSION_TENSION_EOS），材料參數、狀態方程以及冰的應變率靈敏度等設置參照文獻[12-14]。

1.2 高速冰沖擊驗證

為了驗證冰的數值模型和碰撞數值模擬計算方法的可行性，本文參照Carney的實驗沖擊模型如圖1所示，即直徑為17.46 mm、長度為42.16 mm的冰柱以一定的速度沖擊直徑為63.5 mm、長度為19.05 mm的鋼柱。在建模過程中，需要特別注意彈簧單元和集中質量單元的建立，彈簧K1、K2、K3的剛度系數和集中質量M在圖1已給出。鋼柱采用有限元Lagrange網格，假定為剛體（關鍵字為*MAT_RIGID，只允許縱向位移），密度為8 000 kg/m3，彈性模量為193 GPa，泊松比為0.29。冰模型采用SPH法，SPH模型的建立通過LS-DYNA后處理器LS-PREPOST進行，其單元數為35 800個。冰的沖擊速度分別設置為91.44 m/s，152.40 m/s和213.36 m/s。接觸算法采用自動點對面接觸，時間步長取為0.5。為了便于精確地提取彈簧力時程曲線和輸出更多的計算節點，在*DATABASE_OPTION的DEFORCE選項中DT設置為5e-9。另外，彈簧K3的最下端采用剛性固定，彈簧與彈簧、質量、鋼柱的連接方式采用共節點形式。計算截止時間為0.2 ms。

最終SPH-FE模型如圖2所示。通過對K文件進行求解后，提取彈簧K1的彈簧力時程曲線，對數據進行過濾（濾波頻率為25 kHz）。圖3分別列出了本文計算的沖擊速度為91.44 m/s，152.40 m/s和213.36 m/s下彈簧K1力隨時間變化曲線，并與Carney的實驗數據等相對比。在0-0.2 ms內，本文計算的數值模擬結果與Carney的實驗結果和數值模擬結果吻合較好，同時也驗證了冰的數值模型及碰撞計算方法的可行性。圖4所示為冰在沖擊速度為152.40 m/s下0-0.2 ms內部分時刻沖擊示意圖，由圖中可見冰在高速沖擊時出現的極端大變形和粉碎性撞擊現象。

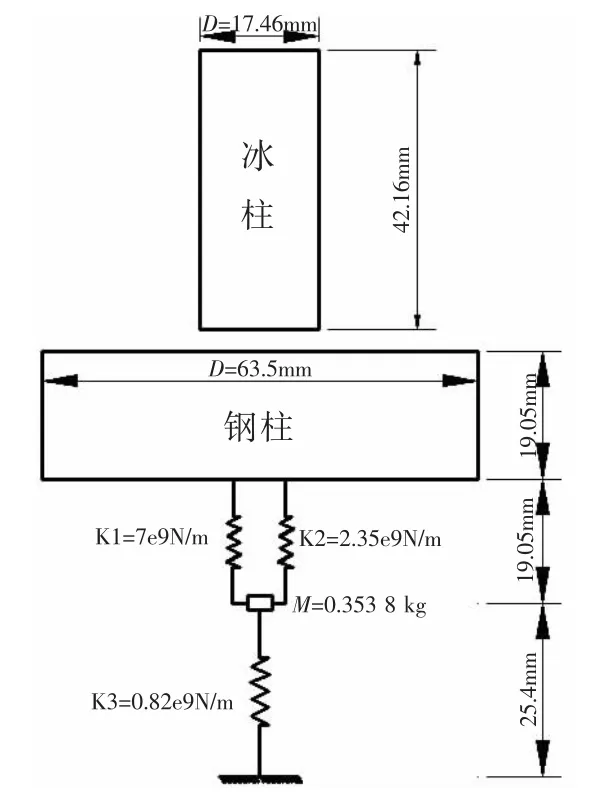
圖1 沖擊模型示意圖Fig.1 Impact model

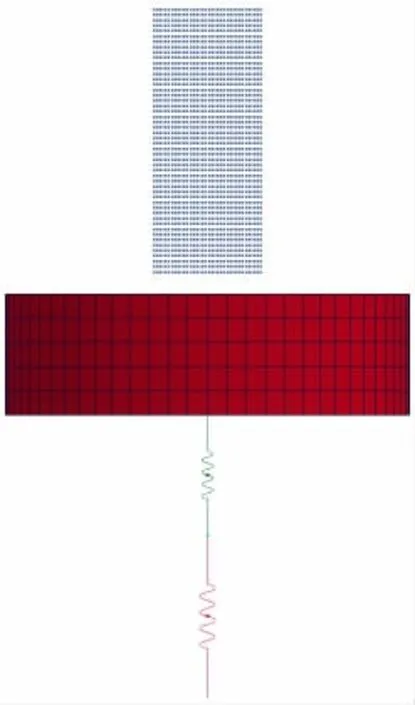
圖2 SPH-FE模型Fig.2 SPH-FE model

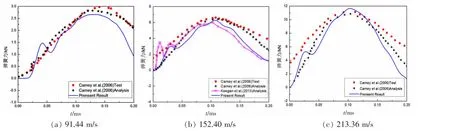
圖3 彈簧K1力時程曲線對比圖Fig.3 Spring K1force history results

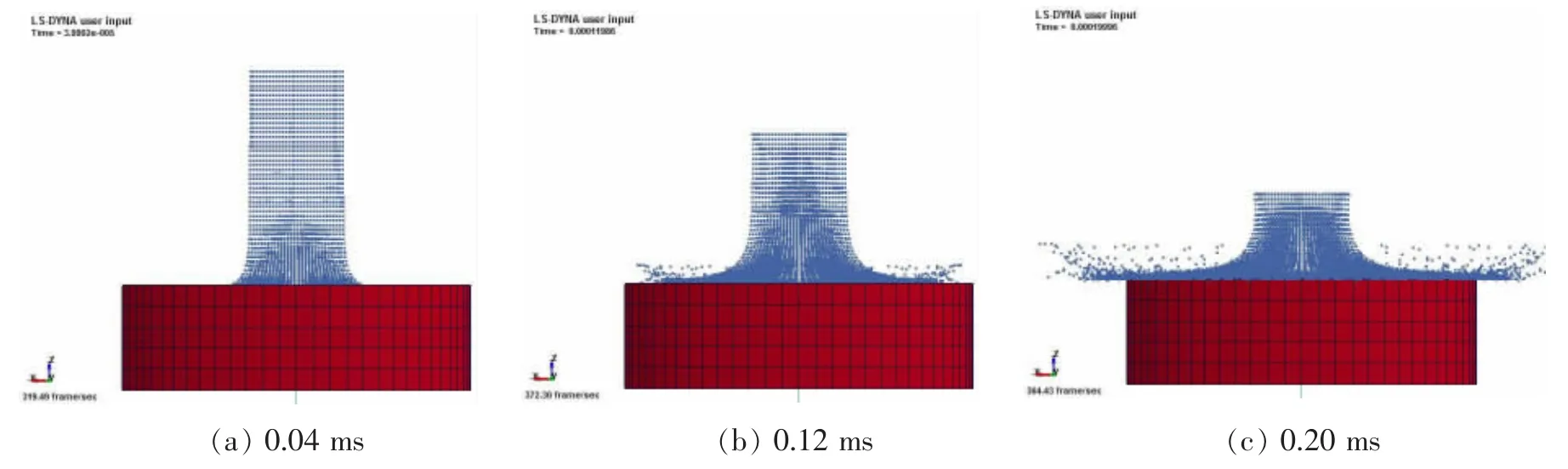
圖4 部分時刻沖擊示意圖（沖擊速度為152.4 m/s）Fig.4 Part time impact diagram(velocity：152.4 m/s)

2 冰—槳碰撞的動態響應分析

2.1 冰—槳碰撞的影響因素

冰—槳碰撞過程極其復雜，槳葉損壞的程度主要取決于螺旋槳的幾何型式及材料屬性、冰塊與螺旋槳的碰撞部位及相對速度、冰塊幾何形狀及尺寸、冰的物理力學特性以及海水流體環境等。由于上述涉及到的因素復雜且多具有不確定性，本文忽略海水流體環境和冰塊幾何形狀等影響，冰塊假定為球體。根據運動的相對性，假定槳葉不轉動，則冰塊以高速撞擊槳葉，主要考慮相同條件下分別改變冰-槳碰撞速度、位置以及冰的半徑單個碰撞參數，對比研究不同碰撞工況下槳葉的變形、單元最大應力以及碰撞過程中產生的碰撞力等響應差異。

2.2 冰—槳碰撞模型建立

槳葉模型的設計參數來源于某沿海單槳散貨船螺旋槳，其主要設計參數和材料屬性如表1所示。槳葉模型采用有限元Lagrange網格，如圖5所示，單元類型選用10節點四面體Solid168單元，單元數為26 281。約束條件是在槳葉0.2R半徑處，即葉根處設定為固定約束。冰采用SPH模型，如圖6所示，材料參數的設置同本文1.2節。計算終止時間為6 ms。

表1 槳葉設計參數及材料屬性Tab.1 Design parameters and material properties of blade

圖5 槳葉有限元模型Fig.5 Finite element model of blade

圖6 冰SPH模型Fig.6 SPH model of ice

2.3 冰—槳碰撞速度的影響

對于冰-槳碰撞問題，其相對速度是一個很重要的因素。假定半徑r為0.10 m的冰球撞擊槳葉葉面的0.975R附近區域（葉梢部位）這一碰撞模型，冰的沖擊速度方向為螺旋槳的前進方向（沿Z軸正向），速度大小分別為 5 m/s、10 m/s、20 m/s、30 m/s、40 m/s和 50 m/s。

圖7和圖8所示分別為碰撞速度為50 m/s時部分時刻冰和槳葉的變形云圖，可見冰在碰撞過程中受到擠壓發生大變形，其變形情況遠遠大于槳葉的變形情況，主要是因為冰的彈性模量和密度均比螺旋槳小得多。由圖8可見，槳葉的最大變形處位于碰撞區域的葉梢部位附近，為了便于觀察槳葉的變形，選取葉梢部位的節點348，節點位置如圖9所示。不同碰撞速度下該節點的位移時程曲線如圖10所示，可見，隨著碰撞速度的增大，同等時刻下，槳葉的變形也增大。

圖11給出了冰以不同碰撞速度下撞擊槳葉的碰撞力隨時間的變化曲線。從圖11可以看出，碰撞速度越大，其碰撞越劇烈，冰與槳葉越開始接觸碰撞，產生的碰撞力越大，碰撞力進入峰值的時間越短。同樣，槳葉單元最大應力和最大應變隨時間變化曲線分別如圖12和圖13所示，可見，碰撞過程中短時間內會給槳葉巨大的沖擊力，使得槳葉的最大應力和最大應變均迅速增大，并且在同一時刻，碰撞速度越大，槳葉的最大應力和最大應變均越大。

為了更好地觀察槳葉局部單元應力的情況，選取葉背表面的單元10016、13824、24824、20463和19420，各單元位置如圖9所示。圖14給出了碰撞速度為50 m/s時五個單元的應力時程曲線并與槳葉所有單元的最大應力時程曲線對比圖。由圖14可以看出，在0-1.0 ms內，單元10016的應力接近槳葉所有單元的最大應力時程曲線，說明槳葉的最大應力的區域位于單元10016附近的葉梢部位；同樣，在1.5-3.0 ms內，單元13824的等效應力時程曲線接近槳葉所有單元的最大應力時程曲線，這說明在該時間內，槳葉的最大應力處位于單元13824附近的局部區域。以此類推，最大應力值的區域是隨著碰撞時間的改變而變化的，隨著時間的增加，最大應力值的區域將從葉梢部位逐漸向葉根部位轉移。

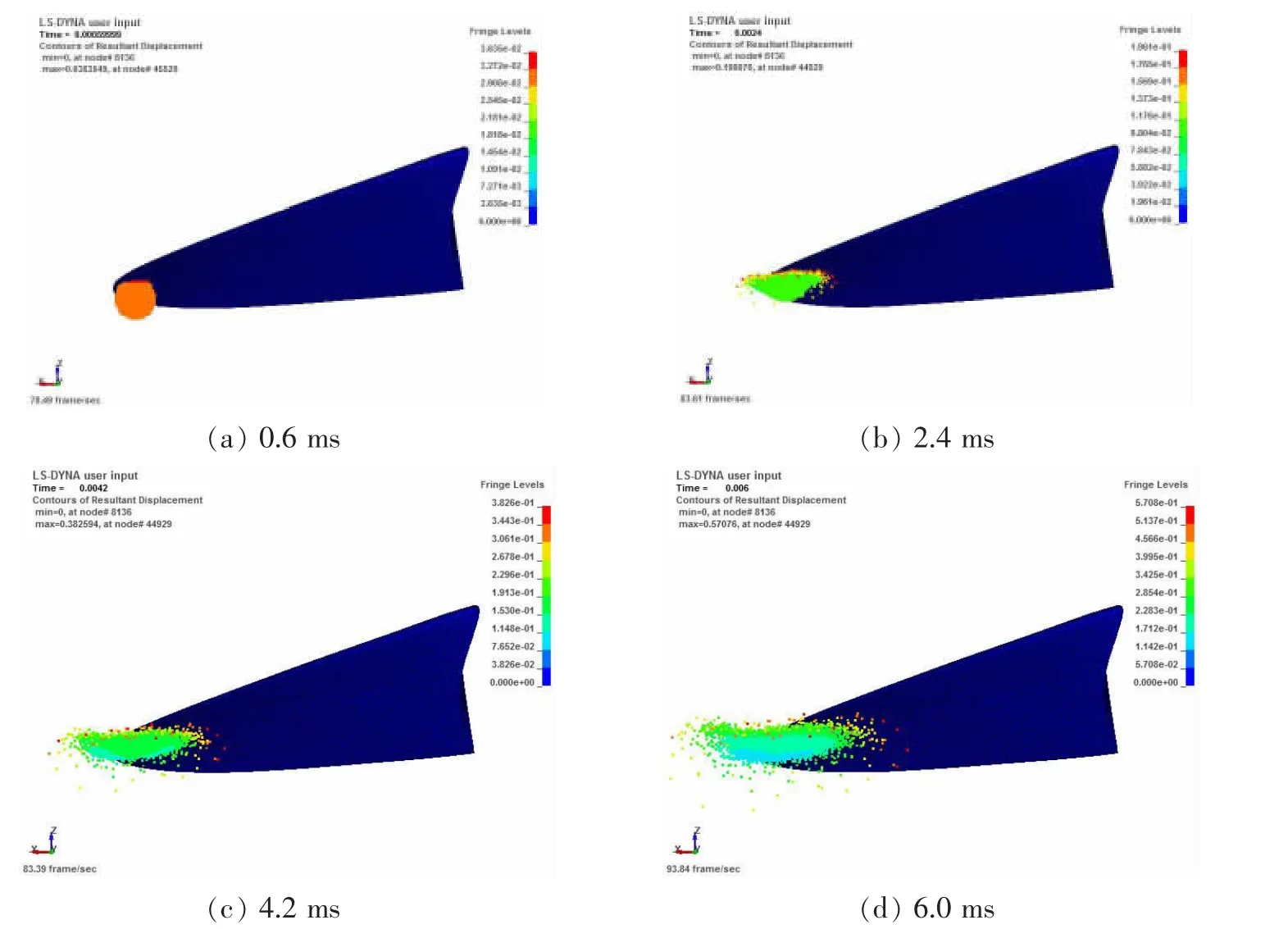
圖7 部分時刻下冰的變形云圖（V=50 m/s）Fig.7 Part time deformation of ice(V=50 m/s)

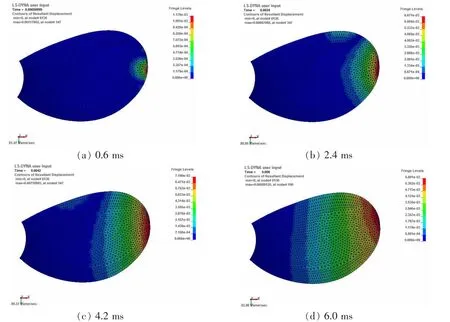
圖8 部分時刻下槳葉的變形云圖（V=50 m/s）Fig.8 Part time deformation of blade(V=50 m/s)

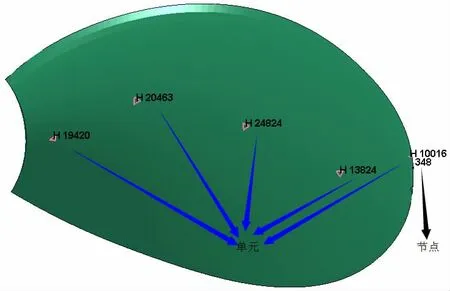
圖9 選取節點和單元位置Fig.9 Location of selected node and elements

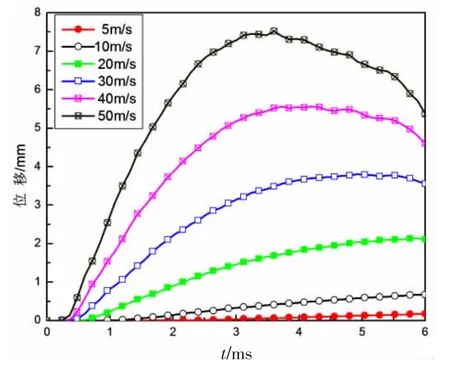
圖10 節點348位移—時間曲線Fig.10 Node 348 displacement-time curves

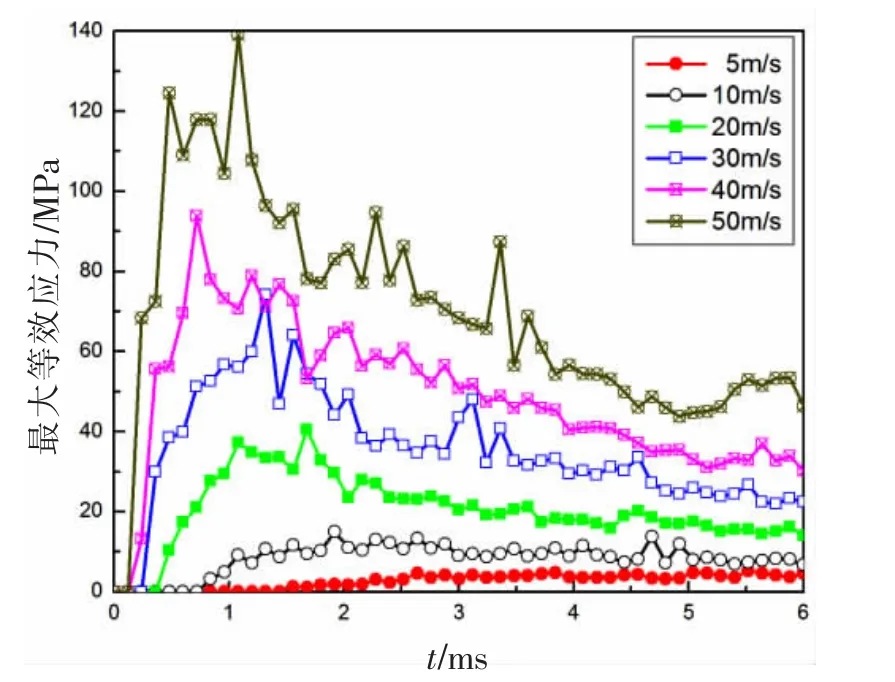
圖12 槳葉單元最大應力—時間曲線Fig.12 Blade elements maximum strain-time curves

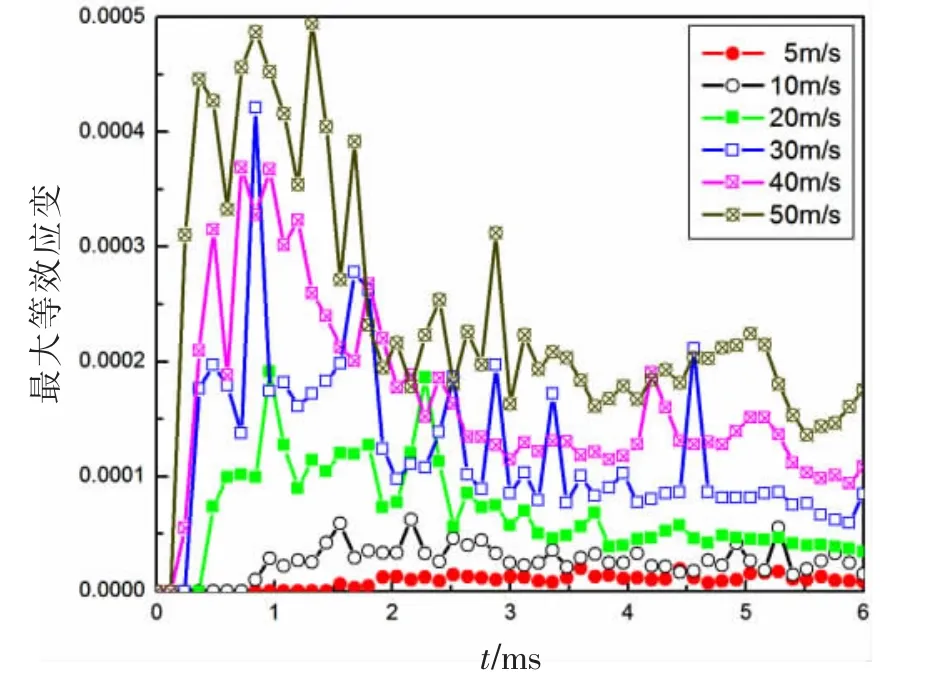
圖13 槳葉單元最大應力—時間曲線Fig.13 Blade elements maximum stress-time curves

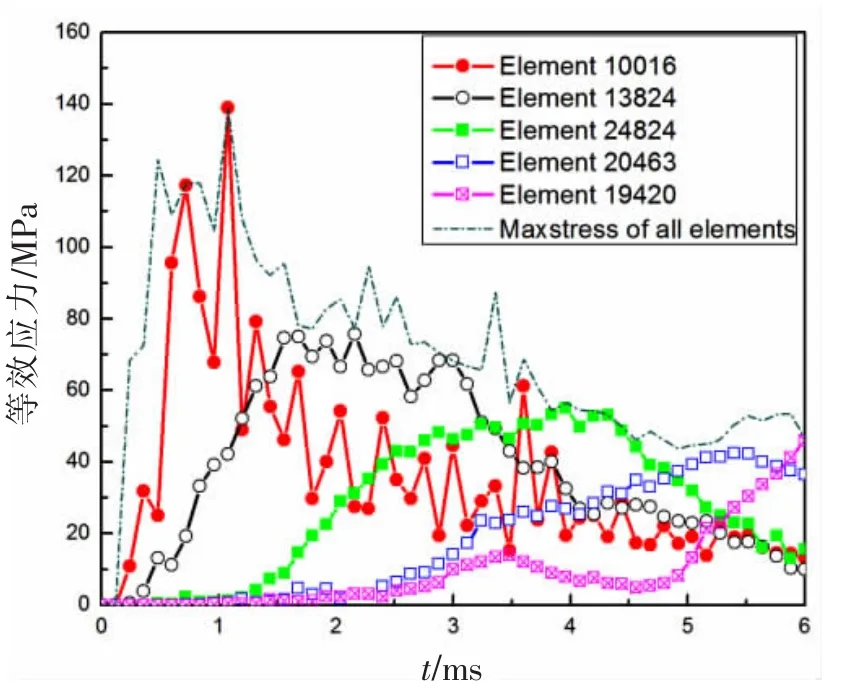
圖14 選取單元應力—時間曲線Fig.14 Elements selected maximum stress-time curves

2.4 冰—槳碰撞位置的影響

螺旋槳不僅其曲面高度不規則，而且其厚度各處均不同，使得冰與槳在不同位置發生碰撞時，冰對槳葉的損傷情況不同。顯而易見，在相同條件下，槳葉較薄的葉緣區域受到撞擊時，最容易受到損害。本文將對表2的三種碰撞計算工況進行模擬和分析。冰的沖擊速度方向沿Z軸正向，大小為50 m/s。

表2 各工況碰撞區域Tab.2 Collision postions of each case

三種不同碰撞工況下碰撞力隨時間的變化曲線如圖15所示。由圖15可見，三條曲線差距不大，這是由于選取的三種不同碰撞位置處槳葉的厚度均較薄，碰撞位置對碰撞力的影響不大。但工況1、工況2和工況3的平均碰撞力分別為28.6 kN、27.2 kN和24.5 kN，即碰撞位置離葉根越遠，平均碰撞力呈現為略微增加的趨勢。

圖16所示為三種工況下槳葉單元最大應力時程曲線。圖17給出了0.6 ms時刻三種工況下的應力分布云圖，工況1的最大應力值最大。這是因為冰與槳葉碰撞的葉梢部位，其厚度和寬度均較小，使得葉梢區域受到撞擊時的剛度減少。工況1為典型工況，螺旋槳在高速旋轉時，葉梢部位受到冰塊撞擊的概率最大。此外，碰撞位置同樣處于葉緣，其離槳葉葉根越遠，槳葉的最大應力值就越大，對槳葉的損傷情況越嚴重。

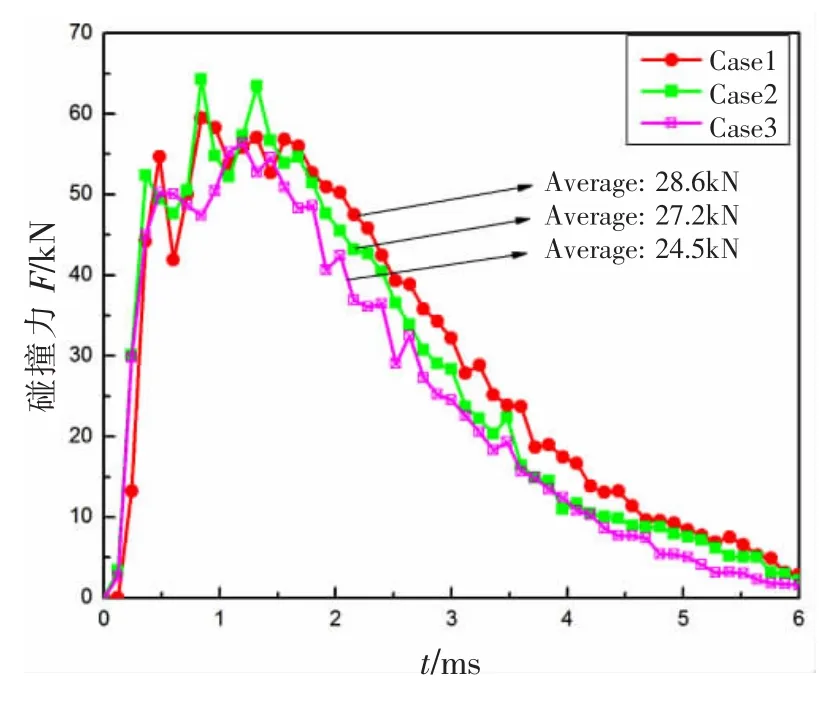
圖15 碰撞力—時間曲線Fig.15 Impact force-time curves

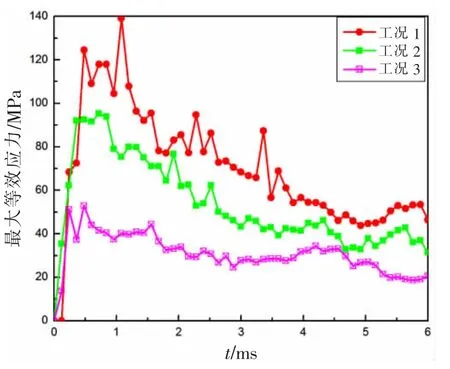
圖16 槳葉單元應力—時間曲線Fig.16 Blade elements maximum stress-time curves

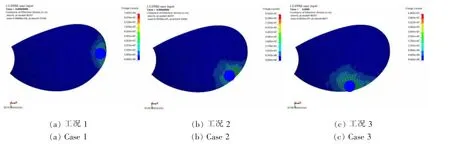
圖17 三種工況下槳葉應力分布云圖（t=0.6 ms）Fig.17 Blade stress contours of three cases(t=0.6 ms)

2.5 不同半徑冰與槳碰撞

碎冰塊呈現為無規則的形態，其形狀及尺寸千差萬別。數值模擬中，假定冰是球形，其半徑分別為0.05 m、0.10 m、0.15 m和0.20 m，碰撞位置如表2中的工況1，沖擊速度沿Z軸正向，大小為50 m/s。

不同半徑的冰球與槳碰撞時節點348的位移時程曲線和碰撞力時程曲線分別如圖18和圖19所示，可見，隨著冰的半徑的增大，相同時刻槳葉的變形也增大。同樣，冰的半徑越大，在碰撞過程中產生的碰撞力就越大。

圖20所示為不同半徑的冰球與槳碰撞下槳葉單元最大應力隨時間變化曲線，在相同條件下，冰的半徑越大，則對槳葉的損壞程度就越大。從圖20可以看出，冰的半徑r為0.20 m時，槳葉單元最大應力值將盡達到500 MPa，因此這樣的情況下對螺旋槳的損害是破壞性的。

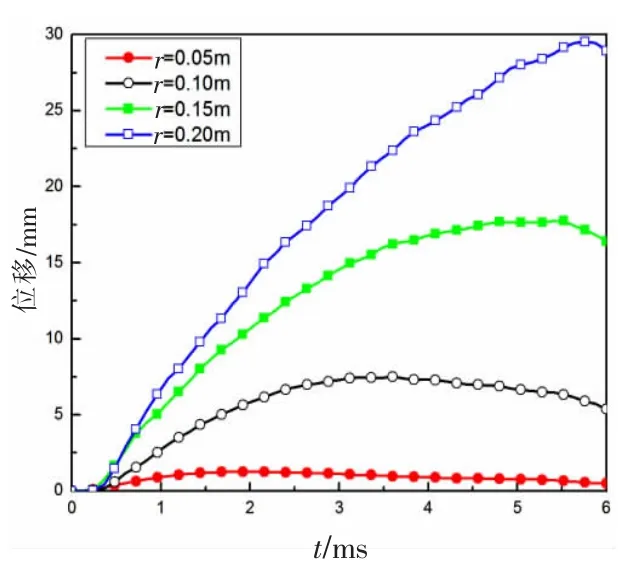
圖18 節點348位移—時間曲線Fig.18 Node 348 displacement-time curves

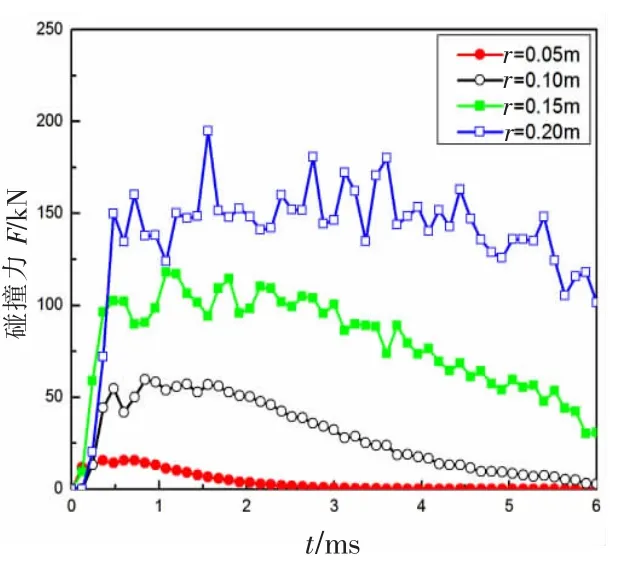
圖19 碰撞力—時間曲線Fig.19 Impact force-time curves

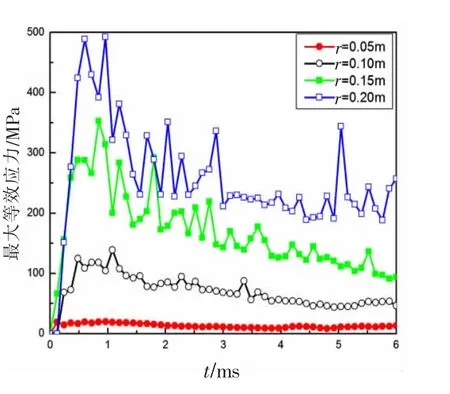
圖20 槳葉單元最大應力—時間曲線Fig.20 Elements maximum stress-time curves

3 結 論

本文對冰—槳碰撞問題進行了研究，針對螺旋槳與冰在不同速度、位置下碰撞和螺旋槳與不同半徑冰碰撞下的動態響應進行了數值模擬，得出結論如下：

（1）針對高速冰沖擊實例，冰模型采用SPH法，驗證了冰的數值模型及碰撞數值模擬計算方法的可行性。

（2）冰的沖擊速度越大，冰-槳碰撞越劇烈，槳葉的變形、單元最大應力和應變以及碰撞過程中產生的碰撞力均會越大，冰對槳葉造成的損傷情況越大。

（3）位于葉緣處的三種碰撞位置，其離槳葉葉根越遠，單元最大應力值就越大，對槳葉的損傷情況越嚴重。但選取的三種碰撞位置對碰撞力影響不大，碰撞位置離葉根越遠，平均碰撞力呈現為略微增加的趨勢。

（4）相同條件下，冰的半徑越大，即沖擊能量越大，槳葉的變形、單元最大應力以及碰撞過程中的碰撞力均越大，對槳葉的損傷情況越大。特別是冰的半徑為0.20 m時，槳葉單元最大應力值將盡達到500 MPa，在該工況下對螺旋槳的損害是破壞性的。

由于制約分析結果的因素復雜，本文忽略了流體環境及冰的形狀等參數的影響，數值模擬結果難免與實際出現偏差，但定性地得出了不同碰撞速度、位置和不同半徑冰對冰-槳碰撞問題的影響規律，可為今后的研究工作打下良好的基礎。

參 考 文獻：

[1]DNV.Ice strengthening of propulsion machinery[S].2011.

[2]ABS.Guidance notes on ice class[S].2005.

[3]IACS.URI3 machinery requirements for polar class ships[S].2006.

[4]胡志寬,桂洪斌,夏鵬鵬,等.冰載荷下船舶螺旋槳強度的有限元分析[J].船舶工程,2013,35(8)：12-15.Hu Zhikuan,Gui Hongbin,Xia Pengpeng,et al.Finite element analysis of ship propeller strength under ice loads[J].Ship Engineering,2013,35(8)：12-15.

[5]武文華,于佰杰,許 寧,等.海冰與錐體抗冰結構動力作用的數值模擬[J].工程力學,2008,25(11)：192-196.Wu Wenhua,Yü Baijie,Xü Ning,et al.Numerical simulation dynamic ice action on conical structure[J].Engineering Mechanics,2008,25(11)：192-196.

[6]Wang B,Yu H C,Basu R.Ship and ice collision modeling and strength evaluation of LNG ship structure[C].ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers,2008：911-918.

[7]劉 軍,李玉龍,劉元鏞.基于SPH方法的葉片鳥撞數值模擬研究[J].振動與沖擊,2008,27(9)：90-93.Liu jun,Li Yülong,Liu Yuanyong.Numerical simulation study of bird-impact on a blade using SPH method[J].Journal of Vibration and Shock,2008,27(9)：90-93.

[8]賈建東,李志強,楊建林,等.用SPH和有限元方法研究鳥撞飛機風擋問題[J].航空學報,2010,31(1)：136-142.Jia Jiandong,Li Zhiqiang,Yang Jianlin,et al.A study of bird impact on aircraft windshield using SPH and finite element method[J].Acta Aeronautica et Astronautica Sinica,2010,31(1)：136-142.

[9]Anghileri M,Castelletti L M L,Invernizzi F,et al.A survey of numerical models for hail impact analysis using explicit finite element codes[J].International Journal of Impact Engineering,2005,31(8)：929-944.

[10]Pernas-Sánchez J,Pedroche D A,Varas D,et al.Numerical modeling of ice behavior under high velocity impacts[J].International Journal of Solids and Structures,2012,49(14)：1919-1927.

[11]Carney K S,Benson D J,Du Bois P,et al.A high strain rate model with failure for ice in LS-DYNA[C].Proceedings of the Ninth International LS-DYNA Users Conference.2006：4-6.

[12]Carney K S,Benson D J,DuBois P,et al.A phenomenological high strain rate model with failure for ice[J].International Journal of Solids and Structures,2006,43(25)：7820-7839.

[13]Keegan M H,Nash D,Stack M.Numerical modelling of hailstone impact on the leading edge of a wind turbine blade[J].EWEA Annual Wind Energy Event 2013,2013.

[14]Hu Zhikuan,Gui Hongbin,Xia Pengpeng,et al.Dynamic response analysis of the collision between ice and propeller at high speed[C].The Society for Underwater Technology Conference(SUTTC 2013),2013：72-76.