滑動軸承—行星齒輪耦合系統非線性動力學特性研究

李同杰，靳廣虎，鮑和云，朱如鵬

（1.南京航空航天大學 機電學院，南京 210016；2.安徽科技學院 機械工程學院，安徽 滁州 233100）

0 引 言

行星齒輪傳動具有承載能力強、功重比大、體積小等優點，被廣泛應用到船舶、汽車、航空、起重機械等領域。由于其動特性的優劣直接影響著機器運行品質的高低，所以行星齒輪傳動系統動力學特性的研究吸引了大批專家學者的關注目光[1-6]。在有大功率傳遞需要的場合（比如船舶、航空）行星齒輪傳動系統經常采用滑動軸承支撐，所以將滑動軸承與行星齒輪傳動集于一個系統內，開展滑動軸承—行星齒輪耦合系統的動力學特性研究就具有重要的工程價值。

國內外學者早已證實了滑動軸承對其轉子的支撐力呈現出強非線性特質，并獲得了其非線性解析表達式[7-9]。另外，行星齒輪傳動中齒側間隙的存在也會產生分段非線性[2]。所以滑動軸承-行星齒輪耦合系統動力學模型的本質是一個非光滑強非線性系統。目前，關于行星齒輪系統動力學的研究通常是把各構件的支撐軸承假定為一個定常彈簧，把軸承對各構件的支撐力假設為一個隨其位移線性變化的一次函數來處理[10-13]，慮及滑動軸承非線性力作用的行星輪系動特性的研究尚非常少見。周志剛[14]研究了非線性滾動軸承力作用下的風力發電機行星齒輪傳動系統在變載荷作用下所表現出來的動特性。卜忠紅[15]在考慮了滑動軸承的剛度不對稱性的基礎上，研究了行星輪在滑動軸承支撐下的人字齒輪行星傳動的固有特性，但其軸承力依然采用的是線性模型。

本文將在充分考慮滑動軸承非線性油膜力以及齒側間隙等固有非線性因素的基礎上，建立滑動軸承—行星齒輪傳動系統的動力學模型，并對其耦合非線性動力學特性進行初步研究。

1 滑動軸承—行星齒輪耦合動力學模型

圖1是滑動軸承支撐下2K-H型行星齒輪傳動的運動簡圖。其中太陽輪、行星架均被滑動軸承支撐，TD是功率輸入端扭矩，TL是功率輸出端扭矩，字母z表示齒數，其角標s、pi、r分別指代太陽輪、第i個行星輪以及內齒圈（下文角標指示規則亦同）。

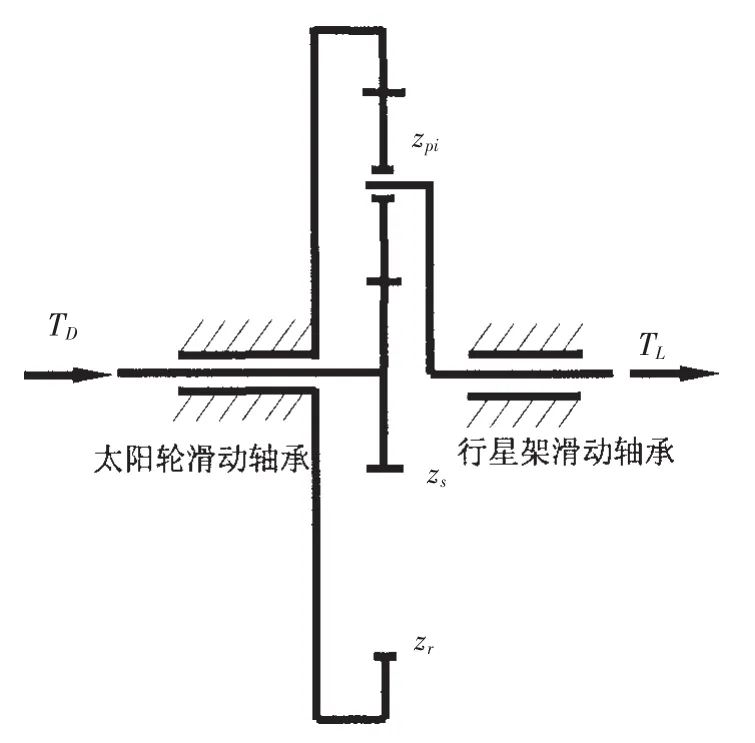
圖1 行星齒輪系統傳動簡圖Fig.1 Kinematic sketch of planetary gear train

圖2 滑動軸承非線性油膜力模型Fig.2 Nonlinear oil film force of slide bearing

1.1 滑動軸承非線性油膜力

圖2是滑動軸承作用在轉子上的非線性油膜力模型。半徑為r的轉子中心在O1點，半徑為R的軸承中心在O點。由于潤滑油的粘性，轉子以角速度ω轉動時必然會帶動潤滑油進入到轉子與軸承間的楔形空間，從而形成一定的油膜壓力F（其水平和豎直分力分別以Fx和Fy來表示）支撐起轉子來達到一種動態平衡。國內外專家學者的研究發現，作用在轉子上的油膜力除了與軸承長度L、軸承半徑間隙C、潤滑油粘度μ、軸承半徑R等系統參數有關外，還與轉子徑向位移以及速度成復雜的非線性關系[7-9]，其量綱歸一化后的非線性表達式 fx和 fy表述如（1）、（2）式所示。

上式中，x、y表示轉子在水平以及豎直方向上的徑向位移，x˙及y˙分別表示轉子徑向速度在x、y方向上投影，M為轉子的軸端集中質量。

1.2 滑動軸承—行星齒輪耦合系統的非線性動力學模型

圖3是滑動軸承-行星齒輪耦合系統的非線性動力學模型。模型中的行星齒輪傳動部分采用經典的彎扭耦合振動模型[3]，在此簡單介紹如下：分別建立一個固定于基礎之上的定參考系x-O-y和一個固定于行星架上的動參考系H-O-V。內齒圈固定于基礎之上，無任何轉動與徑向位移；太陽輪受滑動軸承支撐，考慮其中心橫向位移（動參考系下表達為Hs，Vs）以及一個轉動角位移θs；行星架也受滑動軸承支撐，考慮其中心橫向位移（動參考系下表達為Hc，Vc）以及一個轉動角位移θc；行星輪均假設為剛性支撐，只考慮每個行星輪的轉動角位移θpi。這樣系統在動參考系下的自由度就包括行星架（Hc,Vc,θc），太陽輪（Hs,Vs,θs），行星輪 θpi（i=1,2,…， N），系統共有（6+N）個自由度，其廣義坐標X可表示為

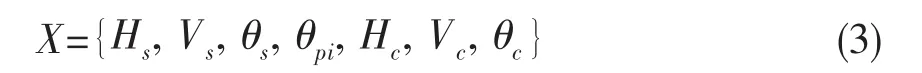
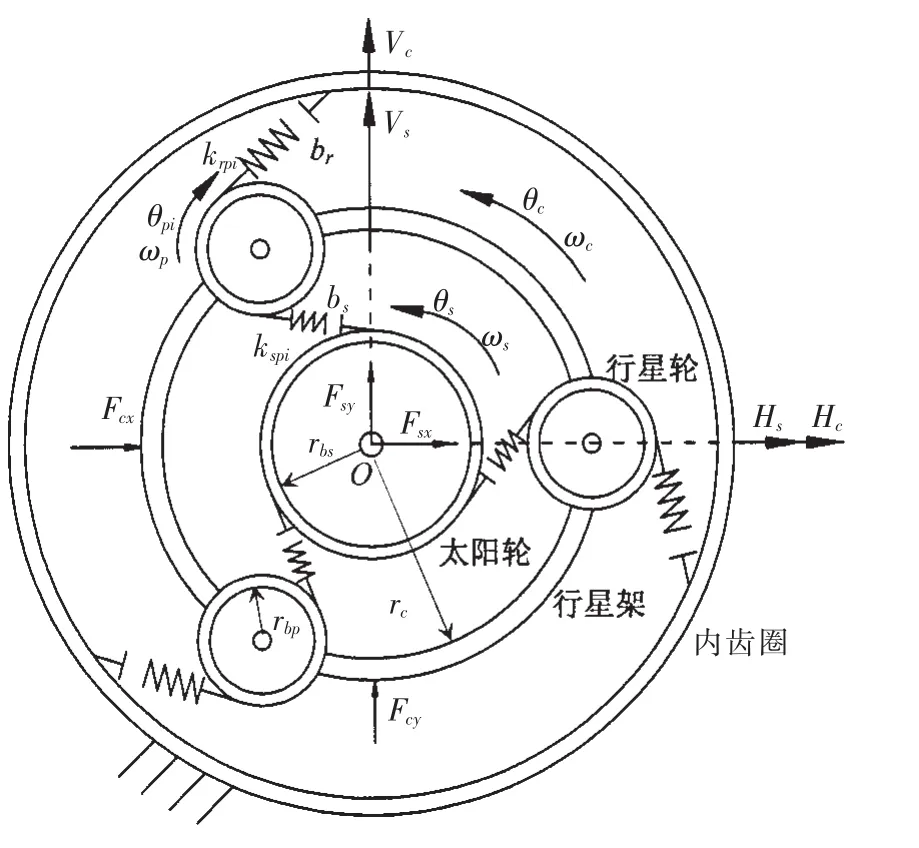
圖3 滑動軸承—行星齒輪耦合系統的非線性動力學模型Fig.3 Nonlinear dynamical model of slide bearingplanetary gear train system

圖3中，Fsx、Fsy分別表示太陽輪滑動軸承油膜力在定參考系下的水平與鉛直方向投影；Fcx、Fcy分別表示行星架轉子的滑動軸承油膜力在定參考系下的水平與鉛直方向投影；kspi表示太陽輪和第i路行星輪之間的嚙合剛度；krpi表示行星輪和和第i路行星輪之間的嚙合剛度。上述嚙合剛度大致隨時間呈矩形波變化；bs為太陽輪和行星輪之間的半齒側間隙；br為行星輪和內齒圈之間的半齒側間隙。ωj（j=s,c,pi）表示相應活動構件的角速度；rbs、rbp分別為太陽輪、行星輪的基圓半徑；rc為行星架半徑。

注意到非線性油膜力表達式（1）、（2）是在定參考系x-O-y下建立的，所以應把太陽輪以及行星架在動坐標系H-O-V下的徑向位移與速度轉化定坐標系x-O-y下的對應量。以xs、ys、xc和yc分別表示太陽輪以及行星輪在定參考系的徑向位移，x˙s、y˙s、x˙c和y˙c分別表示太陽輪以及行星輪在定參考系的徑向位移，代入（1）、（2）式就能夠獲得各滑動軸承的非線性油膜力表達式，具體為

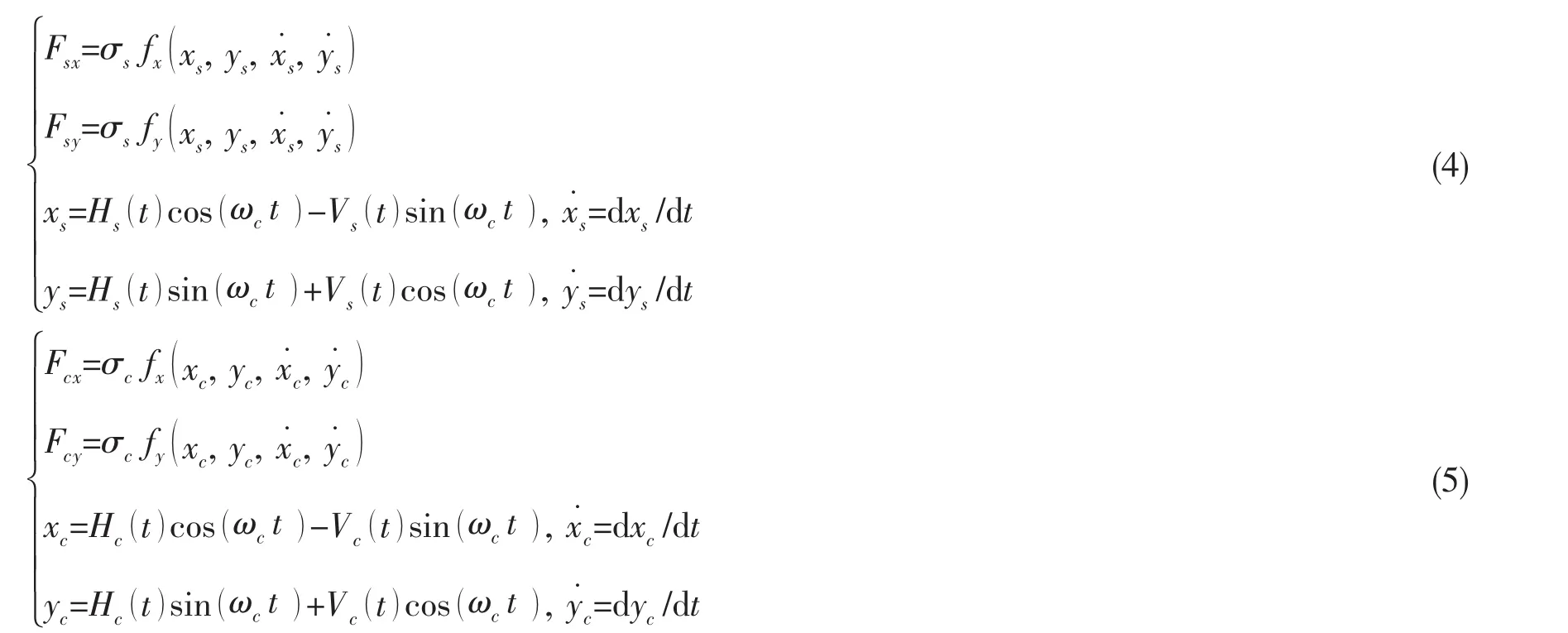
式中：σs、σc分別為太陽輪、行星架滑動軸承參數所決定的Sommerfeld系數。

系統各內、外齒輪副動態嚙合力Pspi、Prpi表達式分別為相應內外嚙合副嚙合點相對位移Yspi、Yrpi的函數

式中：按矩形波時變的嚙合剛度kspi（t ）、krpi（t）可以展開成為以嚙合頻率為基頻的傅里葉級數，反映齒側間隙所帶來的分段非線性的間隙非線性函數f表達式為

式中：Y為系統某一路齒輪副的嚙合點相對位移，可取Yspi或Yrpi；b為該路齒輪副的半齒側間隙，根據齒輪副的內外而取br或bs。

1.3 系統的運動微分方程

由剛體平面運動微分方程以及剛體定軸轉動微分方程，容易寫出圖3所示滑動軸承—行星齒輪非線性耦合系統的運動微分方程如下式所示：

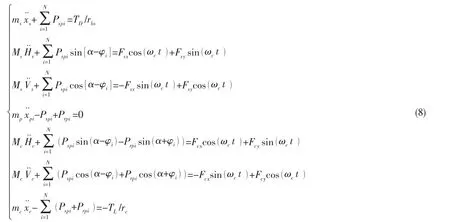
式中：Ms和Mc分別為太陽輪以及行星架質量；ms、mc和mp分別為太陽輪、行星架和行星輪的當量質量；α為齒輪壓力角；rbc為行星架當量基圓半徑；φi為第i個行星輪相當于第一個行星輪的位置角。本節中所涉及參數的具體表達式在文獻[2]、[3]中已有詳細說明，在此不再贅述。

2 滑動軸承—行星齒輪耦合非線性系統動特性的數值仿真

采用直接數值積分的方法求解方程（8），可以仿真獲得滑動軸承—行星齒輪耦合系統的動特性。仿真案例參數如下：模數 m=2.5，齒數 zs=20，zpi=40，zr=110，齒輪壓力角 α=20°，質量 Ms=0.386 kg，Mc=1.824 kg，當量質量 ms=0.246 kg、mc=1.153 kg、mpi=0.690 kg，行星輪個數 N=3，太陽輪軸（軸承）直徑 ds=35 mm，行星架軸（軸承）直徑dr=52 mm，齒側間隙bs=20 um，br=20 um，根據減速器滑動軸承參數的工程取值范圍[16]，軸承相對間隙取ψ=[0.2‰～1.5‰]，軸承寬徑比L/d=1。

2.1 非線性滑動軸承力對行星齒輪動系動特性的影響

取軸承相對間隙ψ=1‰，太陽輪轉速ωs=200 rad/s，研究非線性滑動軸承力對行星齒輪系動特性的影響規律。為了便于對比參照，本文首先仿真了線性彈簧支撐假設下的行星齒輪傳動系統的太陽輪軸心軌跡、太陽輪軸承支撐力、以及各外嚙合副的動態嚙合力，分別如圖4～6所示。由于行星架的軸心軌跡圖與太陽輪軸心軌跡圖形態類似，內嚙合副的動態嚙合力與外嚙合副變化規律類似，本文不再另外給出系統行星架的軸心軌跡圖以及各內嚙合副的動態嚙合力曲線。

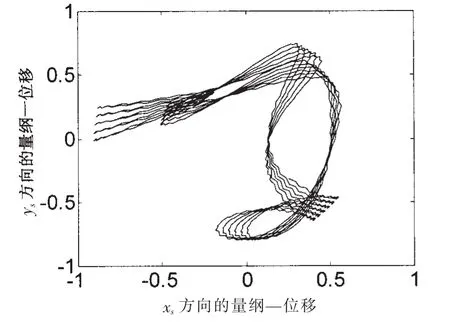
圖4 線性彈簧支撐下的太陽輪軸心軌跡Fig.4 Axis trace of sun gear supported by linear spring

圖5 線性彈簧支撐下的太陽輪軸承力Fig.5 Bearing force of the sun gear

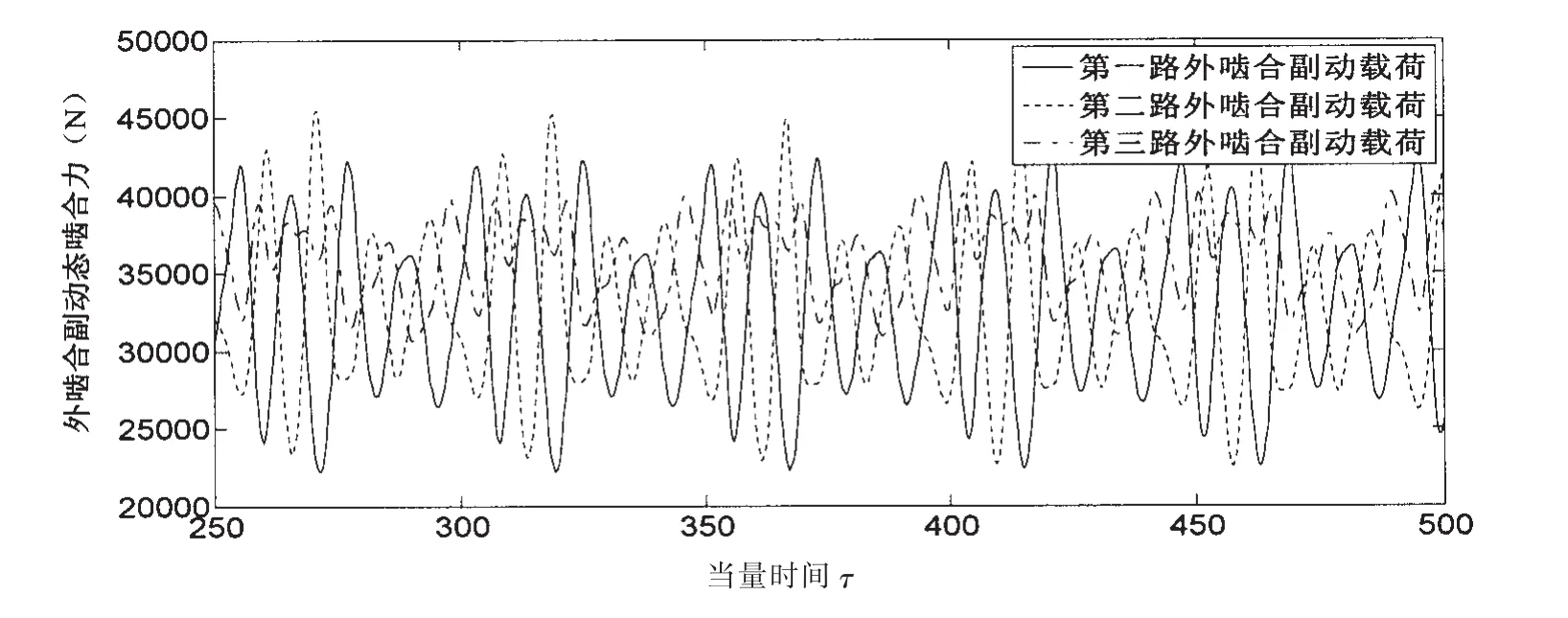
圖6 線性彈簧支撐下的外嚙合副動態嚙合力Fig.6 External gear pair dynamic load of the system supported by linear spring

圖4（橫縱坐標中的量綱—位移為位移與軸承間隙的比值，下同）所顯示的太陽輪軸心軌跡是一條轉折點眾多的扭曲封閉曲線，軌跡中大量的彎折點反映了各齒輪副矩形波時變嚙合剛度所導致的嚙頻激振力對軌跡的影響，整體封閉的曲線則說明系統的運動處于周期狀態；圖5（橫坐標當量時間為時間與行星輪系固有頻率的乘積，下同）顯示系統軸承力波動出現了線性振動系統所特有的 “拍振現象”，反映出了線性彈簧支撐假設的影響；圖6顯示系統各路外嚙合副的動態嚙合力隨時間的變化規律均呈現出某種長周期運動狀態，變化非常規則。

圖7～9分別是滑動軸承非線性油膜力作用下行星齒輪傳動系統的太陽輪軸心軌跡、太陽輪軸承支撐力、以及各外嚙合副的動態嚙合力。可以看到，圖7中的太陽輪軸心軌跡變得雜亂無章，但是明顯比圖4中的軌跡要光滑許多，僅在局部出現了輕微的折線波動，顯示了滑動軸承油膜對系統嚙頻激振響應的鎮靜作用。圖8所示的軸承力時域曲線中“拍振現象”已經消失，取而代之的是毫無運動規律可言的混沌運動。圖9所示動態嚙合力的變化規律進一步復雜化，已經沒有了圖6所示的長周期運動的特征，顯示了軸承非線性油膜力對齒輪副動態嚙合力的影響。

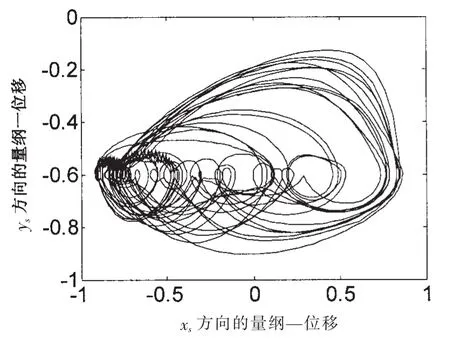
圖7 非線性油膜力作用下的軸心軌跡Fig.7 Axis trace of sun gear supported by nonlinear oil film force

圖8 太陽輪軸承非線性油膜力振蕩曲線Fig.8 The oscillation curve of slide bearing nonlinear oil film force

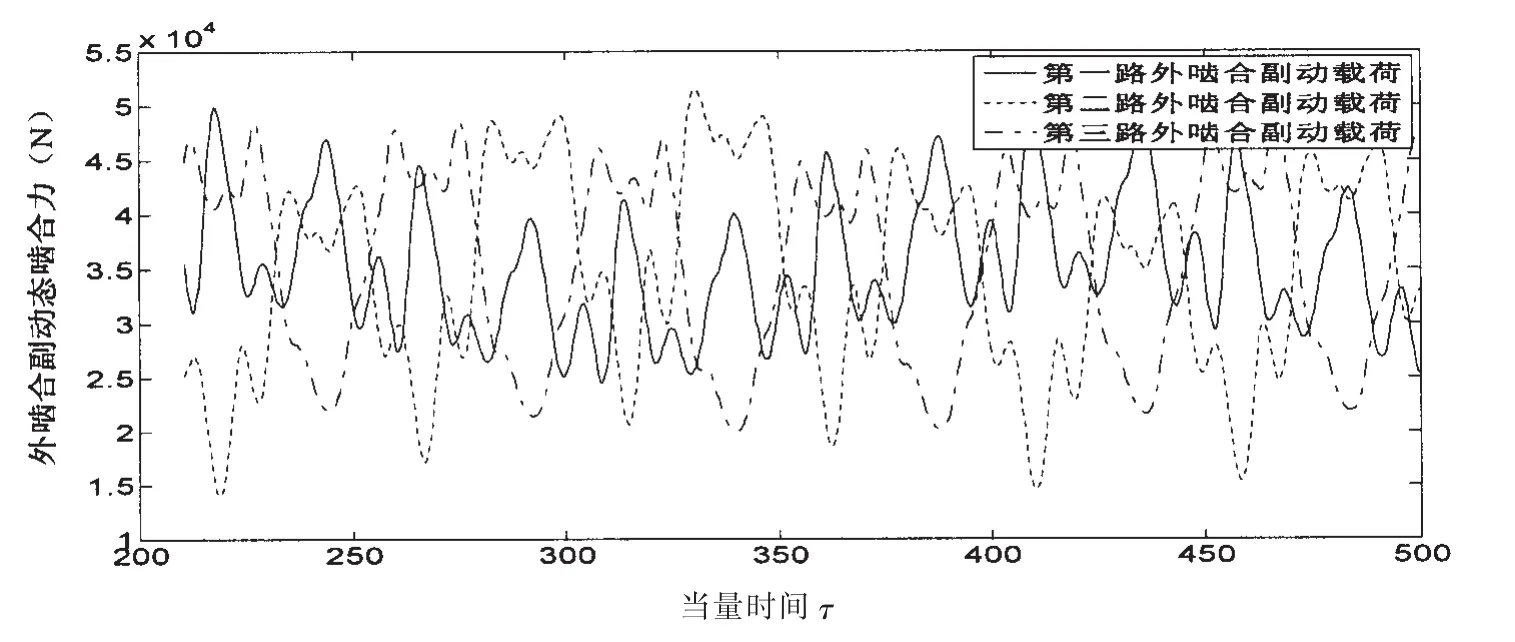
圖9 非線性油膜力作用下的系統外嚙合副動態嚙合力Fig.9 External gear pair dynamic load of the system supported by nonlincear oil film force

總結上述仿真結果，可以獲得如下結論：滑動軸承的非線性油膜力對行星齒輪傳動系統的動特性影響非常顯著并且復雜。一方面滑動軸承的油膜會使行星輪系對各活動構件的嚙頻振蕩起到鎮定作用，另一方面卻可能導致系統軸承力波動呈現混沌狀態，使各齒輪副動態嚙合力的波動失去周期規律。所以，把滑動軸承以及行星齒輪傳動集于一個系統內，研究二者之間的耦合動力學特性就顯得非常必要了。

2.2 轉速對耦合系統動特性的影響

為了探究轉速對滑動軸承—行星齒輪耦合系統動特性的影響規律，在保持其他系統參數不變的條件下，將太陽輪軸轉速增大為ωs=500 rad/s，計算太陽輪軸承非線性油膜力振蕩曲線以及太陽輪軸心軌跡分別如圖10、圖11所示。

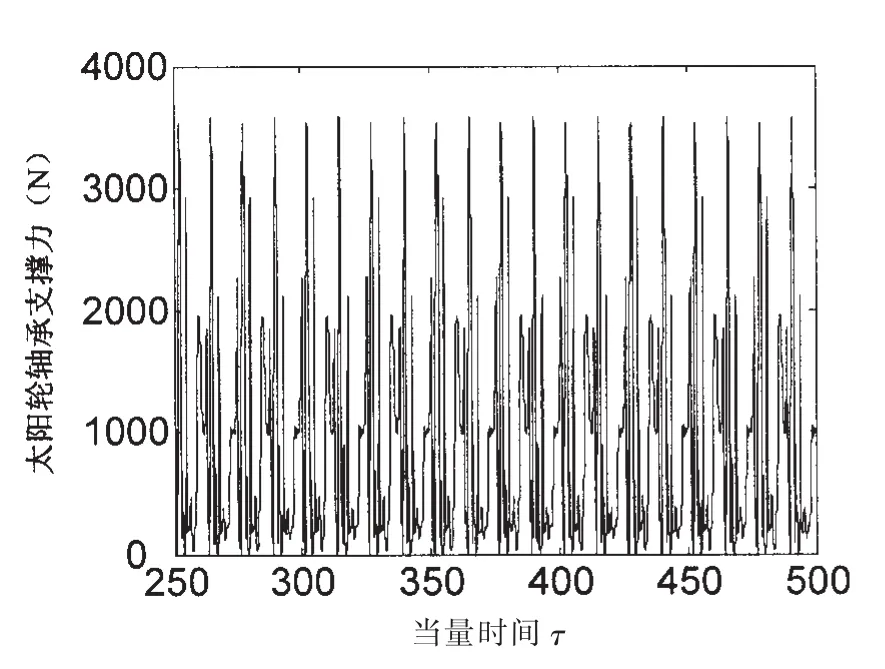
圖10 ωs=500 rad/s時軸承油膜力振蕩曲線Fig.10 Nonlinear oil film force when ωs=500 rad/s

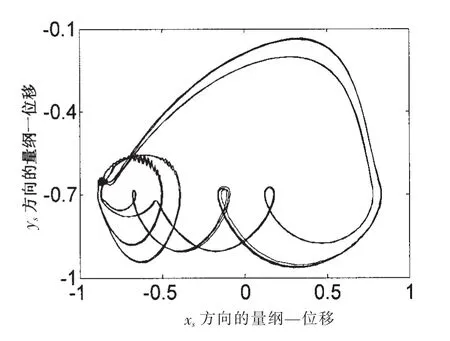
圖11 ωs=500 rad/s時太陽輪軸心軌跡Fig.11 Axis trace of sun gear when ωs=500 rad/s

將太陽輪軸轉速進一步增大為ωs=1 000 rad/s，再次計算太陽輪軸承非線性油膜力時域曲線以及太陽輪軸心軌跡分別如圖12、圖13所示。

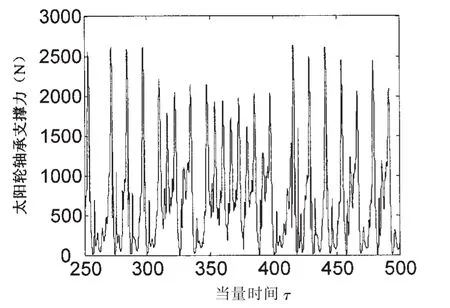
圖12 ωs=1 000 rad/s時軸承油膜力振蕩曲線Fig.12 Nonlinear oil film force when ωs=1 000 rad/s

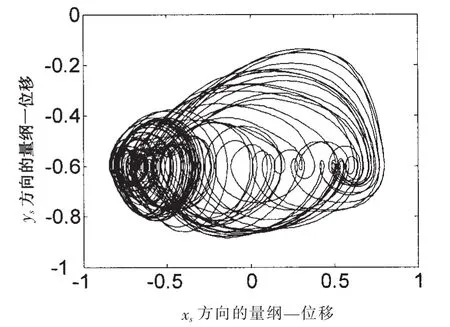
圖13 ωs=1 000 rad/s時太陽輪軸心軌跡Fig.13 Axis trace of sun gear when ωs=1 000 rad/s

圖10顯示，當轉速增大到ωs=500 rad/s時系統太陽輪軸承力由低速時（ωs=200 rad/s）的混沌運動（圖8）進入到了某種周期運動，進一步增大轉速到ωs=1 000 rad/s，系統軸承力的振動再次進入到非周期運動狀態（圖12）。說明太陽輪轉速會對系統軸承力的振動規律產生本質影響，轉速的變化能夠導致軸承力運動形態在周期運動和混沌之間分岔。

圖11顯示，當轉速增大到ωs=500 rad/s時太陽輪軸心浮動軌跡中的折線波動現象得到弱化（對比轉速為ωs=200 rad/s時的軌跡圖7），進一步增大轉速到ωs=1 000 rad/s，太陽輪軸心軌跡中的折線波動現象完全消失，軌跡變得完全光滑（圖13所示）。說明隨著轉速的上升，非線性軸承油膜力在影響系統運動的激振力中逐漸占據了主導地位，而嚙頻激振力對系統的影響逐漸弱化直至消失。

2.3 軸承間隙對行星輪系各齒輪副嚙合特性的影響

作為減速器用的滑動軸承相對間隙ψ=C/R的取值范圍通常在0.2‰～1.5‰之間[16]，而本文仿真案例中的太陽輪軸半徑為17.5 mm，那么其滑動軸承間隙工程可取范圍為0.35×10-5m～2.6×10-5m之間。為了研究滑動軸承間隙對行星齒輪傳動系統齒輪副嚙合特性的影響規律，以下固定其他系統參數不變，在太陽輪軸承間隙的可取范圍0.35×10-5m～2.6×10-5m內取三個不同間隙值C=0.5×10-5m、C=1×10-5m、C=2×10-5m，仿真系統的各外嚙合副動載荷時變曲線分別如圖14～16所示。

圖14顯示在C=0.5×10-5的軸承間隙下，系統各外嚙合副均處于正常嚙合狀態，且各路動載荷呈現出明顯的周期規律性；圖15顯示當間隙增大到C=1×10-5m時，系統外嚙合已經出現了單邊沖擊現象，即有些齒輪副出現了正常嚙合到空嚙合（某些齒輪副嚙合力出現短暫零值）的循環沖擊狀態；圖16顯示當間隙增大到C=2×10-5時，系統外嚙合副再次進入到正常嚙合狀態，但與圖14所示的正常嚙合狀態相比，動載荷的振動幅值有了明顯降低，且波動形態也有了顯著變化。

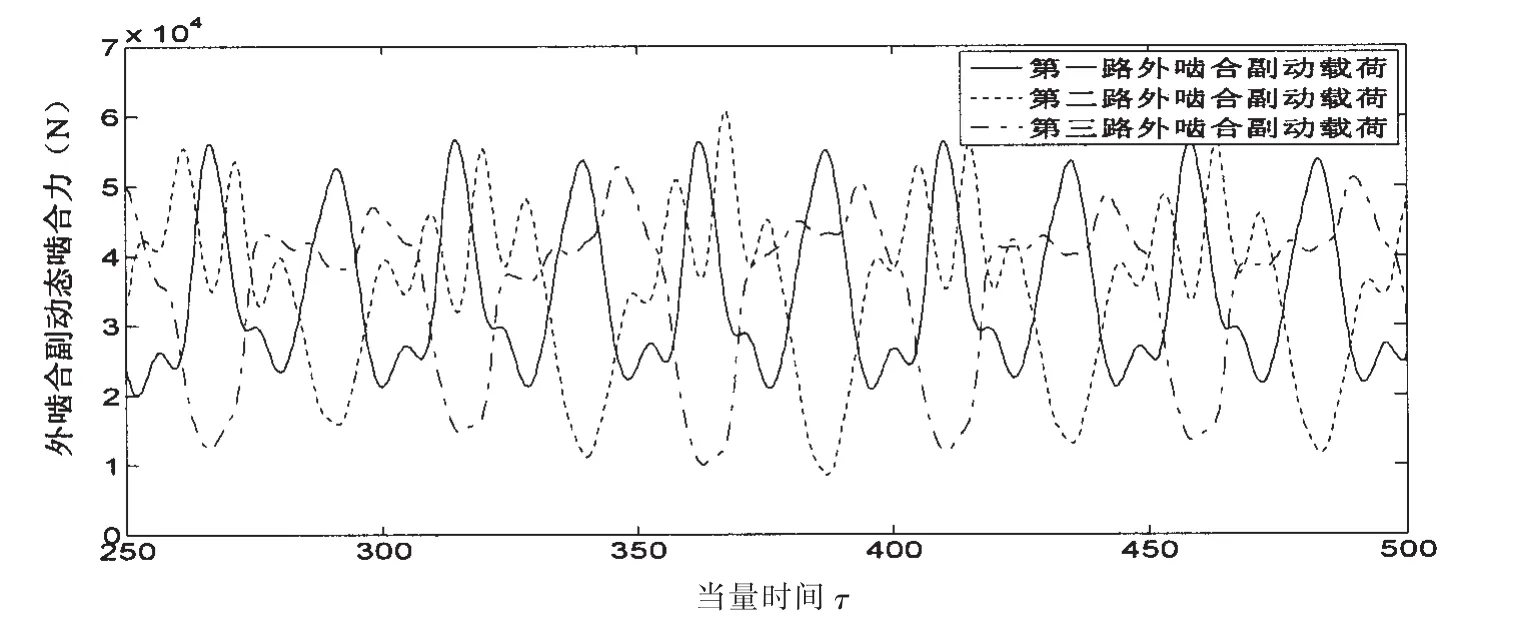
圖14 C=0.5×10-5時耦合系統的外嚙合副動載荷Fig.14 External gear pair dynamic load of the system when C=0.5×10-5

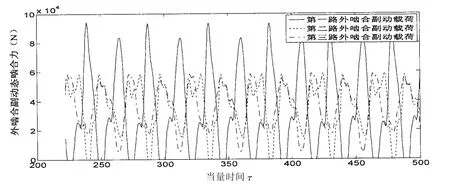
圖15 C=1×10-5m時耦合系統外嚙合副動載荷Fig.15 External gear pair dynamic load of the system when C=1×10-5m

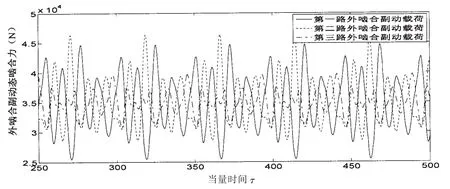
圖16 C=2×10-5時耦合系統外嚙合副動載荷Fig.16 External gear pair dynamic load of the system when C=2×10-5m

總結上述仿真結果可以確定，滑動軸承間隙值非常顯著地影響著行星齒輪傳動系統各齒輪副的嚙合特性，間隙的的取值不當可能導致單邊沖擊狀態的出現，嚴重影響著行星齒輪傳動系統的運行品質。從仿真結果來看，系統齒輪副的嚙合狀態（正常與否）隨軸承間隙的變化并非是一種單調的線性規律。在工程可取的間隙區間內經過大量的采樣取值，重復進行數值仿真試驗可以獲得滑動軸承-行星齒輪耦合非線性系統的齒輪副嚙合狀態隨軸承間隙值的具體變化規律，如圖17所示。

圖17中，橫坐標表示太陽輪滑動軸承間隙值，縱坐標表示相應軸承間隙下系統所有各路外齒輪副中動載荷波動的最小值。這樣，縱坐標取正值則說明齒輪副正常嚙合，取零值則反映某些齒輪副的嚙合狀態出現了單邊沖擊現象。圖17的變化趨勢說明，在工程可取的軸承間隙范圍內，存在兩個導致行星齒輪傳動系齒輪副發生單邊沖擊現象的軸承間隙小區間，分別介于7.05×10-6m～8.24×10-6m 以及 1.29×10-5m～1.42×10-5m 之間。所以，軸承間隙值對系統齒輪副嚙合狀態的影響是一個非常復雜的非線性規律，機械工程師需要謹慎選擇其取值，以避免單邊沖擊現象的出現。

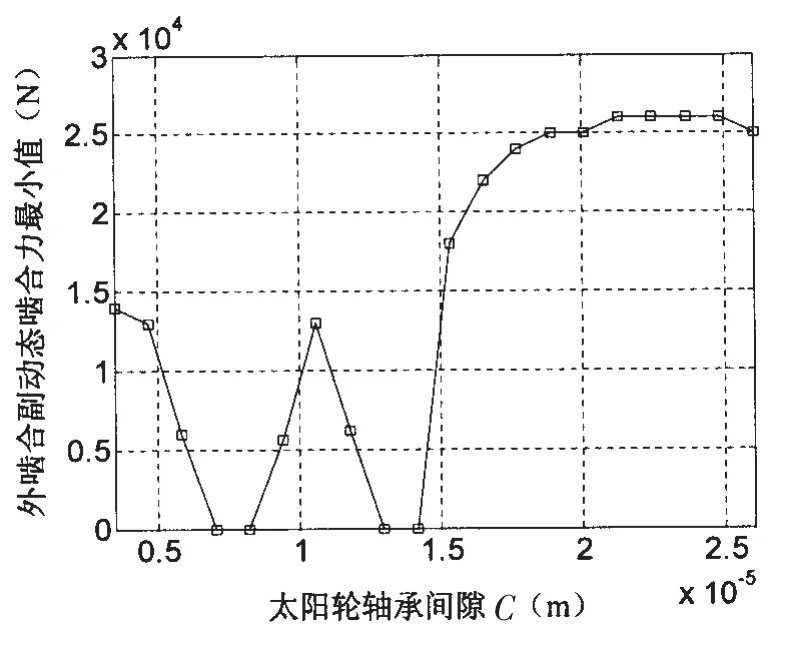
圖17 系統嚙合狀態隨滑動軸承間隙值的變化曲線Fig.17 The oscillation curve of meshing state with slide bearing clearance

3 結 論

（1）本文建立了滑動軸承-行星齒輪耦合系統的非線性動力學模型，模型中充分考慮了滑動軸承的非線性油膜力以及行星齒輪齒側間隙等非線性因素。

（2）滑動軸承的非線性油膜力對行星齒輪傳動系統的動特性影響非常顯著并且復雜。一方面滑動軸承的油膜會對行星齒輪系中各活動構件的嚙頻振動起到鎮定作用，另一方面也可能導致系統軸承力波動呈現混沌狀態，使各齒輪副動態嚙合力的振動失去周期規律。

（3）行星輪系輸入軸轉速對系統軸承力的振動規律會產生本質影響，轉速的變化能夠導致軸承力振動形態在周期運動和混沌之間分岔。

（4）滑動軸承間隙值非常顯著地影響著行星齒輪傳動系統齒輪副的嚙合特性，并且影響規律是一個非常復雜的非線性映射關系，間隙取值不當可能導致單邊沖擊現象的出現。

參 考 文 獻：

[1]李瑰賢,趙永強,常 山,等.船用兩級雙排斜齒行星齒輪系統動力學方程的建立[J].船舶力學,2011,15(5)：530-537.Li G X,Zhao Y Q,Chang S,et al.Study on dynamic governing equations of two stage double helical tooth planetary gear train used in ship[J].Journal of Ship Mechanics,2011,15(5)：530-537.(in Chinese)

[2]李同杰,朱如鵬,鮑和云,等.行星齒輪系扭轉非線性振動建模與運動分岔特性研究[J].機械工程學報,2011,47(21)：76-83.Li T J,Zhu R P,Bao H Y.Nonlinear torsional vibration modeling and bifurcation characteristic study of a planetary gear train[J].Journal of Mechanical Engineering,2011,47(21)：76-83.(in Chinese)

[3]Sun T,Hu H Y.Nonlinear dynamics of a planetary gear system with multiple clearances[J].Mechanism and Machine Theory,2003,38：1371-1390.

[4]Ambarisha V K,Parker R G.Nonlinear dynamics of planetary gears using analytical and finite element models[J].Journal of Sound and Vibration,2007,302：577-595.

[5]Chen Z G,Shao Y M.Dynamic simulation of planetary gear with tooth root crack in ring gear[J].Engineering Failure Analysis,2013,31：8-18.

[6]Guo Y,Parker R G.Dynamic analysis of planetary gears with bearing clearance[J].Journal of Computational and Nonlinear Dynamics,2012,7：041002-1-15.

[7]Adiletta G,Guido A R,Rossi C．Nonlinear dynamics of a rigid unbalanced rotor in journal bearings.part I：Theoretical analysis[J].Nonlinear Dynamics,1997,14(2)：57-87．

[8]Adiletta G,Guido A R,Rossi C.Nonlinear dynamics of a rigid unbalanced rotor in journal bearings.part II：Experimental analysis[J].Nonlinear Dynamics,1997,14(2)：157-189．

[9]Zhang W.Modeling of nonlinear oil-film force acting on a journal with unsteady motion and nonlinear instability analysis under the model[J].International Journal of Nonlinear Sciences and Numerical Simulation,2000,1(3)：179.

[10]王世宇,宋軼民,沈兆光,等.行星傳動系統的固有特性及模態躍遷研究[J].振動工程學報,2005,18(4)：412-417.Wang S Y,Song Y M,Shen Z G.Research on natural characteristics and loci veering of planetary gear transmissions[J].Journal of Vibration Engineering,2005,18(4)：412-417.(in Chinese)

[11]劉振皓,巫世晶,王曉筍,等.基于增量諧波平衡法的復合行星齒輪傳動系統非線性動力學[J].振動與沖擊,2012,31(3)：117-122.Liu Z H,Wu S J,Wang X S.Nonlinear dynamics of compound planetary gear sets based on incremental harmonic balance method[J].Journal of Vibration and Shock,2012,31(3)：117-122.(in Chinese)

[12]Singh A.Application of a system level model to study the planetary load sharing behavior[J].ASME,Journal of Mechanical Design,2005,127(12)：469-476.

[13]Ambarisha V K,Parker R G.Nonlinear dynamics of planetary gears using analytical and finite element models[J].Journal of Sound and Vibration,2007,302：577-595.

[14]周志剛,秦大同,楊 軍,等.變載荷下風力發電機行星齒輪傳動系統齒輪—軸承耦合動力學特性[J].重慶大學學報,2012,35(12)： 7-14.Zhou Z G,Qin D T,Yang J,et al.Gear-bearing coupling dynamics characteristics of wind turbine planetary gear transmission system under variable load[J].Journal of Chongqing University,2012,35(12)：7-14.(in Chinese)

[15]卜忠紅,劉 更,吳立言.滑動軸承支承人字齒輪行星傳動固有特性分析[J].機械工程學報,2011,47(1)：80-88.Bu Z H,Liu G,Wu L Y.Natural characteristics analysis on herringbone planetary gear trains with slide bearing support[J].Journal of Mechanical Engineering,2011,47(1)：80-88.(in Chinese)

[16]成大先.機械設計手冊（第5版）[M].北京：化學工業出版社,2008.Cheng D X.Handbook of mechanical design(the fifth edition)[M].Beijing：Chemical Industry Publishing House,2008.(in Chinese)