端面轉角對板架結構極限強度的影響研究

張亦龍，岳亞霖，韋朋余，曾慶波，張 濤，陳 哲

（中國船舶科學研究中心，江蘇 無錫 214082）

0 引 言

主甲板板架是船舶的主要承力部件，在船體中承擔巨大的載荷，若其強度不足會導致船舶結構達不到設計承載指標而提前崩潰，因此主甲板板架結構的極限強度驗證是船舶設計工作中的重點。有關船舶板架結構的研究成果很多，如吳衛國等[1]采用非線性有限元法研究了影響船體大開口甲板板架穩定性的主要因素；孔令濱等[2]對比了不同載荷和形狀尺寸下大開口式玻璃鋼夾層板架結構力學性能的差異；朱漢波等[3]提出了一種修正船舶設計規范中Smith法扶強材單元載荷-端縮曲線的方法來解決船體多跨板架結構整體失穩的問題；Wang等[4]研究了完整和帶裂紋的加筋板剪切極限強度，對初始撓度和柔度等進行了參數分析并給出了經驗公式；張錦嵐等[5]研究了補強方式和貼板厚度等對局部腐蝕加筋板補強后強度的影響；Shanmugam等[6]對板架結構在面內和側向壓力聯合作用下的響應開展了試驗研究，結果表明板架承受側向載荷的能力隨著軸向載荷的增加而降低；祁恩榮等[7]根據彈性大撓度理論和剛塑性分析得到了加筋板格高級屈曲分析方法，并開發了相關分析軟件。

板架模型試驗法是研究船體主甲板板架極限強度的重要方法之一。艙段結構在中拱或中垂狀態下，由于甲板板架整體受拉或受壓，通常在板架結構極限強度試驗中僅考慮板架端部的簡單拉伸或壓縮，實現縱向位移加載[8]；但是艙段橫截面繞中和軸旋轉，產生彎曲變形，因此艙段中主甲板板架的變形可以分為兩個方面：縱向拉伸或壓縮、橫截面旋轉，如果在試驗中不考慮板架端部橫截面的旋轉對板架極限強度的影響，有可能導致試驗給出的板架結構極限強度和失效模式與實船中的甲板板架部分不同，無法對實船甲板板架的極限強度進行正確的分析與評估。中垂狀態下，艙段結構主甲板受壓，存在穩定性問題，其極限強度通常比中拱狀態下小，因此有必要研究端面轉角對甲板板架受壓狀態下極限強度的影響。

本文采用非線性有限元法，以單層甲板板架、開孔單層甲板板架和雙層甲板板架為研究對象，對比分析板架受壓時，不同的端面轉角下板架的極限載荷和失效模式，研究了端面轉角對板架極限強度的影響規律。

1 端面轉角對單層板架受壓極限強度的影響研究

本文設計了單層甲板板架模型，選取不同的端面轉角，利用準靜態分析法進行極限強度分析，對比研究了不同端面轉角下單層板架的極限載荷和失效模式。

1.1 單層板架模型設計

單層板架模型取自某箱型三艙段結構主甲板板架，縱向長度為3 900 mm，每個艙段的板架長1 300 mm,橫截面寬度為2 100 mm；甲板上設有9根“T”型材作為縱桁，12根扁鋼作為縱骨，相鄰兩縱向構件間距100 mm；每隔200 mm設有與縱桁橫截面尺寸相同的橫梁；板架舷側部位保留高度為335mm的原艙段舷側結構，沿縱向焊接翼板形成加強筋。材料為理想彈塑性，彈性模量為210 MPa，泊松比為0.28，屈服極限為235 MPa。模型結構型式如圖1所示，橫截面屬性見表1。

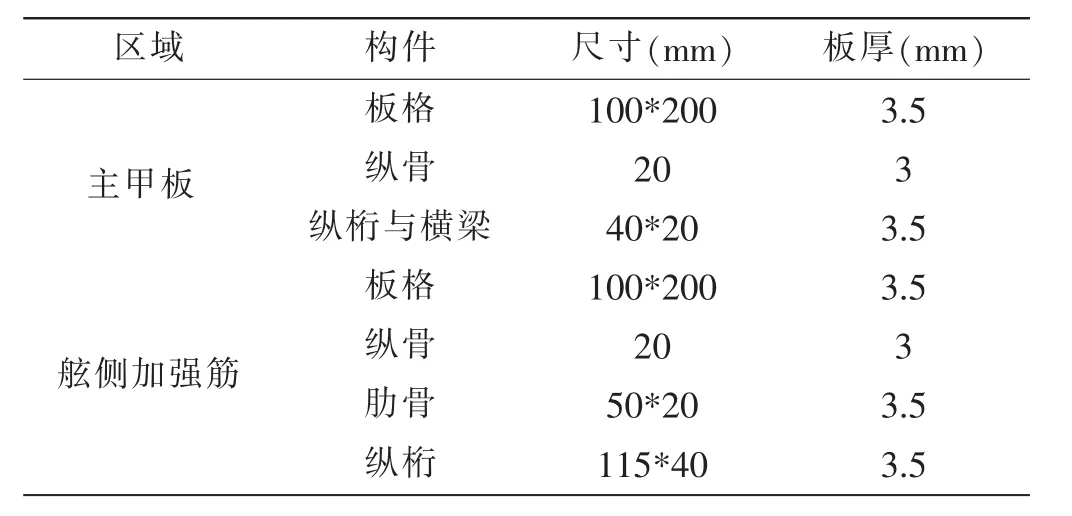
表1 單層板架模型橫截面尺寸Tab.1 Cross sectional dimensions of single grillage

圖1 單層板架模型結構型式圖Fig.1 Structure of single grillage

1.2 坐標系、邊界條件與網格劃分

坐標系原點O位于板架模型端面舷側板與甲板交點，X軸方向為板架長度方向，Y軸方向為寬度方向，Z軸方向為垂向。

板架兩端分別施加剛性面約束，約束于端面中和軸位置的中點；在模型加載端的約束點設置約束Uy=0、Uz=0，并施加一定的Ux作為線位移載荷；在模型約束端的約束點設置約束Ux=0、Uy=0、Uz=0；兩約束點同時施加繞Y軸、大小相同、方向相反的轉角θy。

網格采用縮減積分四節點殼單元，模型大多數區域為四邊形網格，少數區域采用三角形網格過渡。甲板網格尺寸為20 mm×25 mm。

1.3 不同端面轉角下單層板架極限強度對比

板架模型的加載過程為：首先對板架模型兩端面施加轉角θy，使板架彎曲，主甲板部分受壓；保持轉角不變，在加載端施加均布線位移載荷，使板架模型整體受壓。取θy分別為：0、0.003 78 rad、0.017 5 rad（≈1°）和 0.034 9 rad（≈2°），對板架在不同端面轉角下的極限強度進行了系列數值計算，得到不同端面轉角下單層板架的極限載荷如表2和圖2所示。圖3為不同端面轉角下單層板架失效時的主甲板中軸線垂向位移。

由表2和圖2可知，端面轉角越大，單層板架模型的極限載荷越小。由圖3和圖4可知，不同端面轉角下單層板架模型的失效模式有區別：

（1）當θy=0時，板架失效變形為結構整體向上拱起；

（2）當θy=0.003 78 rad時，板架失效變形為結構整體向下凹陷，在原中間艙段部位向上拱起；

（3）當θy=0.017 5 rad時，板架失效變形為結構整體向下凹陷；

表2 不同端面轉角下單層板架模型極限載荷Tab.2 Ultimate load of single grillage at different rotation of end face

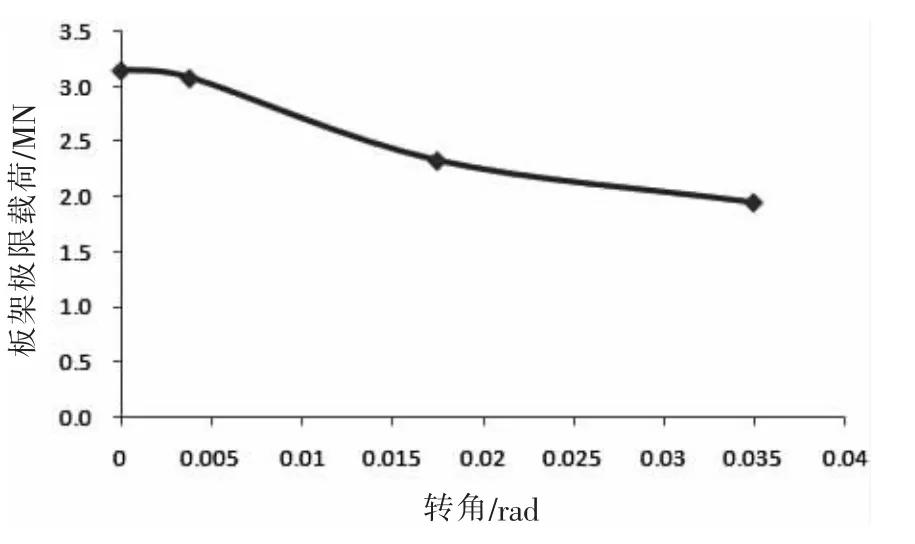
圖2 單層板架極限載荷與端面轉角關系曲線Fig.2 Relation curve between ultimate load and rotation of end face of single grillage

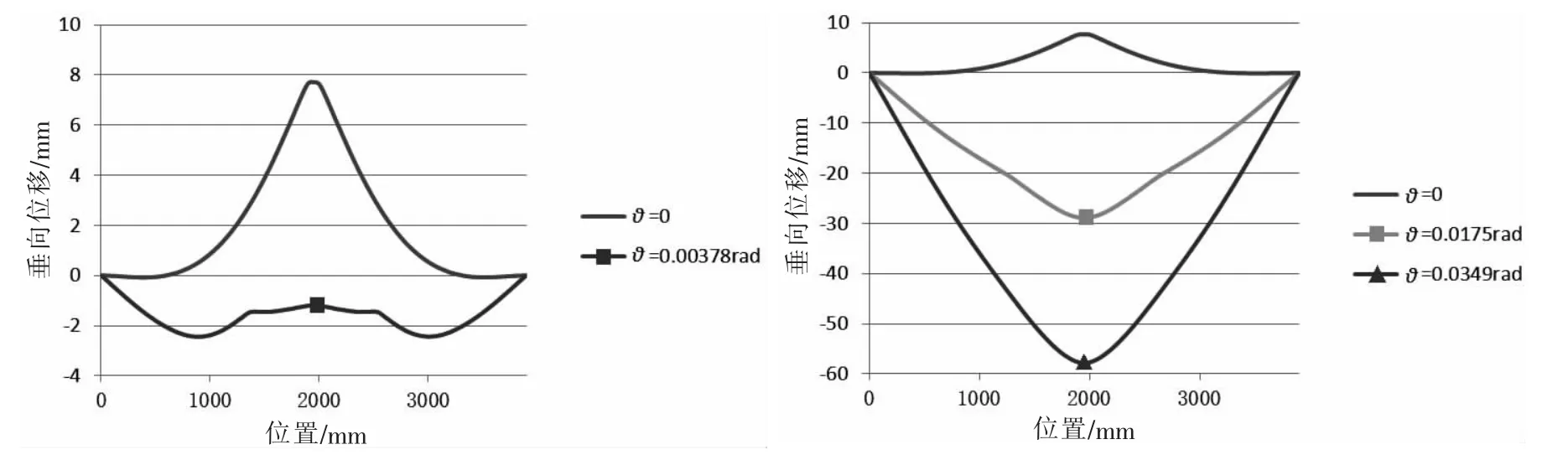
圖3 極限狀態下板架主甲板中軸線垂向位移曲線Fig.3 Vertical displacement degree of central axis of main deck in ultimate state

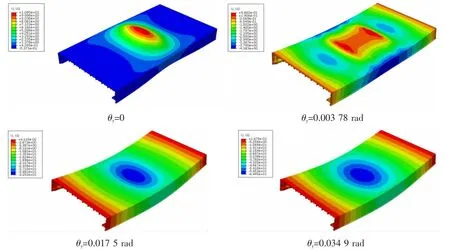
圖4 極限狀態下單層板架模型垂向位移云圖Fig.4 Vertical displacement nephogram of single grillage in ultimate state

（4）當θy=0.034 9 rad時，板架失效變形為結構整體向下凹陷。

由此可見，端面轉角對單層板架的極限承載能力有較大影響：端面轉角越大，板架的極限承載能力越低；不同的端面轉角下板架的失效模式有所不同，若端面無轉角，板架失效時的變形為向上拱起，若端面有轉角，板架失效時的變形為向下凹陷，且轉角越大，變形程度越大。

2 端面轉角對開孔單層板架受壓極限強度的影響研究

本文設計了開孔單層甲板板架模型，選取不同的端面轉角，利用準靜態分析法進行極限強度分析，對比研究了不同端面轉角下開孔單層板架的極限載荷和失效模式。

2.1 開孔單層板架模型設計與網格劃分

開孔單層板架結構模型結構尺寸和材料與1.1節中的單層板架模型相同，在主甲板正中心位置開矩形孔，尺寸為600 mm*480 mm，開孔角隅為半徑R=40 mm的圓角，如圖5所示。板架結構主體采用縮減積分四節點殼單元劃分網格，甲板網格主要尺寸為10 mm×25 mm；在角隅區域采用完全積分四節點殼單元劃分網格，并進行網格細化，細化區域網格邊長2 mm左右。

圖5 開孔單層板架模型示意圖Fig.5 Model of the open single grillage

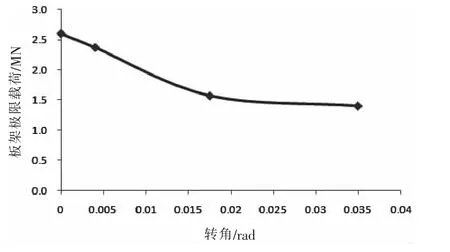
圖6 開孔單層板架極限載荷與端面轉角關系曲線Fig.6 Relation curve between ultimate load and rotation of end face of open single grillage

2.2 不同端面轉角下開孔單層板架極限強度對比

坐標系、邊界條件和加載方式與第1.1節中相同。取 θy分別

為：0、0.004 03 rad、0.017 5 rad和0.034 9 rad。不同端面轉角下開孔單層板架的極限載荷如表3和圖6所示。圖7為不同端面轉角下開孔單層板架失效時的主甲板半側中軸線垂向位移。

表3 不同端面轉角下開孔單層板架模型極限載荷Tab.3 Ultimate load of open single grillage at different rotation of end face

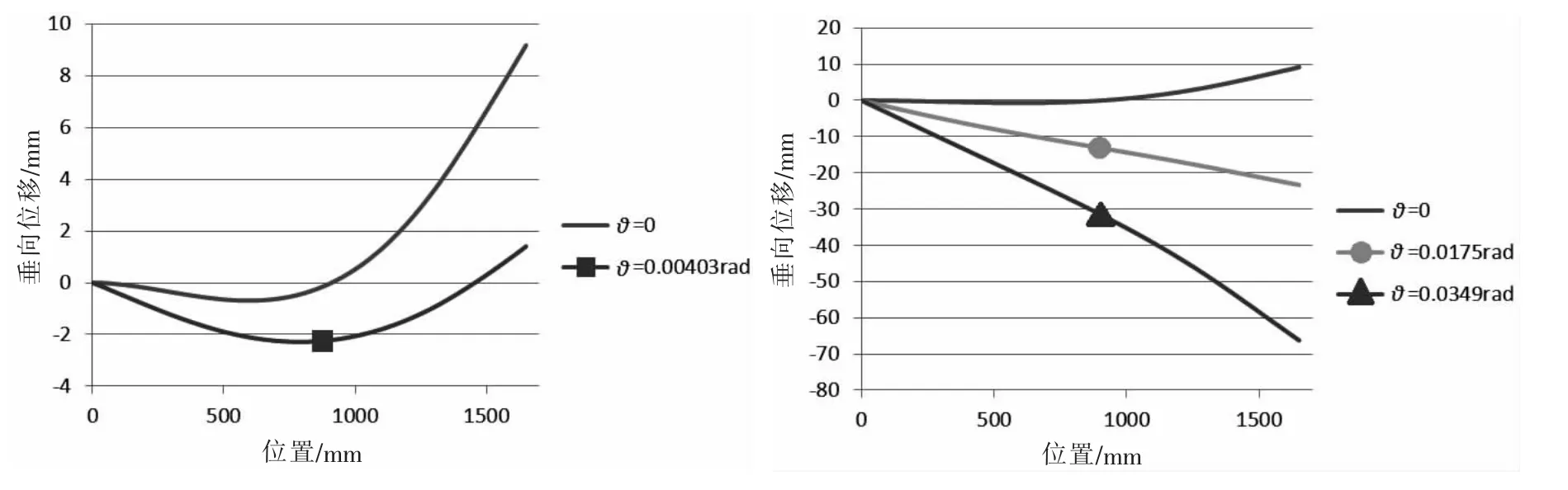
圖7 極限狀態下板架主甲板半側中軸線垂向位移曲線Fig.7 Vertical displacement degree of half-central axis of main deck in ultimate state

由圖6和表3可知，端面轉角越大，開孔單層板架模型的極限載荷越小。由圖7和圖8可知，端面轉角不同的開孔板架模型的失效模式有區別：

（1）當θy為0時，板架失效變形為結構整體向下凹陷，開孔區域向上拱起；

（2）當θy為0.004 03 rad時，板架失效變形為結構整體向下凹陷，開孔長邊區域向下凹陷，開孔短邊區域向上拱起；

（3）當θy為0.017 5 rad時，板架失效變形為結構整體向下凹陷；

（4）當θy為0.034 9 rad時，板架失效變形為結構整體向下凹陷。

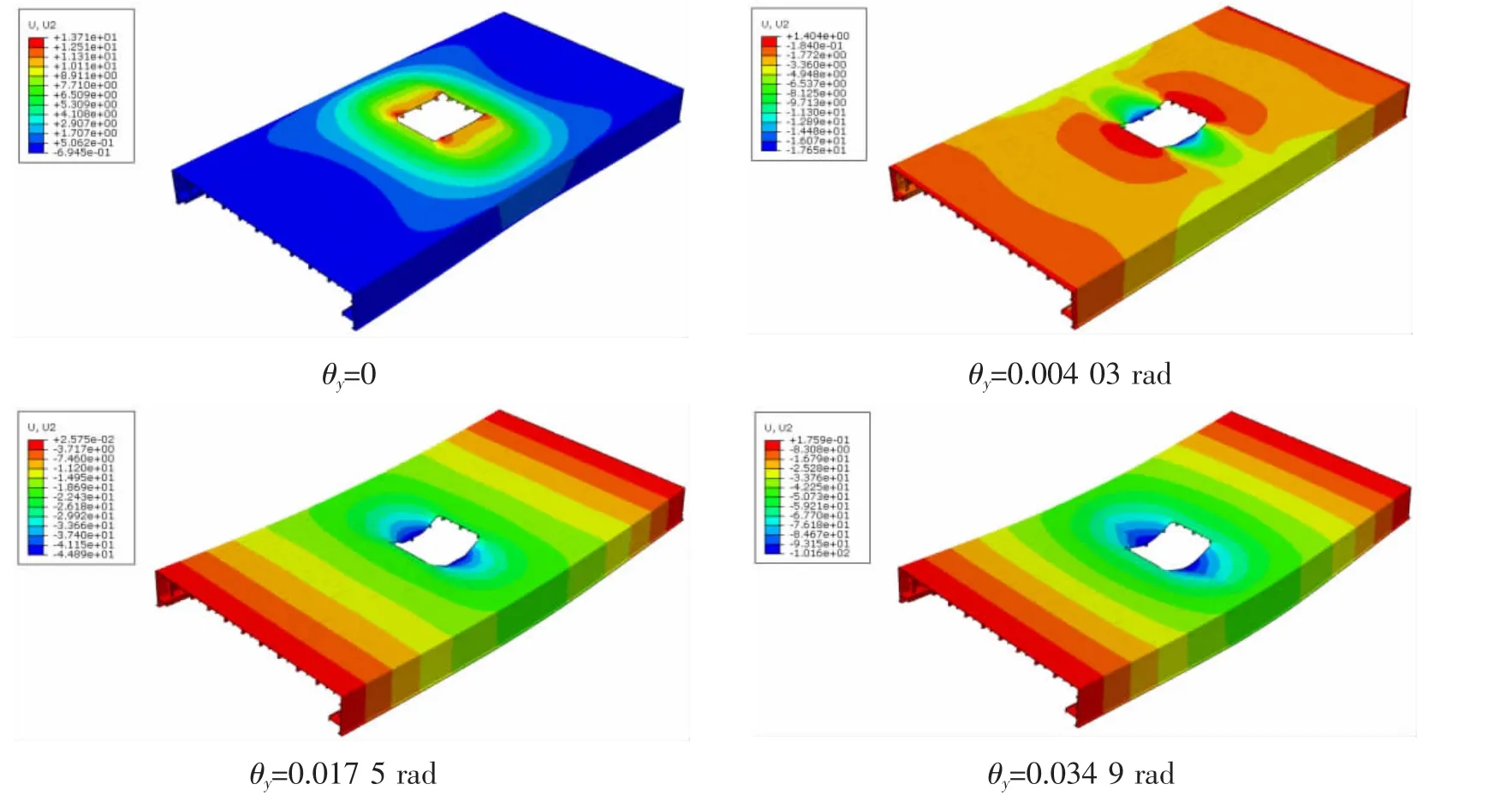
圖8 極限狀態下開孔單層板架模型垂向位移云圖Fig.8 Vertical displacement nephogram of open single grillage in ultimate state

由此可見，端面轉角對開孔單層甲板板架的極限承載能力有較大影響：端面轉角越大，板架的極限承載能力越低；不同的端面轉角下板架的失效模式有所不同，若端面無轉角，板架失效時的變形為整體向下凹陷，開孔區域向上拱起，若端面有轉角，板架失效時的變形為整體向下凹陷，且轉角越大，變形程度越大。

3 端面轉角對雙層板架受壓極限強度的影響研究

本文設計了雙層甲板板架模型，選取不同的端面轉角，利用準靜態分析法進行極限強度分析，對比研究了不同端面轉角下雙層板架的極限載荷和失效模式。

3.1 雙層板架模型設計與網格劃分

雙層板架模型基本尺寸和材料與第2章相同；第二層甲板的縱桁和橫梁等結構基本尺寸與主甲板相同，板厚均為2 mm；板架舷側部位第二層甲板以下保留高度為125 mm的原艙段舷側結構，沿縱向焊接翼板形成加強筋。模型結構型式如圖9所示。板架結構采用縮減積分四節點殼單元劃分網格，甲板網格主要尺寸為10 mm×25 mm。

圖9 雙層板架模型結構型式圖Fig.9 Structure of double grillage

3.2 不同端面轉角下雙層板架極限強度對比

坐標系、邊界條件和加載方式與第1.1節中相同。取 θy分別為：0、0.004 43 rad、0.008 73 rad、0.017 5 rad。不同端面轉角下雙層板架的極限載荷如表4和圖10所示。圖11為不同端面轉角下雙層板架失效時的主甲板中軸線垂向位移。

表4 不同端面轉角下雙層板架模型極限載荷Tab.4 Ultimate load of double grillage at different rotation of end face

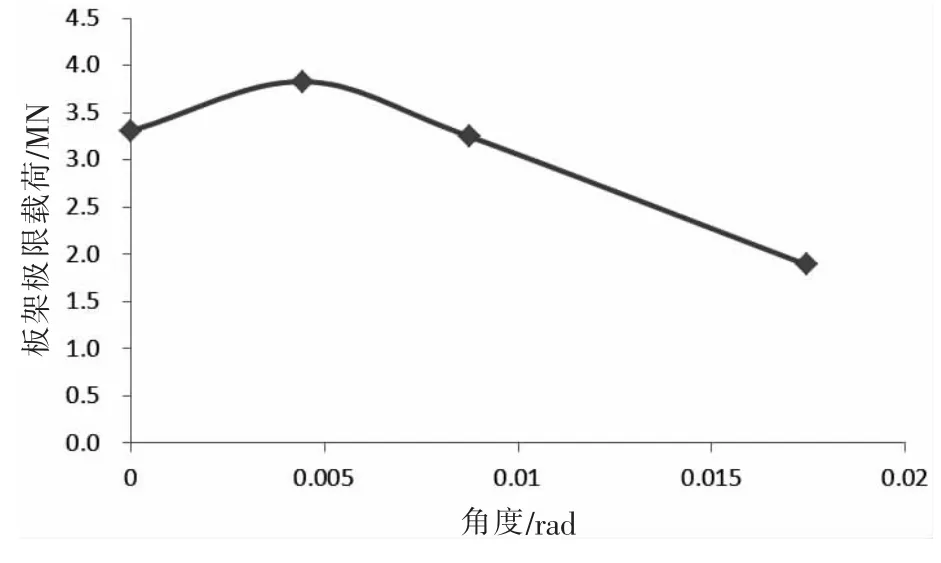
圖10 板架極限載荷與端面轉角關系曲線Fig.10 Relation curve between ultimate load and rotation of end face of open single grillage

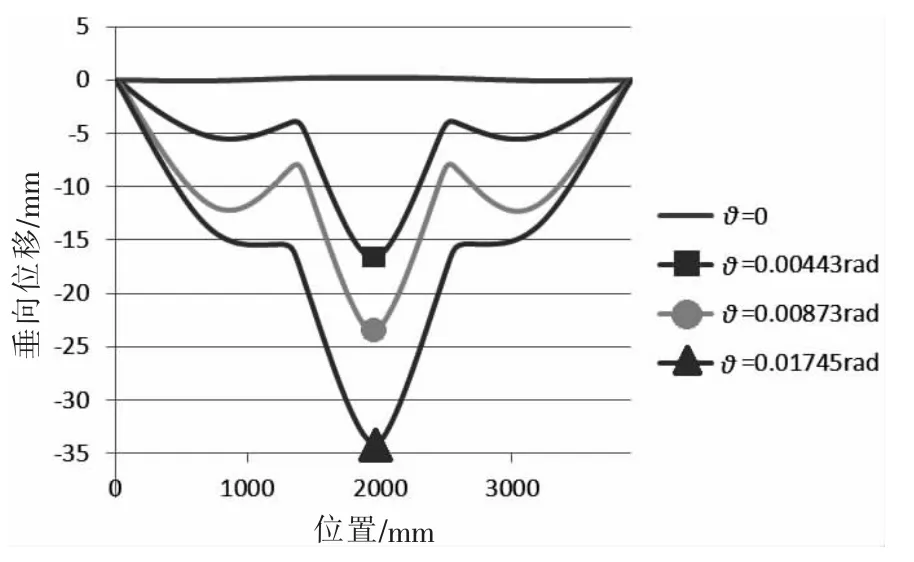
圖11 極限狀態下板架主甲板中軸線垂向位移曲線Fig.11 Vertical displacement degree of central axis of main deck in ultimate state

由圖10和表4可知：當端面無轉角時，雙層板架模型的極限載荷小于θy=0.004 43 rad的雙層板架模型；端面有轉角時，轉角越大，雙層板架模型的極限載荷越小。由圖11和圖12可知，端面轉角不同的雙層板架模型的失效模式有區別：

（1）當θy為0時，失效模式為第二層甲板首先失穩破壞，主甲板尚未失效；

（2）當θy為0.004 43 rad、0.008 73 rad和0.017 5 rad時，失效模式為主甲板首先失穩破壞；失效變形為板架結構整體向下凹陷，中間艙段凹陷程度大于兩端艙段；端面轉角越大，變形程度越大。

由此可見，端面轉角對雙層板架結構極限強度和失效模式有較大影響：端面無轉角的雙層板架的極限承載能力小于有小轉角時的雙層板架，原因是第二層甲板先于第一層甲板失效；對于端面有轉角的雙層板架，轉角越大，板架的極限承載能力越低，但是板架的失效模式相近，均為各艙段分別向下凹陷。

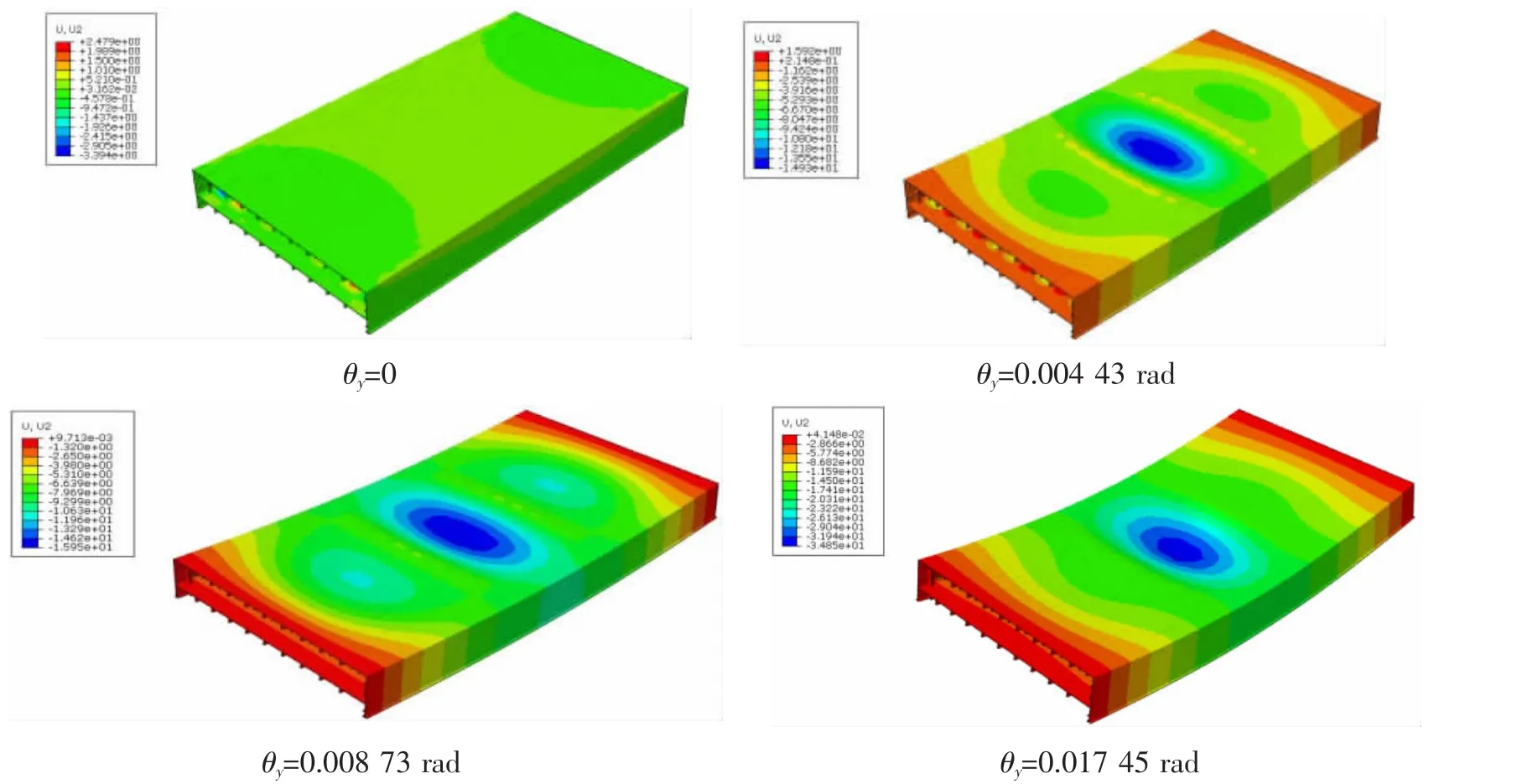
圖12 極限狀態下雙層板架模型垂向位移云圖Fig.12 Vertical displacement nephogram of double grillage in ultimate state

4 結 論

本文采用非線性有限元法，以單層甲板板架、開孔單層甲板板架和雙層甲板板架為研究對象，對比分析板架受壓時，不同的端面轉角下板架的極限載荷和失效模式，研究端面轉角對板架極限強度的影響規律，得出以下結論：

（1）端面轉角對單層板架和開孔單層板架的極限承載能力有影響：端面轉角越大，板架的極限承載能力越低；不同的端面轉角下板架的失效模式有一定區別：若端面無轉角，完整板架失效時的變形為向上拱起，開孔板架失效時的變形為整體向下凹陷，開孔區域向上拱起；若端面有轉角，板架失效時的變形為整體向下凹陷，且轉角越大，變形程度越大。

（2）端面轉角對雙層板架的極限承載能力有影響：端面無轉角時，板架的失效模式為第二層甲板失效，主甲板未失效，極限承載能力小于有小轉角的雙層板架；端面有轉角時，轉角越大，板架的極限承載能力越低；但是板架的失效模式相近。

（3）由以上研究可知，在船體中垂狀態下，甲板板架端面既會產生位移，又會產生轉角，采用板架模型試驗法研究船體中的甲板板架結構極限強度時，不考慮端面轉角的板架模型的極限承載能力和失效模式與考慮端面轉角時有較大的區別，不能反映實船甲板板架的真實響應，因此在試驗中有必要對端面轉角進行模擬。

參 考 文 獻：

[1]吳衛國,袁 天,孔祥韶.船舶甲板結構穩定性實驗與數值仿真研究[J].船舶力學,2017,21(4)：472-479.Wu Weiguo,Yuan Tian,Kong Xiangshao.Experimental and numerical stability analysis of deck grillage[J].Journal of Ship Mechanics,2017,21(4)：472-479.

[2]孔令濱,張火明,方貴盛,田中仁.帶有大開口的船用玻璃鋼夾層板結構力學性能分析[J].玻璃鋼/復合材料,2017,6：5-11.Kong Lingbin,Zhang Huoming,Fang Guisheng,Tian Zhongren.Mechanical properties analysis of FRP sandwich plate frame structure with a large opening[J].Fiber Reinforced Plastics/Composites,2017,6：5-11.

[3]朱漢波,王福華,萬 琪,吳劍國.多跨失穩的縱骨梁柱屈曲載荷—端縮曲線的理論修正[J].船舶,2017,28(1)：35-38.Zhu Hanbo,Wang Fuhua,Wan Qi,Wu Jianguo.Theoretical correction method of load-end shortening curves for longitudinal multi-span unstable overall buckling[J].Ship&Boat,2017,28(1)：35-38.

[4]Wang F,Paik J K,Kim B J,et al.Ultimate shear strength of intact and cracked stiffened panels[J].Thin-Walled Structures,2015,88：48-57.

[5]張錦嵐,李 銘,杜 偉.均布壓力作用下加筋板結構局部補強分析[J].船海工程,2017,46(2)：58-61+65.Zhang Jinlan,Li Ming,Du Wei.On local reinforcement method of stiffened plates under uniform pressure[J].Ship&O-cean Engineering,2017,46(2)：58-61+65.

[6]Shanmugam N E,Zhu Dongqi,Choo Y S,Arockiaswamy M.Experimental studies on stiffened plates under in-plane load and lateral pressure[J].Thin-Walled Structures,2014,80(1)：22-31.

[7]祁恩榮,夏勁松,呂毅寧,劉 超,李政杰,倪 昱.加筋板格高級屈曲分析技術研究及軟件開發[J].船舶力學,2016,20(4)：460-468.Qi Enrong,Xia Jinsong,Lü Yining,Liu Chao,Li Zhengjie,Ni Yü.Technology research and software development on advanced buckling analysis for stiffened panels[J].Journal of Ship Mechanics,2016,20(4)：460-468.