結合高考的高一數學教學例談

梁笛

（陜西師范大學數學與信息科學學院，陜西西安　710062）

本文結合高考要求回歸高一的基礎教學，以北師大版高中數學必修一內容為例從教師用好教材變式教學，學生用好教材舉一反三的角度談談教師如何在起始年級的數學教學中幫助學生構建良好的數學知識體系，培養學生優秀的數學思維品質，建立學生科學的數學學習方法。

1　教師如何用課本教

1.1　依據教材而不拘泥于教材

公平、公正地對待各個版本，不刻意向某一版本傾斜，在平時的教學中宜參考不同版本，整合各版本引入、例題、習題方面的優點，選擇適合本班學生認知水平、接受能力的內容在課堂教學中使用。

例如：《北師版高中數學必修一第三章第六節》在進行處理的時候以繁瑣、復雜的運算和生硬枯燥的表格呈現出三種函數的增長，缺乏直觀性、趣味性，經常讓教師不知如何指導學生使用這節內容，而往往學生也會在這節課學完以后只是機械的記住：當a＞1，指數函數y=ax與對數函數y=logax都是增函數，a越大，函數值的增長就越快；當 x＞0，n＞1時，冪函數 y=xn也是增函數，并且當x＞1時，n越大其函數值的增長就越快。當三類函數一起比較時，當x足夠大時，必有指數函數的增長最快，人們稱這種現象為“指數爆炸”。

學生對于三種函數增長變化的印象僅僅停留于此，可能沒有更多的興趣進一步去研究它們了。

但是湘教版在處理這節課的時候就精彩有趣很多，我們一起欣賞一下它的引入。

引例：以冪函數模型圖象變化快慢切入。

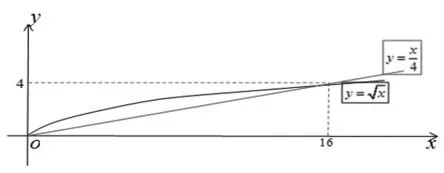
圖1

這樣的引用通俗易懂，妙趣橫生，將學生代入利用圖象研究函數的氛圍之中，后續課程的鋪開便顯得很自然。

1.2　以課本例題和習題為基本題根，進行變式教學，高站位，低起點

很顯然，這道題是讓學生從初中反比例函數的圖象出發，直觀感受單調性的。但是教師必須在學生的直觀上建立嚴謹的證明，讓學生從高中單調性定義出發給出此題單調性的嚴格證明，并進行以下的變式練習。

1.3　講清課本基本定義并進行適合不同學生層次的引申

如函數的單調性定義：在函數y=f（x）的定義域的一個區間A上，如果對于任意兩數x1，x2∈A，當x1＜x2時，都有 f（x1）＜f（x2），那么，就稱函數 y=f（x）在區間 A上是增加的。

對于這樣的定義，教師應該引導學生用等價的數學式子表達為：對于定義在A上的函數f（x），設x1，x2∈A，則有：

這就達到了在基礎要求之上的第一層次的提升，而對于層次更好的學生或者隨著學習的深入學生的思維得到提升以后，可以引導學生給出第二層次的探究。

2　學生如何用課本學

2.1　學會評價并欣賞課本解題思路，善于聯系貫穿各個知識點

x∈[-1，2]的最大值與最小值。

2.2　總結、聯系、整理由課本引出的變式練習

學生通過一段時間的積累便能發現這些題目之間的聯系，同時在這種發現中展開了聯想與想象的能力，也能更深刻的體會我們通常所說的“分離系數法”是怎樣的一種方法，為何需要想到并且應用這種方法解題？這就比老師直接告訴學生方法要印象深刻得多，也讓學生體會了更多的成就感，體會了發現數學方法的樂趣。

2.3　重視教材后面的閱讀資料

在閱讀資料中感受數學的文化魅力和應用價值，比如在進行了對數運算的學習之后我們可以通過對數換底進行大數的估算和比較，這不就是對數引入的初衷嗎？閱讀完相關材料后教師可以提供學生這樣的問題：

已知 lg2=0.3010，1g3=0.4771（1）估計 2100的大小；（2）比較 2100與 365的大小。

解析：（方法一）設x=2100，等號兩邊同取以10為底的對數，得：

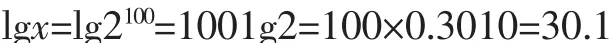
所以 x=1030.1=1030×100.1

（方法二）利用對數的常用恒等式alogaN=N

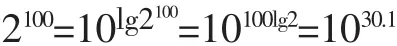
同理可以估算365的大小，進而很容易比較這兩個數。一般計算器不好解決的計算問題，我們可以通過數學算法給出解答，這種數學應用意識和應用能力的培養建立了學生學習數學的興趣和信心。

如果學生還想進一步探究，可以嘗試把自己平時學習中的發現撰寫成數學小論文，對學生的數學表達能力是很好的鍛煉。也讓學生在具體的“做”中學數學、感受數學、應用數學。

用好了教材，教師才能在課堂上教出新意，教出方法；用好了教材，學生才能在學習中學到方法，學出能力.教與學才充滿了創造和樂趣.

[1]黃坪，尹德好.高中數學題根[M].上海：華東師范大學出版社，2013.

[2]嚴士健，李延林.普通高中課程標準實驗教材數學1（必修）[M].北京：北京師范大學出版社，2004.

[3]張景中，黃楚芳.普通高中課程標準實驗教材數學1（必修）[M].湖南：湖南教育出版社，2011.

[4]張揚文.高考數學你真的掌握了嗎？函數[M].北京：清華大學出版社，2014.