定積分的五種求法

■甘肅省白銀市第一中學(xué)　胡貴平

定積分是新課標(biāo)的新增內(nèi)容,其中定積分的計(jì)算是重點(diǎn)考查的考點(diǎn)之一,下面通過(guò)例題來(lái)看定積分計(jì)算的五種常用方法。

一、定義法

分析：用定義法求積分可分四步:分割,以直代曲,作和,求極限。

二、基本定理法

分析：可先求出原函數(shù),再利用微積分基本定理求解。

解：函數(shù)y=x2+2x+1的一個(gè)原函數(shù)

三、幾何意義法

分析：利用定積分的意義是指曲邊梯形的面積,只要作出圖形就可求出。

圖1

四、性質(zhì)法

求下列定積分:

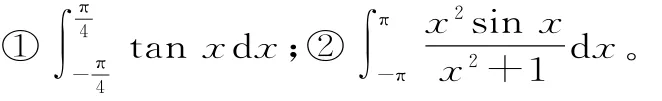
分析：對(duì)于①用微積分的基本定理可以解決,而②的原函數(shù)很難找到,幾乎不能解決。若運(yùn)用奇偶函數(shù)在對(duì)稱區(qū)間的積分性質(zhì),則能迎刃而解。

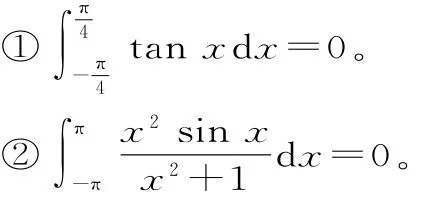
五、綜合法

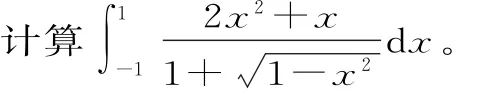
分析：由于積分區(qū)間關(guān)于原點(diǎn)對(duì)稱,因此首先應(yīng)考慮被積函數(shù)的奇偶性。

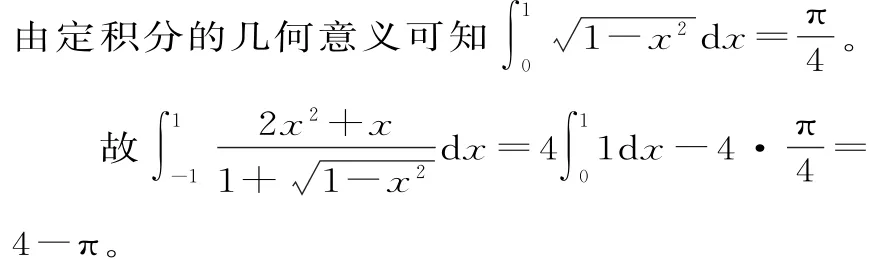
通過(guò)對(duì)這五個(gè)例題的分析,我們應(yīng)該牢固記住如何求定積分的方法,懂得在什么情況下該用何種方法解決問(wèn)題。