一類隱零點問題的解題策略

■東北師范大學附屬中學　劉彥永

近年來,高考數學壓軸題的熱點聚焦在了函數的零點和極值點問題。筆者在教學實踐中發現同學們對隱零點(零點不可求)問題沒有系統的解決辦法,常常望而生畏,不知所措。本文通過下面的典型題目探討這類問題的三種基本解法,以明確這類問題的解題策略,提高解題效率。

題目1：設函數f(x)=ex-ax-2。

(Ⅰ)求f(x)的單調區間;

(Ⅱ)若a=1,k為整數,且當x＞0時,(x-k)f'(x)+x+1＞0,求k的最大值。

本題是2012年全國新課標卷Ⅱ文科第21題,題目限制條件比較新穎,采用設而不求的解法非常有效,這類題型的練習對同學們的思維有一定的啟發性。

解析：(Ⅰ)函數f(x)的定義域為R,且f'(x)=ex-a。

當a≤0時,f'(x)＞0,f(x)在R上是增函數,f(x)的單調遞增區間是R;

當a＞0時,令f'(x)=ex-a=0,得x=lna。

令f'(x)=ex-a＞0,得x＞lna,所以f(x)在(lna,+∞)上是增函數;

令f'(x)=ex-a＜0,得x＜lna,所以f(x)在(-∞,lna)上是減函數。

故f(x)的單調遞增區間是(lna,+∞),單調遞減區間是(-∞,lna)。

(Ⅱ)解法1：(分離參數、設而不求,轉化為函數最值問題)

若a=1,則f(x)=ex-x-2,f'(x)=ex-1。

所以(x-k)f'(x)+x+1=(x-k)(ex-1)+x+1=x(ex-1)+x+1-k(ex-1)。

當x＞0時,(x-k)f'(x)+x+1＞0等價于x(ex-1)+x+1-k(ex-1)＞0。

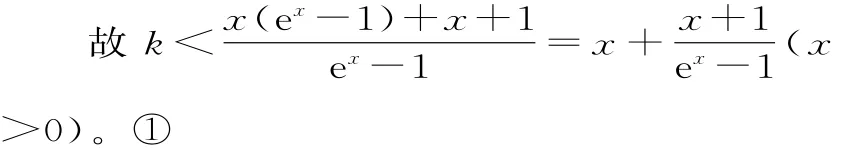
由于①式等價于k＜g(α)=α+1∈(2,3),故整數k的最大值為2。

解法2:(分類討論,轉化為函數最值問題)

當x＞0時,(x-k)f'(x)+x+1＞0等價于:(x-k)(ex-1)+x+1＞0。②

令g(x)=(x-k)(ex-1)+x+1(x＞0),g'(x)=(x-k+1)ex。

(1)當k≤1時,g'(x)＞0恒成立,g(x)在(0,+∞)上單調遞增,g(x)＞1＞0,符合題意。

(2)當k＞1時,若x∈(0,k-1),則g'(x)＜0;若x∈(k-1,+∞),則g'(x)＞0。

故g(x)在(0,k-1)上單調遞減,在(k-1,+∞)上單調遞增。

由于②式等價于g(x)min=g(k-1)=k+1-ek-1＞0。

令h(k)=k+1-ek-1(k＞1),h'(k)=1-ek-1＜0,h(k)在(1,+∞)上單調遞減。

且h(2)=3-e＞0,h(3)=4-e2＜0,故整數k的最大值為2。

由(Ⅰ)知,函數h(x)=ex-x-2在(0,+∞)單調遞增。

而h(1)=e-3＜0,h(2)=e2-4＞0,所以h(x)在(0,+∞)上存在唯一的零點。

故g'(x)在(0,+∞)存在唯一的零點,設此零點為α,則α∈(1,2)。

當x∈(0,α)時,g'(x)＜0;當x∈(α,+∞)時,g'(x)＞0。

所以g(x)在(0,+∞)的最小值為g(α)。

又由g'(α)=0,可得eα=α+2,所以

解法3:(巧妙換元、數形結合,轉化為切線問題)

當x＞0時,(x-k)f'(x)+x+1＞0等價于x(ex-1)+x+1-k(ex-1)＞0。

令t=ex∈(1,+∞),則問題等價于tlnt+1-k(t-1)＞0,即tlnt+1＞k(t-1)。

令g(t)=tlnt+1(t＞1),g'(t)=lnt+

問題等價于函數g(t)=tlnt+1的圖像恒在過定點(1,0)的直線y=k(t-1)的上方。

作出草圖即知臨界值為過(1,0)作g(t)=tlnt+1的切線。

設切點坐標為(α,αlnα+1),則k切線=即lnα-α+2=0。

k切線=lnα+1=α-1∈(2,3),故整數k的最大值為2。

題目2：已知函數f(x)=axex-1,g(x)=lnx+kx。

(Ⅰ)求函數g(x)的單調區間;

(Ⅱ)當k=1時,f(x)≥g(x)恒成立,求a的取值范圍。

當k≥0時,g'(x)＞0,g(x)在(0,+∞)上是增函數;

(Ⅱ)解法1：(分離參數、設而不求,轉化為函數最值問題)

當k=1時,f(x)≥g(x)恒成立,即axex-1≥lnx+x恒成立。

故lnt+t=0,即t=e-t。

當x∈(0,t)時,p(x)＞0,h'(x)＞0;當x∈(t,+∞)時,p(x)＜0,h'(x)＜0。

h(x)max=h(t)=1。

解法2：(分類討論,轉化為函數最值問題)

當k=1時,f(x)≥g(x)恒成立,即axex-lnx-x-1≥0恒成立。

(1)當a≤0時,h'(x)＜0恒成立,h(x)在(0,+∞)上單調遞減,h(1)=ae-2＜0,不符合題意。

(2)當a＞0時,令p(x)=axex-1(x＞0),p(x)在(0,+∞)上單調遞增。

x∈(0,t)時,h'(x)＜0;x∈(t,+∞)時,h'(x)＞0。

h(x)min=h(t)=atet-lnt-t-1=-lnt-t=lna≥0,故a≥1。

解法3:(數形結合,轉化為公切線問題)

當k=1時,f(x)≥g(x)恒成立,即axex-1≥lnx+x恒成立。

分別研究f(x)=axex-1和g(x)=lnx+x在(0,+∞)上的圖像。

當a≤0時,axex-1≥lnx+x顯然不恒成立。

當a＞0時,因為f'(x)=a(x+1)ex＞0,f″(x)=a(x+2)ex＞0,且g'(x)=+ 1＞0,g″(x)=-＜0,所以兩個函數的草圖(圖1)和臨界時的圖像(圖2)如下:

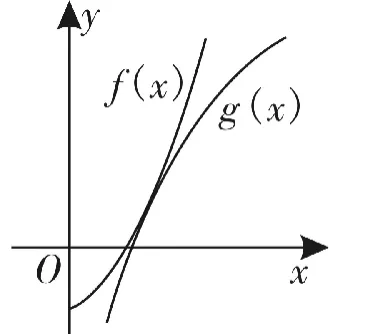
圖2

圖1

因此,只需找到臨界狀態對應的a即可。設臨界時兩曲線的公共點的橫坐標為t,則有消去a得(t+1)(lnt+t)=0,即lnt+t=0。故atet-1=lnt+t=0,即atet=1,取對數有lna+lnt+t=0,得a=1。根據圖像變化情況知a≥1符合題意。

隱零點問題是高考的一類重點和難點問題,解決此類問題主要有分離參數、分類討論和數形結合三種方法,三種方法各有千秋,應具體問題具體分析。一般首選分離參數的方法,因為這樣能將問題轉化為不含有參數的函數的最值問題,直接降低了解答的難度。對于不易或不能分離參數的問題可采用分類討論的方法。對于選擇題或者填空題,我們可以利用技巧等價轉化并應用數形結合快速得到答案。