掌握技巧，讓導數運算飛起來

■江蘇省張家港職業教育中心校　韓文美

導數的運算關鍵是熟記導數基本公式,特別是常見函數的導數公式,掌握兩個函數和、差、積、商的求導法則,掌握簡單復合函數的導數公式,以及能夠綜合運用各種法則求比較復雜的函數的導數等。而在實際的導數運算中,經常可以根據被導函數的特征,通過一定的技巧,更為快速、流暢、簡捷地解決導數的運算問題,真正讓導數運算飛起來。

1.分式問題——裂項法

分析：常見思維是根據商式利用商的求導法則進行求導,這樣操作計算量大而復雜,容易出錯。而先根據分式通過裂項化簡,再進行求導,就顯得簡單且容易處理。

解：原函數可變形為f(x)=x3+2sinx

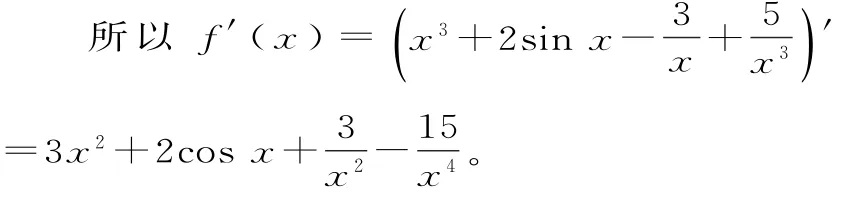
點評:一般地,如果函數的解析式整體為分式,而分子分母為自變量x的多項式,為了減少運算量,可以考慮將解析式裂成多個較為簡單的代數式的和差形式后再來求導。

2.根式問題——有理化

分析：常見思維是直接根據兩和式中對應的商,利用商的求導來處理。而若觀察該關系式,其分母含有根式,先通過分母有理化加以化簡,進而再進行求導,就可以大大簡化求解過程。

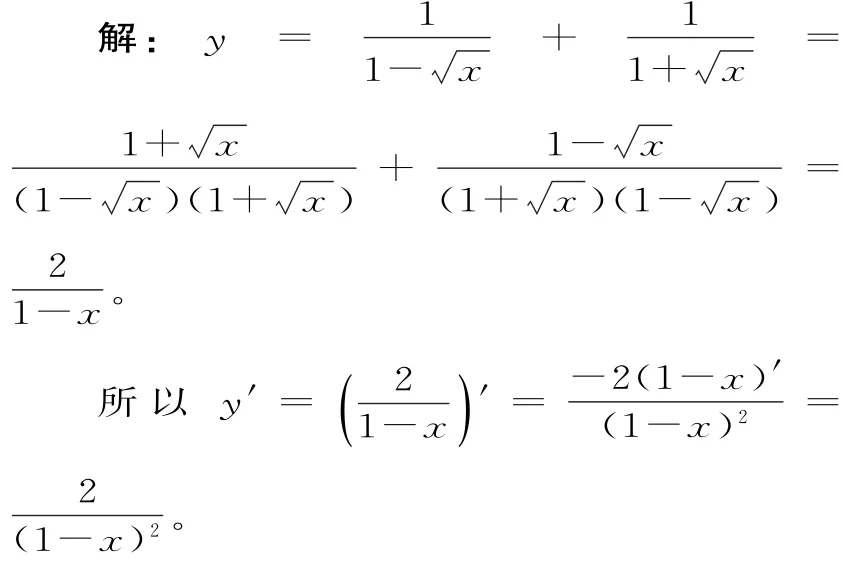
點評:有理化處理求導問題一般有兩種形式:一是如果分子中含有根式,則利用分子有理化,二是如果分母含有根式,則利用分母有理化。有理化的目的就是簡化過程,使得求導更為簡捷方便。

3.積式問題——展開法

設函數f(x)=(2x3-3)(x2-5),則f'(x)等于。

分析：常見思維是利用積的求導法來完成第一次求導,然后對相關項再次求導,此法相對來說計算量大,容易出錯。而先將兩個整式的積利用多項式的乘法加以展開,再求導,其運算過程將會大大簡化。

解：f(x)=(2x3-3)(x2-5)=2x5-10x3-3x2+15。

故f'(x)=(2x5-10x3-3x2+15)'=10x4-30x2-6x。

點評:對于此類積式的求導問題,要注意平方差公式、立方和公式等的應用,在可能的情況下,應盡量少用甚至不用乘積的求導法則,以減少計算量,優化過程。

4.對數式問題——拆分法

分析：如果直接求導,涉及對數的導數、復合函數的導數等,相當復雜,根本無從下手。而若先根據函數特點,利用對數運算法則進行適當拆分處理再進行求解,則另辟蹊徑,曙光在望。

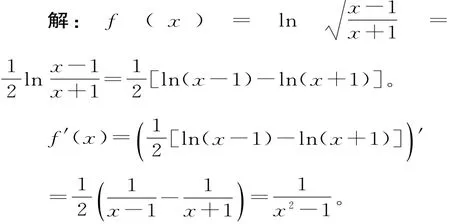
點評:對于此類對數式的求導問題,應先根據對數式的結構特點,適當地對函數式中的項進行合理拆分,然后再各個擊破,從而達到簡化運算,提升效率的目的。

5.三角式問題——恒等變形

分析：如果直接求導,則需要利用積、商的求導法則,三角函數的導數等來處理,計算量非常大,且易出錯。而先對三角函數式進行三角恒等變形,再利用公式和運算法則處理,可減少運算量,提高運算速度,減少差錯。

所以y'=(sinx)'=cosx。

點評:有的三角函數雖然表面形式為函數的商的形式,但在求導前利用三角恒等式將函數先化簡,然后進行求導,可以避免使用商的求導法則,減少運算量。

6.規律式問題——構造法

已知函數f(x)=x(x2+1)(x3+2)…(x2018+2017),則f'(0)=。

分析：常見思維是對有一定規律性的函數f(x)進行求導,再代入求解對應的導數值問題,此法計算量比較大,而且容易出錯。而根據函數中規律式的性質,通過構造函數f(x)=xg(x),利用求導來轉化,可以有效減少計算量,提升解題效益。

解：設g(x)=(x2+1)(x3+2)…(x2018+2017),則g(0)=2017！(n！表示1×2×3×…×n)。

又f(x)=xg(x),兩邊求導,可得f'(x)=g(x)+xg'(x)。

所以f'(0)=g(0)+0×g'(0)=g(0)=2017！。

點評:本題通過導數的四則運算法則,結合有規律函數式的性質,求導后加以求值。以上方法通過重新組合,巧妙地將多個因式之積看成兩個因式之積加以構造,方法巧妙,解決問題快捷有效。

在做導數運算時,我們除應牢記和運用好導數公式外,還要認真觀察函數的結構特征,積極地進行聯想化歸,抓住問題的本質,把解題思路放開,利用更好更快的運算技巧來分析,避免繁雜的運算過程,減少不必要的錯誤。