基于數學活動經驗積累的教學實踐研究
——以《可能性大小》為例

江蘇南京致遠外國語小學　　劉　　媛

數學課程標準對“數學活動經驗”的內涵并沒有提出明確的解釋，因此引發了眾多不同的解讀。以下筆者將結合所教的《可能性大小》公開課，分享在磨課過程中對培養學生數學基本活動經驗的認識和感悟。

一、數學基本活動經驗的特征

1.個體性特征

【教學片段1】感悟“一定”“不可能”。

老師出示2個同樣大小的不透明的袋子，①號袋里放2個紅球，②號袋里放1個藍球、1個黃球，并向學生說明：這些球除了顏色不同外，形狀、大小、材質等都完全相同。

提問：如果摸到紅球算勝利，你會選哪個袋子？為什么？

生：選①號袋，因為兩個都是紅球，肯定是摸到紅球。

小結：①號袋里2個都是紅球，摸出球的情況是確定的，任意摸一個，一定是紅球。

提問：在②號袋里任意摸一個球，會摸到紅球嗎？為什么？

生：不可能，因為②號袋里沒有紅球。

片段中，學生通過和老師的問答，感悟“一定”“不可能”，這并不是系統的“數學知識”，而是學生通過觀察和思考獲得的感受和體驗。學生憑借自身的認知經歷，對將要發生的結果進行感性的概括，這是學生經歷了活動后在不自覺中形成的新的認識。這里的認識既包含了學生已有的認識，又有在融入了學生個性特征基礎上所積累到的新知識。

2.多樣性特征

【教學片段2】摸球游戲，感悟“可能”。

師：老師把這2個球（1紅、1黃）放進口袋里，如果摸到紅球，女生贏，摸到黃球，男生贏。這個游戲公平嗎？為什么？

生1：個數相同，一半對一半的概率。

生2：紅球和黃球各一個，各占50%。

師：從這個口袋中任意摸一個球，摸球前，我們可以預測：可能摸到紅球，也可能摸到黃球。也就是，男生贏和女生贏的可能性是相等的。

小組活動：

（1）在口袋里放入1個紅球和1個黃球，組員摸球，一共摸10次，摸后放回。

（2）記錄員用相應顏色的水彩筆依次整齊地將結果涂在實驗記錄卡（一）上。

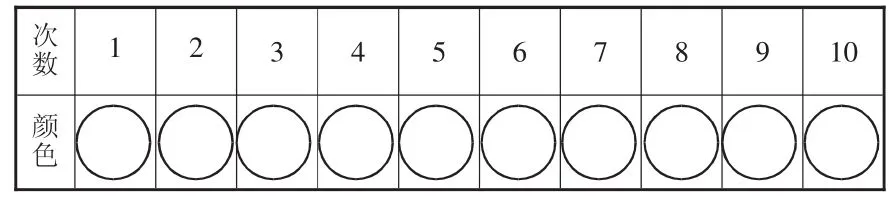
實驗記錄卡（一）

組長匯報摸球結果，板貼展示（如圖1）。

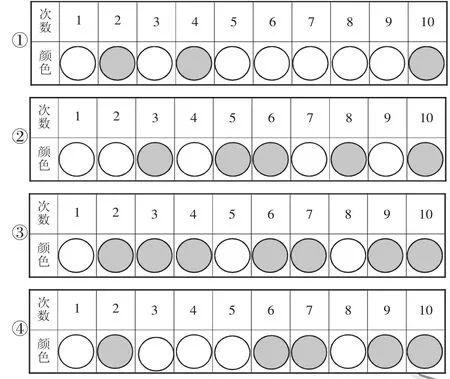
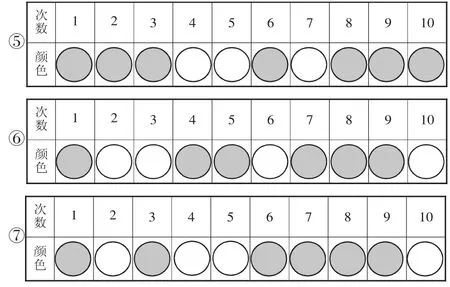
圖1

提問：出現這些結果合理嗎？

小結：在摸球之前，預測摸到紅球和黃球的可能性是相等的，但這并不能代表摸球的結果一定相等，因為每一次摸到紅球或者黃球的結果是不確定的，所以，出現這些結果都是合理的。

初授時，本環節的設計被零散地分成了三部分：“裝有1個紅球和1個黃球的口袋”“裝有2個紅球的口袋”“裝有2個黃球的口袋”，之前的設計多是教師和個別幾個學生對話，相對單一。對于學生來說，感悟“一定”“不可能”和“可能”更需要經驗交流的過程，所以經過多次磨課，筆者將本環節修改為上述“教學片段1”和“教學片段2”，通過兩次預判，讓學生在群體經驗中認識新知，并延伸出“出現這些結果是否合理”的追問，充分發揮數學活動經驗的多樣性特征。

3.發展性特征

【教學片段3】結果比較，內化認識。

觀察：結合教學片段2中實驗記錄卡（一）的摸球結果，如果豎著看每組的摸球情況，第一次可能摸到什么球？第幾次摸到紅球？第幾次摸到黃球？摸球前能知道嗎？

追問：如果老師現在再摸一次，結果會是怎樣的？

讓學生觀察、比較全班的摸球情況，分別從橫向與縱向角度進行對比，豐富學生對“可能”的認識的直觀感受。學生的回答步步逼近，不斷從小組、班級同學的分享中獲得新的認識，促進了學生的數學活動經驗從感性水平上升到理性水平。

4.內隱性特征

【教學片段4】摸牌游戲，體會可能性大小。

活動要求：

（1）把4張撲克牌打亂次序后反扣在桌上。每人摸之前組長先把牌混勻，摸出后告訴記錄員是什么牌。

（2）根據組長報的花色，畫“正”字記錄在實驗記錄卡（二）里，并統計出結果。

（3）按號碼次序摸牌，每次摸好后把牌反扣并放于桌面，一共摸30次。

實驗記錄卡（二）

活動后組長匯報摸牌情況，教師根據各組長的匯報將本班情況進行匯總（如圖2）。

聚光器將太陽光反射集中在接收器上。分析聚光器性能的關鍵參數是聚光器的直徑dcon，鏡面反射率ηm和太陽輻射強度I。本系統聚光器直徑取10 m，鏡面反射率取92%。使用雙軸跟蹤太陽的情況下，聚光器接收太陽光的總能量Q1為

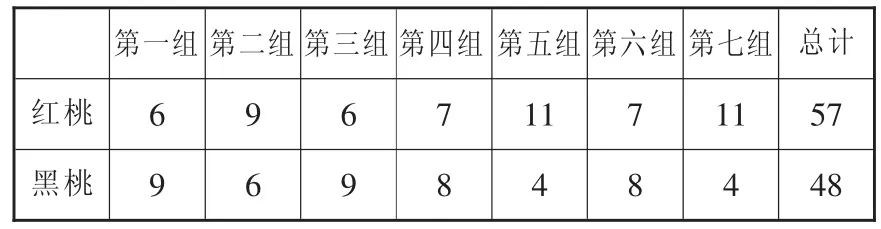
圖2

提問：觀察表格，比較摸到紅桃和黑桃的次數，你有什么發現？摸牌的結果能說明什么？

小結：在摸牌之前，根據牌的花色，我們可以預計摸到紅桃的次數多，摸到黑桃的次數少。這并不能代表摸牌的結果一定是這樣，黑桃牌數量雖然少，但因為每一次摸牌的結果不確定，黑桃也有可能被摸到。所以，出現這些結果都是合理的。從這個實驗，我們也可以看出：事件發生的可能性是有大小的。

通過上述教學環節可以看出，學生的數學活動經驗如果僅僅停留在感性層面是不易被學生把握到的，所以筆者在多次磨課過程中，讓學生通過摸牌游戲自己獲得數據，在對數據對比分析的過程中體會可能性的大小，從而讓學生的隨機意識得以外顯。

5.實踐性特征

【教學片段5】裝球游戲。

活動要求：往口袋里裝6個球，要求從中任意摸1個球，可能是綠球。

交流不同的裝法（如圖3）：

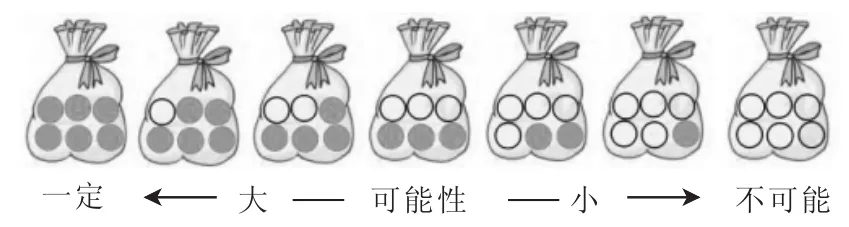
圖3

教師小結，同步呈現“大——可能性——小”。

增加6個球都是綠球的袋子及沒有綠球的袋子，引導學生觀察不同的裝球方法，溝通“一定”“可能”“不可能”之間的關系。

二、數學基本活動經驗的落實

1.在經歷中形成經驗

在經歷數學活動的過程中，教師需要引導學生在活動的每個環節中去經歷，以形成不同的感受。《可能性大小》一課中，多數學生在實際生活中都對可能性有一些感性認識，具有判斷簡單隨機事件的可能性大小的直觀經驗，這些經驗是學生學習這部分內容的基礎。在教學中，筆者特別注意激活學生的已有經驗，并引導他們將已有經驗上升為理性的數學思考。如在討論“從紅桃A、紅桃2、紅桃3、黑桃4這4張牌中任意摸出1張，是摸出紅桃的可能性大，還是摸出黑桃的可能性大”這個問題時，側重于引導學生基于所有可能出現的結果種數做出合乎邏輯的判斷。這些活動都有助于學生將已有的經驗“數學化”，從而逐步形成對可能性及其大小的理性認識。

2.在運用中提升經驗

要想讓學生把在活動中獲得的“看不見、摸不著”的經驗內化于自身，就需要將整個學習過程中所獲得的經驗清晰化、條理化。筆者在教學片段5的操作活動之后，幫助學生在交流中逐步澄清“可能性大就是必然，可能性小就是不可能”以及“理論判斷與實驗結果一定完全一致”等原先模糊的認識，從而使他們更加全面地體驗隨機現象的特點，提升已有的數學活動經驗。

3.在反思中鞏固經驗

筆者在設計“可能性大小”一課時，緊扣“在具體情境中體驗事件發生的隨機性”以及“通過試驗、游戲等活動，感受隨機現象結果發生的可能性是有大小的”這兩個基本目標，引導學生主動參與摸球、摸牌、裝球等蘊含隨機現象的活動，通過經歷多個實踐活動，學生初步掌握判斷可能性大小的思考方法，感悟隨機現象的特點，體驗不確定的思維方式。?

【參考文獻】

[1]危木榮.基本活動經驗的特征及分類［J］.福建教育（小學版），2012（6）.

[2]荀步章．幫助學生積累基本活動經驗的策略[J]．小學數學教育，2015（1-2）．

[3]劉靈芝．幫助學生積累豐富的基本活動經驗[J]．小學數學參考，2014（7）．