矩形b-度量空間中壓縮映象的公共耦合不動(dòng)點(diǎn)定理

劉麗亞,谷 峰

(杭州師范大學(xué)應(yīng)用數(shù)學(xué)研究所;數(shù)學(xué)系,浙江杭州 310036)

1　引言和預(yù)備知識(shí)

Branciari[1]首次引入了矩形度量空間的概念,并給出了此空間中的Banach壓縮映象定理.此后,很多學(xué)者在此空間中研究了其他不同壓縮條件下的不動(dòng)點(diǎn)問(wèn)題[2?11],同時(shí)也給出了Banach壓縮定理和Kannan型不動(dòng)點(diǎn)定理在矩形b-度量空間中的一些應(yīng)用.本文受到上述結(jié)論的啟發(fā),將在矩形b-度量空間中討論耦合重合點(diǎn)和公共耦合不動(dòng)點(diǎn)的存在性和唯一性問(wèn)題,得到了一類新的公共耦合不動(dòng)點(diǎn)定理,在很大程度上推廣了相關(guān)文獻(xiàn)[12]的一些結(jié)果.

在介紹主要結(jié)果之前,先介紹一些基本概念和已知結(jié)果.

定義1.1[1]設(shè)X 是非空集,d:X×X→[0,+∞),且?x,y∈X,滿足

(Rb1)d(x,y)=0當(dāng)且僅當(dāng)x=y;

(Rb2)d(x,y)=d(y,x);

(Rb3)d(x,y)≤s[d(x,u)+d(u,v)+d(v,y)],其中u,v∈X{x,y},同時(shí)u/=v.則稱(X,d)為矩形b-度量空間,且s≥1為矩形b-度量空間(X,d)的系數(shù).

注1.1[13]每個(gè)度量空間都是矩形b-度量空間,每個(gè)矩形度量空間也為矩形b-度量空間(這時(shí)s=1).反之不一定成立.

定義1.2[13]設(shè){xn}是矩形b-度量空間(X,d)中的序列.{xn}稱為X 中的Cauchy列,如果

定義1.3[13]設(shè){xn}是矩形b-度量空間(X,d)中的序列.{xn}稱為X 中的收斂列,如果

定義1.4[13]矩形b-度量空間(X,d)稱為完備的,如果X 中的每一Cauchy列都收斂于X中的某個(gè)點(diǎn).

注1.2[13]矩形b-度量空間(X,d)中的數(shù)列的極限點(diǎn)不一定唯一,且收斂列不一定是Cauchy列.

定義1.5[14]稱(x,y)∈X×X是映象F:X×X→X的耦合不動(dòng)點(diǎn),如果F(x,y)=x,F(y,x)=y.

定義1.6[15]稱(gx,gy)∈X×X是映象對(duì)F:X×X→X和g:X→X的重合耦合點(diǎn),如果F(x,y)=gx,F(y,x)=gy.這時(shí),稱(x,y)∈X×X 是映象對(duì)F:X×X→X 和g:X→X的耦合重合點(diǎn).

定義1.7[15]稱(x,y)∈X×X是映象對(duì)F:X×X→X和g:X→X的公共耦合不動(dòng)點(diǎn),如果F(x,y)=gx=x,F(y,x)=gy=y.

定義1.8[16]設(shè)X為一非空集.映象對(duì)F:X×X→X和g:X→X稱為ω-相容的,如果當(dāng)F(x,y)=gx且F(y,x)=gy,總有g(shù)F(x,y)=F(gx,gy).

定義1.9[17]設(shè)X是一非空集,是定義在X中的一偏序關(guān)系,函數(shù)T:X×X→X,g:X→X.T稱為具有混合g-單調(diào)性質(zhì),如果T(x,y)關(guān)于x是g-單調(diào)不減的,關(guān)于y是g-單調(diào)不增的,即對(duì)任意的x,y∈X,有

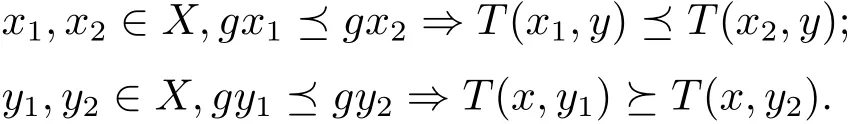
2　主要結(jié)果

為方便起見,下文中出現(xiàn)的函數(shù)ψ和φ均指滿足以下條件的函數(shù)[19]:

(1)ψ:[0,∞)→[0,∞)滿足:1)ψ是非減的且關(guān)于每個(gè)變?cè)沁B續(xù)的;2)ψ(t)=0當(dāng)且僅當(dāng)t=0.

(2)φ:[0,∞)→[0,∞)滿足:1)φ是下半連續(xù)的;2)φ(t)=0?t=0.

定理2.1設(shè)(X,d)是一個(gè)矩形b-度量空間,其系數(shù)s＞1,是定義在X上的一偏序.g:X→X為X上的自映象.映象T:X×X→X具有混合g-單調(diào)性.且滿足以下條件

(1)T(X×X)?g(X);

(2)?(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);

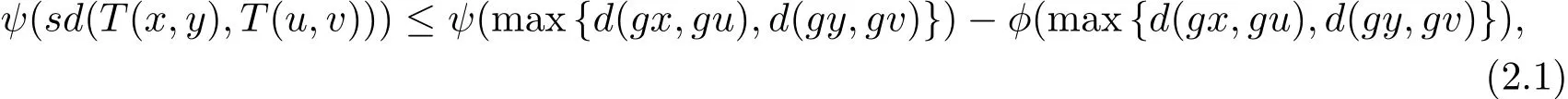
如果g(X)是(X,d)的完備子集,則g和T在X 中有重合耦合點(diǎn).

證根據(jù)條件(2)可得,存在(x0,y0)∈X×X,使得gx0T(x0,y0),gy0T(y0,x0),由于T(X×X)?g(X),所以存在x1,y1∈X,使得gx1=T(x0,y0),gy1=T(y0,x0).類似的,存在x2,y2∈X,使得gx2=T(x1,y1),gy2=T(y1,x1).由于gx0T(x0,y0),gy0T(y0,x0),可得到gx0gx1,gy0gy1.由于映象T具有混合g-單調(diào)性,所以有依此類推,就可得到X 中的兩個(gè)序列{xn}和{yn},使得gxn=T(xn,yn),gyn=T(yn,xn),并且{gxn}和{gyn}還滿足

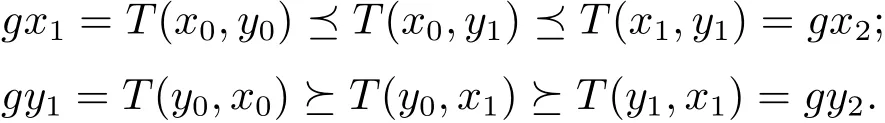
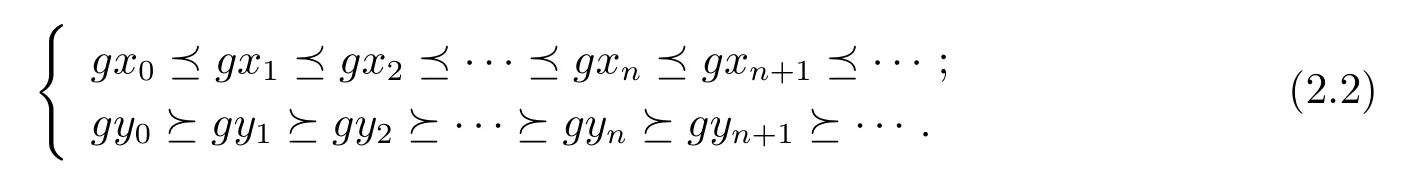
在式(2.1)中,取(x,y)=(xn,yn)和(u,v)=(xn+1,yn+1),并使用式(2.2)可得

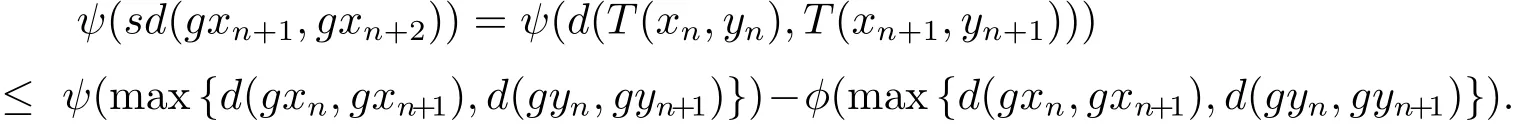
即

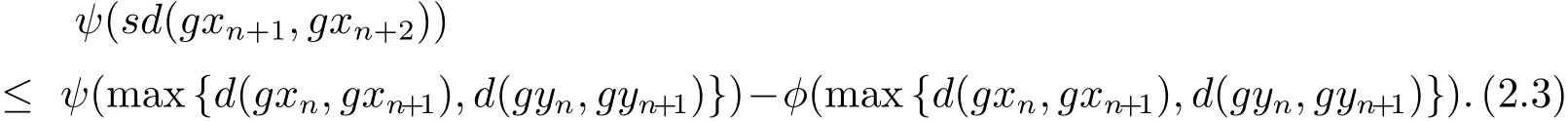
同理可得

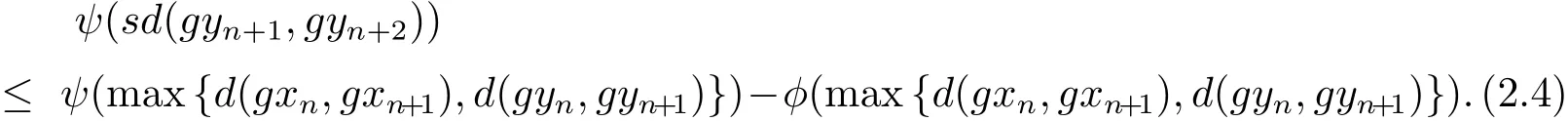
令

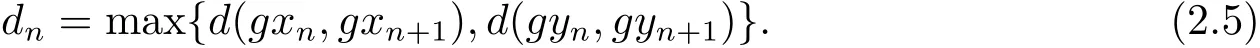
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),進(jìn)而有

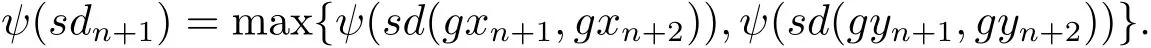
再根據(jù)(2.3),(2.4),(2.5)式和上式可得

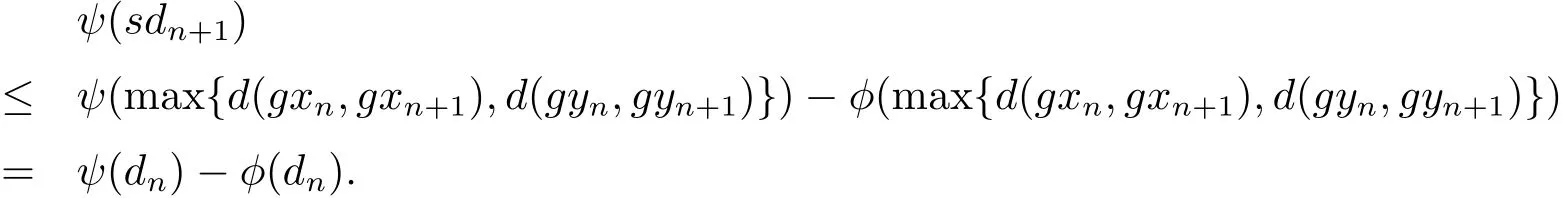
又由函數(shù)φ:[0,∞)→[0,∞),因此由上式可得

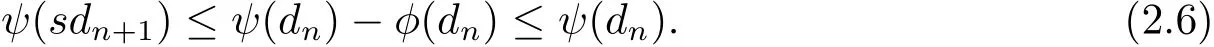
由ψ是非減的,可得

從而可知{dn}單調(diào)遞減的非負(fù)實(shí)數(shù)列,因此存在r∈[0,∞),使得式(2.6)兩邊令n→∞ 時(shí),取極限得ψ(sr)≤ψ(r)?φ(r)≤ψ(r).由ψ是非減的,可得sr≤r.又由s＞1,所有當(dāng)r＞0時(shí),出現(xiàn)矛盾,進(jìn)而可得r=0.于是有由式(2.5)可知

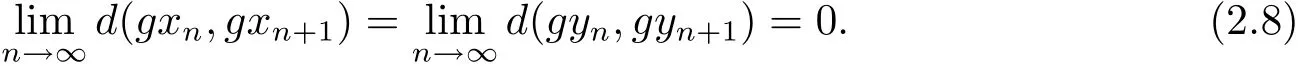
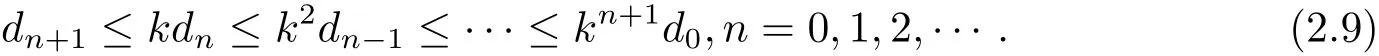
根據(jù)式(2.2),在式(2.1)中取(x,y)=(xn,yn)和(u,v)=(xn+2,yn+2),可得

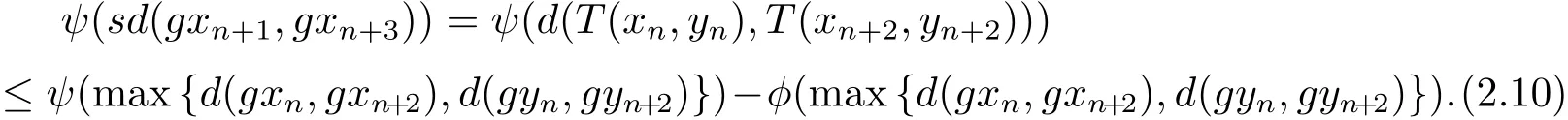
即

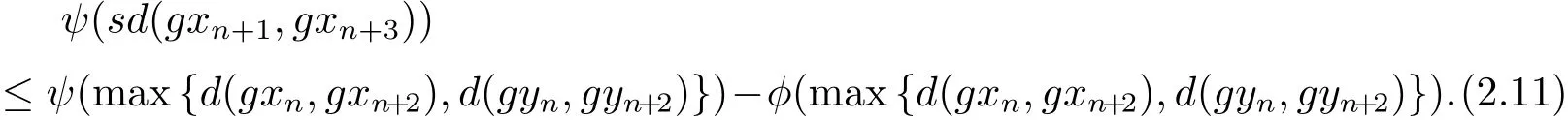
同理可得

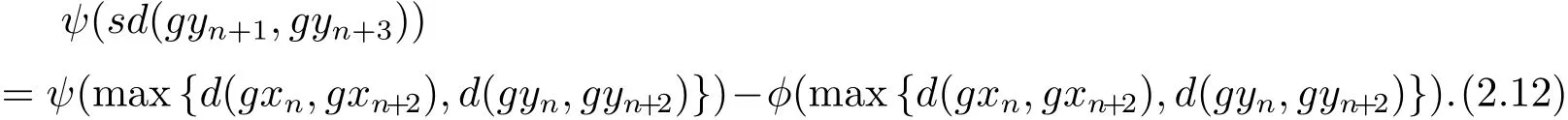
令

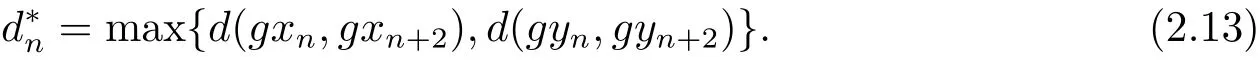
由于max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),進(jìn)而有

再根據(jù) (2.11),(2.12) 和 (2.13) 式可得又由 ψ 是非減的可知又由可知依次類推可得到

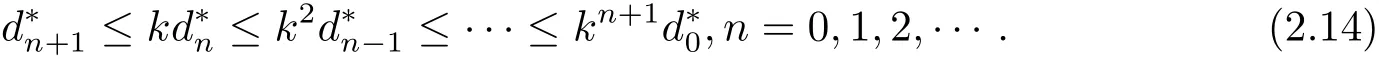
接下來(lái),將證明{gxn}和{gyn}都是gX 中的Cauchy列.

a)當(dāng)p是奇數(shù)時(shí),設(shè)p=2m+1.

事實(shí)上,由性質(zhì)(Rb3)可得

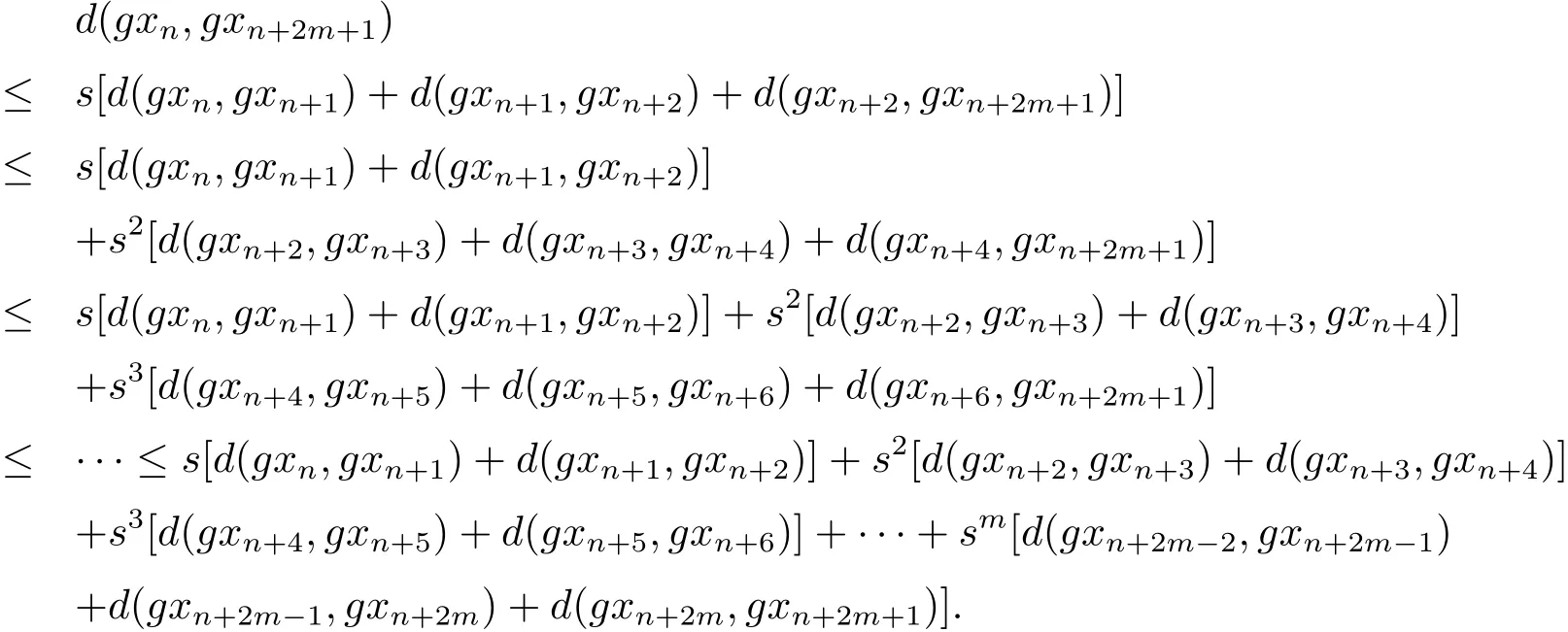
上式即

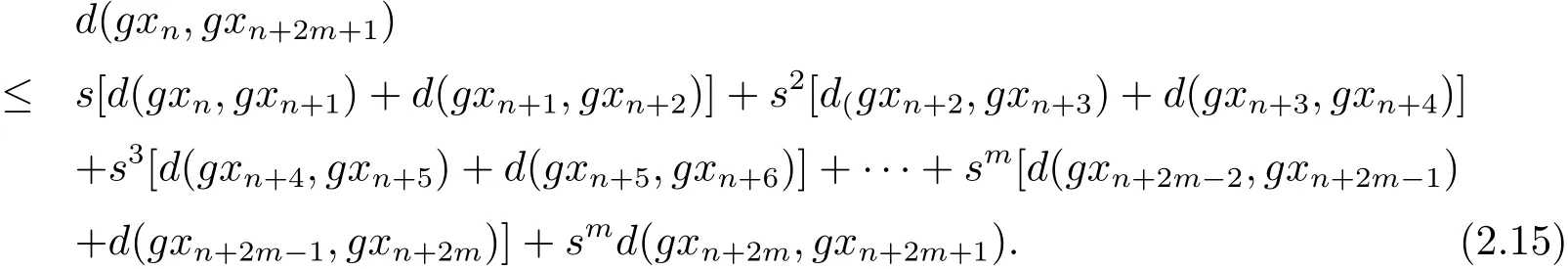
同樣道理可知

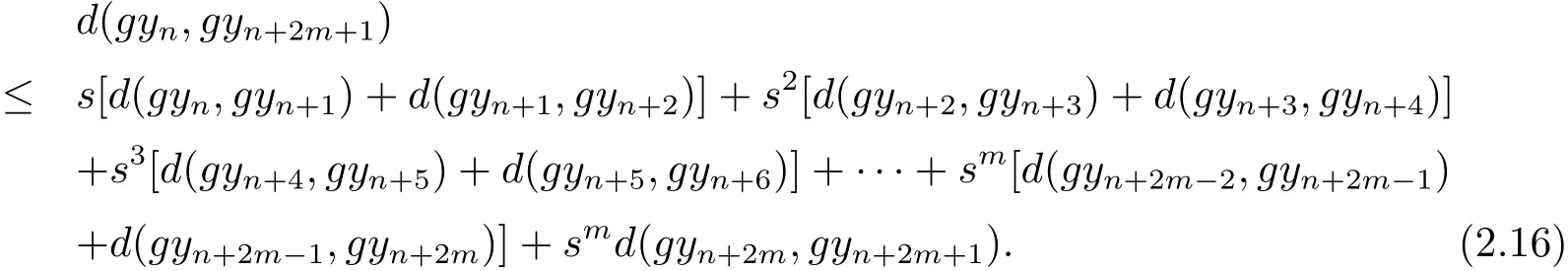
即

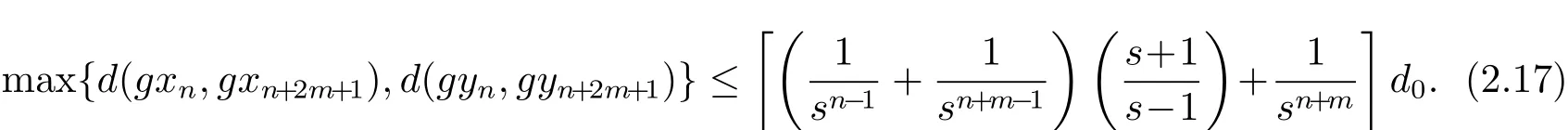
b)當(dāng)p是偶數(shù)時(shí),設(shè)p=2m.使用性質(zhì)(Rb3)可得

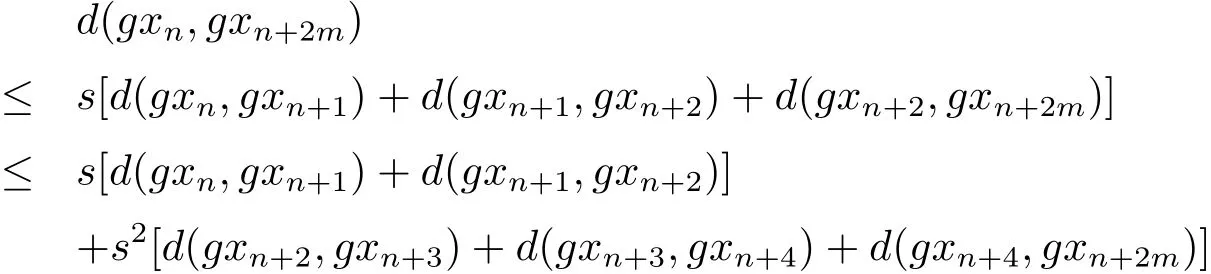
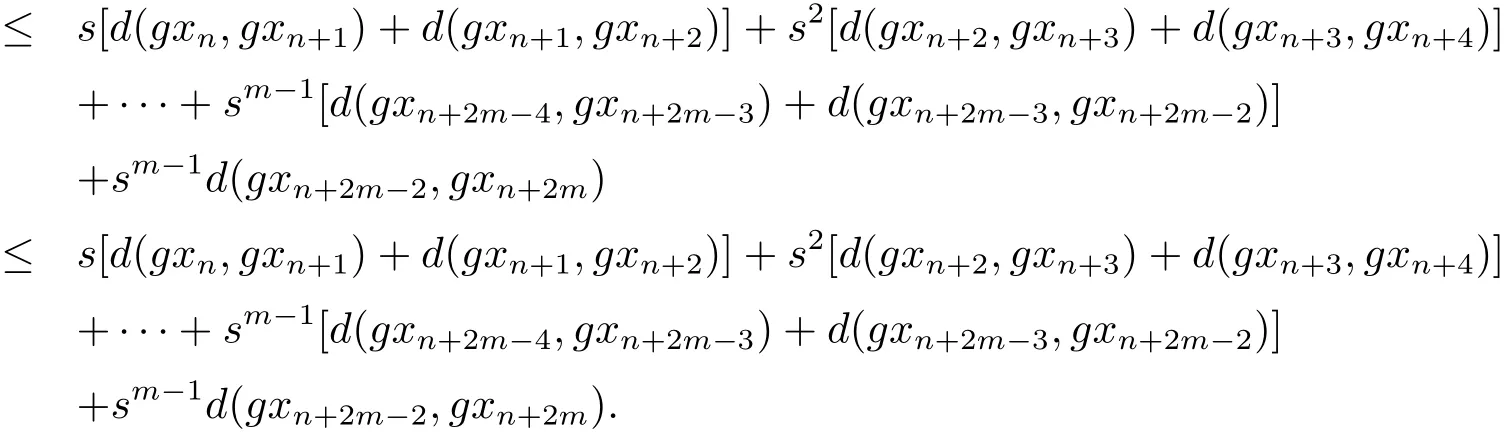
即

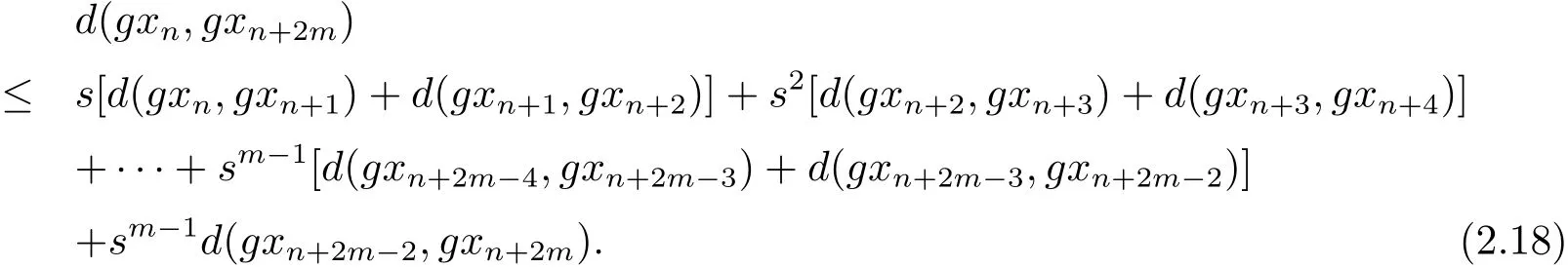
同樣道理可知

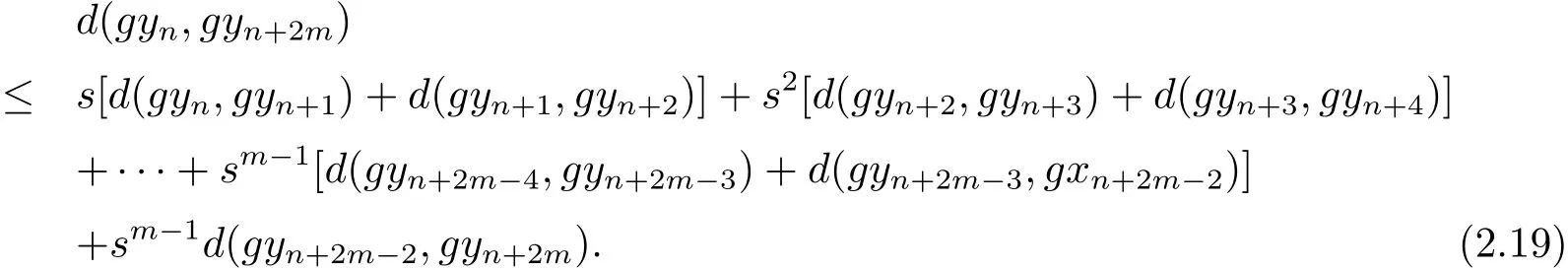
結(jié)合式(2.9),(2.14),(2.18)和(2.19)式,又由可得

進(jìn)而可知

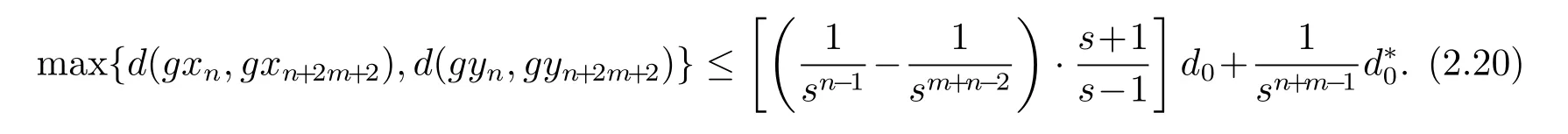
由(2.17)和(2.20)式可得

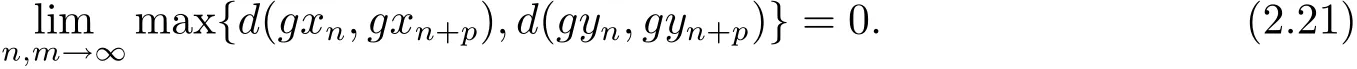
從(2.21)式可知{gxn}和{gyn}是g(X)中的Cauchy列.

又因?yàn)間(X)在是矩形b-度量空間(X,d)的完備子集,所以存在x,y∈X,使得

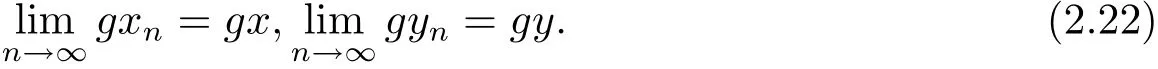
又由(2.1)式可得

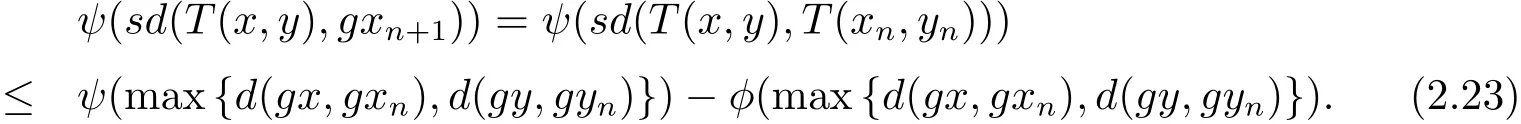
使用三角不等式

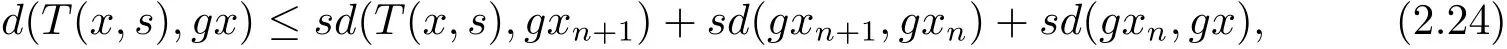
在(2.24)式中,令n→∞取極限,

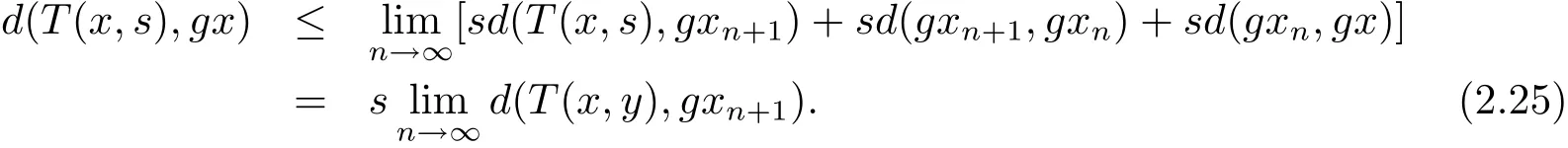
使用(2.22)和(2.25)式,在(2.23)式兩邊令n→∞取極限,可得

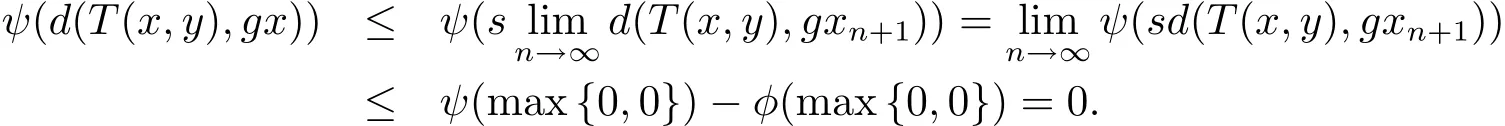
即d(T(x,y),gx)=0,進(jìn)而可知T(x,y)=gx.同理可得T(y,x)=gy.從而有(gx,gy)是g和T的重合耦合點(diǎn),證畢.

定理2.2設(shè)(X,d)是矩形b-度量空間,其系數(shù)s＞1,是定義在X 上的一個(gè)偏序.g:X→X為X上的自映象.映象T:X×X→X具有混合g-單調(diào)性.且滿足以下條件

(1)T(X×X)?g(X);

(2)?(x0,y0)∈X×X 使得gx0T(x0,y0),gy0T(y0,x0);

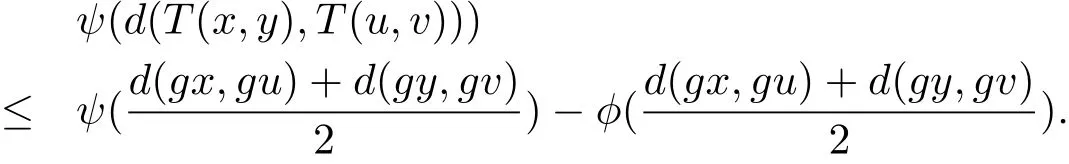
如果g(X)是(X,d)中的完備集,則g和T在X 中有重合耦合點(diǎn).

證與定理2.1證明方法相同,略去.

注2.1令定理2.1中的自映象g為恒等映象I,即有下面推論.

推論2.1設(shè)(X,d)是矩形b-度量空間,其系數(shù)s＞1,是定義在X 上的一個(gè)偏序.映象T:X×X→X.如果滿足以下條件

(1)?(x0,y0)∈X×X 使得x0T(x0,y0),y0T(y0,x0);

則T在X中有耦合不動(dòng)點(diǎn).

注2.2?a,b,c∈[0,+∞),有

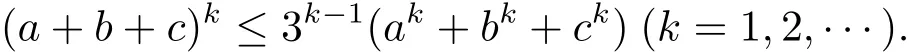
證顯然當(dāng)k=1,2時(shí)結(jié)論成立,假設(shè)當(dāng)k=m時(shí)結(jié)論成立,即

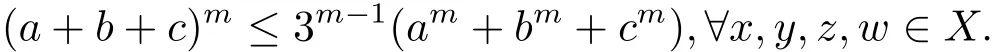
現(xiàn)證當(dāng)k=m+1時(shí)結(jié)論也成立.事實(shí)上,有

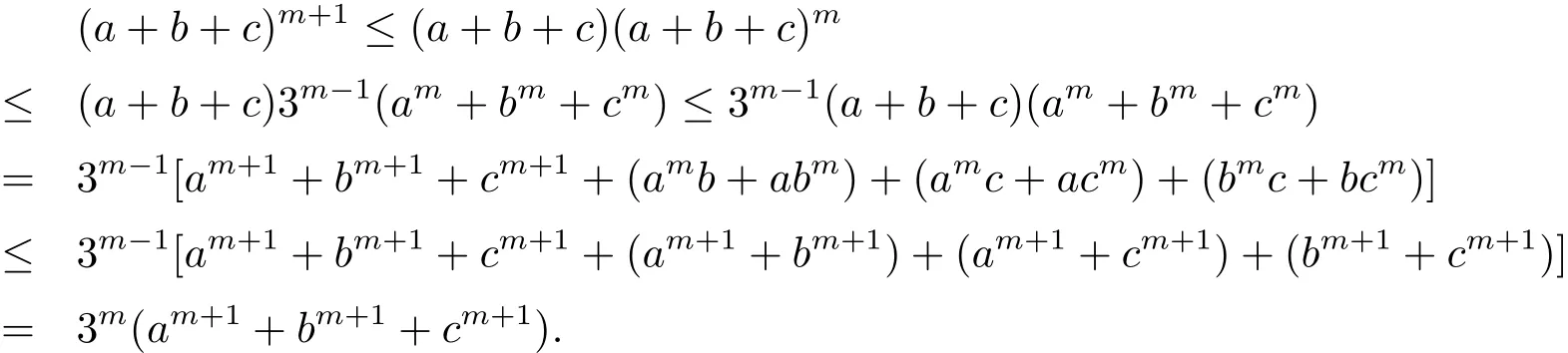
從而結(jié)論對(duì)一切自然數(shù)k成立.

例2.1設(shè)X=R,?x,y∈X,定義d(x,y)=(x?y)2,則(X,d)是一個(gè)系數(shù)s=3的矩形b-度量空間.設(shè)X上的偏序關(guān)系定義如下:xy?x≤y.定義函數(shù)T:X×X→R+和g:X→R+分別如下

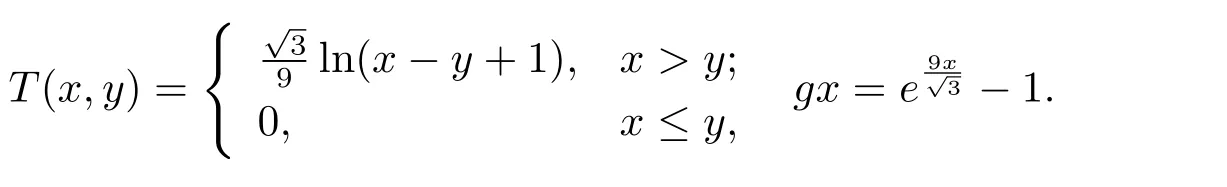
易得T(X×X)?g(X),且T具有g(shù)-混合單調(diào)性.當(dāng)

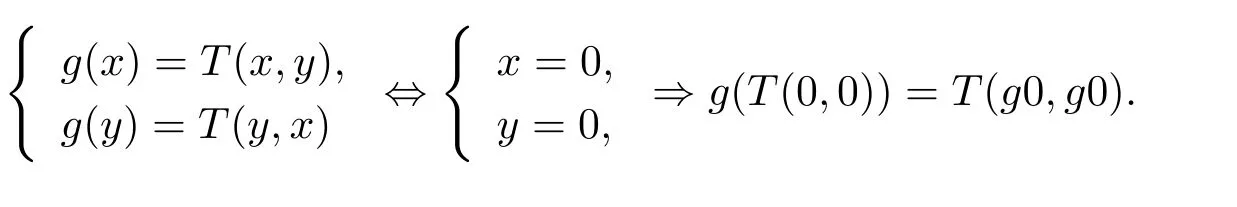
即F和g是ω-相容的.令(x,y)=(0,0)時(shí),這時(shí)有g(shù)0T(0,0),g0T(0,0).

定義函數(shù)ψ,φ:R+→R+分別為

下面分四種情況討論.

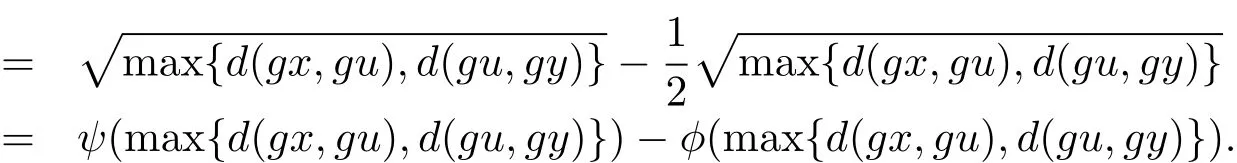
4)當(dāng)T(x,y)=0,T(u,v)=0時(shí),即x≤y,u≤v時(shí),顯然成立.

從而根據(jù)定理2.1,可證得T和g具有耦合重合點(diǎn),且T(0,0)=g0=0.

3　不動(dòng)點(diǎn)的唯一性

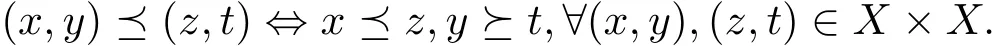
定理3.1在定理2.1的條件下,假設(shè)g和T是ω-相容的,且g和T的任意兩個(gè)重合耦合點(diǎn)(gx?,gy?)和(gz?,gt?)都有相應(yīng)的公共可比較點(diǎn)(gu?,gv?)∈ X ×X,這時(shí)g和T 有唯一的耦合公共不動(dòng)點(diǎn).

證由定理2.1可知g和T至少存在一個(gè)重合耦合點(diǎn).不妨假設(shè)(x,y),(z,t)∈X×X是g和T的任意兩個(gè)耦合重合點(diǎn),即T(x,y)=gx,T(y,x)=gy和T(z,t)=gz,T(t,z)=gt.現(xiàn)證(gx,gy)=(gz,gt).

由已知條件可知,存在(u,v)∈X×X,使得(gu,gv)分別和(gx,gy),(gz,gt)都可比較.

a)當(dāng)可比較關(guān)系為

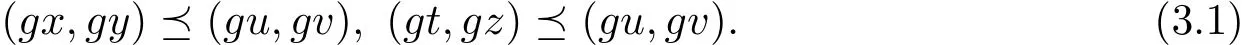
令

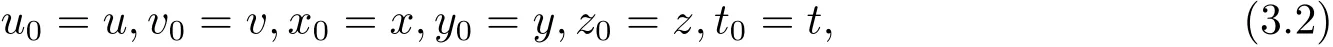
則?(u1,v1)∈X×X,使得

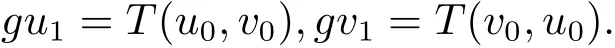
依次類推,會(huì)得到兩個(gè)數(shù)列{gun}和{gvn}分別為

同樣道理,可以得到數(shù)列{gxn},{gyn}和{gzn},{gtn}分別為

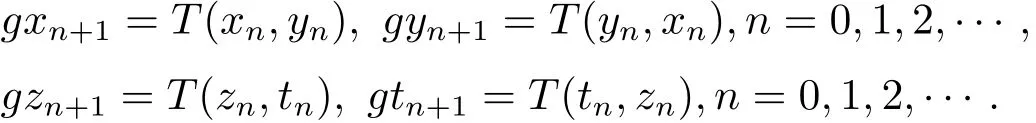
由于(x,y)是g,T的耦合重合點(diǎn),則有

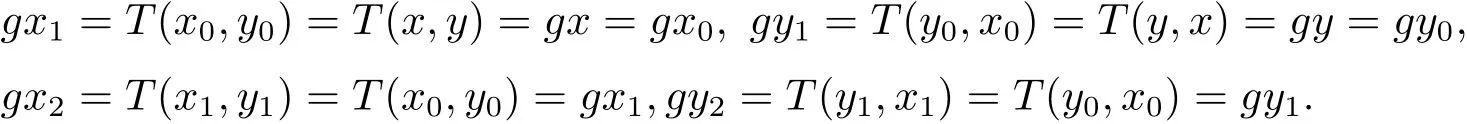
依次類推可知 gx0=gx1= ···=gxn= ···,gy0=gy1= ···=gyn= ···.即

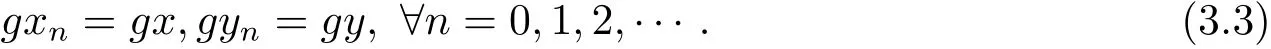
相同道理可知

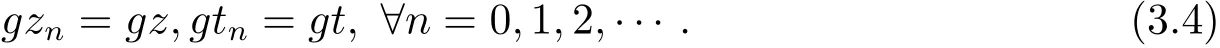
由于(3.1)和(3.2)式可得

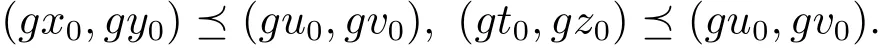
由于T具有混合g-單調(diào)性,所以可得

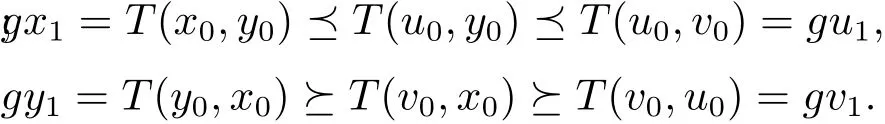
即(gx1,gy1)(gu1,gv1).同理可得(gx2,gy2)(gu2,gv2).這樣繼續(xù)做下去,可得

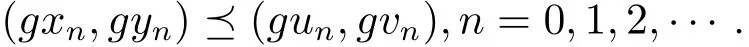
類似方法,可得

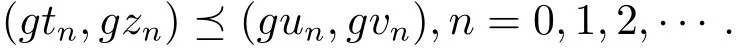
結(jié)合(3.3)和(3.4)式可得

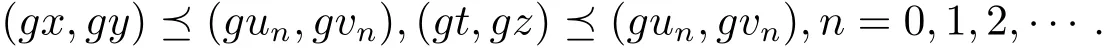
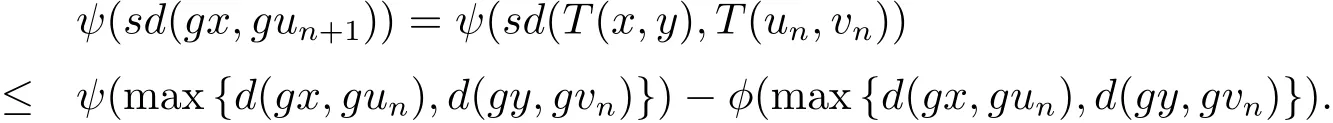
即

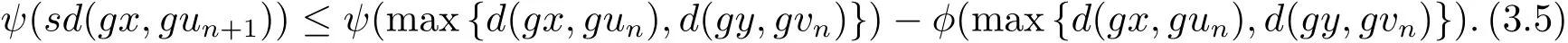
同理可得

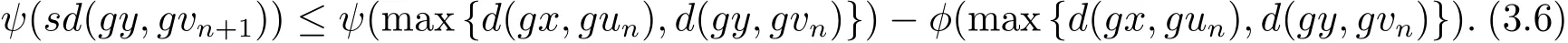
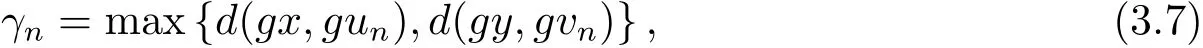
現(xiàn)令聯(lián)立(3.5),(3.6)和(3.7)式,又由max{ψ(a),ψ(b)}= ψ(max{a,b}),?a,b∈ [0,+∞),可得到

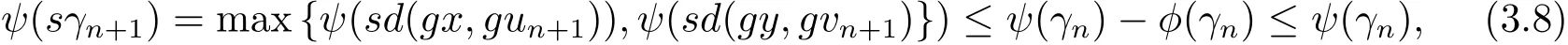
從而可得γn+1≤γn.所以可知{γn}單調(diào)遞減的非負(fù)實(shí)數(shù)列,存在r∈X,使得r≥0且因?yàn)閷⑸鲜絻蛇吜?n → ∞ 時(shí),取極限得ψ(sr)≤ψ(r)?φ(r).當(dāng)r＞0時(shí),出現(xiàn)矛盾.即r=0.于是有

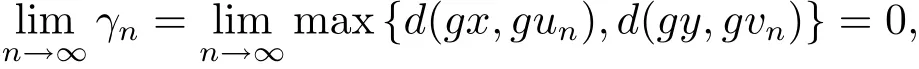
進(jìn)而可知

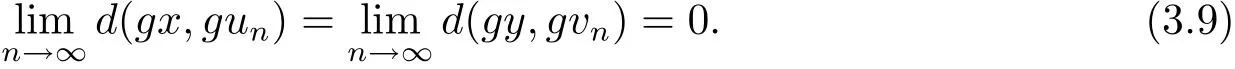
同樣道理可證得

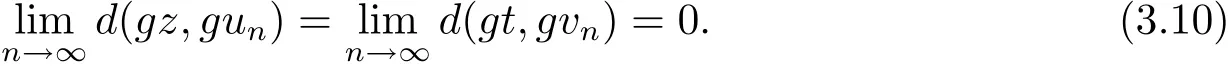
由(3.9)和(3.10)式可得到

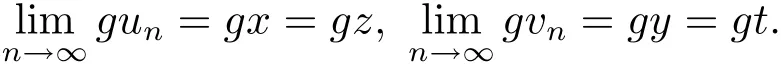
即(gx,gy)=(gz,gt).所以g和T具有唯一的重合耦合點(diǎn).又因?yàn)間和T是ω-相容的,得到

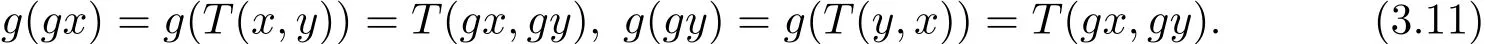
由于?m,n∈X,使得gx=m,gy=n,那么(3.12)式可整理為

因此(m,n)也是g和T的一個(gè)耦合重合點(diǎn),由重合耦合點(diǎn)的唯一性知gm=gx=m,gn=gy=n.又由(3.12)式可得m=gm=T(m,n),n=gn=T(n,m).即證得g和T有耦合公共不動(dòng)點(diǎn).由于g和T的重合耦合點(diǎn)具有唯一性,因此g和T的耦合公共不動(dòng)點(diǎn)也具有唯一性.

同a)的證明方法類似,上述三種情況同樣也能證得g和T的耦合公共不動(dòng)點(diǎn)也具有唯一性.

4　在積分方程中的應(yīng)用

假設(shè)X=C[a,b]是定義在[a,b]上的連續(xù)函數(shù)全體.≤是定義在X 上的偏序關(guān)系,定義

定義d:X×X→R+為

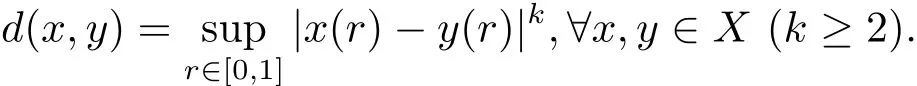
這時(shí)易知(X,d)是一個(gè)完備的矩形b-度量空間,由注2.2可知,其系數(shù)s=3k?1.

考慮以下積分方程組問(wèn)題

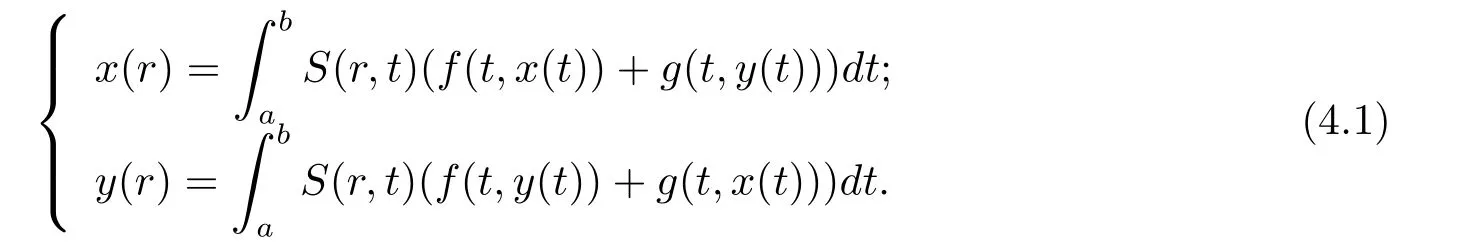
接下來(lái),假設(shè)下面幾個(gè)條件成立.

(i)S(r,t):[a,b]×[a,b]→R+是連續(xù)函數(shù).

(ii)f,g:[a,b]×R→R是連續(xù)函數(shù).

(iii) ?(x0,y0)∈X×X,使得

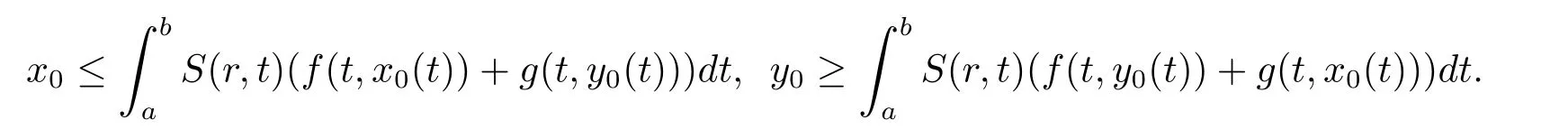
(iv)?μ,ν使得對(duì)于任意的r∈[a,b],x,y∈R,有

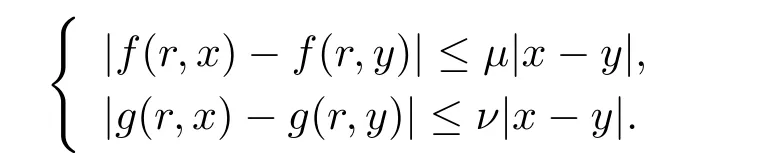
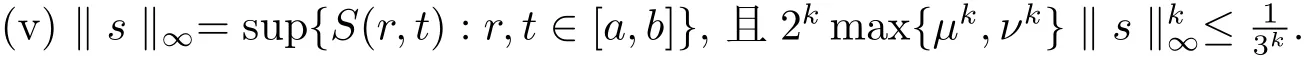
定理4.1由上述條件(i)–(v)成立,則積分方程組(4.1)有唯一的解.

證構(gòu)造函數(shù)T:X×X→X和g:X→X如下

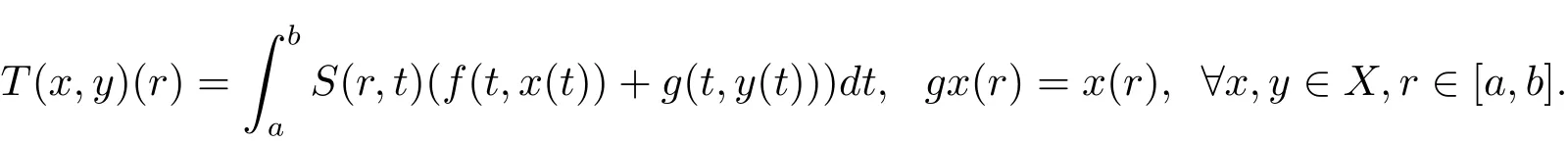
則由條件(iii)可知gx0T(x0,y0),gy0T(y0,x0),且g和T具有ω-相容性.又由條件(iv)和(v)可得

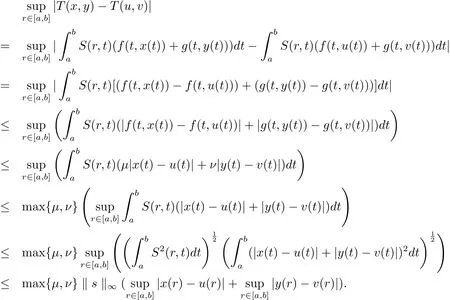
于是由條件(v),上式可整理為

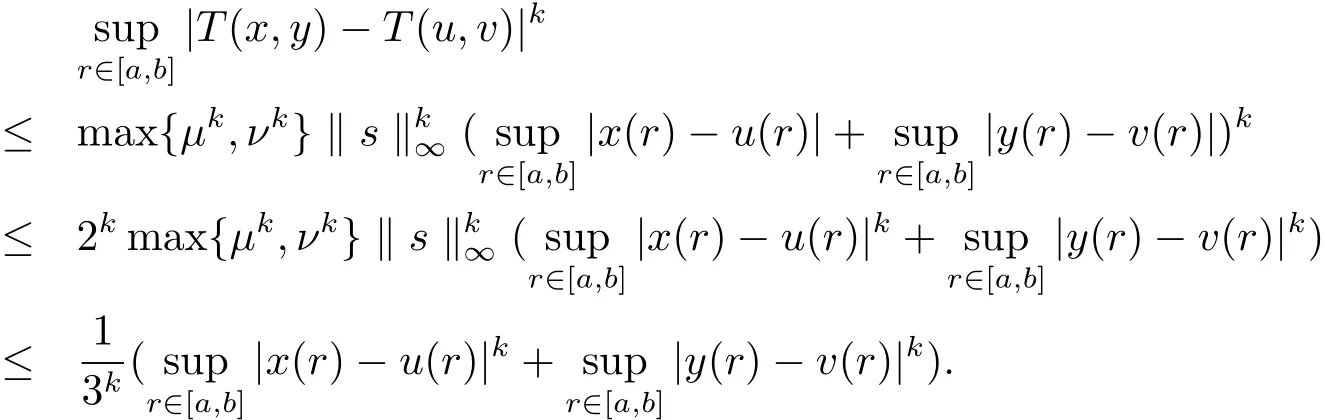
上式即為

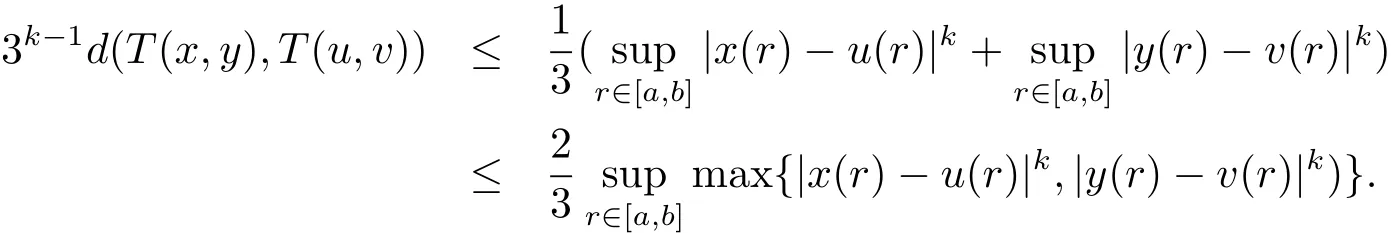
于是

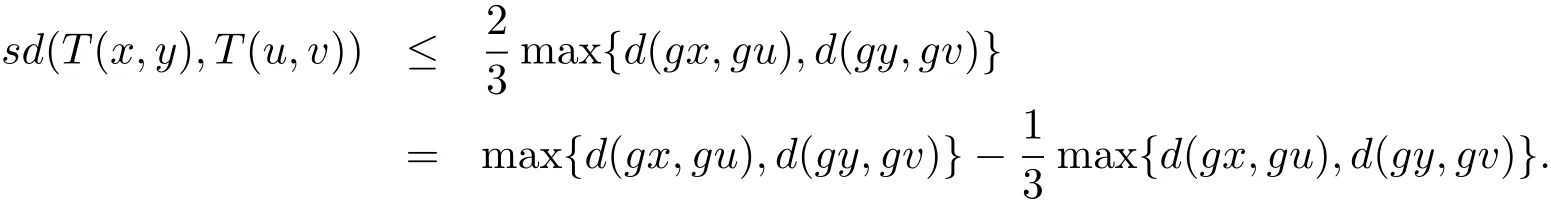
令函數(shù)ψ,φ:R+→R+分別為那么上式即為

ψ(sd(T(x,y),T(u,v)))≤ ψ(max{d(gx,gu),d(gy,gv)})?φ(max{d(gx,gu),d(gy,gv)}).由此易知定理3.1的所有條件被滿足,于是,存在(x?,y?)∈X×x,使得

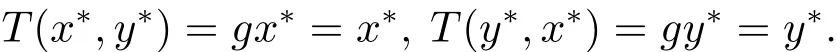
即(x?,y?)也為方程組(4.1)在C[a,b]上的唯一解.

[1]Bakhtin I A.The contraction mapping principle in quasimetric spaces[J].Funct.Anal.,Unianowsk Gos.Ped.Inst.,1989,30:26–37.

[2]Azam A,Arshad M.Kannan fixed point theorems on generalized metric spaces[J].J.Nonl.Sci.Appl.,2008,1:45–48.

[3]Azam A,Arshad M,Beg I.Banach contraction principle on cone rectangular metric spaces[J].Appl.Anal.Disc.Math.,2009,3:236–241.

[4]Chen C M.Common fixed point theorem in complete generalized metric spaces[J].J.Appl.Math.,Article ID 945915,2012.

[5]Das P.A fixed point theorem on a class of generalized metric spaces[J].Korean J.Math.Sci.,2002,9:29–33.

[6]Das P,Dey L K.A fixed point theorem in generalised metric spaces[J].Soochow J.Math.,2007,33(1):33–39.

[7]Lahiri B K.Das,P.Fixed point of a Ljubomir Ciric’s quasi-contraction mapping in a generalized metric space[J].Publ.Math.Debrecen,2002,61(3-4):589–594.

[8]Das P,Lahri B K.Fixed point of contractive mappings in a generalised metric space[J].Math.Slovaca,2009,59(4):499–504.

[9]Erhan I M,Karapinar E,Sekuli′c T.Fixed points of(ψ,φ)contractions on rectangular metric spaces[J].Fixed Point Theory Appl.,2012,138,DOI:10.1186/1687-1812-2012-138.

[10]Lakzian H,Samet B.Fixed points for(ψ,φ)-weakly contractions mapping in generalized metric spaces[J].Appl.Math.Lett.,2012,25(5):902–906.

[12]魏利,周海云.Banach空間中有限個(gè)增生算子公共零點(diǎn)的帶誤差項(xiàng)的迭代格式[J].數(shù)學(xué)雜志,2009,29(3):329–334.

[12]Gu F.Some new common coupled fixed point results in two generalized metric spaces[J].Fixed Point The.Appl.,2013,2013:181,DOI:10.1186/1687-1812-2013-181.

[13]Branciari A.A fixed point theorem of Banach-Caccippoli type on a class of generalized metric spaces[J].Publ.Math.Debrecen,2000,57:31–37.

[14]Bhaskar T G,Lakshmikantham V.Fixed point theorems in partially ordered metric spaces and applications[J].Nonl.Anal.,2006,65:1379–1393.

[15]Lakshmikantham V,′Ciri′c L B.Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces[J].Nonl.Anal.,2009,70:341–4349.

[16]Abbas M,Khan M A,Radenov′?c S.Common coupled fixed point theorem in cone metric space for ω-compatible mappings[J].Appl.Math.Comput.,2010,217:195–202.

[17]Berinde V,Borcut M.Tripled fixed point theorems for contractive type mappings in partially ordered metric spaces[J].Nonl.Anal.,2011,74(15):4889–4897.

[18]谷峰.不動(dòng)點(diǎn)定理與非線性算子迭代序列的收斂性[M].哈爾濱:黑龍江科技出版社,2002.