延期支付與訂購量相關的易腐產品庫存決策模型

韋才敏,李忠萍,林小蘋

(1.汕頭大學理學院,廣東汕頭 515063)

(2.汕頭大學數字信號與圖像處理技術重點實驗室,廣東汕頭 515063)

1　引言

當供應鏈成員企業面臨資金約束,而銀行信貸緊縮、資本市場不發達,企業如何從成員企業間獲得內部融資來實現最優的運營決策是供應鏈融資管理研究的熱點問題[1].內部融資包括提前付款融資模式與延期支付融資模式.針對延期支付而言,其形式有兩種:在供應商為強勢企業的情況下,供應商為了激勵零售商的購買行為,往往會給予零售商一些優惠策略[2];在零售商為強勢企業的情況下,其通過占用上游企業供應商的資金,擴大市場規模來獲得收益[1].

已有很多國內外學者對有關延期支付的問題進行研究,如Goyal[3]最早構建了允許延期支付的EOQ模型,隨后又有不少科研工作者對該模型進行擴展.在允許延期支付條件下,Chung[4]發現了一個確定EOQ下的定理.在兩階段的信貸策略下,基于EPQ模型框架,Huang[5]獲得了零售商的最優補貨決策.在供應商提供的延期支付與零售商訂購量相關時,Chen[6]等人建立了零售商的EOQ模型,獲得了最優訂購量及訂購周期.基于EPQ模型框架,針對變質產品,在零售商提前還款及供應商給予其現金折扣優惠策略下,李明芳[7]等人建立了零售商的庫存決策模型,獲得了限制條件下零售商的最優決策,然而,其是對變質很低的情形下的結果,在實際應用中有一定的限制.

然而,上述的研究都假定需求率是確定的常數,而實際中需求往往和零售價格相關,此種情況下的延期支付問題,也有學者對其進行研究.在數量折扣與延期支付固定的條件下,Sana[8]等人考慮了需求依賴于庫存水平、時間及價格等背景下,其獲得了零售商的最優決策解.針對隨機需求情形,在兩水平的信貸策略下,Dye[9]等人建立了確定的EOQ模型,通過粒子群優化算法獲得了最優零售價格、補貨數及補貨策略.針對需求依賴于價格的情形,李明芳[10]等人在供應商允許延期支付和現金折扣的優惠策略下,建立了聯合庫決策模型,獲得了零售商的最優訂購周期、最優零售價格及最優付款時間.梁培培[11]等人建立了需求基于瞬時庫存的延期支付庫存決策模型,并驗證了協調的必然性.基于延期支付,Shukla[12]等人建立了需求依賴于時間的EOQ模型,獲得了零售商最優訂購策略.Shukla[13]等人建立了需求依賴于庫存水平的EOQ模型,獲得了最優訂購周期、訂購量,實現了相關成本的最小化.

在以上文獻中,雖然考慮了需求率和零售價格、時間、庫存水平等相關下的延期支付庫存決策問題,但大多在不允許缺貨假設下進行的,且很少考慮延期支付與訂購量相關情形下的庫存決策模型.為了使模型更接近實際情況,在以上的文獻基礎之上,針對單周期內市場的需求依賴于零售價格、允許缺貨發生的情形,建立了延期支付與訂購量相關的易腐產品的庫存決策模型.討論了如何制定最優缺貨時間、訂購周期及零售價格,來實現零售商年利潤最大化,并給出了求解該最優決策問題的內點算法,為零售商在庫存管理方面提供了理論支持.并通過數值實驗分析參數對最優決策的影響.

2　符號與假設

2.1　符號

模型中所使用的符號如表1所示.

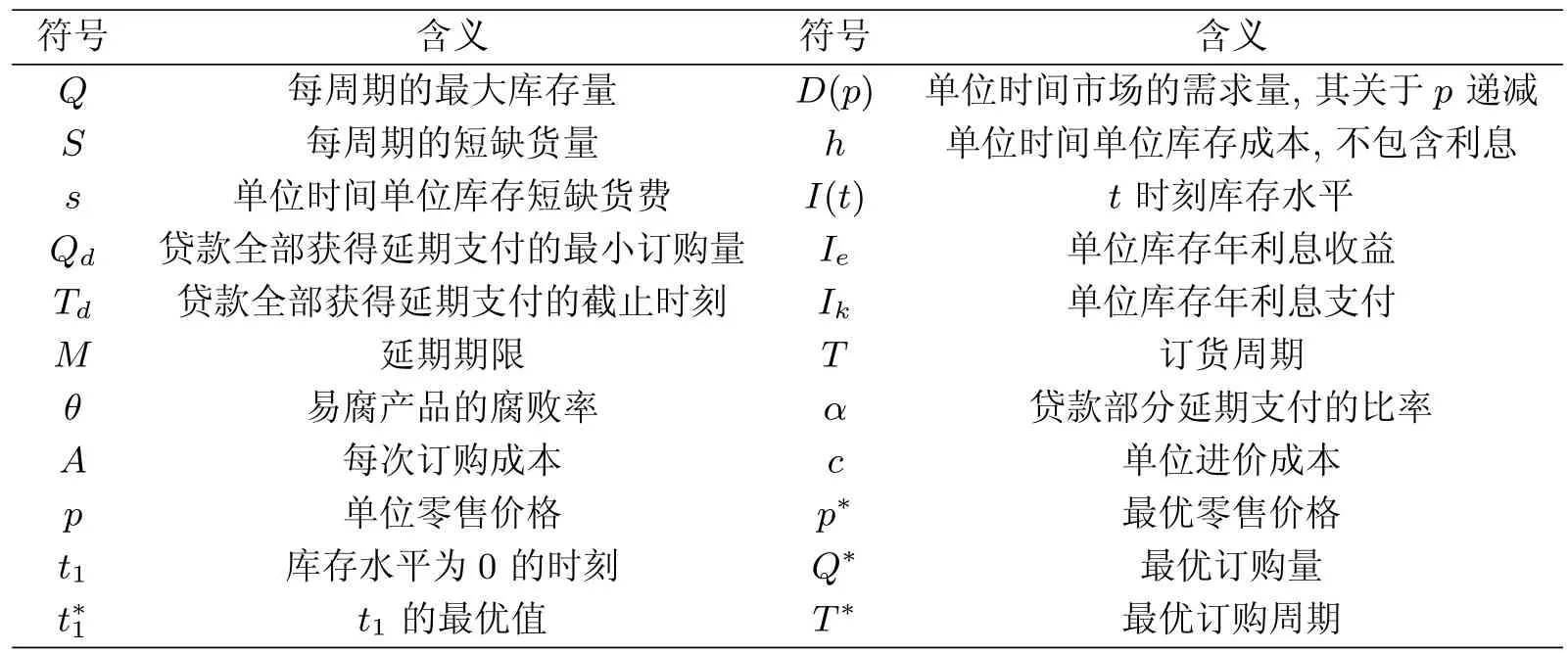
表1:符號說明

2.2　假設

在模型的構建中所做的假設如下:

(1)時間期限無限;

(2)交貨時間忽略不計;

(3)允許缺貨發生,且缺貨量完全延期供給;

(4)僅考慮單一易腐產品,如食品、水果、蔬菜等;

(5)單位時間市場的需求量D(p)=a?bp,其中a為市場的潛在需求量,b＞0為客戶對價格的敏感度;

(6)如果零售商的訂購量Q+S≥Qd(Td≤t1),貸款全部獲得延期支付,即零售商允許在延期期限M 償還進貨費用c(Q+S);如果零售商的訂購量Q+S＜Qd(Td＞t1),貸款部分延期支付,可以延期到期限M 的費用為αc(Q+S),其余費用在訂購產品時立即付清;

(7)在延期期限M 之前零售商將銷售收入存入銀行獲得利息收益,在延期期限M 之后如果零售商不償還貸款,供應商將向其收取利息,且Ik＞Ie.

3　數學模型

本節首先獲得t時刻零售商庫存水平的表達式I(t),然后分情況討論零售商單位時間的平均總利潤表達式.類似[14],I(t)滿足以下微分方程

滿足條件I(t1)=0,可得微分方程的解為

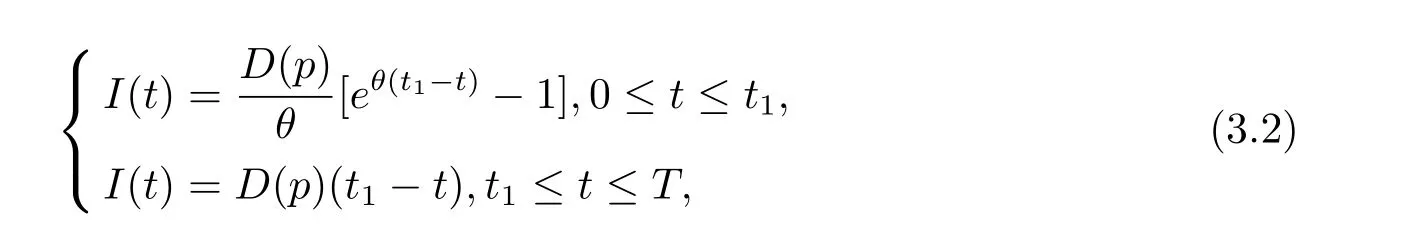
且滿足

由(3.2)與(3.3)式,可得訂購周期內零售商庫存水平隨時間變化的大致圖形如下.

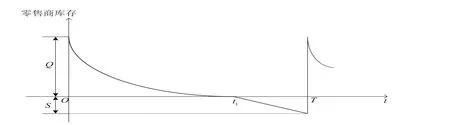
圖1:零售商庫存水平變化圖

零售商單位時間的平均總利潤為ATP=ATP(t1,T,p)=(銷售收入?總費用)/訂購周期.總費用=訂購費用+庫存費用+腐敗損失費用+采購費用+短缺費用+利息收入?利息支出.在一個周期內總銷售收入為pD(p)T,訂購費用為A,庫存費用為腐敗損失費用為c[Q?D(p)t1],采購費用為c(Q+S),短缺費用為其中在貸款延期到達之前零售商將銷售產品所獲得的收益存入銀行獲得利息收入,而在延期期限到達之后如果零售商不償還貸款,則其需要支付高額利息費用,而對于訂購周期內利息收入與利息支出,根據貸款全部或部分延期支付分為以下兩種情形.

情形1Td≤t1.

情形2 Td＞t1.

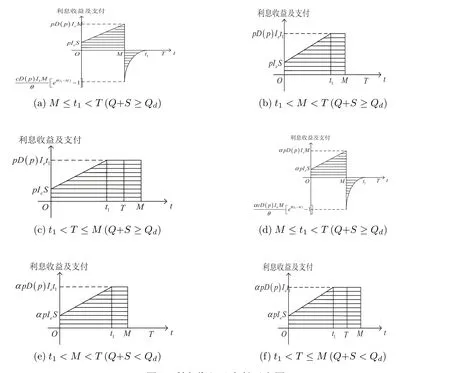
圖2:利息收入及支付示意圖

綜合情形1與情形2,可得零售商單位時間的平均總利潤為

其中

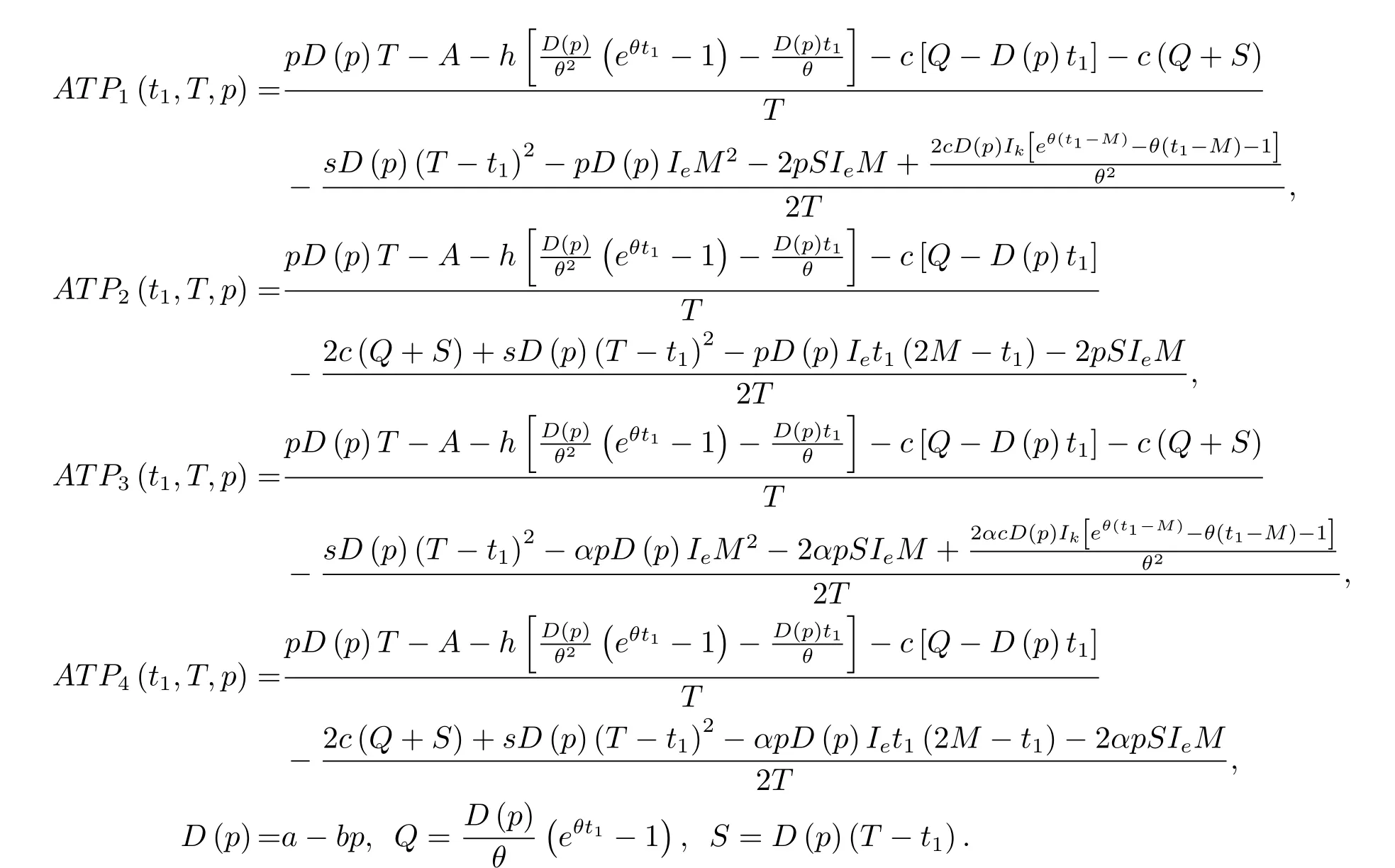
4　最優決策分析

本節針對延期支付與訂購量相關的易腐產品庫存決策模型,且允許缺貨發生,缺貨完全延期供給.以零售商單位時間內的平均總利潤最大化為目標,獲得最優零售價格、最優訂購周期及最優缺貨時間即最優化問題為以下形式

由于(4.1)式是含有約束條件的非線性優化問題,由于計算的復雜性,因此,很難求得該問題的解析解.接下來,在限制一些條件情況下,獲得該問題的解析解;然后,又提出一種算法來獲取該問題最優數值解.

4.1　易腐率很小時的最優決策

首先,通過一個定理來說明優化問題(4.1)的最優解的存在性.然后,當產品易腐率很低時,運用泰勒展開式定理,在固定T時獲得最優零售價格及最優缺貨時間表達式,實現了零售商單位時間的平均總利潤最大化.

接下來,通過一個定理來說明優化問題(4.1)的最優解的存在性.

定理4.1存在最優零售價格、最優訂購周期及最優缺貨時間使得ATPi(t1,T,p)達到最大化.

證由于決策目標函數ATPi(t1,T,p)對應的海塞矩陣為可以判定其對角線元素H11,H22,H33均小于零,即證.其中

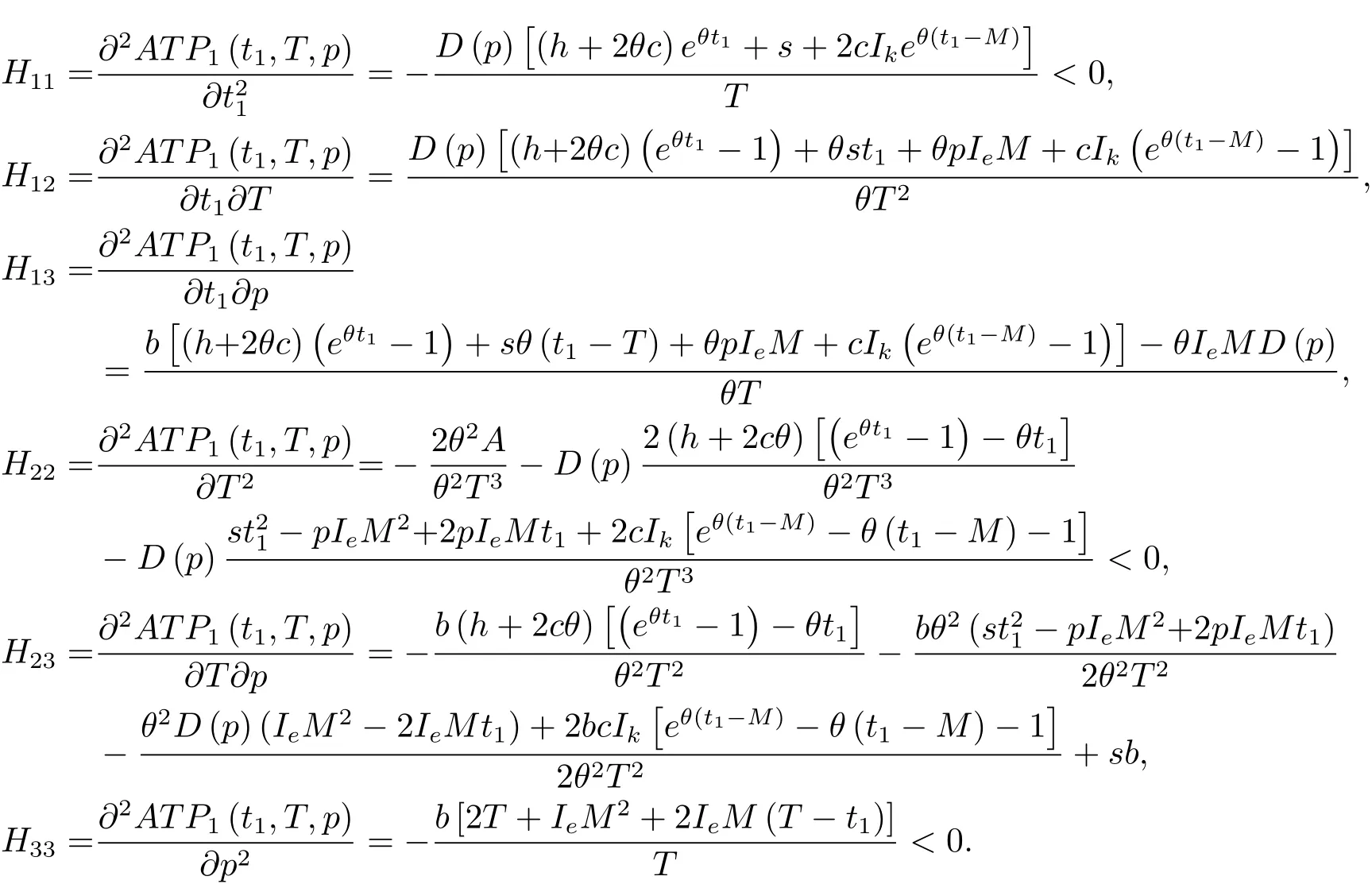
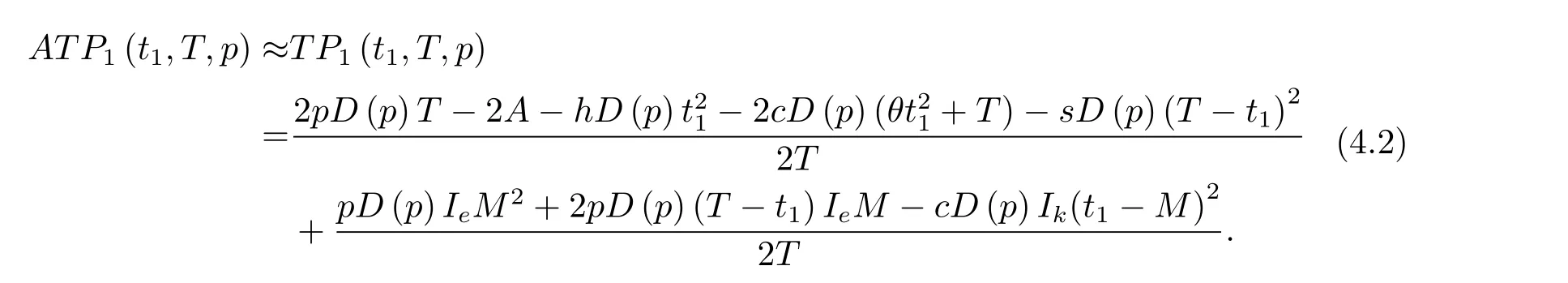
然后,在產品易腐率很低及固定T的情況下,通過一個定理給出訂購周期內零售商的最優零售價格及最優缺貨時間的解析解,并實現了零售商單位時間的平均總利潤的最大化.

定理4.2當T固定,且B2?4AC≥0時,存在最優零售價格及最優缺貨時間使得零售商單位時間的平均總利潤ATPi(t1,T,p)達到最大化,且

其中

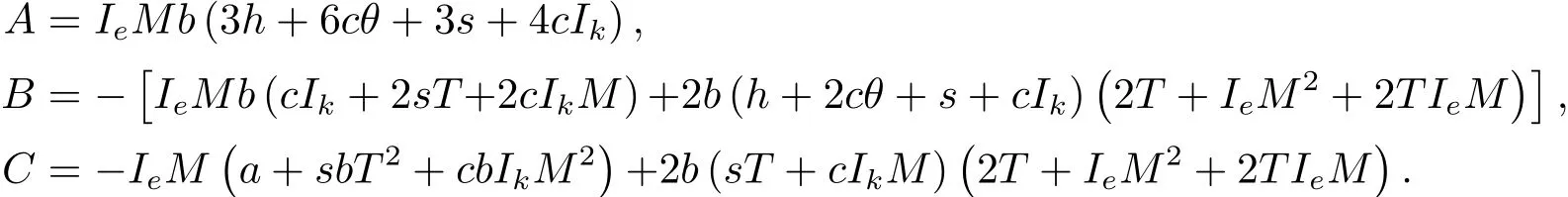
證在固定T的情況下,決策函數TPi(t1,T,p)關于t1,p求一階偏導數,可得

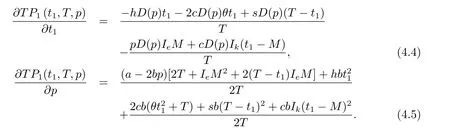
令(4.4)與(4.5)式等于零,可得

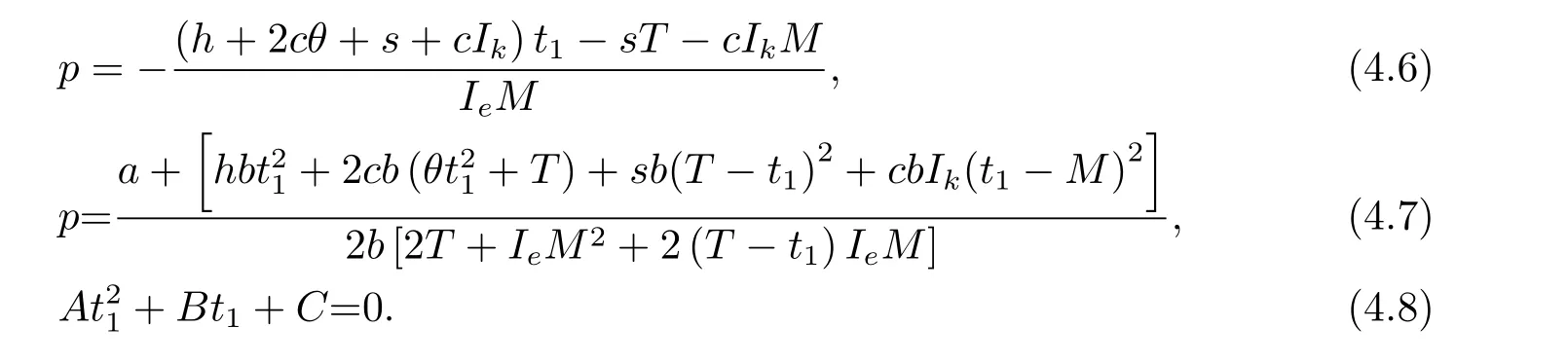
由(4.8)與(4.6)式,可得(4.3)式,對應的海塞矩陣為

4.2　易腐率比較大時的最優決策

令x=(p,T,t1),則方程(3.4)中的目標函數可轉化為

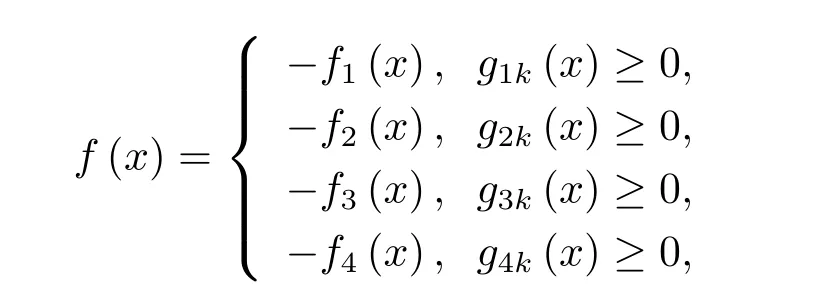
其中 gik≥ 0(i=1,···,4;k=1,···,4)為不等式約束條件;fi(x)= ?ATPi(t1,T,p),則公式(3.4)可變為

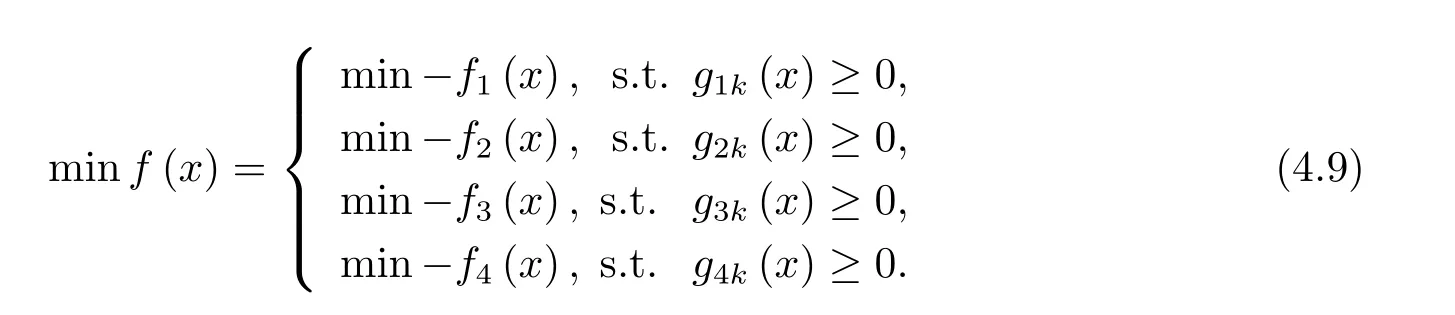
通過minf(x)構造罰函數,即增廣目標函數的無約束子問題為

為了獲得優化問題(4.9)的數值解,本節采用內點算法[15?17]進行計算,該算法的具體迭代流程圖如下.

圖3:算法流程圖

注4.1以上算法中,罰因子選擇準則為選取數列{τk},滿足以下條件

(1)正數列;

(2)單調遞減趨于零.

注4.2罰因子的選擇對該算法有一定的影響,一般來說不能太大也不能太小,當罰因子過大,可能會使問題(4.10)遠離問題(4.9);當罰因子過小,即τk→0,懲罰項→0·∞形式,則會給增廣目標函數的求解帶來計算上的困難.

假設某物品的周需求量為D=100000?5000p千克,每千克該物品的購買成本為c=3元,每次固定訂購費用為A=1000元,每周期每千克該物品的存儲費用為h=0.3元,每周期每千克該物品的存儲費用為s=2元,該物品的變質率為θ=0.01,延期期限為M=0.5周,年利息收益率為Ie=0.09,年利息支付率為Ie=0.13,貸款部分延期支付的比率α=0.75(每周期按365天計算).運用內點算法,并借助Matlab2014a軟件進行求解,可得最優零售價格、最優訂購周期及最優缺貨時間的數值解,及零售商單位時間的平均總利潤最大值如下表2.

表2:各種情形下對應的零售商的最優決策

可得,不同情形下,零售商的最優訂購量為

分析可知在貸款全部獲得延期支付的最小訂購量取對應值下,零售商的最優缺貨時間、最優訂購周期、最優零售價格及訂購周期內年最大利潤,如下表3.

表3:貸款全部獲得延期支付最小訂購量Qd對缺貨時間、訂購周期、零售價格及零售商利潤影響

5　數值分析

本節通過數值實驗進一步分析采購費用、庫存費用、缺貨費用及腐蝕率對最優缺貨時間、最優訂購周期、最優零售價格及零售商年最大利潤的影響,如下表4–7.假設所對應的參數值和4.2節中的相同,不失一般性,僅M ≤t1＜T(Q+S≥Qd)情形下進行討論.

表4:采購費用對缺貨時間、訂購周期、零售價格及零售商利潤的影響

表5:庫存成本對缺貨時間、訂購周期、零售價格及零售商利潤的影響

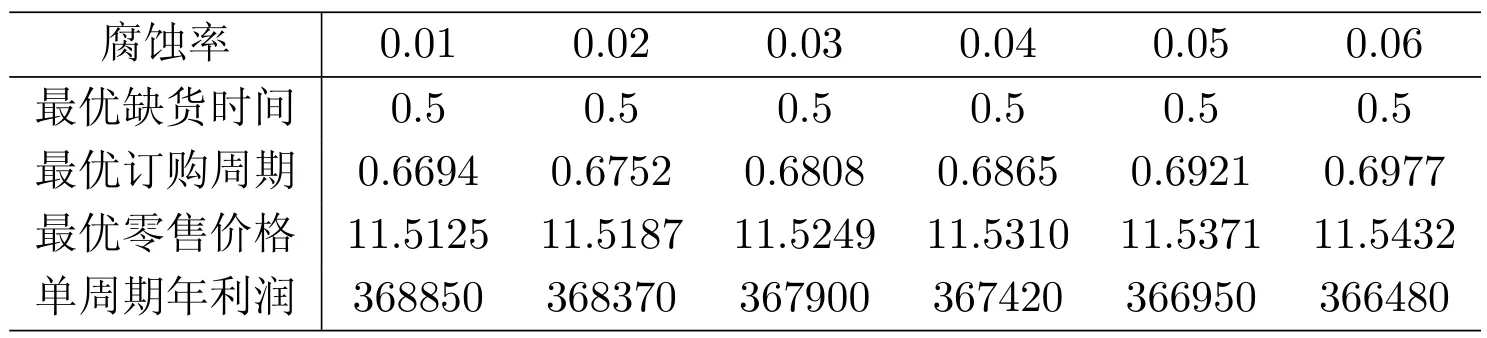
表6:腐蝕率對缺貨時間、訂購周期、零售價格及零售商利潤的影響

由表4、5、6可知,最優缺貨時刻隨著單周期內固定采購費用、庫存成本及腐蝕率的增加而不變;最優訂購周期及最優零售價格隨著單周期內固定采購費用、庫存成本及腐蝕率的增加而增加;零售商年利潤隨著單周期內固定采購費用、庫存成本及腐蝕率的增加而減少.

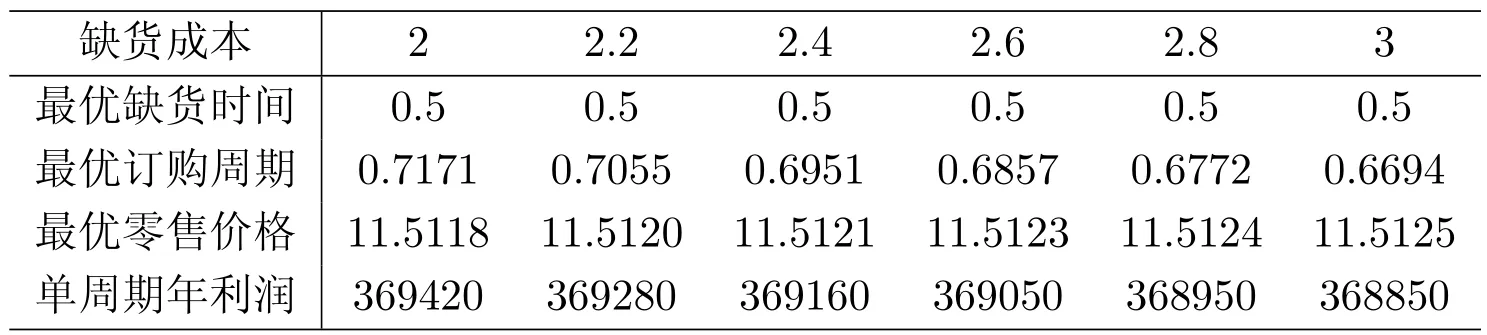
表7:缺貨成本對缺貨時間、訂購周期、零售價格及零售商利潤的影響

由表7可知,最優缺貨時刻隨著缺貨成本的增加而不變;最優零售價格隨著單周期內缺貨成本的增加而增加;最優訂購周期及零售商年利潤隨著缺貨成本的增加而減少.

根據以上的數值分析,可以得到以下管理見解:

第一 單周期固定采購費用、庫存成本及腐蝕率越少,缺貨成本越多,則缺貨時間越短.

第二 單周期固定采購費用、庫存成本及腐蝕率越少,缺貨成本越多,則訂購周期越短.

第三 單周期固定采購費用、庫存成本、腐蝕率及缺貨成本越多,則零售價格越大.

第四 單周期固定采購費用、庫存成本、腐蝕率及缺貨成本越多,則零售商年利潤越小.

6　結論

當零售商面臨資金約束,零售商很難從銀行等外部渠道獲得融資時,如何實現內部融資是供應鏈金融研究的熱點.因此,供應商對零售商提供延期支付優惠策略來刺激其訂購行為,且延期支付的期限與訂購量相關.首先,針對易腐產品,且允許缺貨發生、零售價格影響市場需求量情形下,建立了相應的庫存決策模型.其次,在易腐率很小的情況下,對目標函數進行二階泰勒展開,并運用微積分及矩陣論知識,在訂購周期固定的條件下,獲得了的零售商最優缺貨時間、最優零售價格及年平均最大利潤的解析解.然后,在易腐率比較大的情況下,借助內點算法,獲得了零售商最優決策的數值解.最后,通過數值實驗分析單周期內固定采購費用、庫存成本、腐蝕率及缺貨成本對零售商最優決策的影響,可得單周期內固定采購費用、庫存成本、腐蝕率及缺貨成本越少,對零售商和客戶越有利.

該模型在實際生活中有如下幾方面的應用價值:①供應商可以根據日常中的具體情況,通過改變貸款全部獲得延期支付的最小訂購量來調控零售商的訂購量.②當產品發生缺貨時,零售商可以確定適當的缺貨時間、訂購周期及零售價格來實現其年利潤的最大化,為零售商在庫存管理方面提供了理論支持.③對易腐產品庫存管理方面的問題,借助文中的算法可以很容易獲取零售商的最優決策.同時,本模型可以進一步擴展,如解決多階段多產品庫存問題.

[1]王文利.需求不確定下的供應鏈融資研究―基于報童模型視角[M].北京:中國金融出版社,2014.

[2]李明芳,王道平.延期支付期限與訂貨量相關情形下的EOQ模型[J].系統管理學報,2011,20(4):389–397.

[3]Goyal S K.Economic order quantity under conditions of permissible delay in payments[J].J.Oper.Res.Soc.,1985,36(4):335–338.

[4]Chung K J.A theorem on the determination of economic order quantity under conditions of permissible delay in payments[J].Comp.Oper.Res.,1998,25(1):49–52.

[5]Huang Y.Optimal retailer’s replenishment decisions in the EPQ model under two levels of trade credit policy[J].Euro.J.Oper.Res.,2007,176(3):1577–1591.

[6]Chen S,C′ardenas-Barr′on L E.Teng J.Retailer’s economic order quantity when the supplier offers conditionally permissible delay in payments link to order quantity[J].Intern.J.Prod.Econ.,2014,155:284–291.

[7]李明芳,王道平,李鋒.基于現金折扣和延期支付條件下變質產品的補貨策略[J].管理評論,2011,23(4):122–128.

[8]Sana S S,Chaudhuri K S.A deterministic EOQ model with delays in payments and price-discount offers[J].Euro.J.Oper.Res.,2008,184(2):509–533.

[9]Dye C,Ouyang L.A particle swarm optimization for solving joint pricing and lot-sizing problem with fluctuating demand and trade credit financing[J].Comput.Indus.Engin.,2011,60(1):127–137.

[10]李明芳,王道平.延期支付條件下零售商的最優售價和訂貨策略[J].運籌與管理,2011,20(06):59–65.

[11]梁培培,孫延明.需求基于瞬時庫存的延期支付策略設計[J].統計與決策,2015,30(06):41–43.

[12]Shukla H S,Shukla V and Yadav S K.Optimal ordering policies in the EOQ(economic order quantity)model with time-dependent demand rate under permissible delay in payments[J].Intern.J.Modern Engin.Sci.,2015,4(1):1–3.

[13]Shukla H S,Tripathi R P,Siddiqui A.EOQ model with inventory level dependent demand rate under permissible delay in payments with cash discount[J].Indian J.Sci.Tech.,2015,8(28).

[14]周永務,王圣東.庫存控制理論與方法[M].北京:科學出版社,2009.

[15]馬昌鳳.最優化方法及其Matlab程序設計[M].北京:科學出版社,2009.

[16]雍龍泉,鄧方安,陳濤.單調線性互補問題的一種內點算法[J].數學雜志,2009,29(5):681–686.

[17]龔小玉,張明望.非單調線性互補問題的高階寬領域內點算法[J].數學雜志,2009,29(2):217–223.