有關Ramanujan Tau函數的注記

程開敏

(西華師范大學數學與信息學院,四川南充 637002)

1　引言

設q=eπiτ,其中τ∈C 且Im(τ)＞0.對任意的q,z∈C,如下定義(z;q)∞:

將形如

的q-級數稱為Lambert級數.我們知道Ramanujan Tau函數τ:N?→Z是按如下恒等式定義的

Ramanujan理論有很多熱門的研究分支,如Ramanujan-Nagell方程[7].而對τ(n)的研究一直是數論領域的經典研究方向,其中有關τ(n)的顯式表達式及其同余性質的研究就是很多數論學者的研究興趣之一.Berndt[2]等人得到了τ(n)模211,36,53,7,23的若干同余式.設n,k為正整數,記因子和函數

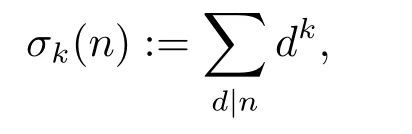
tk(n)表示將n表為k個三角數的和的表法數,rk(n)表示將n表為k個平方數的和的表法數,則值得一提的是,Apostol[1]給出了表達式

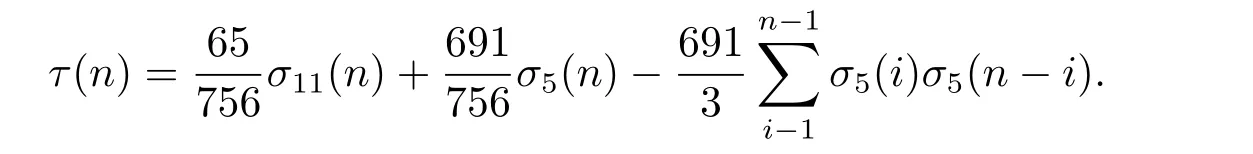
Ewell[5,6]也分別得到了以下兩個恒等式

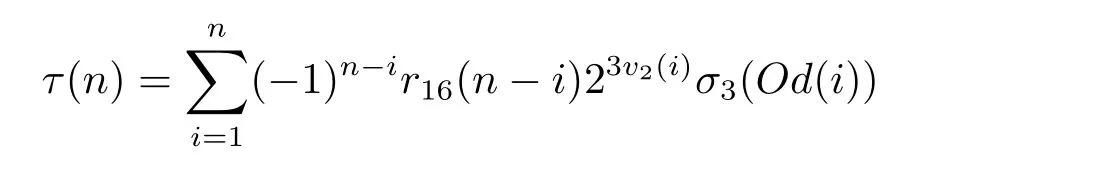
和

其中v2(n)為n的2-adic賦值,Od(n)為n的奇數部分,即Od(n)=n×2?v2(n).最近,作者[8]利用Ewell的一個恒等式,也得到一個Ramanujan Tau函數的新表達式.

在本文中,我們主要對若干特殊的theta函數和q-級數進行研究.我們建立了幾類特殊的q-級數與Ramanujan Tau函數的生成函數的關系.從而得到了幾個Ramanujan Tau函數新的顯式表達式,其中這些表達式中只含因子和函數,另外,作為定理的應用,還得到Ramanujan Tau函數的同余恒等式.

2　基本知識及引理

設q=eπiτ,其中τ∈C 且Im(τ)＞0.先定義以下三個theta函數

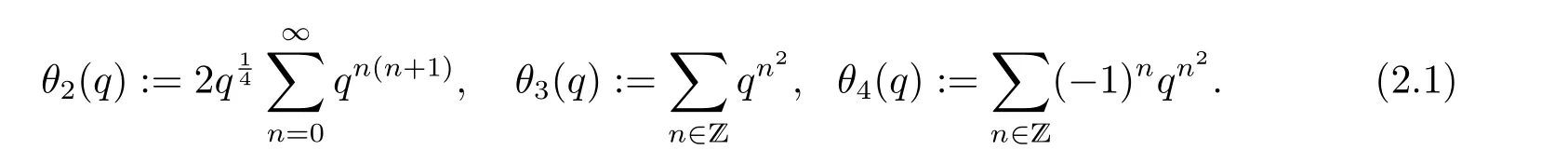
容易檢驗以下恒等式成立

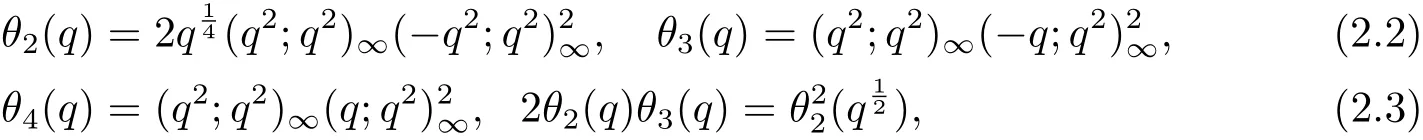
其中符號(·;·)∞如(1.1)式定義.又如下定義φ(q)和ψ(q)

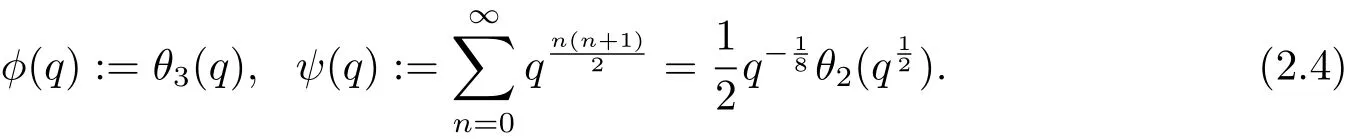
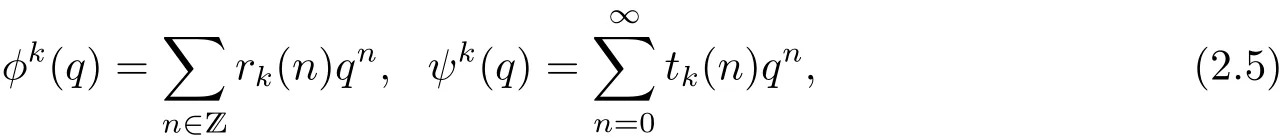
設k為正整數,則有其中tk(n)表示將n表為k個三角數的和的表法數,rk(n)表示將n表為k個平方數的和的表法數.最后定義兩類特殊的Lambert級數如下

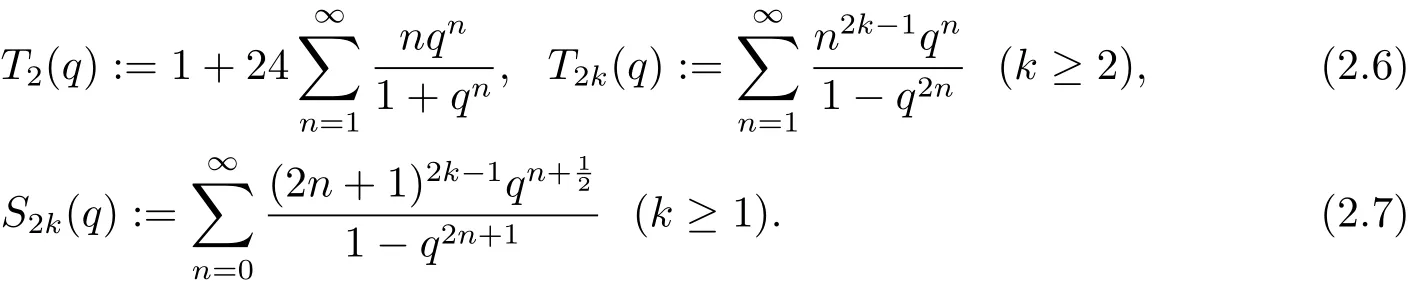
現在給出幾個有用的結論.

引理2.1[3]設φ(q)和ψ(q)是由(2.4)式定義的q-級數,則以下恒等式成立.

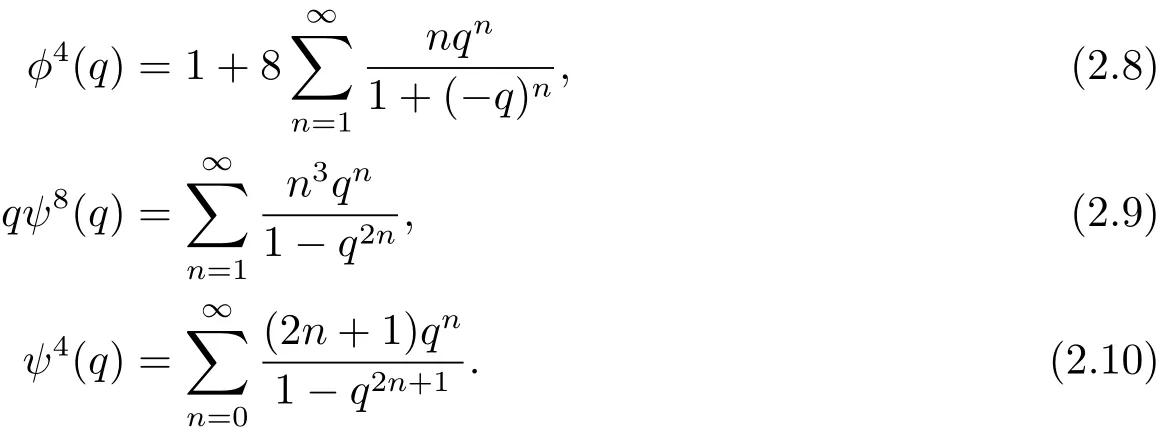
命題2.2設θ2(q)和θ3(q)是由(2.1)式定義的theta函數,則以下恒等式成立

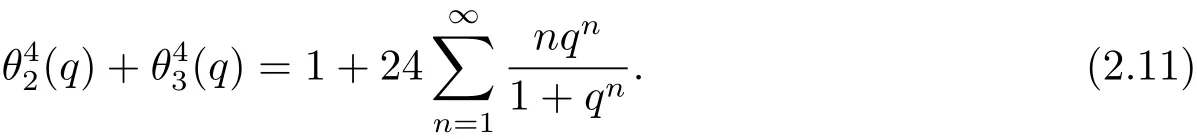
證由ψ(q),φ(q)的定義式(2.4)及引理2.1,可知

所以(2.11)式成立.

引理2.3[4]設T2k(q)和S2k(q)是由(2.6)和(2.7)式定義的q-級數,則以下遞推恒等式成立

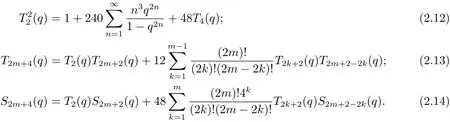
現在利用引理2.3建立Lambet級數S2k(q),T2k(q)與theta函數θ2(q),θ3(q)之間的等式關系.為了敘述方便,記

則由T2k(q)的定義以及命題2.2的(2.11)式和引理2.1的(2.9)式,易得

再利用引理2.3通過直接計算得

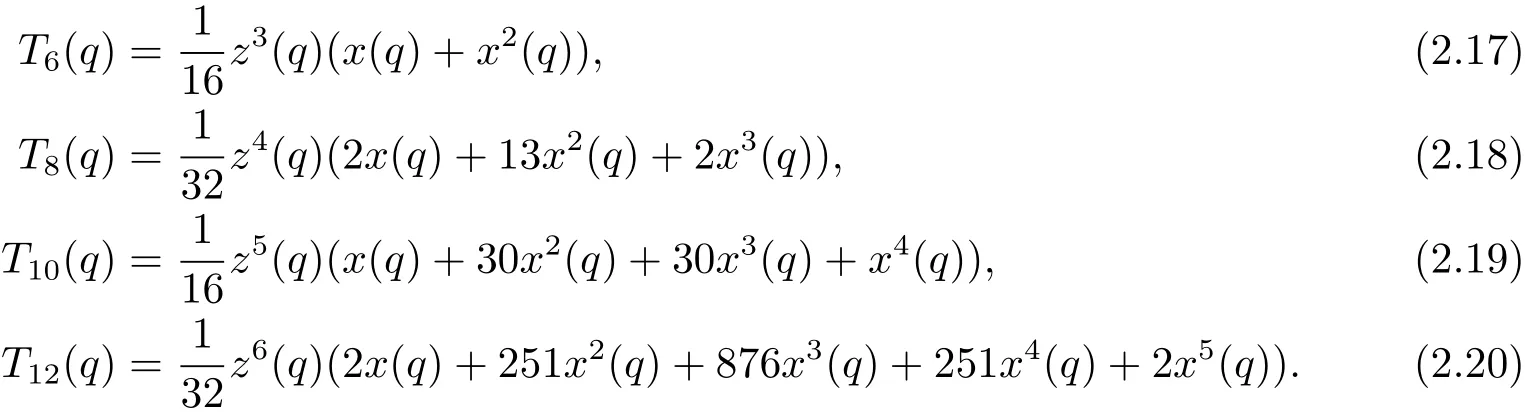
另外,由引理2.1中的(2.10)和(2.3)式中的關系式有

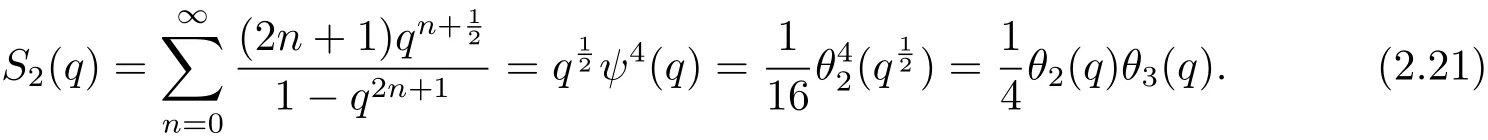
從而

將(2.15)–(2.21)式以及(2.22)式代入到引理2.3的(2.14)式中,可得

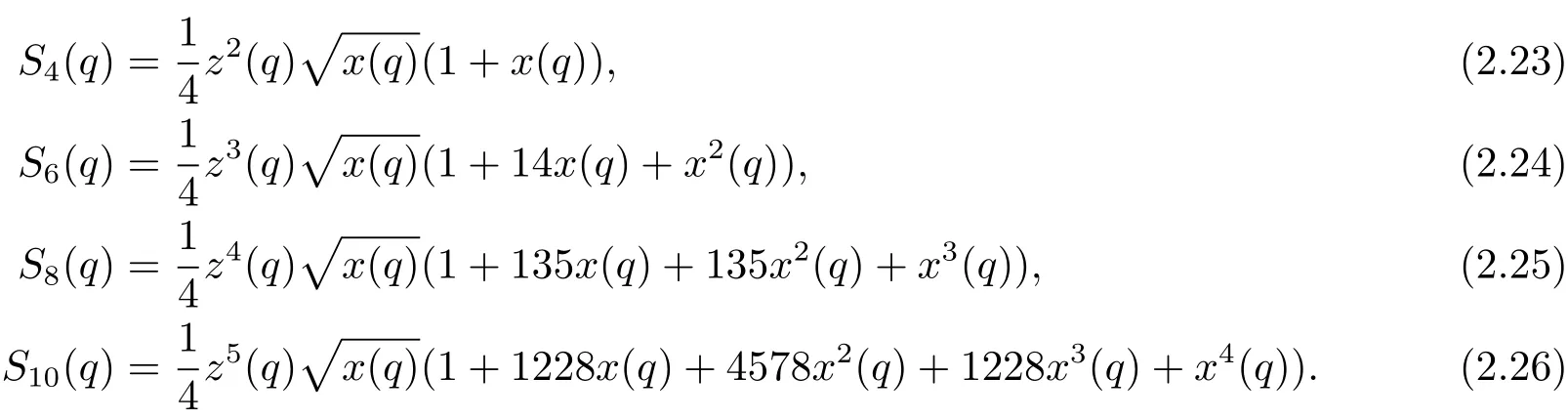
最后,由(2.16)–(2.18)式以及(2.21)式,經過計算發現

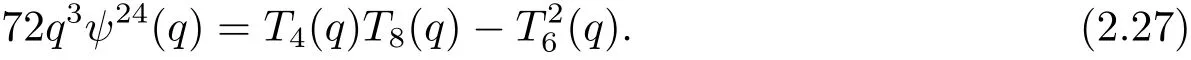
3　主要結果及證明

命題3.1設k為正整數,則以下恒等式成立.

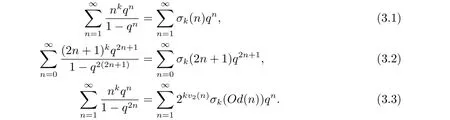
證首先

其次

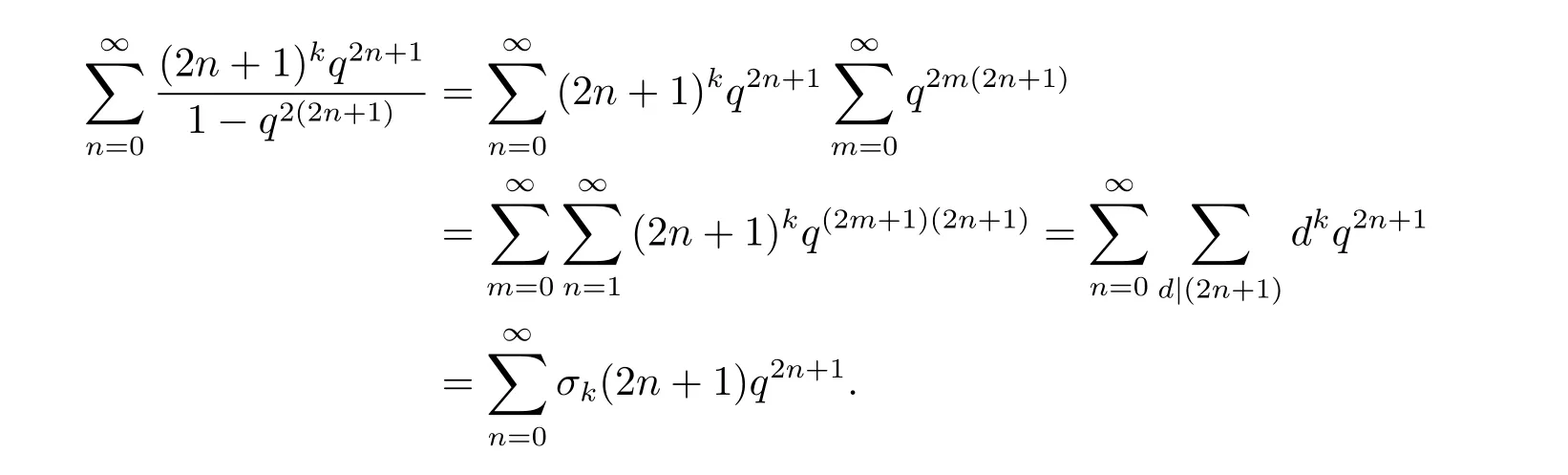
最后

所以命題3.1成立.

定理3.2設n,k為正整數,τ(n)為Ramanujan Tau函數,則有

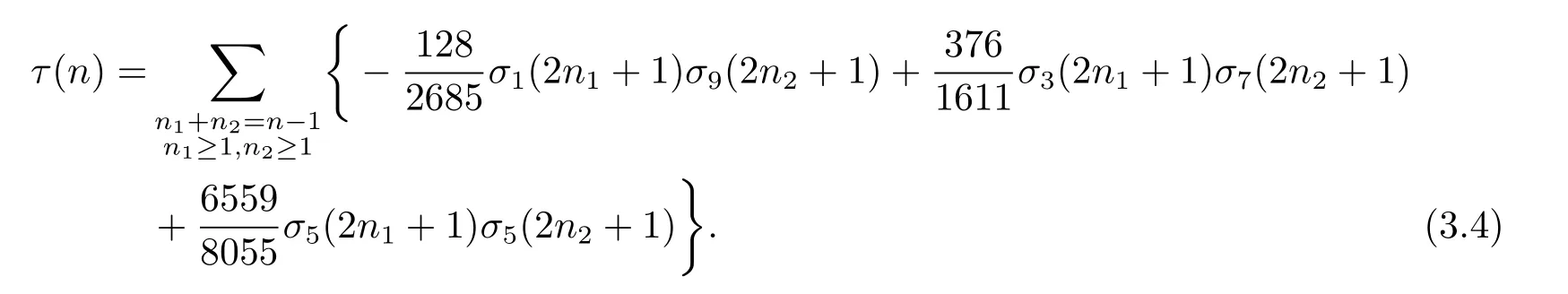
證令一方面,由著名的Jacobi四次恒等式

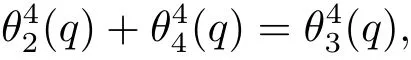
并結合(2.2)和(2.3)式,得

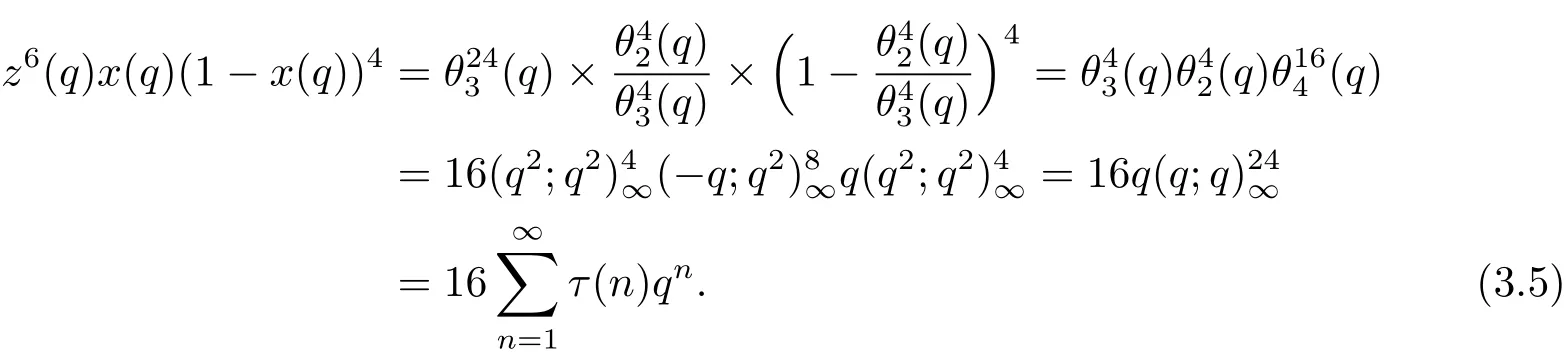
另一方面,觀察到S2(q)S10(q),S4(q)S8(q),(q)與z6(q)x(q)(1?x(q))4均含有因子z6(q).所以不妨設

其中A1,A2,A3∈Q為待定系數.將(2.23)–(2.26)式分別代入到(3.6)式的左邊,然后比較(3.6)式的左右兩邊的項z6(q)xi(q)(i=1,2,3,4,5)的系數,解得

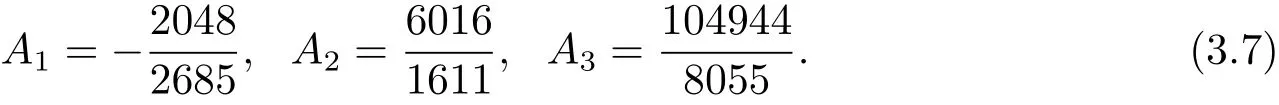
并且由引理3.1,可知

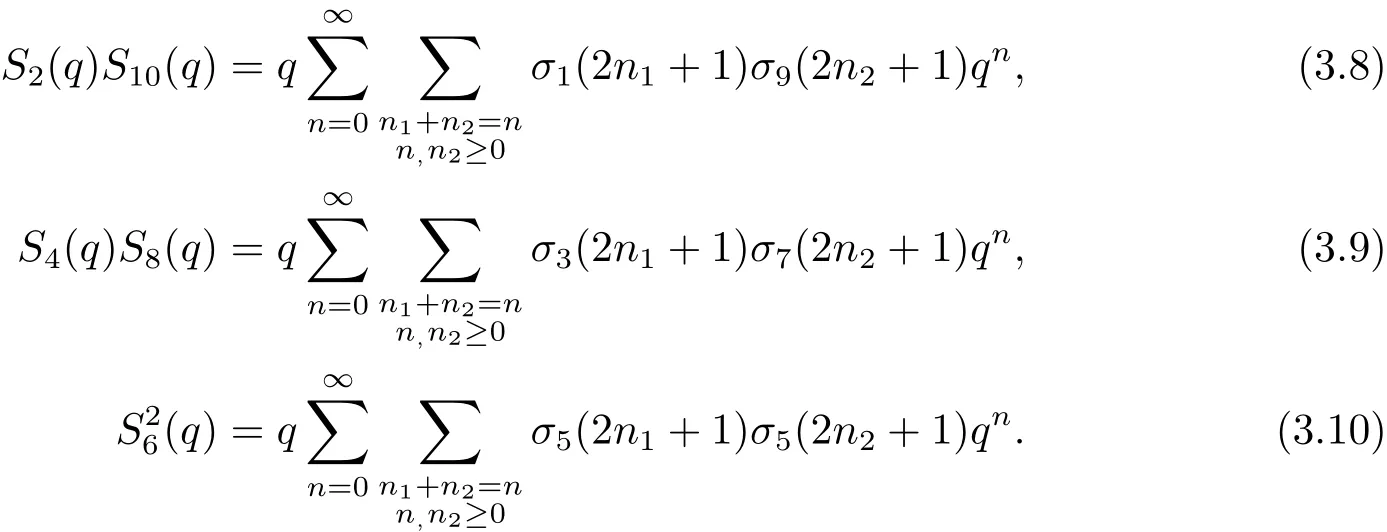
所以綜合(3.5)–(3.10)式,有

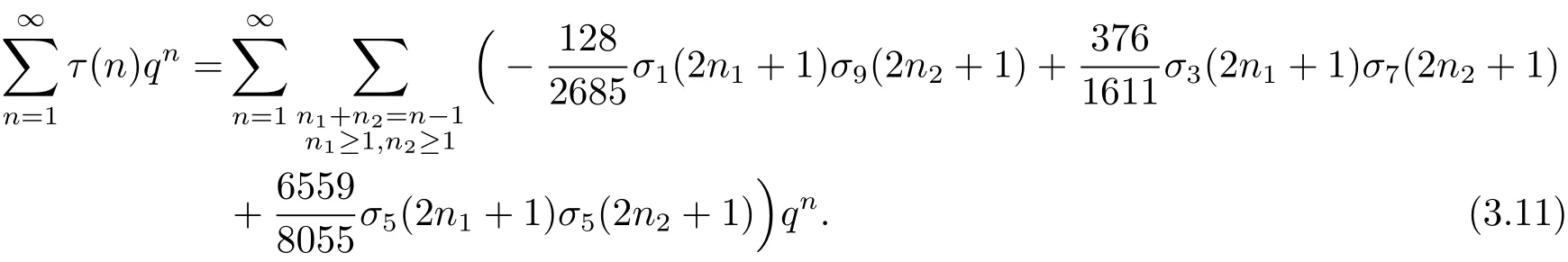
最后比較(3.11)左右兩邊qn的系數立即可得定理3.2的結論.

定理3.3設n,k為正整數,τ(n)為Ramanujan Tau函數為將n表為k個三角數的和的表法數,v2(n)為n的2-adic賦值,則對任意的n≥3,有

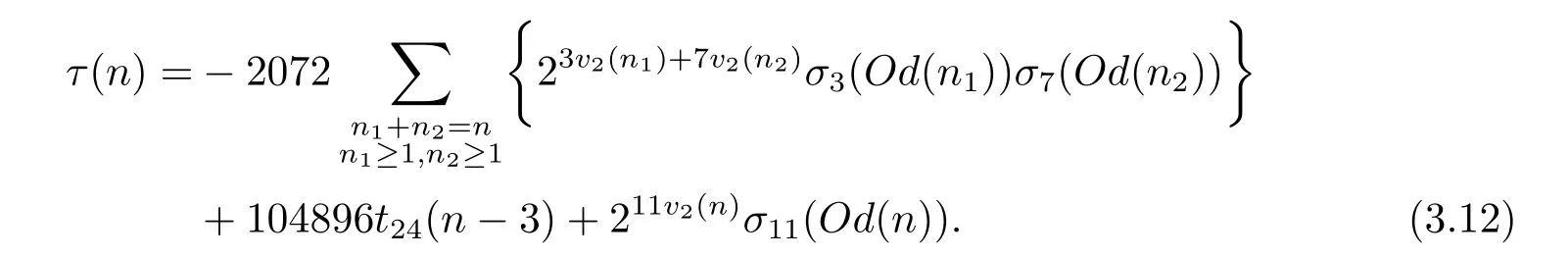
證通過利用(2.16),(2.18),(2.20)以及(2.27)式,觀察到S4(q)S8(q),q3ψ24(q),T12(q)與z6(q)x(q)(1?x(q))4均含有因子z6(q).所以不妨設

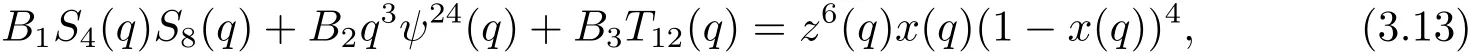
其中B1,B2,B3∈Q為待定系數.將(2.16),(2.18),(2.20)以及(2.27)式分別代入到(3.13)式的左邊,然后比較(3.13)式的左右兩邊的項z6(q)xi(q)(i=1,2,3,4,5)的系數,解得

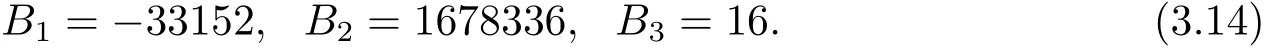
并且由引理3.1,可知

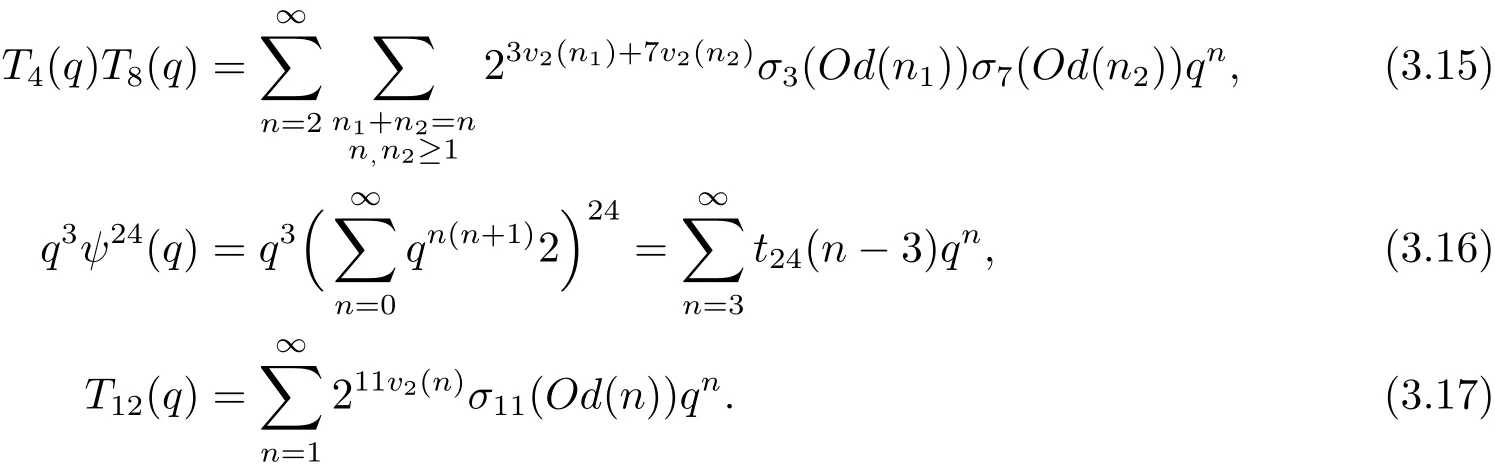
所以綜合(3.5),(3.13)–(3.17)式,有

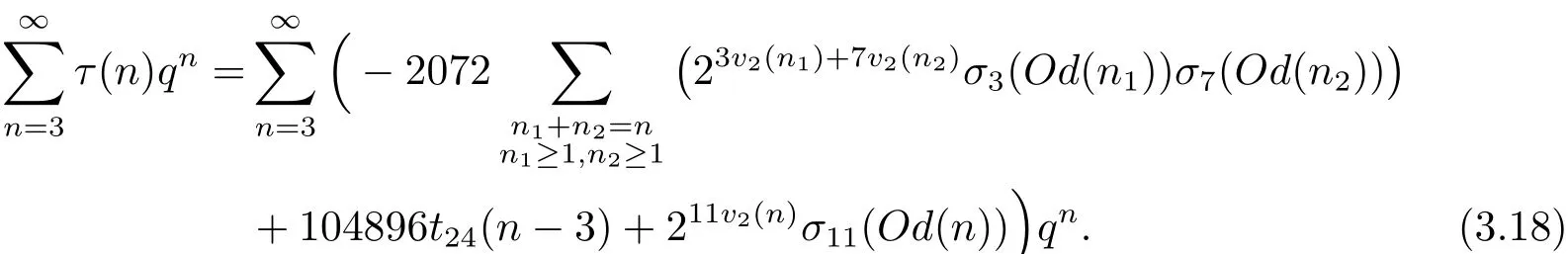
最后比較(3.18)式左右兩邊qn的系數立即可得定理3.3的結論.

由定理3.3立即得到以下同余恒等式.

推論3.4設n,k為正整數,τ(n)為Ramanujan Tau函數,則對任意的n≥3都有

[1]Apostol T M.Modular functions and dirichlet series in number theory(2nd ed.)[M].New York:Springer-Verlag,1997.

[2]Berndt B C,Ken Ono.Ramanujan’s unpublished manuscript on the partition and tau functions with proofs and commentary[J].S′em.Lothar.Combin.，1999,42:1–63.

[3]Berndt B C.Ramanujan’s notebook(part III)[M].New York:Springer-Verlag,1991.

[4]Chan H,Chua K.Representations of integers as sums of 32 squares[J].Ramanujan J.,2003,7:79–89.

[5]Ewell J.New representations of Ramanujan’s tau function[J].Proc.Amer.Math.Soc.,1999,128:723–726.

[6]Ewell J.A formulae for Ramanujan’s tau function[J].Proc.Amer.Math.Soc.,1984,91:37–40.

[7]陳候炎.關于廣義Ramanujan-Nagell方程的一個猜想[J].數學雜志,2010,30(3):567–570.

[8]程開敏.一個Ramanujan Tau函數的新表達式[J].純粹數學與應用數學,2017,33(2):129–133.