具有隨機(jī)擾動(dòng)的Lotka-Volterra競(jìng)爭(zhēng)模型的參數(shù)估計(jì)

馬永剛,張啟敏,劉俊梅

(1.寧夏大學(xué)數(shù)學(xué)統(tǒng)計(jì)學(xué)院,寧夏銀川 750021)

(2.榆林學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,陜西榆林 719000)

1　引言

隨機(jī)微分方程是近幾年熱門(mén)的數(shù)學(xué)學(xué)科,它是微分方程、動(dòng)力系統(tǒng)及隨機(jī)分析相互交叉的學(xué)科.在實(shí)際應(yīng)用中,隨機(jī)微分方程的參數(shù)一般是未知的,因此參數(shù)估計(jì)問(wèn)題成為一個(gè)重要的研究方向.關(guān)于此類方程參數(shù)估計(jì)問(wèn)題已有很多結(jié)果,見(jiàn)文獻(xiàn)[1–3,9]等.在文獻(xiàn)[1]中,Bishwal詳細(xì)介紹了參數(shù)估計(jì)的理論方法和技巧,并運(yùn)用到各種隨機(jī)模型中.在文獻(xiàn)[3]中,作者基于采樣的時(shí)間序列討論了非線性隨機(jī)微分方程的參數(shù)估計(jì)問(wèn)題.

1926年意大利數(shù)學(xué)家Volterra提出著名的Lotka-Volterra微分方程模型,該模型引起眾多生物學(xué)家、數(shù)學(xué)家極大的興趣.Lotka-Volterra模型所表現(xiàn)的生態(tài)學(xué)現(xiàn)象,在自然界中處處可見(jiàn).例如,病蟲(chóng)害的周期爆發(fā),農(nóng)作物的豐收年與低產(chǎn)年的周期循環(huán),動(dòng)物之間的捕食與被捕食等,這些現(xiàn)象都是Lotka-Volterra模型變化規(guī)律的具體展示.Lotka-Volterra模型的一般形式為[4]

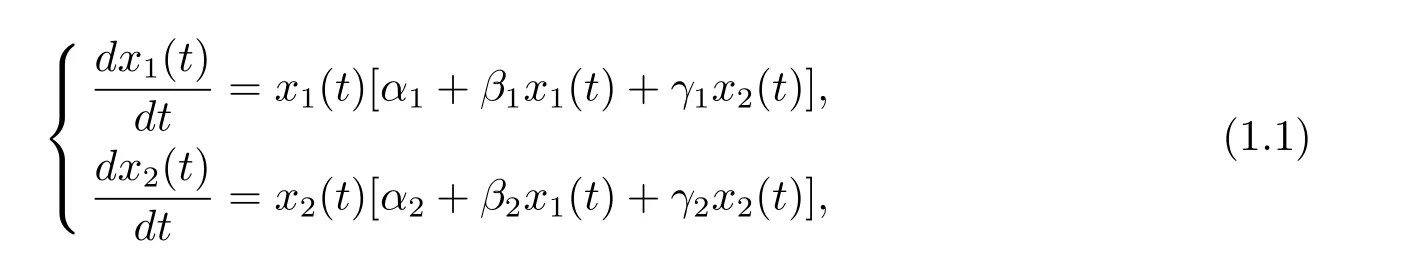
其中αi,βi,γi(i=1,2)均為常數(shù),α1與α2分別表示兩種群的內(nèi)稟增長(zhǎng)率,β1與γ2分別表示種內(nèi)作用系數(shù),γ1與β2分別表示種間作用系數(shù).就其生態(tài)意義可分為三類:競(jìng)爭(zhēng)模型(αi＞ 0,βi＜ 0,γi＜ 0,i=1,2)、互惠模型 (αi＞ 0,βi＜ 0,γi＞ 0,i=1,2)、捕食 -被捕食模型(αi＞ 0,βi＜ 0,γ1＜ 0,γ2＞ 0,i=1,2).基于此模型,各種形式的Lotka-Volterra生態(tài)模型被提出,其中一類是受外界隨機(jī)因素影響的Lotka-Volterra生態(tài)模型.下面研究白噪聲擾動(dòng)的Lotka-Volterra競(jìng)爭(zhēng)模型[5]

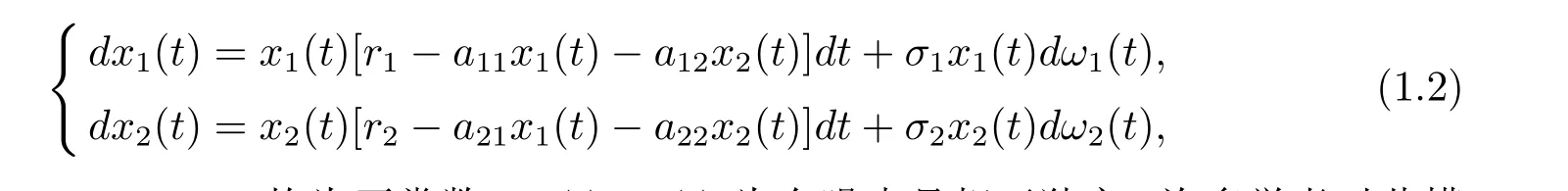
其中r1,r2,a11,a12,a21,a22均為正常數(shù),ω1(t),ω2(t)為白噪聲且相互獨(dú)立.許多學(xué)者對(duì)此模型進(jìn)行了研究,見(jiàn)文獻(xiàn)[4,5,6]等.其中最重要的結(jié)果之一,種群隨機(jī)持久生存,需要滿足下面條件

其中

當(dāng)上述條件變?yōu)?/p>

兩種群中至少有一個(gè)種群隨機(jī)滅絕.

本文主要研究隨機(jī)種群Lotka-Volterra競(jìng)爭(zhēng)模型的參數(shù)估計(jì),即對(duì)方程組(1.2)中參數(shù)r1,a11,a12,r2,a21,a22,σ1,σ2應(yīng)用最小二乘法理論進(jìn)行估計(jì),得到較好的估計(jì)結(jié)果.主要結(jié)果是參數(shù)的點(diǎn)估計(jì)值和區(qū)間估計(jì),同時(shí)獲得影響估計(jì)區(qū)間長(zhǎng)度的主要因素.最后給出了數(shù)值模擬,結(jié)果表明了該方法的可行性與有效性.

2　回歸模型

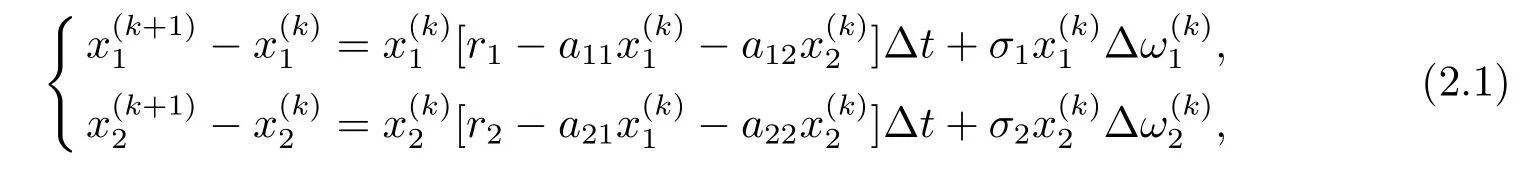
其中方程組(2.1)可轉(zhuǎn)化為

其中

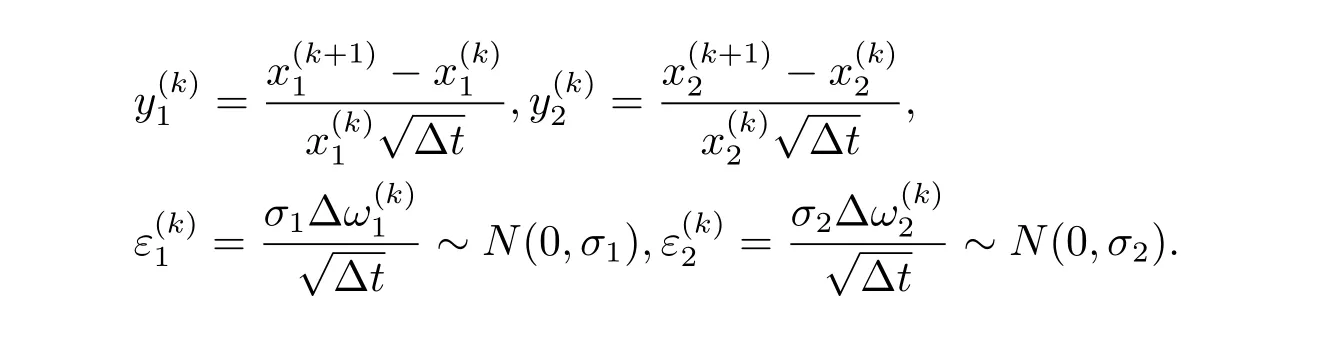
進(jìn)一步方程組(2.2)表示為

方程組(2.3)是簡(jiǎn)單的線性回歸模型,應(yīng)用線性回歸理論的方法估計(jì)參數(shù),估計(jì)過(guò)程基于最小二乘法,使下面兩個(gè)式子的值越小越好

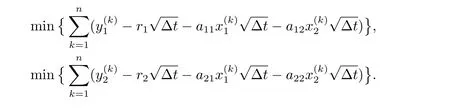
為計(jì)算方便,方程(2.3)可寫(xiě)成分塊矩陣的形式

其中

在塊矩陣中,子矩陣分別為

3　點(diǎn)估計(jì)

由多元線性回歸理論的公式估計(jì)參數(shù)β和η:

記

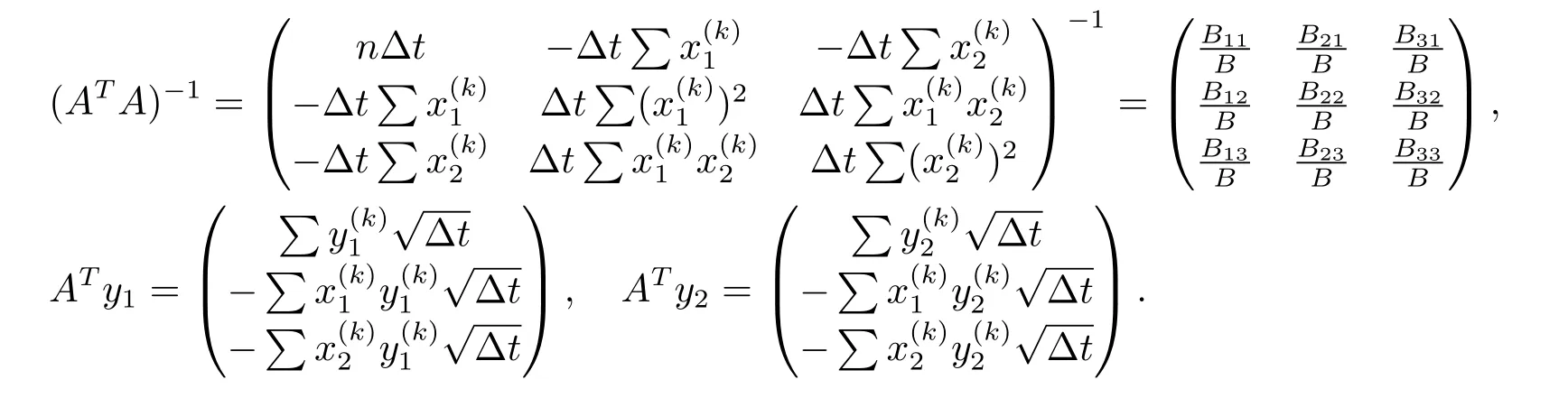
故(3.1)式可進(jìn)一步化簡(jiǎn)為

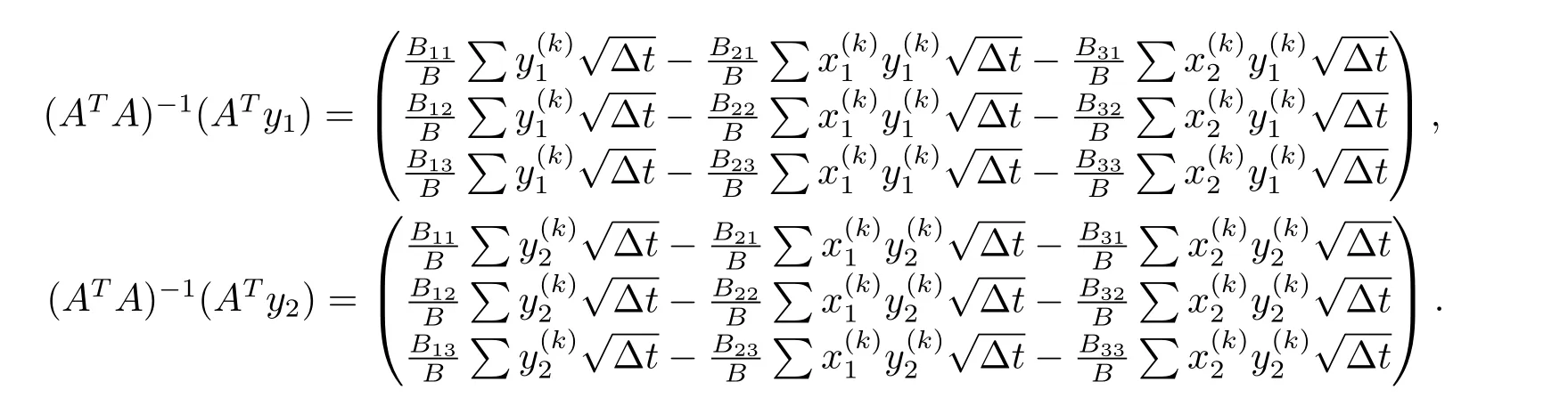
為了獲得參數(shù)的置信區(qū)間,需要估計(jì)參數(shù)β和η的方差,方差估計(jì)公式為

估計(jì)得到,p為被估計(jì)參數(shù)個(gè)數(shù).由(3.1),(3.3)式可得

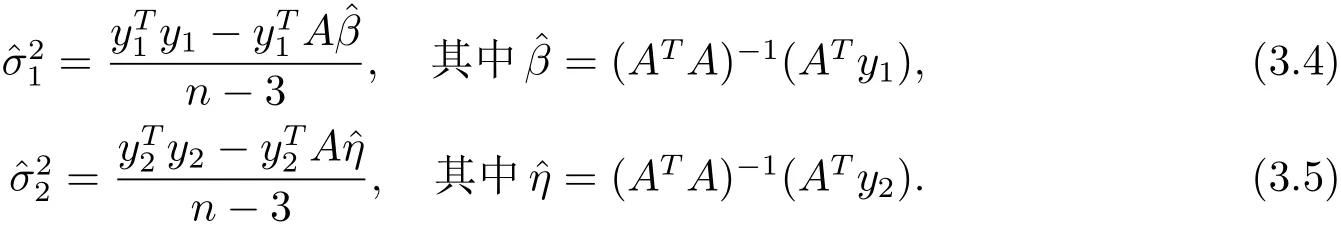
等式(3.4),(3.5)化簡(jiǎn)得

定理3.1方程組(3.6)中分別為方程組(2.1)中參數(shù)的漸進(jìn)無(wú)偏估計(jì),即當(dāng)n→∞,

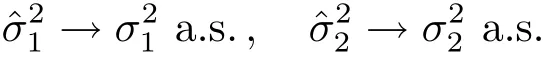
證類似文獻(xiàn)[7]證明.利用分別估計(jì)(3.2)式中參數(shù)得到被估參數(shù)的方差

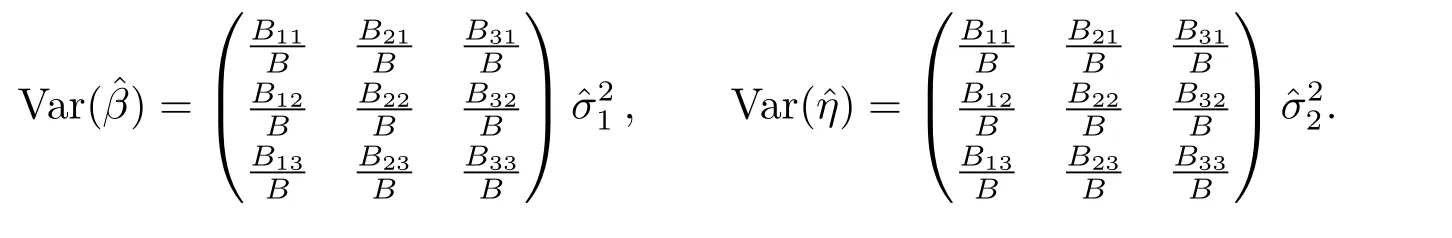
4　區(qū)間估計(jì)

如果σ2已知,由最小二乘法回歸理論[8],參數(shù)估計(jì)值?β,?η的各分量都滿足正態(tài)分布.當(dāng)觀察值的數(shù)量n足夠大時(shí),可由?σ2代替σ2,因此(1?α)的置信區(qū)間(CIs)分別為

下面給出具體數(shù)據(jù),進(jìn)行參數(shù)的估計(jì).

例1在模型(1.2)式中,我們選擇滿足種群持久生存的數(shù)據(jù)進(jìn)行模擬,即兩種群隨機(jī)持久存在的情形,其它狀態(tài)的數(shù)據(jù)也可獲得類似結(jié)論.假設(shè)參數(shù)真實(shí)值分別為r1=1,a11=0.3,a12=0.2,σ1=0.04,r2=1.2,a21=0.3,a22=0.4,σ2=0.05, 初始值為x1(0)=1.5,x2(0)=2.應(yīng)用這些參數(shù)的值,通過(guò)Euler-Maruyama方法離散,我們獲得三組模擬數(shù)值xk1(t),xk2(t),數(shù)量分別為(A)n=5000;(B)n=10000;(C)n=50000;保存這些數(shù)據(jù)為模擬數(shù)據(jù)集.對(duì)每一組數(shù)據(jù),給步長(zhǎng)?t=0.02,0.05,0.1進(jìn)行模擬,給出一些模擬結(jié)果,以便比較真實(shí)值與估計(jì)值.在表1–4中,樣本的大小以符號(hào)“Size n”表示,且在表中第一列給出.其中表1,2樣本大小從5000增加到50000,在每一組模擬數(shù)據(jù)中,分別以三種不同步長(zhǎng)進(jìn)行模擬.模擬數(shù)據(jù)表明參數(shù)的估計(jì)值與真實(shí)值沒(méi)有明顯區(qū)別,絕對(duì)誤差與樣本大小有關(guān),與步長(zhǎng)?t無(wú)關(guān),且隨著樣本數(shù)量的增大,絕對(duì)誤差越來(lái)越小.

表1:(r1,a11,a12)的估計(jì)模擬結(jié)果(真實(shí)值:r1=1,a11=0.3,a12=0.2)

表2:(r2,a21,a22)的估計(jì)模擬結(jié)果(真實(shí)值:r2=1,a21=0.3,a22=0.2)

其次給出各個(gè)參數(shù)置信水平為0.95的置信區(qū)間的一些模擬結(jié)果.表3,4中,給出參數(shù)的估計(jì)區(qū)間及區(qū)間長(zhǎng)度,模擬數(shù)據(jù)表明隨著樣本量的增大,置信水平長(zhǎng)度越來(lái)越小.

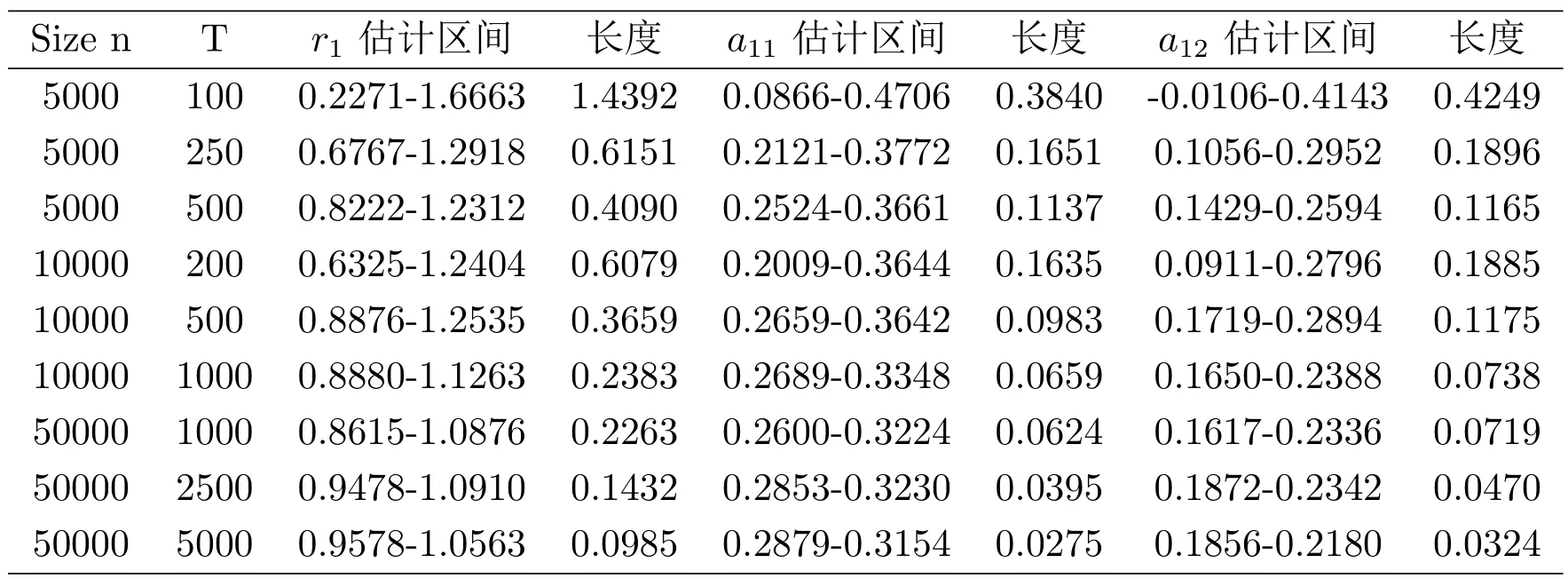
表3:置信水平為0.95的參數(shù)r1,a11,a12置信區(qū)間模擬結(jié)果(真實(shí)值:r1=1,a11=0.3,a12=0.2)

表4:置信水平為0.95的參數(shù)r2,a21,a22置信區(qū)間模擬結(jié)果(真實(shí)值:r2=1,a21=0.3,a22=0.2)

5　結(jié)論

本文對(duì)隨機(jī)兩種群Lotka-Volterra競(jìng)爭(zhēng)模型應(yīng)用最小二乘法理論進(jìn)行參數(shù)估計(jì),獲得參數(shù)r1,a11,a12,r2,a21,a22,σ1,σ2的估計(jì)值及估計(jì)區(qū)間.通過(guò)觀察結(jié)果,得到影響置信區(qū)間長(zhǎng)度的主要因素.結(jié)果表明,參數(shù)估計(jì)區(qū)間的長(zhǎng)度隨著樣本數(shù)量n的增加而減小,不依賴步長(zhǎng)?t的長(zhǎng)度.例1給出了具體的數(shù)值模擬.極大似然估計(jì)與貝葉斯估計(jì)方法是另外兩種參數(shù)估計(jì)的方法,在將來(lái)的工作中,將應(yīng)用這些方法到隨機(jī)兩種群Lotka-Volterra模型.

[1]Bishwal JPN.Parameter estimation in stochastic differential equations[M].Berlin:Springer,2008.

[2]Kristensen NR,Madsen H,Young PC.Parameter estimation in stochastic grey-box model[J].Automatica,2004,40(2):225–237.

[3]Timmer J.Parameter estimation in nonlinear stochastic differential equatuons[J].Chaos Sol.Fract.,2000,11(15):2571–2578.

[4]Zhu C,Yin G.On competitive Lotka-Volterra model in random environments[J].J.Math.Anal.Appl.,2009,357(1):154–170.

[5]Jiang D Q,Ji C Y,Li X,O’Regan D.Analysis of autonomous Lotka-Volterra competition systems with random perturbation[J].J.Math.Anal.Appl.,2012,390:582–595.

[6]王佳,丁潔麗.Logistic回歸模型中參數(shù)極大似然估計(jì)的二次下界算法及其應(yīng)用[J].數(shù)學(xué)雜志,2015,35(6):1521–1532

[7]Pan J F,Alison G,David G,Mao X R.Parameter estimation for the stochastic SIS epidemic model[J].Stat.Infer.Stoch Proc.,2014,17(1):75–98.

[8]Rawlings JO.Applied regression analysis:a research tool[M].Belmont,CA:Wadsworth,1988.

[9]洪志敏,閆在在.Volterra積分方程的蒙特卡羅數(shù)值求解方法[J].數(shù)學(xué)雜志,2016,36(2):425–436.