世界黃金價格波動特征研究

柴芳柔

摘要：文章使用半參數隨機波動率模型（SPM），對2003年1月1日至2017年8月10日期間世界黃金價格波動特征進行了實證分析。模型擬合檢驗結論表明，SPM模型能夠很好地擬合世界黃金價格波動過程當中存在的尖峰厚尾性、波動聚集性和非對稱性等金融數據特征。采用基于貝葉斯的MCMC方法對模型進行參數估計，通過進一步與SV-N和SV-T模型對比分析，結果顯示SPM對于世界黃金價格波動特征刻畫要明顯優于SV-N和SV-T模型。

關鍵詞：黃金期貨；半參數隨機波動率模型；MCMC

一、引言

黃金是同時具有商品、貨幣以及投資屬性的一種特殊商品，可用于資產儲備和投資增值。自2002年上海黃金交易所成立以來，我國黃金市場逐步市場化，與世界接軌，為投資者與投資機構提供了良好的平臺。目前黃金期貨市場交易量和交易額持續增多，起到了很好的風險發散作用。黃金不僅具有商品屬性，還具有金融屬性，其波動性不僅影響人民生活穩定還影響金融穩定，其市場健康發展對于國家金融系統穩定非常重要，所以對黃金期貨市場的科學研究是刻不容緩的。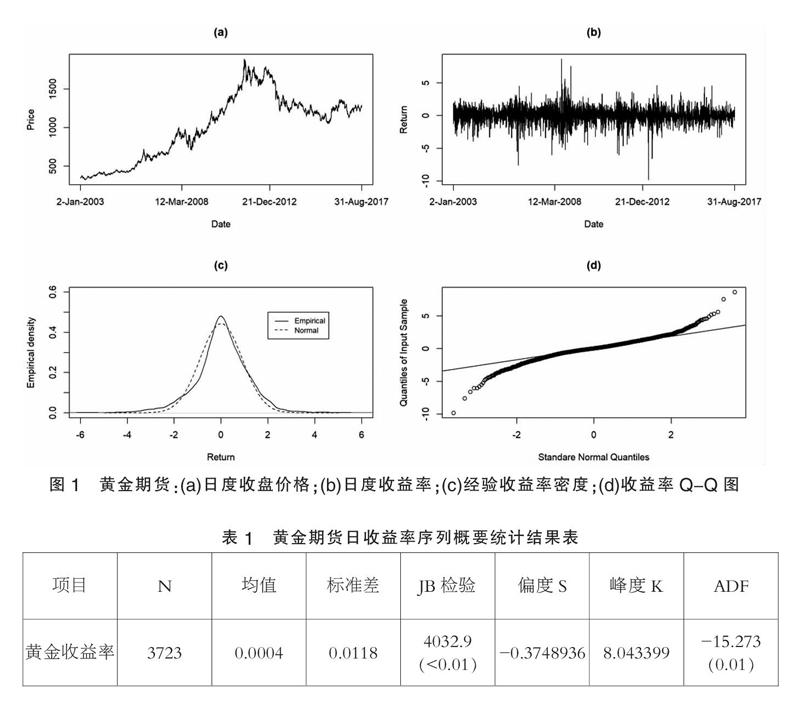

目前，對黃金期貨收益率波動特征的研究并不多見。陳楊林等（2008）應用GARCH與SV-T模型對世界黃金價格的走勢與波動性進行分析，實證結果表明SV-T模型對世界黃金價格走勢的擬合與預測均優于GARCH模型；Jonathan 等人（2010）選取美國黃金期貨1999～ 2005年高頻樣本作為分析數據，采用 GARCH 模型和 Garman Klass 統計值相結合的方式，探討了該市場日內波動結構；王兆才（2012）研究表明兩狀態MRS-GARCH（1，1）模型的擬合和預測效果均優于單狀態的GARCH模型；孫趙暉（2015）利用SV類模型，以2009年以來的上海黃金交易市場的收益率數據為代表，分析結果認為我國黃金市場波動持續性強且具有尖峰厚尾性，其中Leverage-SV模型擬合效果相對較優；蘇理云等（2017）針對黃金市場呈現的波動持續性等特征，建立SV-POT的組合模型，較為精確地預測了該金融市場的動態Var。

在SV模型中，貝葉斯非參數化方法是一個全新的研究領域，Eleni-Ioanna Delatola等提出了一種基于貝葉斯分析方法的半參數SV模型（SPM），并通過數值模擬驗證了該模型較傳統SV類模型的優越性，該類完全放棄對觀測方程的隨機誤差項的參數假設，考慮一個半參數的SV模型，在這種模型中，收益的分布是非參數化的，相比于參數分布能夠更好地描述金融資產收益特性，并能夠提高收益和風險價值的預測精度。

本文的主要貢獻是首次嘗試在半參數隨機波動（Semiparametric Stochastic Volatility，SPM）模型框架內來考察世界黃金價格波動過程的動態特征。選取2003年1月1日至2017年8月10日期間世界黃金期貨市場收盤價為原始數據，利用SPM、SV-N、SV-T模型進行實證研究，使用MCMC方法進行參數估計，以期能夠較為精確地掌握世界黃金期貨市場的波動特征。

二、模型及MCMC估計方法

（一）SV-N模型

Taylor等提出了SV模型，SV類模型在波動過程中引入了一個新的隨機過程，相較于GARCH族模型，其對收益率的擬合能力更強，且對波動率具有更好的擬合效果和預測能力。

標準的SV模型如下：

yt=exp（ht/2）εt，εt～i，i，dN（0，1），t= 1，2，…，n（1）

其中，ht表示第t日的收益率的對數波動率，而yt則代表第t日的收益率，誤差項εt和ηt相互獨立，ηt為波動的擾動水平，獨立同分布于正態分布，εt獨立同分布N（0，1）。φ為持續性參數，反映的是當前波動對未來波動的持續影響，當|？覬|<1，SV是協方差平穩的。

（二）SV-T模型

因為多數金融時間序列的無條件分布與標準正態分布相比，會呈現出尖峰厚尾的特征，這就導致SV-N模型對于描述金融時間序列有一定的局限性。許多學者嘗試對SV模型進行改進，Chib等對標準SV模型中觀測方程的隨機誤差項設定為具有厚尾特征的分布如t分布、GED 分布等，Liesenfeld R and Jung RC提出了SV-T模型，并發現該模型可以更好的刻畫金融數據尖峰厚尾分布特征。

SV-T模型如下：

yt=exp（ht/2）εt，εt～i，i，dt（0，1，v），t= 1，2，…，n（2）

ht+1=u+φ（ht-u）+ηt，ηt～i，i，dN（0，δη），t= 1，2，…，n

f（εt）=[（v-2）]■■1+■■

與標準SV模型最主要的區別在于SV-T中令誤差項，并以此來刻畫厚尾特征。（2）中第三個式子是用來描述金融數據“尖峰厚尾”特征的，當4

（三）SPM模型

Kim等提出線性標準SV模型，定義rt=logy■■和εt=logv■■，結果如下：

rt=ht+εt，εt～F，

ht+1=μ+？覬（ht-μ）+σηt，ηt～N（0，1）（3）

如果vt服從正態分布，可以看到εt服從logχ■■分布，Kim等提出通過仔細調整的有限正態混合分布去近似logχ■■的分布，Delatola等提出對于不知εt～F的分布，利用Dirichlet過程先驗這一非參數分布對εt進行統計建模，使用一個無限正態混合分布去近似εt的分布。即

εt|μ■～N（μ■，βσ■■）μ■～G，G～DP（α，G■）G■≡N（μ■，（1-β）σ■■）

其中，DP表示Dirichlet過程；α和G0分別表示精度參數和基分布；β為光滑參數。用非參數混合Dirichlet過程表示εt的條件分布為無限個均值不同，方差相同的正態分布混合分布，條件均值μt服從精度參數為α的Dirichlet過程，且基分布的均值為μ0，方差為（1-β）σ■■的正態分布。

另外，由于Kim等對數據轉換為線性模型的時候發現了一個問題，即當收益率的值很接近于零或等于零時，這就使得收益率數據變換后的值是極小的負值甚至為負無窮，因此，Kim等參照Fuller的做法，引入一個比較小的補償參數c，于是rt=log（y■■+c），相應地這里也要對εt的分布進行修改，即

p（εt）=WN（logc，σc）+（1-W）■ωjN（μj，βσ■■）

其中W表示為收益率為零的概率。如果模型不做這樣的修改，那么由于零收益率的存在，這使得模型的MCMC抽樣不容易收斂。此外，如果εt服從一個參數分布，則其均值是固定的，因此在波動率方程中均值μ是可識別的。但是此模型中εt有一個非參數先驗分布，于是εt的均值是隨機的，參照Bush等的做法將μ加入到εt中，因此模型（3）重新表示成如下形式（SPM）：

rt=h■■+ε■■，ε■■～F，

h■■=？覬h■■+σηt，ηt～N（0，1）

其中ε■■=εt+μ，h■■=ht-μ，以此將μ與εt區分開來。在SPM模型中，收益的分布是非參數化的，相比于參數分布能夠更好地描述金融資產收益特性，并能夠提高收益和風險價值的預測精度。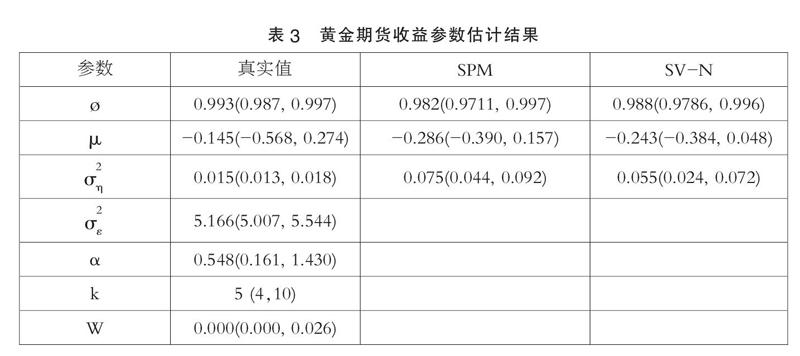

（四）MCMC估計方法

由于模型中包含不可觀測的變量——波動率，所以模型的參數估計比較困難。這里簡單介紹SPM模型的MCMC估計參數方法，具體參照Delatola等設計的MCMC抽樣方法。令y*=（y■■，y■■，…，y■■），h=（h1，h2，…，hn）andμ′=（μ1′，μ2′，…，μn′），指示變量S=（S1，S2，…，Sn）用來判斷Dirichlet過程特殊值屬于哪種混合分布。MCMC算法更新參數步驟如下：

1. 設定？覬，σ■■，σ■■，μ0，μ′，M，S和W的初值；

2. 從后驗分布h|y*，？覬，σ■■，σ■■，μ0，μ′，M，W，S中更新h；

3. 從后驗分布S|y*，？覬，σ■■，σ■■，μ0，μ′，M，W，H中更新s；

4. 從后驗分布σ■■，μ0，μ′，M，W|y*，？覬，σ■■，S，h中更新σ■■；

5. 從后驗分布？覬，σ■■|y*，σ■■，μ0，μ′，M，W，S，h中更新？覬。

三、黃金市場的實證分析

（一）數據說明與統計描述

本文選取2003年1月1日至2017年8月10日共3723組世界黃金期貨市場收盤價為樣本數據（如圖1所示），數據來源于 Investing.com。在實證分析中將日收盤價轉換為日收益率來使用，收益率采用JP摩根集團的對數收益率的概念，即Rt=lnpt-lnpt-1（其中Rt是收益率，pt是第t日的黃金期貨收盤價，pt-1是前一日的黃金期貨收盤價）。

（a）給出了黃金期貨日度收盤價格的變化軌跡，可以看出在2012年以前黃金價格一度走高，說明在黃金期貨市場開放以來，越來越多的投資者與機構意識到了黃金期貨增值、規避風險等特性；而從（b）可以看到黃金期貨收益率具有金融數據所特有的波動聚集性，暴漲暴跌這種極端情況比比皆是；從（c）、（d）兩圖我們可以看到無論是經驗收益率密度還是QQ圖，均與正態分布偏離較大，說明黃金期貨收益率序列并不服從正態分布。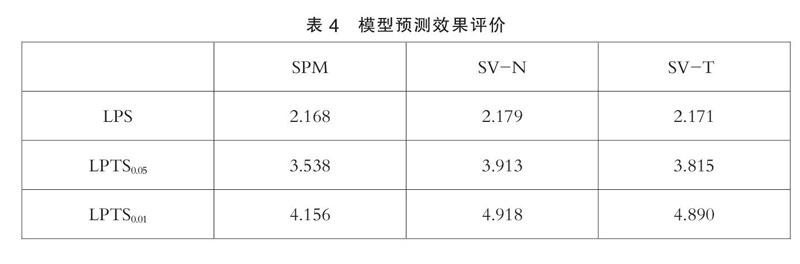

從表1中可以看到黃金期貨對數收益率序列偏度為-0.3748936（左偏），峰度為 8.043399（高峰），說明該序列具有金融數據所特有的“尖峰厚尾”性。JB 檢驗P 值<0.01，即JB 檢驗值位于拒絕域內，ADF=-15.273，小于ADF檢驗1%～10%的各種顯著水平ADF臨界值，又p=0.01，所以拒絕原假設（原假設為非平穩），即認為黃金期貨日收益率序列是平穩的。綜上描述，可以應用SV-N、SV-T及SPM模型對黃金期貨日收益率序列進行實證研究。

（二）參數估計與黃金期貨實證研究

根據SPM模型模擬產生樣本長度的觀測序列，其中？覬0=0.97，σ2=0.15，εt服從7個正態分布的混合分布。運用MCMC抽樣方法進行參數估計，得到模型參數估計結果。

表2給出了數值模擬的實驗結果，參數估計結果和相應的95%的置信區間，參數估計的結果接近于相應的真實值，且真實值均處于置信區間中，表明此估計方法比較準確，可以獲得合理并有效的參數估計結果。本文以黃金期貨日度收益率數據，運用MCMC抽樣方法估計參數，運行100000次抽樣，前5000次作為預熱舍棄，后95000次抽樣值用于模型分析，得到模型參數估計結果如表4所示。

表3給出了SPM模型、SV-N模型和SV-T模型的參數估計結果。從表中可以看出，波動率持續性參數 的估計值均接近于1，這意味著黃金期貨收益的波動過程明顯具有很強的持續性，其中SPM模型的值最大，證明了SPM模型能夠更好地刻畫序列的波動持續性。參數估計值大于4，說明分布具有厚尾特征。

（三）模型比較

本文采用對數預測得分對模型預測效果進行比較研究，向前一步預測的平均定義為：

LPS=■■logp（r■|r■）

其中rt=（r1，r2，…，rt）。一般LPS值越小說明模型預測能力越好，但研究發現，通常不同模型LPS值比較接近，另外在金融風險管理領域中，人們更關注于極端事件，因此對極端事件的預測能力更重要，于是本文采用對數預測尾部得分（LPTSβ）對模型極端風險預測效果進行比較研究LPTSβ定義分別為：

LPTSβ=■∑■■I（ri>zβ）logp（r■|r■）

其中zβ表示收益數據經驗分布的上100β%分位數。具體評價準則為LPTSβ值越小，說明模型對于極端事件預測能力越好。

表3給出黃金期貨日度收益率數據在不同模型中預測結果，從表4可以看出不同模型的LPS得分值非常接近，說明模型預測能力均較好，但是在LPTS得分，SPM模型得分值最小，說明在極端風險預測方面上，SPM模型預測效果最好。因此，SPM模型不但能夠較好刻畫黃金期貨日度收益率數據，而且對極端事件預測方面均有較好的效果。

四、結語

本文使用SV-N、SV-T、SPM模型和MCMC估計方法對世界黃金價格波動過程的動態特征進行了實證分析，采用對數預測得分對模型預測效果進行比較研究。結果表明，從LPTS得分看，SPM得分最低，預測效果最好。相較于SV-N、SV-T模型，SPM在刻畫金融數據尾部特征以及波動特征方面能力更強、擬合效果更好。

參考文獻：

[1]陳楊林，向東進.基于波動率模型的世界黃金價格實證分析[J].決策與信息：財經觀察，2008（09）.

[2]Batten J A， Lucey B M. Volatility in the Gold Futures Market[C].IIIS，2007.

[3]王兆才.上海黃金期貨收益率波動狀態轉換行為研究——基于MCMC參數估計的MRS-GARCH（1，1）模型[J].世界經濟情況，2012（01）.

[4]孫趙暉.中國黃金市場波動性特征分析[J].長沙理工大學學報（社會科學版）， 2015（02）.

[5]劉雪潔.中國黃金期貨市場波動特征和風險度量研究[D].首都經濟貿易大學，2016.

[6]蘇理云，王杰.基于SV-POT模型的黃金市場的動態VaR預測[J].重慶理工大學學報，2017（05）.

[7]Delatola E I， Griffin J E. Bayesian Nonparametric Modelling of the Return Distribution with Stochastic Volatility[J]. Social Science Electronic Publishing， 2011（04）.

[8]Mark J. Jensen and John M. Maheu. Bayesian Semiparametric Stochastic Volatility Modeling[J]. Journal of Econometrics，20

10（02）.

[9]Taylor S J. Financial returns modelled by the product of two stochastic processes | a study of daily sugar prices 1961-79[J]. Time，2005（01）.

[10]Chib S， Shephard N， Nardari F. Markov Chain Monte Carlo Methods for Generalized Stochastic Volatility Models[J]. Economics，1998（08）.

[11]Liesenfeld R， Jung R C. Stochastic volatility models： conditional normality versus heavy-tailed distributions[J]. Journal of Applied Econometrics，2000（02）.

[12]Bush C A， Maceachern S N. A Semiparametric Bayesian Model for Randomised Block Designs[J]. Biometrika，1996（02）.

[13]Durham G B. SV mixture models with application to S&P; 500 index returns[J]. Journal of Financial Economics，2007（03）.

[14]Jacquier E，Polson N G，Rossi P E， Bayesian analysis of stochastic volatility models[J]. Journal of Business &Economic; Statistics，2002（01）.

[15]Broto， C. and Ruiz， E. Estimation methods for stochastic volatility models： a survey[J]. Journal of Economic Surveys， 2004（18）.

[16]江良，林鴻熙.隨機波動率Hull-White模型參數估計方法[J].系統工程學報，2016（05）.

[17]Chib S， Shephard N， Nardari F. Markov Chain Monte Carlo Methods for Generalized Stochastic Volatility Models[J]. Economics，1998（08）.

[18]Durham G B. SV mixture models with application to S&P; 500 index returns[J]. Journal of Financial Economics， 2007 （03）.

[19]Mark J. Jensen and John M. Maheu. Bayesian Semiparametric Stochastic Volatility Modeling[J]. Journal of Econometrics，2010（02）.

[20]Christie A A.The stochastic behavior of common stock variances[J]. Journal of Financial Economics，1982（10）.

[21]Kim S， Shephard N， Chib S. Stochastic volatility： likelihood inference and comparison with ARCH models[J]. The review of economic studies，1998（03）.

（作者單位：貴州大學數學與統計學院）