五種彈性配準方法在放射治療CT圖像配準中的應用比較

龐皓文 孫小楊 楊 波

在臨床放射治療過程中，由于患者體重變化、腫瘤退縮以及危及器官分次狀態不同，導致腫瘤靶區與危及器官吸收劑量與初始放射治療計劃產生較大不同，通過重新掃描CT圖像以及重新制作放射治療計劃，減少上述變化帶來的影響，并監測放射治療過程中腫瘤與危及器官的變化，以及帶來的劑量影響，而實現患者的自適應放射治療是腫瘤放射治療研究的熱點[1-5]。

彈性配準算法通過比較不同分次放射治療時患者CT圖像，了解腫瘤與危機器官的形變過程，進一步計算出放射治療全過程中腫瘤與危機器官的累加劑量，是自適應放射治療的理論基礎，同時加入時間因素的四維放射治療也建立在彈性配準基礎上[6-7]。Mencarelli等[8]和Francisco等[9]通過研究形變配準算法模型模擬腫瘤與危及器官在放射治療過程中變化的不確定性，探索了彈性配準在放射治療中的應用，而在放射治療中應用彈性配準算法，需要建立準確、快速與自動的軟件平臺。為此，本研究通過自主編程的軟件平臺，對Horn-Schunck光流法、Demons算法、加速Demons算法、水平集算法以及快速自由形變算法5種常見的彈性配準方法在盆腔放射治療患者CT圖像中的配準精度進行比較。

1 CT圖像配準設備與方法

1.1 設備與原理

(1)設備。使用LightSpeed Plus 4型CT(美國GE公司)。

(2)原理。5種常見的彈性配準方法有Horn-Schunck光流法[10]、Demons算法[11]、加速Demons算法[12]、水平集算法[13]以及快速自由形變算法[14]。

設定兩組圖像，一組為待配準圖像灰度值為M(v)；一組為參考圖像灰度值為S(v)，v為三維空間的方向。彈性配準是通過找出待配準圖像形變為參考圖像合適的位移場u(v)，使得其灰度值從M(v)改變為M(v-u)后，與參考圖像的灰度值S(v)類似，用于測量相似度的函數計算為公式1：

圖像彈性形變的過程是搜尋位移場u(v)的過程，不同的彈性配準方法u(v)的取值各有差異。

1.2 Horn-Schunck光流法

Horn-Schunck光流算法u(v)實現迭代為公式2：

式中u為鄰域均值；λ為權重值；n為迭代次數。

1.3 Demons算法

Demons算法u(v)實現迭代為公式3：

式中Gσ為高斯低通濾波函數，窗寬為σ；n為迭代次數。

1.4 加速Demons算法

加速Demons算法u(v)實現迭代為公式4：

式中Gσ同Demons算法；n為迭代次數。

1.5 水平集算法

水平集算法u(v)實現迭代為公式5：

式中u(v)ninit=(M(v)-S(v)),Gσ同Demons算法，n為迭代次數。

1.6 快速自由形變算法

快速自由形變算法u(v)實現迭代為公式6：

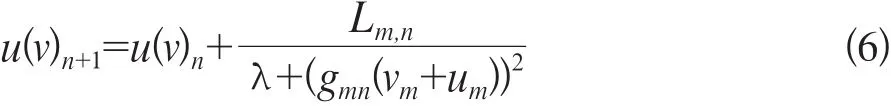
式中Lm,n= λΔ2(um,n)-[M(vm+um)-S(vm)]gm,n(vm+um),g(v)=ΔM(v)， n為迭代次數。

1.7 彈性配準迭代步驟

(1)初始時，n=0，u(v)0=0。

(2)設n=n+1，選取公式(2～6)中一種對位移場u(v)n+1實現迭代，待配準圖像迭代為Mn(v-u(v)n+1)。

(3)判別迭代次數小于預設值，轉為迭代停止[步驟(4)]，否則轉為步驟(2)。

(4)迭代停止，Mn(v-u(v)n+1)為最后待配準圖像，彈性配準中選用多分辨策略。

2 CT圖像配準結果

2.1 試驗對比參數

使用Matlab 2016 a軟件，根據上述5種常見的彈性配準算法原理，編寫具有完全知識產權代碼的彈性配準程序，并對10例行盆腔放射治療患者的定位時與放射治療中兩組CT圖像執行彈性配準。其中放射治療定位時CT圖像為參考圖像、放射治療中CT圖像為待配準圖像，比較五種常見的彈性配準方法的配準精度。硬件為英特爾酷睿i5-3210 M CPU，2.5 GHz，4 G內存。10例行盆腔放射治療患者CT斷層圖像分辨率為512×512，層厚為5 mm。10例患者均方誤差(mean squared error，MSE)、平均相關系數(correlation coefficient，CC)及平均配準用時見表1。

表1 五種算法評價參數及用時

2.2 平均MSE

Horn-Schunck光流法平均MSE減少26.0%，Demons算法平均MSE減少18.5%，快速Demons算法平均MSE減少6.7%，水平集算法平均MSE減少22.7%，快速自由形變算法平均MSE減少13.4%。

2.3 平均CC

Horn-Schunck光流法平均CC提高3.7%，Demons算法平均CC提高3.3%，快速Demons算法平均CC提高2.4%，水平集算法平均CC提高3.4%，快速自由形變算法平均CC提高2.6%；均配準時間為107.5～220.8 s。

2.4 配準后的CT冠狀面差分圖

為了更全面了解配準前后放射治療CT圖像的差別，選取本研究中第5例盆腔放射治療患者為例，其基于5種常用的彈性配準算法配準后的CT冠狀面差分圖如圖1所示。

圖1 五種常用彈性配準算法配準后的CT冠狀面差分圖

3 結論

評價參數表明，本研究中的5種常用的彈性配準算法均取得了較好的配準結果，其中Horn-Schunck光流法平均MSE減少26.0%、CC提高3.7%，其配準平均耗時也最少，因此推薦使用Horn-Schunck光流法對放射治療CT圖像進行配準。全部放射治療過程中腫瘤及危及器官持續變化，將彈性配準方法應用于放射治療圖像配準中，可進一步了解腫瘤及危及器官的變化帶來的劑量學變化。但現階段的彈性配準理論并不能真實模擬腫瘤及危及器官的實際變化，故下一步研究擬開發出應用于放射治療的具有自主知識產權和代碼的醫學圖像彈性配準軟件平臺，通過在腫瘤或危及器官中植入標記點的方法，總結最真實模擬各個腫瘤及危及器官的變化模型，并將其轉化為適合各個腫瘤及危及器官個體化的彈性配準數學模型，進一步提高配準精度，對放射治療中腫瘤及危及器官的變化進行評估，實現放射治療全程中腫瘤及危及器官的個體化劑量監測[15-18]。

[1]Yan D，Jaffray DA，Wong JW.A model to accumulate fractionated dose in a deforming organ[J].Int J Radiat Oncol Biol Phys，1999，44(3)：665-675.

[2]Noel CE，Santanam L，Olsen JR，et al.An automated method for adaptive radiation therapy for prostate cancer patients using continuous fiducial-based tracking[J].Phys Med Biol，2010，55(1)：65-82.

[3]Qi XS，Santhanam A，Neylon J，et al.Near Real-Time Assessment of Anatomic and Dosimetric Variations for Head and Neck Radiation Therapy via Graphics Processing Unit-based Dose Deformation Framework[J].Int J Radiat Oncol Biol Phys，2015，92(2)：415-422.

[4]Swaminath A，Massey C，Brierley JD，et al.Accumulated Delivered Dose Response of Stereotactic Body Radiation Therapy for Liver Metastases[J].Int J Radiat Oncol Biol Phys，2015，93(3)：639-648.

[5]Teo BK，Bonner Millar LP，Ding X，et al.Assessment of cumulative external beam and intracavitary brachytherapy organ doses in gynecologic cancers using deformable dose summation[J].Radiother Oncol，2015，115(2)：195-202.[6]Velec M，Moseley JL，Craig T，et al.Accumulated dose in liver stereotactic body radiotherapy：positioning，breathing，and deformation effects[J].Int J Radiat Oncol Biol Phys，2012，83(4)：1132-1140.

[7]Chan MK，Kwong DL，Ng SC，et al.Experimental evaluations of the accuracy of 3D and 4D planning in robotic tracking stereotactic body radiotherapy for lung cancers[J].Med Phys，2013，40(4)：041712.

[8]Mencarelli A，van Kranen SR，Hamming-Vrieze O，et al.Deformable image registration for adaptive radiation therapy of head and neck cancer：accuracy and precision in the presence of tumor changes[J].Int J Radiat Oncol Biol Phys，2014，90(3)：680-687.

[9]Salguero FJ，Saleh-Sayah NK，Yan C，et al.Estimation of three dimensional intrinsic dosimetric uncertainties resulting from using deformable image registration for dose mappi ng[J].Med Phys，2011，38(1)：343-353.

[10]Horn B，Schunck B.Determining optic flow[J].International Journal of Artificial Intelligen ce，1981，17(2)：185-203.

[11]Thirion JP.Image matching as a diffusion process： an analogy with Maxwell's demons[J].Med Image Anal，1998，2(3)：243-260.

[12]Wang H，Dong L，O'Daniel J，et al.Validation of an accelerated'demons' algorithm for deformable image registration in radiation therapy[J].Phys Med Biol，2005，50(12)：2887-2905.

[13]Vemuri BC，Ye J，Chen Y，et al.Image registration via level-set motion：applications to atlas-based segmentation[J].Med Image Anal，2003，7(1)：1-20.

[14]Lu W，Chen ML，Olivera GH，et al.Fast free-form deformable registration via calculus of variations[J].Phys Med Biol，2004，49(14)：3067-3087.

[15]Jin P，van der Horst A，de Jong R，et al.Markerbased quantification of interfractional tumor position variation and the use of markers for setup verification in radiation therapy for esophageal cancer[J].Radiother Oncol，2015，117(3)：412-418.

[16]Bolton WD，Richey J，Ben-Or S，et al.Electromagnetic Navigational Bronchoscopy：A Safe and Effective Method for Fiducial Marker Placement in Lung Cancer Patients[J].Am Surg.2015，81(7)：659-662.

[17]Langerak T，Mens JW，Quint S，et al.Cervix motion in 50 cervical cancer patients assessed by daily cone beam computed tomographic imaging of a new type of marker[J].Int J Radiat Oncol Biol Phys，2015，93(3)：532-539.

[18]Takao S，Miyamoto N，Matsuura T，et al.Intrafractional baseline shift or drift of lung tumor motion during gated radiation therapy with a real-time tumor-tracking system[J].Int J Radiat Oncol Biol Phys，2016，94(1)：172-180.