從高考數學的解析幾何題中看教學中歸納總結的重要性

廣東省深圳市寶安中學（集團）高中部 王延偉

2010年廣東省高考的20題：

（2）若過點 的兩條直線l1和l2與軌跡E都只有一個交點，且，求h的值。

本題（2）所涉及的問題思路很簡單,但有很麻煩的計算，很多學生知道怎么計算，可算不出最后的結果。其實要做好本題的關鍵是將直線方程代入橢圓方程后計算判別式問題，學生感覺計算困難是由于我們平時教學時，對直線與圓錐曲線相交問題的研究分析不夠，沒有去分析判別式等與直線的斜率、縱截距、圓錐曲線中的交點的關系。

筆者從自己的教學中總結如下規律：

直線與圓錐曲線相交問題中常用到的方程和判別式化簡后的結果：

將直線代入曲線方程后得：

只要觀察上面兩個方程就不難看出判別式與上面兩個方程的關系。

規律：判別式中，m，n就是方程（1）中兩個分母中的系數，而是方程（2）的x二次項的系數，即為二次項的系數減去直線方程中縱截距的平方。

2.特殊地：

①判別式化簡規律：

③相交弦AB的中點坐標（x0，y0）的規律：

①判別式化簡規律：

③相交弦AB的中點坐標（x0，y0）的規律：

①判別式化簡規律：

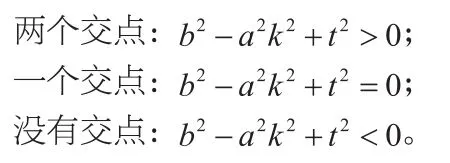
③相交弦AB的中點坐標（x0，y0）的規律：

①判別式化簡規律：

③相交弦AB的中點坐標（x0，y0）的規律：

如果在教學中多總結一些規律性的東西，不僅能幫助學生提高分析問題的能力，同時也能使學生很快計算出結果，由此看出，教學中總結規律非常重要。