數形結合思想方法*

●

(學軍中學，浙江 杭州 310000)

1 考點回顧

數形結合是中學階段重要的思想方法，是培養學生直觀想象能力的重要途徑，是提升學生核心素養的重要載體.從數到形，由形到數，讓學生在分析問題和解決問題中提升素養.從數到形，問題更加直觀；由形到數，問題更加嚴謹，更加貼近數學的本質.

數形結合思想是浙江省數學高考重點考查的內容之一.浙江省試題具有簡潔嚴謹的特點，非常注重學生對問題本身的理解，對數形結合思想的考查常從概念出發，形成圖形，然后解決問題.如2017年浙江省數學高考試題第3～5,7,10,15,17,21題，都與數形結合有關，可以預測：數形結合思想仍將是2018年浙江省數學高考考查的重點和熱點之一.

2 典題剖析

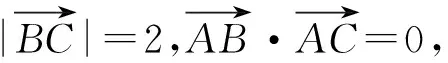
分析如圖1，點A在以O為圓心、BC為直徑的圓上，由已知條件得

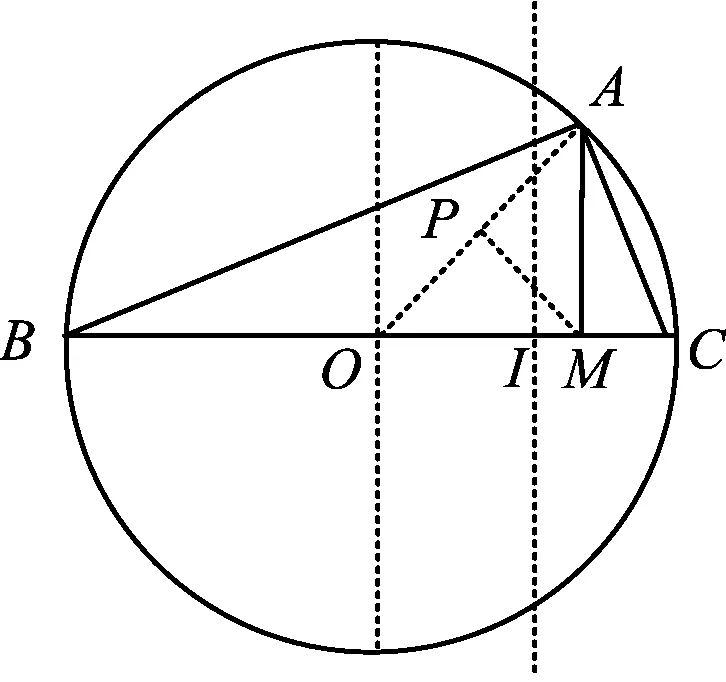
圖1

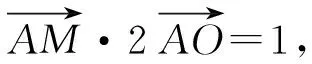
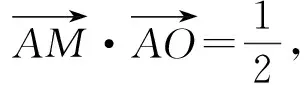
從而

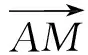
評注本題關鍵在于形的構造，找到點M動的原因是點A在圓上運動，由此將問題轉化為對投影的分析，通過尋找兩個極端位置，順利實現對本題的突破.

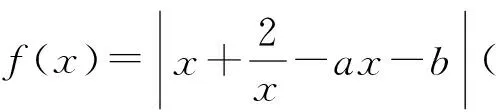
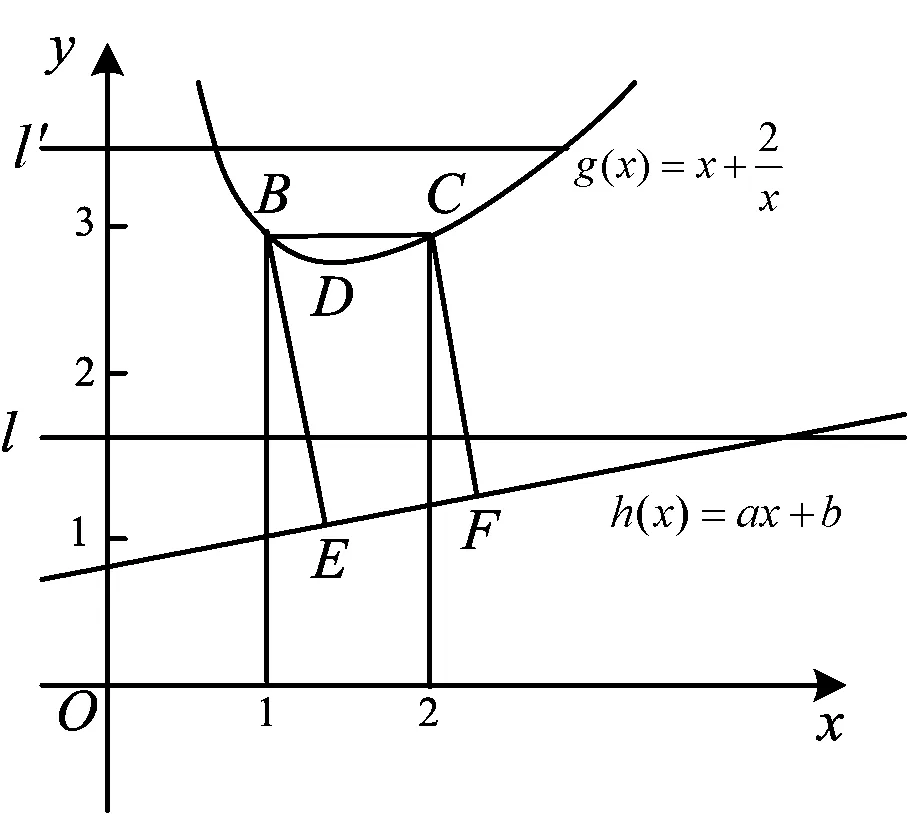
圖2

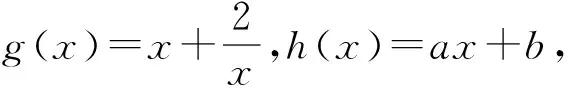
評注本題關鍵在于對絕對值的分析，轉化為兩個函數縱向距離差的最大值，逐步分析，最終找到取到復合最小值的位置.

例3若不等式(ax+3)(x2-b)≤0對任意的x∈(0,+∞)恒成立，則 ( )

A.ab2=9 B.a2b=9,a<0

C.b=9a2,a<0 D.b2=9a

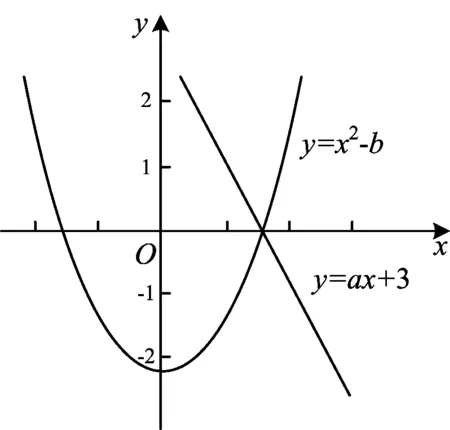
圖3

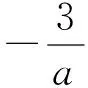
評注從兩個函數的圖形特點出發，分析兩個函數零點必有一個重合的條件，本題通過一個圖，巧妙地回避了很多討論，非常靈巧.

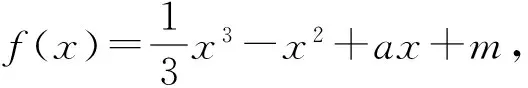
A．必為正數 B．必為負數

C．必為非負 D．必為非正

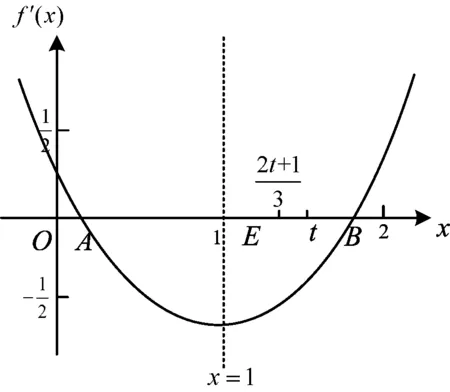
圖4

分析由題意知f′(x)=x2-2x+a，設A,B為f′(x)的兩個零點，則

f′(t+2)>0.

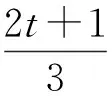
評注本題的數形結合一氣呵成，從中發現點E是1～t之間的三等分點，這是本題最大的亮點，充分說明圖形是解決問題的重要載體.

例5設函數f(x)=x2-ax+a+3，g(x)=ax-2a，存在x0∈R，使得f(x0)≤0與g(x0)≤0同時成立，求實數a的最小值.

分析對a進行討論：

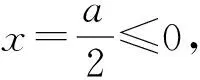
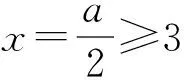
綜上所述，a的最小值為7.

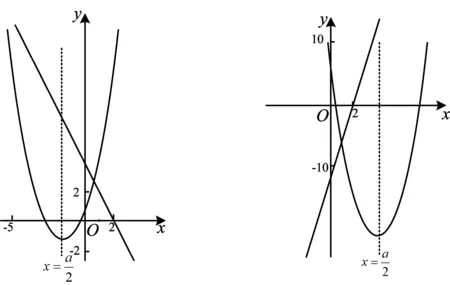
圖5 圖6

評注問題的關鍵在于對于同一個x0，函數值均不大于0，反映在圖像上均小于0，這個關鍵在于排除a≤0的情況，然后找到a>0情形的邊界條件.

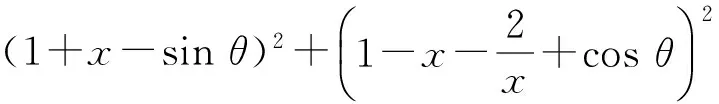
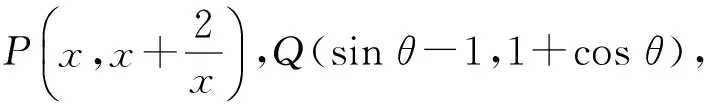
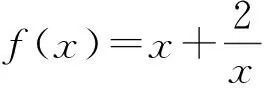
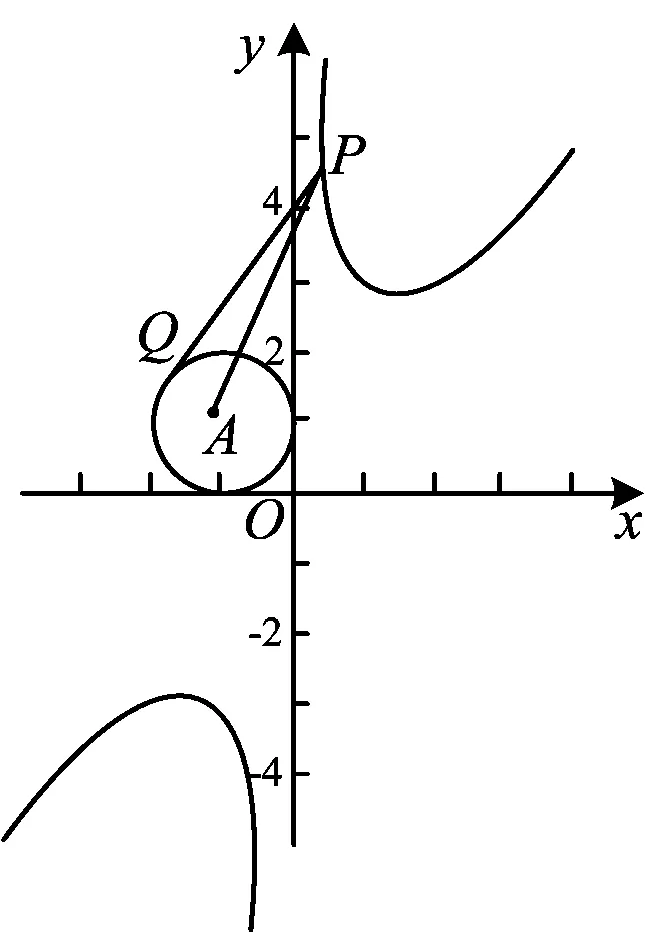
圖7

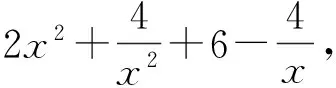
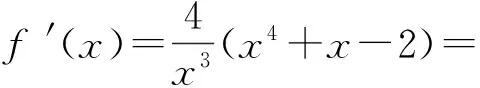
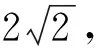
評注把代數問題轉化為距離問題，把兩個動點距離問題轉化為圓到打勾函數的距離問題.這是本題的亮點，也是數形結合的重要運用.本題通過圖形發現問題、分析問題，然后解決問題.

3 精題集萃

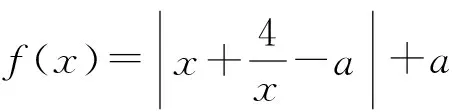
2.已知向量a,b滿足|a|=1，|b|=2，則|a+b|+|a-b|的最大值是______，最小值是______.

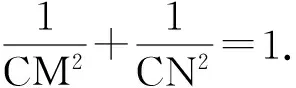
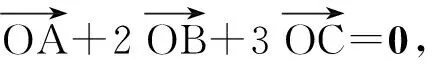
參考答案

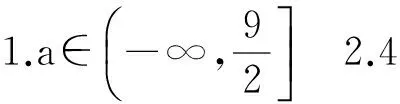
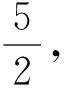
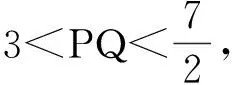
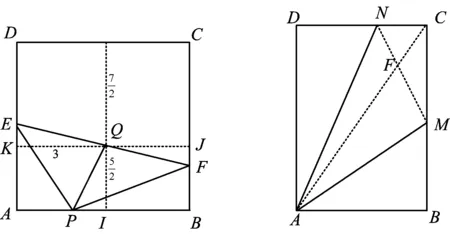
圖8 圖9

7.解如圖9，聯結AC,MN交于點F.由點N,F,M共線可知

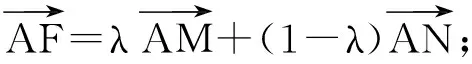
由點A,F,C共線可知

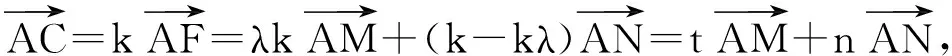
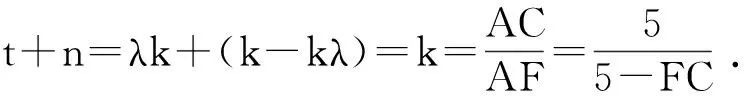
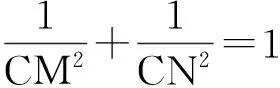
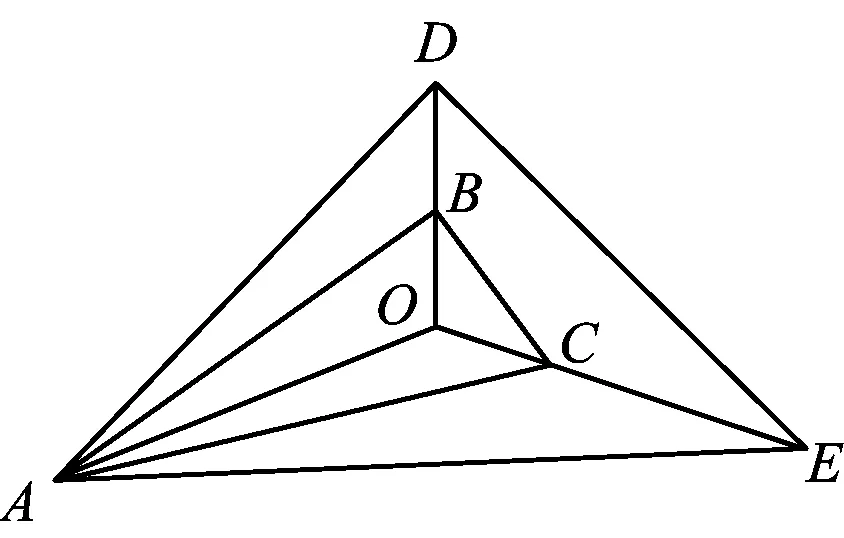
圖10

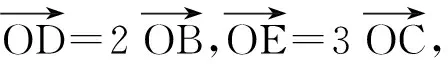
[1] 范迪飛,朱哲．以“本”為據 以“思”促教——高三數學解題教學的實踐與思考[J]．中學教研(數學)，2017(12)：9-12.

[2] 張春杰．數形結合思想方法[J]．中學教研(數學)，2017(2)：23-26.