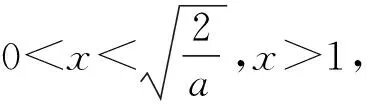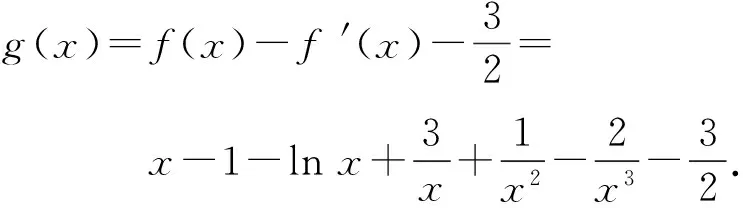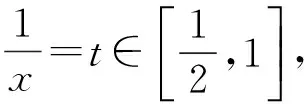函數與導數復習專題*

●

(平湖中學,浙江 平湖 314200)

1 考點回顧

函數是高中數學的重要內容，是描述客觀世界變化規律的重要數學模型，貫穿了整個高中階段的數學學習，是高考數學中突出考查的主干知識，在歷年浙江省數學高考中都占非常大的比重.導數及其應用深化和提高了函數的學習和研究.

函數的考查內容包括：函數的概念與函數的表示方法；函數的單調性、奇偶性、最值等；基本初等函數——指數函數、對數函數、冪函數；函數與方程的關系；函數的簡單應用.導數通常考查3個方面：導數的幾何意義；利用導數研究函數的單調性、函數的極值或最值；用導數證明不等式問題及方程等.在數學思想方法上突出考查學生應用函數與方程思想、數形結合思想、分類討論思想以及轉化與化歸思想的能力；在數學能力方面關注學生的運算求解能力、推理論證能力、抽象概括能力，以及知識遷移到新問題中思考并靈活解決新問題的綜合能力，重視學生用數學的眼光觀察問題、用數學的思維分析問題、用數學的語言表達問題的綜合素養的考查，檢測學生個體理性思維的廣度和深度，以及進一步學習的潛能.

2 典例剖析

2.1 函數的概念及性質

例1存在函數f(x)滿足：對任意x∈R,都有 ( )

A.f(sin 2x)=sinxB.f(sin 2x)=x2+x

C.f(x2+1)=|x+1| D.f(x2+x)=|x+1|

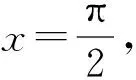
分析2利用函數周期性和對稱性.對于選項A，令t=sin 2x,則t的最小正周期是π，而y=sinx的最小正周期是2π，兩者矛盾；對于選項B，令t=sin 2x，則t的最小正周期是π，而y=x2+x不是周期函數，兩者矛盾；對于選項C，令t=x2+1，則t關于x的二次函數的對稱軸為x=0，而y=|x+1|的對稱軸為x=-1，兩者矛盾.故選D.

評注本題主要考查函數的概念，及對函數概念的深入理解，包括函數的定義域、值域、周期性等，這些是研究函數的重要依據和載體.

2.2 函數的圖像與函數的零點

例2已知函數

其中m>0，若存在實數b，使得關于x的方程f(x)=b有3個不同的根，則m的取值范圍是______(答案：(3,+∞)).

分析當x>m時，f(x)=x2-2mx+4m=(x-m)2+4m-m2，其頂點為(m,4m-m2)；

當x≤m時，函數f(x)的圖像與直線x=m的交點為Q(m,m).

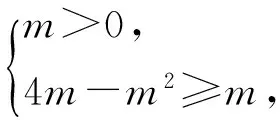
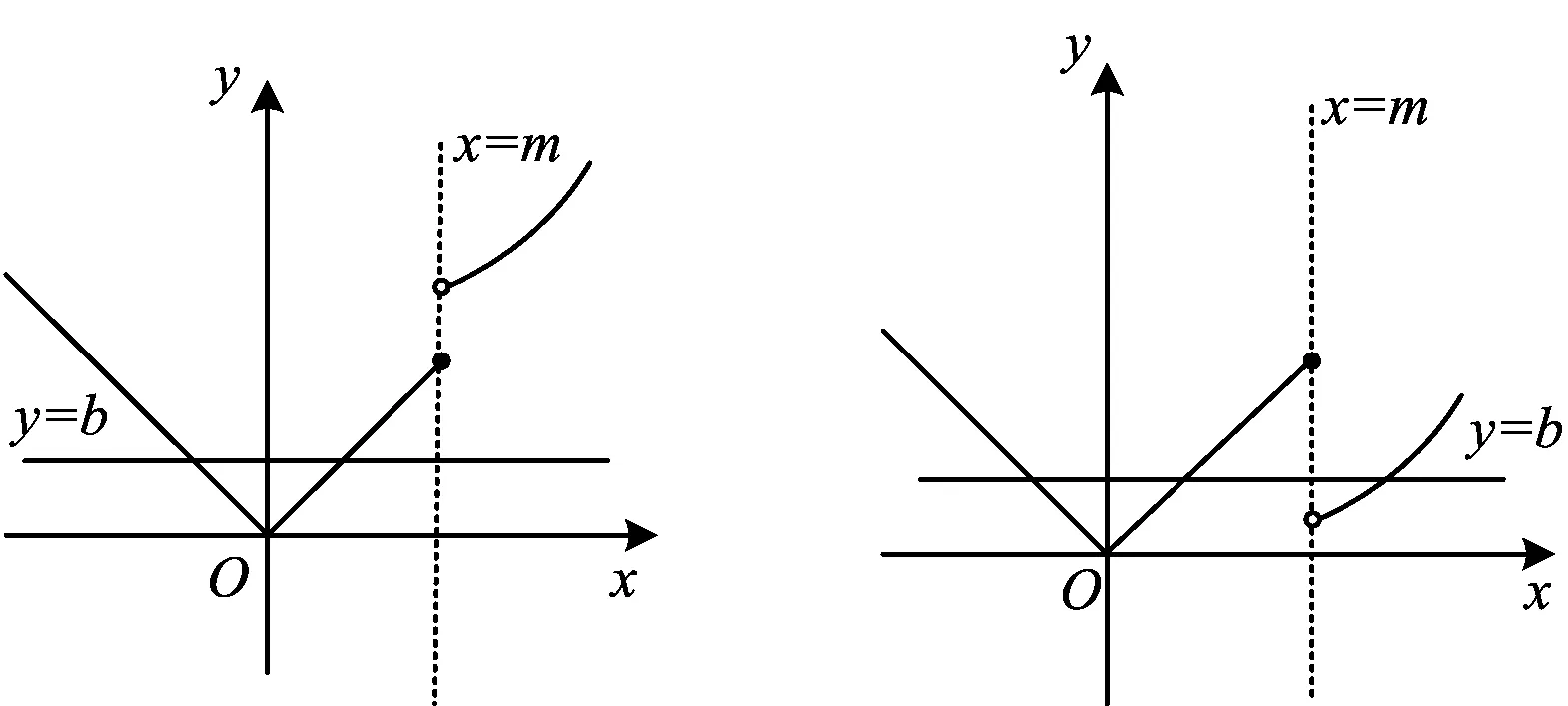
圖1 圖2

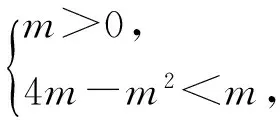
綜上所述，m的取值范圍為(3,+∞)．

評注1)函數零點常與導數知識結合用于判斷函數存在唯一零點等命題．解題時常先判斷函數在某區間上存在零點(存在性)，再說明函數在相應區間上單調遞增(或單調遞減)即可(唯一性)．

2)當題目不是求零點，而是利用零點的個數，或由零點求參數的范圍時，一般采用數形結合法．

3)研究方程f(x)=g(x)的解，實質就是研究G(x)=f(x)-g(x)的零點．

4)若函數f(x)在[a,b]上單調，且f(x)的圖像是連續不斷的一條曲線，則f(a)f(b)<0?函數f(x)在[a,b]上只有一個零點．

5)轉化思想：方程解的個數問題可轉化為兩個函數圖像交點的個數問題；已知方程有解求參數范圍問題可轉化為函數值域問題．

2.3 函數最值與參數范圍問題

例3已知函數f(x)=x-1-alnx．

1)若f(x)≥0，求a的值；

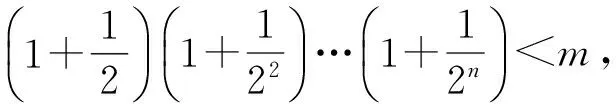
分析1)由f(1)=0知f(x)的最小值為0,對a>0和a<0這兩種情況進行分類討論，得a=1.

2)求m的最小值:一方面，當n=3時，

從而

m≥3．

另一方面，由第1)小題可得，當x>0時，

x-1-lnx≥0，

即

lnx≤x-1，

從而

ln(x+1)≤x.

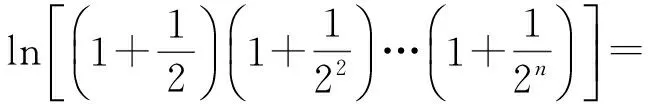
于是

因此m的最小值為3．

評注此題主要考查用導數研究函數的單調性與最值問題、放縮法研究不等式成立的條件、分類與整合思想、雙向驗證確定最值的處理方式等．第1)小題容易讓人以為是恒成立問題，疑惑為何不是求a的取值范圍，結合觀察所得特殊值f(1)=0，從而演變為最小值問題.這種設問方式有利有弊，優點在于入手更快，缺點在于過分夸大了觀察特殊值的作用.第2)小題利用第1)小題的結論獲得不等式，層層推進，拾級而上，水到渠成.

2.4 導數與函數不等式的證明

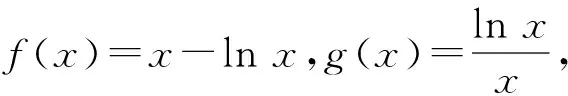
分析用直線代替曲線，引進中間函數，實現高效過渡.

從而g(x)在(0,e)上單調遞增，在(e,+∞)上單調遞減，于是

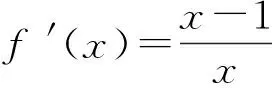
fmin(x)=f(1)=1,

因此

故

f(x)>g(x).

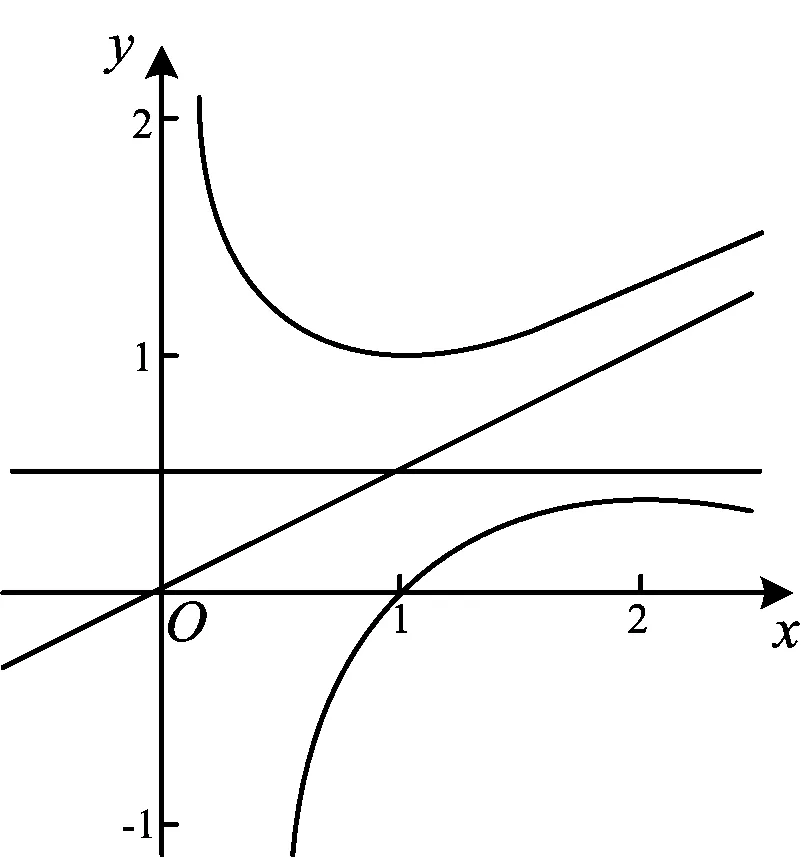
圖3

評注證明f(x)>g(x)，從形的角度來看對于任意的一個值x，都有函數y=f(x)的圖像在函數y=g(x)圖像的上方，因此，兩個函數圖像中間一定是有空隙的，可以有很多曲線可以從空隙中穿過，也可能會有直線穿過.從數的角度來理解在兩個函數中間可以尋找一個中間函數，但是最好有線性函數，對于解決問題效果更明顯.本題恰好兩個函數圖像之間可以穿越若干條直線，并且和y軸垂直的直線也有很多條，因此選擇其中一條和y軸垂直的直線作為中間過渡量(如圖3所示)，實現兩個函數的高效過渡.

3 精題集萃

1.若函數f(x)=x2+ax+b在區間[0,1]上的最大值是M，最小值是m，則M-m( )

A.與a有關，且與b有關

B.與a有關，但與b無關

C.與a無關，且與b無關

D.與a無關，但與b有關

(2017年浙江省數學高考試題第5題)

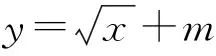
B.(0,1]∪[3,+∞)

(2017年山東省數學高考理科試題第10題)

3.若x=-2是函數f(x)=(x2+ax-1)ex-1的極值點，則f(x)的極小值為 ( )

A.-1 B.-2e-3C.5e-3D.1

(2017年全國數學高考卷Ⅱ理科試題第11題)

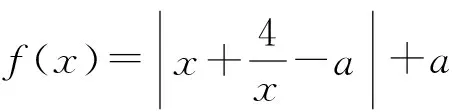
6.已知函數f(x)=ax-x2-lnx，若函數f(x)存在極值，且所有極值之和小于5+ln 2，則實數a的取值范圍是______.

7.若直線y=kx+b是曲線y=lnx+2的切線，也是曲線y=ln(x+1)的切線，則b=______.

8.已知函數f(x)=x3+ax2+bx+1(其中a>0,b∈R)有極值，且導函數f′(x)的極值點是f(x)的零點(極值點是指函數取極值時對應的自變量的值).

1)求b關于a的函數關系式，并寫出定義域；

2)證明：b2>3a；

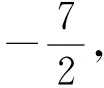
9.已知函數f(x)=-x2+2bx+c，設函數g(x)=|f(x)|在區間[-1,1]上的最大值為M．

1)若b=2，求M的值；

2)若M≥k對任意的b,c恒成立，試求k的最大值．

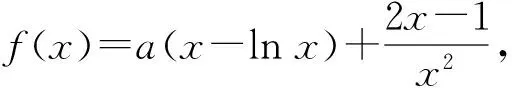
1)討論f(x)的單調性；

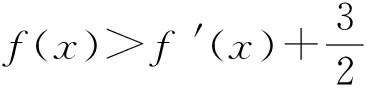
參考答案

8.1)解因為f(x)=x3+ax2+bx+1,所以

f′(x)=3x2+2ax+b.

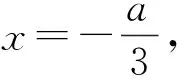
于是

又f(x)有極值，從而f′(x)=0有解，即

Δ=4a2-12b>0,

解得

a>3.

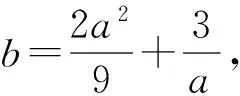
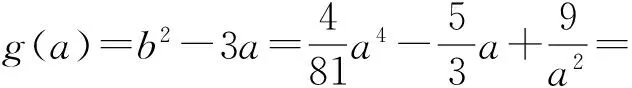
由a>3，得g(a)>0，從而b2>3a.

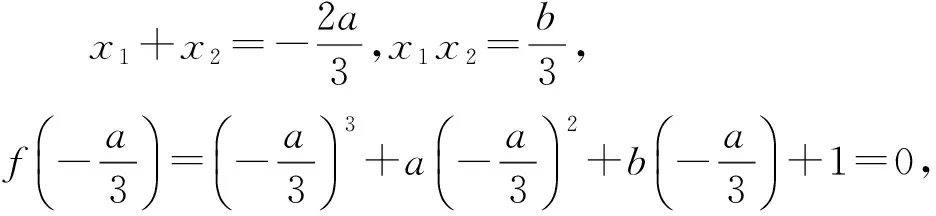
(x1+x2)3-3x1x2(x1+x2)+a(x1+

x2)2+b(x1+x2)-2ax1x2+2,

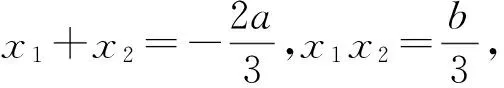
f(x1)+f(x2)=

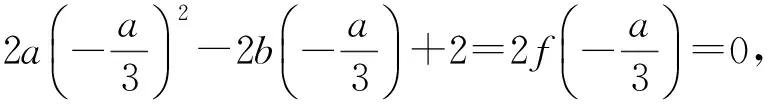
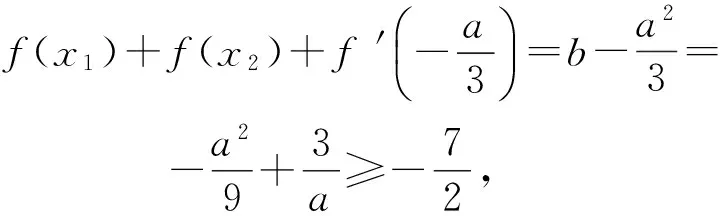
于是

2a3-63a-54≤0,

即

2a3-12a2+12a2-63a-54≤0，

故

(a-6)(2a2+12a+9)≤0.

綜上所述，a∈(3,6].

9.解1)當b=2時，f(x)在區間[-1,1]上是增函數，則

M=max{g(-1),g(1)}.

又因為g(-1)=|-5+c|,g(1)=|3+c|，所以

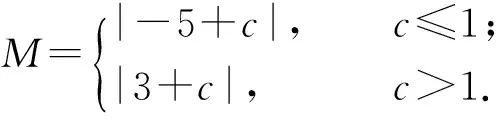
2)利用絕對值不等式.由題意得f(0)=c,f(1)=-1+2b+c,f(-1)=-1-2b+c,從而

2f(0)-[f(1)+f(-1)]=2,

即 2= |2f(0)-[f(1)+f(-1)]|≤

2|f(0)|+|f(1)|+|f(-1)|≤4M,

于是

當且僅當

10.1)解f(x)的定義域為(0,+∞)，求導得

①當a≤0時，由f′(x)>0，得01,從而f(x)的單調遞增區間為(0,1)，單調遞減區間為[1,+∞).

②當0

③當a=2時，

從而f(x)的單調遞增區間為(0,+∞).

2)證明當a=1時，

因為x∈[1,2],lnx

h(t)=-2t3+t2+3t=-t(t+1)(2t-3),

因此不等式成立.